Development of Magnetically Soft Amorphous Microwires for Technological Applications
Abstract
:1. Introduction
2. Materials and Methods
3. Magnetic Properties of as-Prepared Glass-Coated Microwires
4. Tuning of Magnetic Softness and GMI Effect in Amorphous Microwires
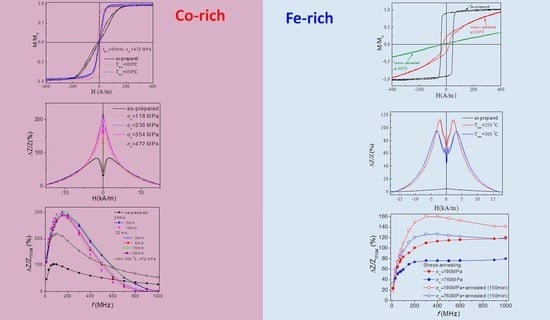
4.1. Tailoring of Magnetic Properties and GMI Effect in Co-Rich Amorphous Microwires
4.2. Engineering of Magnetic Softness and GMI Effect in Amorphous Microwires with Positive Magnetostriction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fiorillo, F.; Bertotti, G.; Appino, C.; Pasquale, M. Soft Magnetic Materials. In Wiley Encyclopedia of Electrical and Electronics Engineering; Webster, J., Ed.; John Wiley & Sons, Inc.: Torino, Italy, 1999; p. 42. [Google Scholar] [CrossRef]
- Lenz, J.; Edelstein, A.S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Herzer, G. Magnetic materials for electronic article surveillance. J. Magn. Magn. Mater. 2003, 254–255, 598–602. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Corte-Leon, P.; Blanco, J.M.; Zhukova, V. Advanced functional magnetic microwires for magnetic sensors suitable for biomedical applications. In Magnetic Materials and Technologies for Medical Applications; Tishin, A.M., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; Ch. 18. [Google Scholar] [CrossRef]
- Ripka, P.; Vertesy, G. Sensors based on soft magnetic materials Panel discussion. J. Magn. Magn. Mater. 2000, 215, 795–799. [Google Scholar] [CrossRef]
- Morón, C.; Cabrera, C.; Morón, A.; García, A.; González, M. Magnetic Sensors Based on Amorphous Ferromagnetic Materials: A Review. Sensors 2015, 15, 28340–28366. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Díaz-Michelena, M. Small Magnetic Sensors for Space Applications. Sensors 2009, 9, 2271–2288. [Google Scholar] [CrossRef] [PubMed]
- Baibich, M.N.; Broto, J.M.; Fert, A.; Nguyen Van Dau, F.; Petron, F.; Etienne, P.; Creuzer, G.; Friederich, A.; Chazelas, J. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 1988, 61, 2472. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inoue, J.; Maekawa, S. Theory of tunneling magnetoresistance in granular magnetic films. Phys. Rev. B 1996, 53, R11927. [Google Scholar] [CrossRef]
- Hasegawa, R. Applications of Amorphous Magnetic Alloys. In Properties and Applications of Nanocrystalline Alloys from Amorphous Precursors; Idzikowski, B., Švec, P., Miglierini, M., Eds.; NATO Science Series (Series II: Mathematics, Physics and Chemistry); Springer: Dordrecht, The Netherlands, 2005; Volume 184, pp. 189–198. [Google Scholar]
- Schuh, C.A.; Hufnagel, T.C.; Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 2007, 55, 4067–4109. [Google Scholar] [CrossRef]
- Hagiwara, M.; Inoue, A.; Masumoto, T. Mechanical properties of Fe–Si–B amorphous wires produced by in-rotating-water spinning method. Metall. Trans. A 1982, 13, 373–382. [Google Scholar] [CrossRef]
- Goto, T.; Nagano, M.; Wehara, N. Mechanical properties of amorphous Fe80P16C3B1 filament produced by glass-coated melt spinning. Trans. Jpn. Inst. Met. 1977, 18, 759–764. [Google Scholar] [CrossRef] [Green Version]
- Zhukova, V.; Cobeño, A.F.; Zhukov, A.; de Arellano Lopez, A.R.; López-Pombero, S.; Blanco, J.M.; Larin, V.; Gonzalez, J. Correlation between magnetic and mechanical properties of devitrified glass-coated Fe71.8Cu1Nb3.1Si15B9.1 microwires. J. Magn. Magn. Mater. 2002, 249, 79–84. [Google Scholar] [CrossRef]
- Masumoto, T.; Hashimoto, K. Corrosion properties of amorphous metals. J. Phys. Colloq. 1980, 41, C8-894–C8-900. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Panina, L.V.; Yamamoto, M.; Bushida, K. Recent Advances of Amorphous Wire CMOS IC Magneto-Impedance Sensors: Innovative High-Performance Micromagnetic Sensor Chip. J. Sens. 2015, 2015, 718069. [Google Scholar] [CrossRef] [Green Version]
- Zhukova, V.; Corte-Leon, P.; Blanco, J.M.; Ipatov, M.; Gonzalez, J.; Zhukov, A. Electronic Surveillance and Security Applications of Magnetic Microwires. Chemosensors 2021, 9, 100. [Google Scholar] [CrossRef]
- Honkura, Y.; Honkura, S. The Development of ASIC Type GSR Sensor Driven by GHz Pulse Current. Sensors 2020, 20, 1023. [Google Scholar] [CrossRef] [Green Version]
- Sabol, R.; Klein, P.; Ryba, T.; Hvizdos, L.; Varga, R.; Rovnak, M.; Sulla, I.; Mudronova, D.; Galik, J.; Polacek, I.; et al. Novel Applications of Bistable Magnetic Microwires. Acta Phys. Pol. A 2017, 131, 1150–1152. [Google Scholar] [CrossRef]
- Makhnovskiy, D.; Fry, N.; Zhukov, A. On different tag reader architectures for bistable microwires. Sens. Actuat. A Phys. 2011, 166, 133–140. [Google Scholar] [CrossRef]
- Von Gutfeld, R.J.; Dicello, J.F.; McAllister, S.J.; Ziegler, J.F. Amorphous magnetic wires for medical locator applications. Appl. Phys. Lett. 2002, 81, 1913–1915. [Google Scholar] [CrossRef]
- Kozejova, D.; Fecova, L.; Klein, P.; Sabol, R.; Hudak, R.; Sulla, I.; Mudronova, D.; Galik, J.; Varga, R. Biomedical applications of glass-coated microwires. J. Magn. Magn. Mater. 2019, 470, 2–5. [Google Scholar] [CrossRef]
- Zhukov, A.; Cobeño, A.F.; Gonzalez, J.; Blanco, J.M.; Aragoneses, P.; Dominguez, L. Magnetoelastic sensor of level of the liquid based on magnetoelastic properties of Co-rich microwires. Sens. Actuat. A Phys. 2000, 81, 129–133. [Google Scholar] [CrossRef]
- Praslička, D.; Blažek, J.; Šmelko, M.; Hudák, J.; Čverha, A.; Mikita, I.; Varga, R.; Zhukov, A. Possibilities of Measuring Stress and Health Monitoring in Materials Using Contact-Less Sensor Based on Magnetic Microwires. IEEE Trans. Magn. 2013, 49, 128–131. [Google Scholar] [CrossRef]
- Talaat, A.; Alonso, J.; Zhukova, V.; Garaio, E.; García, J.A.; Srikanth, H.; Phan, M.H.; Zhukov, A. Ferromagnetic glass-coated microwires with good heating properties for magnetic hyperthermia. Sci. Rep. 2016, 6, 39300. [Google Scholar] [CrossRef]
- Mitxelena-Iribarren, O.; Campisi, J.; Martínez de Apellániz, I.; Lizarbe-Sancha, S.; Arana, S.; Zhukova, V.; Mujika, M.; Zhukov, A. Glass-coated ferromagnetic microwire-induced magnetic hyperthermia for in vitro cancer cell treatment. Mater. Sci. Eng. C 2020, 106, 110261. [Google Scholar] [CrossRef]
- Qin, F.X.; Peng, H.X.; Phan, M.H.; Panina, L.V.; Ipatov, M.; Zhukov, A. Effects of wire properties on the field-tunable behaviour of continuous-microwire composites. Sens. Actuat. A Phys. 2012, 178, 118–125. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar]
- Beach, R.; Berkowitz, A. Giant magnetic field dependent impedance of amorphous FeCoSiB wire. Appl. Phys. Lett. 1994, 64, 3652–3654. [Google Scholar] [CrossRef]
- Knobel, M.; Vazquez, M.; Kraus, L. Giant magnetoimpedance. In Handbook of Magnetic Materials; Bruck, E., Ed.; Elsevier: Amsterdam, The Netherlands, 2003; Volume 15, pp. 497–563. [Google Scholar]
- Zhukov, A.; Ipatov, M.; Corte-León, P.; Gonzalez-Legarreta, L.; Churyukanova, M.; Blanco, J.M.; Gonzalez, J.; Taskaev, S.; Hernando, B.; Zhukova, V. Giant magnetoimpedance in rapidly quenched materials. J. Alloys Compd. 2020, 814, 152225. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Corte-León, P.; Gonzalez-Legarreta, L.; Blanco, J.M.; Zhukova, V. Soft Magnetic Microwires for Sensor Applications. J. Magn. Magn. Mater. 2020, 498, 166180. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Panina, L.V. Recent advances of micro magnetic sensors and sensing application. Sens. Actuat. A Phys. 1997, 59, 1–8. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Shen, L.P.; Cai, C.M.; Panina, L.V. Amorphous wire and CMOS IC-based sensitive micro-magnetic sensors (MI sensor and SI sensor) for intelligent measurements and controls. J. Magn. Magn. Mater. 2002, 249, 351–356. [Google Scholar] [CrossRef]
- Dufay, B.; Saez, S.; Dolabdjian, C.; Melo, L.G.C.; Yelon, A.; Ménard, D. Development of a high sensitivity Giant Magneto-Impedance magnetometer: Comparison with a commercial Flux-Gate. IEEE Trans. Magn. 2013, 49, 85. [Google Scholar] [CrossRef] [Green Version]
- Uchiyama, T.; Mohri, K.; Nakayama, S. Measurement of Spontaneous Oscillatory Magnetic Field of Guinea-Pig Smooth Muscle Preparation Using Pico-Tesla Resolution Amorphous Wire Magneto-Impedance Sensor. IEEE Trans. Magn. 2011, 47, 3070–3073. [Google Scholar] [CrossRef]
- Chen, L.; Bao, C.C.; Yang, H.; Li, D.; Lei, C.; Wang, T.; Hu, H.Y.; He, M.; Zhou, Y.; Cui, D.X. A prototype of giant magnetoimpedance-based biosensing system for targeted detection of gastric cancer cells. Biosens. Bioelectron. 2011, 26, 3246–3253. [Google Scholar] [CrossRef] [PubMed]
- Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Larin, V.; Gonzalez, J. Magnetoelastic sensor based on GMI of amorphous microwire. Sens. Actuat. A Phys. 2001, 91, 95–98. [Google Scholar] [CrossRef]
- Qin, F.X.; Pankratov, N.; Peng, H.X.; Phan, M.H.; Panina, L.V.; Ipatov, M.; Zhukova, V.; Zhukov, A.; Gonzalez, J. Novel magnetic microwires-embedded composites for structural health monitoring applications. J. Appl. Phys. 2010, 107, 09A314. [Google Scholar] [CrossRef]
- González-Alonso, D.; González-Legarreta, L.; Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Zhukov, A. Magnetoimpedance Response and Field Sensitivity in Stress-Annealed Co-Based Microwires for Sensor Applications. Sensors 2020, 20, 3227. [Google Scholar] [CrossRef]
- Vazquez, M.; Chen, D.-X. The magnetization reversal process in amorphous wires. IEEE Trans. Magn. 1995, 31, 1229–1238. [Google Scholar] [CrossRef]
- Mohri, K.; Humphrey, F.B.; Kawashima, K.; Kimura, K.; Muzutani, M. Large Barkhausen and Matteucci Effects in FeCoSiB, FeCrSiB, and FeNiSiB Amorphous Wires. IEEE Trans. Magn. 1990, 26, 1789–1791. [Google Scholar] [CrossRef]
- Zhukova, V.; Zhukov, A.; Blanco, J.M.; Gonzalez, J.; Ponomarev, B.K. Switching field fluctuations in a glass coated Fe-rich amorphous microwire. J. Magn. Magn. Mat. 2002, 249, 131–135. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Chizhik, A.; Ipatov, M.; Zhukov, A. AC-current-induced magnetization switching in amorphous microwires. Front. Phys. 2018, 13, 137501. [Google Scholar] [CrossRef]
- Zhukova, V.; Corte-Leon, P.; González-Legarreta, L.; Talaat, A.; Blanco, J.M.; Ipatov, M.; Olivera, J.; Zhukov, A. Review of Domain Wall Dynamics Engineering in Magnetic Microwires. Nanomaterials 2020, 10, 2407. [Google Scholar] [CrossRef] [PubMed]
- Ogasawara, I.; Ueno, S. Preparation and properties of amorphous wires. IEEE Trans. Magn. 1995, 31, 1219–1223. [Google Scholar] [CrossRef]
- Rudkowski, P.; Rudkowska, G.; Strom-Olsen, J.O. The fabrication of fine metallic fibers by continuous melt extraction and their magnetic and mechanical properties. Mater. Sci. Eng. A 1991, 133, 158–161. [Google Scholar] [CrossRef]
- Zhukova, V.; Zhukov, A.; Kraposhin, V.; Prokoshin, A.; Gonzalez, J. Magnetic properties and GMI of soft magnetic amorphous fibers. Sens. Actuat. A Phys. 2003, 106, 225–229. [Google Scholar] [CrossRef]
- Baranov, S.A.; Larin, V.S.; Torcunov, A.V. Technology, Preparation and Properties of the Cast Glass-Coated Magnetic Microwires. Crystals 2017, 7, 136. [Google Scholar] [CrossRef]
- Chiriac, H.; Lupu, N.; Stoian, G.; Ababei, G.; Corodeanu, S.; Óvári, T.-A. Ultrathin nanocrystalline magnetic wires. Crystals 2017, 7, 48. [Google Scholar] [CrossRef] [Green Version]
- Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; González, J.; Churyukanova, M.; Taskaev, S.; Zhukov, A. The effect of annealing on magnetic properties of “Thick” microwires. J. Alloys Compd. 2020, 831, 150992. [Google Scholar] [CrossRef]
- Taylor, G.F. A Method of Drawing Metallic Filaments and a Discussion of their Properties and Uses. Phys. Rev. 1924, 23, 655. [Google Scholar] [CrossRef]
- Ulitovsky, A.V.; Avernin, N.M. Method of Fabrication of Metallic Microwire. USSR Patent 161325, 19.03.64, Bulletin No. 7, 19 March 1964. [Google Scholar]
- Kraus, L.; Schneider, J.; Wiesner, H. Ferromagnetic resonance in amorphous alloys prepared by rapid quenching from the melt. Czech. J. Phys. B 1976, 26, 601–602. [Google Scholar] [CrossRef]
- Zhukov, A.; Zhukova, V.; González, J.; Larin, V.S.; Torcunov, A.V. Glass-Coated Ultrafine Amorphous Wires Having a Giant Magnetoimpedance (GMI) Effect at High Frequencies. European Patent EP2148338A1, 27 January 2010. [Google Scholar]
- Zhukov, A.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Hernando, B.; Gonzalez-Legarreta, L.; Suñol, J.J.; Zhukova, V. Correlation of Crystalline Structure with Magnetic and Transport Properties of Glass-Coated Microwires. Crystals 2017, 7, 41. [Google Scholar] [CrossRef]
- Badinter, E.Y.A.; Berman, N.R.; Drabenko, I.F.; Zaborovsky, V.I.; Zelikovsky, Z.I.; Cheban, V.G. Cast Microwires and Its Properties; Shtinica: Kishinev, USSR, 1973. [Google Scholar]
- Zhukov, A.; Shuvaeva, E.; Kaloshkin, S.; Churyukanova, M.; Kostitcyna, E.; Zhdanova, M.; Talaat, A.; Ipatov, M.; Zhukova, V. Studies of interfacial layer and its effect on magnetic properties of glass-coated microwires. J. Electr. Mater. 2016, 45, 2381–2387. [Google Scholar] [CrossRef]
- Zhukov, A.; Kostitcyna, E.; Shuvaeva, E.; Kaloshkin, S.; Churyukanova, M.; Sudarchikova, V.; Talaat, A.; Zhukova, V. Effect of composite origin on magnetic properties of glass-coated microwires. Intermetallics 2014, 44, 88–93. [Google Scholar] [CrossRef]
- Zhukov, A.; Shuvaeva, E.; Kaloshkin, S.; Churyukanova, M.; Kostitcyna, E.; Talaat, A.; Ipatov, M.; Gonzalez, J.; Zhukova, V. Studies of the Defects Influence on Magnetic Properties of Glass-Coated Microwires. IEEE Trans. Magn. 2014, 50, 2006604. [Google Scholar] [CrossRef]
- Zhukov, A.; Shuvaeva, E.; Kaloshkin, S.; Churyukanova, M.; Kostitcyna, E.; Sudarchikova, V.; Talaat, A.; Ipatov, M.; Zhukova, V. Influence of the defects on magnetic properties of glass-coated microwires. J. Appl. Phys. 2014, 115, 17A305. [Google Scholar] [CrossRef]
- Velázquez, J.; Vázquez, M.; Hernando, A.; Savage, H.T.; Wun-Fogle, M. Magnetoelastic anisotropy in amorphous wires due to quenching. J. Appl. Phys. 1991, 70, 6525–6527. [Google Scholar] [CrossRef]
- Antonov, A.S.; Borisov, V.T.; Borisov, O.V.; Prokoshin, A.F.; Usov, N.A. Residual quenching stresses in glass-coated amorphous ferromagnetic microwires. J. Phys. D Appl. Phys. 2000, 33, 1161–1168. [Google Scholar] [CrossRef]
- Chiriac, H.; Óvári, T.-A.; Corodeanu, S.; Ababei, G. Interdomain wall in amorphous glass-coated microwires. Phys. Rev. B 2007, 76, 214433. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Zhukov, A. Magnetoelastic contribution in domain wall dynamics of amorphous microwires. Phys. B 2012, 407, 1450–1454. [Google Scholar] [CrossRef]
- Astefanoaei, I.; Radu, D.; Chiriac, H. Internal stress distribution in DC joule-heated amorphous glass-covered microwires. J. Condens. Matter. Phys. 2006, 18, 2689–2716. [Google Scholar] [CrossRef]
- Torcunov, A.V.; Baranov, S.A.; Larin, V.S. The internal stresses dependence of the magnetic properties of cast amorphous microwires covered with glass insulation. J. Magn. Magn. Mater. 1999, 196–197, 835–836. [Google Scholar] [CrossRef]
- Gonzalez-Legarreta, L.; Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Optimization of magnetic properties and GMI effect of Thin Co-rich Microwires for GMI Microsensors. Sensors 2020, 20, 1558. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, A.; Talaat, A.; Ipatov, M.; Zhukova, V. Tailoring of High Frequency Giant Magnetoimpedance Effect of amorphous Co-rich microwires. IEEE Magn. Lett. 2015, 6, 2500104. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Corte-Leon, P.; Blanco, J.M.; González-Legarreta, L.; Zhukova, V. Routes for Optimization of Giant Magnetoimpedance Effect in Magnetic Microwires. IEEE Instrum. Meas. Mag. 2020, 23, 56–63. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Tailoring of magnetoimpedance effect and magnetic softness of Fe-rich glass-coated microwires by stress-annealing. Sci. Rep. 2018, 8, 3202. [Google Scholar] [CrossRef] [Green Version]
- Churyukanova, M.; Semenkova, V.; Kaloshkin, S.; Shuvaeva, E.; Gudoshnikov, S.; Zhukova, V.; Shchetinin, I.; Zhukov, A. Magnetostriction investigation of soft magnetic microwires. Phys. Status Solidi A 2016, 213, 363–367. [Google Scholar] [CrossRef]
- Usov, N.; Antonov, A.; Dykhne, A.; Lagar’kov, A. Stress dependence of the hysteresis loops of Co-rich amorphous wire. J. Phys. Condens. Matter. 1998, 10, 2453–2463. [Google Scholar] [CrossRef]
- Nderu, J.N.; Yamasaki, J.; Humphrey, F. Switching mechanism in Co based amorphous wire. J. Appl. Phys. 1997, 81, 4036–4038. [Google Scholar] [CrossRef]
- Zhukova, V.; Corte-Leon, P.; González-Legarreta, L.; Talaat, A.; Blanco, J.M.; Ipatov, M.; Olivera, J.; Zhukov, A. Optimization of Magnetic Properties of Magnetic Microwires by Post-Processing. Processes 2020, 8, 1006. [Google Scholar] [CrossRef]
- Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Churyukanova, M.; Baraibar, J.M.; Taskaev, S.; Zhukov, A. Stress dependence of the magnetic properties of glass-coated amorphous microwires. J. Alloys Compd. 2019, 789, 201–208. [Google Scholar] [CrossRef]
- Zhukova, V.; Corte-Leon, P.; Ipatov, M.; Blanco, J.M.; Gonzalez-Legarreta, L.; Zhukov, A. Development of Magnetic Microwires for Magnetic Sensor Applications. Sensors 2019, 19, 4767. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhukova, V.; Blanco, J.M.; Rodionova, V.; Ipatov, M.; Zhukov, A. Domain wall propagation in micrometric wires: Limits of single domain wall regime. J. Appl. Phys. 2012, 111, 07E311. [Google Scholar] [CrossRef]
- Chen, D.-X.; Dempsey, N.M.; Vázquez, M.; Hernando, A. Propagating domain wall shape and dynamics in iron-rich amorphous wires. IEEE Trans. Magn. 1995, 31, 781–790. [Google Scholar] [CrossRef]
- Richter, K.; Varga, R.; Kováč, J.; Zhukov, A. Controlling the Domain Wall Dynamics by Induced Anisotropies. IEEE Trans. Magn. 2012, 48, 1266–1268. [Google Scholar] [CrossRef]
- Zhukov, A.; Blanco, J.M.; Ipatov, M.; Zhukova, V. Fast magnetization switching in thin wires: Magnetoelastic and defects contributions. IEEE Sens. Lett. 2013, 11, 170–176. [Google Scholar] [CrossRef]
- Zhukova, V.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Churyukanova, M.; Zhukov, A. Effect of stress annealing on magnetic properties and GMI effect of Co- and Fe-rich microwires. J. Alloys Compd. 2017, 707, 189–194. [Google Scholar] [CrossRef]
- Gonzalez-Legarreta, L.; Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Route of magnetoimpedance and domain walls dynamics optimization in Co-based microwires. J. Alloys Compd. 2020, 830, 154576. [Google Scholar] [CrossRef]
- Zhukov, A.; Gonzalez-Legarreta, L.; Corte-Leon, P.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukova, V. Tailoring of Magnetic Softness and Magnetoimpedance of Co-rich Microwires by Stress-annealing. Phys. Stat. Solidi A 2021, 218, 2100130. [Google Scholar] [CrossRef]
- González, J.; Vázquez, M.; Barandiarán, J.M.; Madurga, V.; Hernando, A. Different kinds of magnetic anisotropies induced by current annealing in metallic glasses. J. Magn. Magn. Mater. 1987, 68, 151–156. [Google Scholar] [CrossRef]
- Luborsky, F.E.; Walter, J.L. Magnetic Anneal Anisotropy in Amorphous Alloys. IEEE Trans. Magn. 1977, 13, 953–956. [Google Scholar] [CrossRef]
- Haimovich, J.; Jagielinski, T.; Egami, T. Magnetic and structural effects of anelastic deformation of an amorphous alloy. J. Appl. Phys. 1985, 57, 3581. [Google Scholar] [CrossRef]
- Ohnuma, M.; Herzer, G.; Kozikowski, P.; Polak, C.; Budinsky, V.; Koppoju, S. Structural anisotropy of amorphous alloys with creep-induced magnetic anisotropy. Acta Mater. 2012, 60, 1278–1286. [Google Scholar] [CrossRef]
- Herzer, G. Amorphous and nanocrystalline soft magnets. In Proceedings of the NATO Advanced Study Institute on Magnetic Hysteresis in Novel Materials, Mykonos, Greece, 1–12 July 1996; Hadjipanayis, G.C., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; Volume 338, pp. 711–730, NATO ASI Series (Series E: Applied Sciences). [Google Scholar]
- Pirota, K.R.; Kraus, L.; Chiriac, H.; Knobel, M. Magnetic properties and GMI in a CoFeSiB glass-covered microwire. J. Magn. Magn. Mater. 2000, 21, L243–L247. [Google Scholar] [CrossRef]
- Zhukova, V.; Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Puerta, S.; Gonzalez, J.; Vázquez, M. Tailoring of magnetic properties of glass coated microwires by current annealing. J. Non-Cryst. Solids 2001, 287, 31–36. [Google Scholar] [CrossRef]
- Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Engineering of magnetic properties of Co-rich microwires by joule heating. Intermetallics 2019, 105, 92–98. [Google Scholar] [CrossRef]
- Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Zhukov, A. Effect of Joule heating on giant magnetoimpedance effect and magnetic properties of Co-rich microwires. J. Alloys Compd. 2021, 883, 160778. [Google Scholar] [CrossRef]
- Nematov, M.G.; Baraban, I.; Yudanov, N.A.; Rodionova, V.; Qin, F.X.; Peng, H.-X.; Panina, L.V. Evolution of the magnetic anisotropy and magnetostriction in Co-based amorphous alloys microwires due to current annealing and stress-sensory applications. J. Alloys Compd. 2020, 837, 155584. [Google Scholar] [CrossRef]
- Blanco, J.M.; Zhukov, A.; Gonzalez, J. Torsional Stress Impedance and Magneto-impedance in (Co0.95Fe0.05)72.5Si12.5B15 Amorphous Wire with Helical Induced Anisotropy. J. Phys. D Appl. Phys. 1999, 37, 3140–3145. [Google Scholar] [CrossRef]
- Popova, A.V.; Odintsov, V.I.; Menshov, S.A.; Kostitsyna, E.V.; Tarasov, V.P.; Zhukova, V.; Zhukov, A.; Gudoshnikov, S.A. Continuous control of a resistance in Co-rich amorphous ferromagnetic microwires during DC Joule heating. Intermetallics 2018, 99, 39–43. [Google Scholar] [CrossRef]
- Zhukova, V.; Ipatov, M.; González, J.; Blanco, J.M.; Zhukov, A.P. Development of Thin Microwires with Enhanced Magnetic Softness and GMI. IEEE Trans. Magn. 2008, 44, 3958–3961. [Google Scholar] [CrossRef]
- Kohmoto, O.; Ohya, K.; Yamaguchi, N.; Fujishima, H.; Ojima, T. Amorphous FeCoNiSiB alloys having zero magnetostriction. J. Appl. Phys. 1980, 51, 4342. [Google Scholar] [CrossRef]
- Schafer, R.; Ho, W.K.; Yamasaki, J.; Hubert, A.; Humphrey, F.B. Anisotropy pinning of domain walls in a soft amorphous magnetic material. IEEE Trans. Magn. 1991, 27, 3678–3689. [Google Scholar] [CrossRef]
- Nielsen, O.V.; Nielsen, H.J.V. Stress and field-induced magnetic anisotropy in metallic glasses with positive or negative λs. Solid Stat. Commun. 1980, 35, 281–284. [Google Scholar] [CrossRef]
- Barandiarán, J.M.; Hernando, A.; Madurga, V.; Nielsen, O.V.; Vázquez, M.; Vázquez-López, M. Temperature, stress, and structural-relaxation dependence of the magnetostriction in (Co0.94Fe0.06)75Si15B10 glasses. Phys. Rev. B 1987, 35, 5066–5071. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhukov, A.; Talaat, A.; Churyukanova, M.; Kaloshkin, S.; Semenkova, V.; Ipatov, M.; Blanco, J.M.; Zhukova, V. Engineering of magnetic properties and GMI effect in Co-rich amorphous microwires. J. Alloys Compd. 2016, 664, 235–241. [Google Scholar] [CrossRef]
- Corte-Leon, P.; Zhukova, V.; Blanco, J.M.; González-Legarreta, L.; Ipatov, M.; Zhukov, A.A. Stress-induced Magnetic Anisotropy Enabling Engineering of Magnetic Softness of Fe-rich Amorphous Microwires. J. Magn. Magn. Mater. 2020, 510, 166939. [Google Scholar] [CrossRef]
- Zhukov, A.; Churyukanova, M.; Kaloshkin, S.; Semenkova, V.; Gudoshnikov, S.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Zhukova, V. Effect of annealing on magnetic properties and magnetostriction coefficient of Fe–Ni-based amorphous microwires. J. Alloys Compd. 2015, 651, 718–723. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Corte-Leon, P.; Ipatov, M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Grading the magnetic anisotropy and engineering the domain wall dynamics in Fe-rich microwires by stress-annealing. Acta Mater. 2018, 155, 279–285. [Google Scholar] [CrossRef]
- Usov, N.A.; Antonov, A.S.; Lagar'kov, A.N. Theory of giant magneto-impedance effect in amorphous wires with different types of magnetic anisotropy. J. Magn. Magn. Mater. 1998, 185, 159–173. [Google Scholar] [CrossRef]
- Corte-Leon, P.; Zhukova, V.; Blanco, J.M.; Ipatov, M.; Taskaev, S.; Churyukanova, M.; Gonzalez, J.; Zhukov, A. Engineering of magnetic properties and magnetoimpedance effect in Fe-rich microwires by reversible and irreversible stress-annealing anisotropy. J. Alloys Compd. 2021, 855, 157460. [Google Scholar] [CrossRef]
- Zhukov, A.; Corte-Leon, P.; Gonzalez-Legarreta, L.; Ipatov, M.; Blanco, J.M.; Gonzalez, A.; Zhukova, V. Advanced functional magnetic microwires for technological applications. J. Phys. D Appl. Phys. submitted.
- Gonzalez, A.; Zhukova, V.; Ipatov, M.; Corte-Leon, P.; Blanco, J.M.; Zhukov, A. Effect of Joule heating on GMI and magnetic properties of Fe-rich glass-coated microwires. AIP Adv. in press.
- Zhukov, A.; Zhukova, V.; Larin, V.; Blanco, J.M.; Gonzalez, J. Tailoring of magnetic anisotropy of Fe-rich microwires by stress induced anisotropy. Phys. B 2006, 384, 1–4. [Google Scholar] [CrossRef]
- Goto, T. Fe–B and Fe–Si–B system alloy filaments produced by glass-coated melt spinning. Trans. Jpn. Inst. Met. 1980, 21, 219–224. [Google Scholar] [CrossRef] [Green Version]
- Corte-León, P.; Zhukova, V.; Blanco, J.M.; Chizhik, A.; Ipatov, M.; Gonzalez, J.; Fert, A.; Zhukov, A. Engineering of domain wall propagation in magnetic microwires with graded magnetic anisotropy. Appl. Mater. Today 2021, 101263. [Google Scholar] [CrossRef]
- Skomski, R.; George, T.A.; Sellmyer, D.J. Nucleation, and wall motion in graded media. J. Appl. Phys. 2008, 103, 07F531. [Google Scholar] [CrossRef] [Green Version]
- Tsai, J.-L.; Tzeng, H.-T.; Liu, B.-F. Magnetic properties and microstructure of graded Fe/FePt films. J. Appl. Phys. 2010, 107, 113923. [Google Scholar] [CrossRef]
- Zha, C.L.; Dumas, R.K.; Fang, Y.Y.; Bonanni, V.; Nogués, J.; Åkerman, J. Continuously graded anisotropy in single (Fe53Pt47)100−xCux films. Appl. Phys. Lett. 2010, 97, 182504. [Google Scholar] [CrossRef] [Green Version]
- Kronmüller, H. Micromagnetism and microstructure of amorphous alloys. J. Appl. Phys. 1981, 52, 1859–1864. [Google Scholar] [CrossRef]
- Kronmüller, H.; Fähnle, M.; Domann, M.; Grimm, H.; Grimm, R.; Groger, B. Magnetic properties of amorphous ferromagnetic alloys. J. Magn. Magn. Mater. 1979, 13, 53–70. [Google Scholar] [CrossRef]
- Kronmüller, H.; Groger, B. Domains, domain walls and the coercive field of amorphous ferromagnets. J. Phys. 1981, 42, 1285–1292. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Qin, F.X.; Xing, D.W.; Cao, F.Y.; Wang, X.D.; Peng, H.X.; Sun, J.F. Relating residual stress and microstructure to mechanical and giant magneto-impedance properties in cold-drawn Co-based amorphous microwires. Acta Mater. 2012, 60, 5425–5436. [Google Scholar] [CrossRef]
- Phan, M.H.; Peng, H.X. Giant Magnetoimedance Materials: Fundamentals and Applications. Prog. Mater. Sci. 2008, 53, 323–420. [Google Scholar] [CrossRef]
- Ménard, D.; Britel, M.; Ciureanu, P.; Yelon, A. Giant magnetoimpedance in a cylindrical magnetic conductor. J. Appl. Phys. 1998, 84, 2805–2814. [Google Scholar] [CrossRef]
- Nakayama, K.S.; Chiba, T.; Tsukimoto, S.; Yokoyama, Y.; Shima, T.; Yabukami, S.H. Ferromagnetic resonance in soft-magnetic metallic glass nanowire and microwire. Appl. Phys. Lett. 2014, 105, 202403. [Google Scholar] [CrossRef]























| Composition | Metallic Nucleus Diameter, d (μm) | Total Diameter, D (μm) | Ratio ρ = d/D | Magnetostriction Coefficient, λs × 106 |
|---|---|---|---|---|
| Fe74B13Si11C2 | 16.6 | 20.8 | 0.8 | 38 |
| Fe74Si11B13C2 | 14.6 | 21.8 | 0.55 | 38 |
| Fe75B9Si12C4 | 15.2 | 17.2 | 0.88 | 38 |
| Fe65Si15B15C5 | 15 | 23.8 | 0.63 | 38 |
| Fe65Si15B15C5 | 10.8 | 22.5 | 0.48 | 38 |
| Fe65Si15B15C5 | 6 | 23.1 | 0.26 | 38 |
| Fe36Co40B12.9Si11.1 | 19.8 | 23.9 | 0.83 | 25 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 6.6 | 15.7 | 0.42 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 6.8 | 13.6 | 0.5 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 9.8 | 18.5 | 0.53 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 11.8 | 18.4 | 0.64 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 13.4 | 20.9 | 0.64 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 16.8 | 24 | 0.7 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 16.8 | 21 | 0.8 | −3 |
| Fe3.8Co65.4Ni1B13.8Si13Mo1.35C1.65 | 18.8 | 22.2 | 0.85 | −1 |
| Co69.2Fe3.6Ni1B12.5Si11Mo1.5C1.2 | 22.8 | 23.2 | 0.98 | −0.3 |
| Fe16Co60Si13B11 | 12 | 29 | 0.4 | 15 |
| Co41.7Fe36.4Si10.1B11.8 | 13.6 | 34 | 0.4 | 25 |
| Co41.7Fe36.4Si10.1B11.8 | 18 | 38 | 0.47 | 25 |
| Co41.7Fe36.4Si10.1B11.8 | 13.6 | 24.6 | 0.55 | 25 |
| Fe62Ni15.5Si7.5B15 | 14.35 | 33.25 | 0.43 | 27 |
| Co77.5Si15B7.5 | 13.1 | 18 | 0.73 | −5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhukova, V.; Corte-Leon, P.; Blanco, J.M.; Ipatov, M.; Gonzalez-Legarreta, L.; Gonzalez, A.; Zhukov, A. Development of Magnetically Soft Amorphous Microwires for Technological Applications. Chemosensors 2022, 10, 26. https://doi.org/10.3390/chemosensors10010026
Zhukova V, Corte-Leon P, Blanco JM, Ipatov M, Gonzalez-Legarreta L, Gonzalez A, Zhukov A. Development of Magnetically Soft Amorphous Microwires for Technological Applications. Chemosensors. 2022; 10(1):26. https://doi.org/10.3390/chemosensors10010026
Chicago/Turabian StyleZhukova, Valentina, Paula Corte-Leon, Juan Maria Blanco, Mihail Ipatov, Lorena Gonzalez-Legarreta, Alvaro Gonzalez, and Arcady Zhukov. 2022. "Development of Magnetically Soft Amorphous Microwires for Technological Applications" Chemosensors 10, no. 1: 26. https://doi.org/10.3390/chemosensors10010026
APA StyleZhukova, V., Corte-Leon, P., Blanco, J. M., Ipatov, M., Gonzalez-Legarreta, L., Gonzalez, A., & Zhukov, A. (2022). Development of Magnetically Soft Amorphous Microwires for Technological Applications. Chemosensors, 10(1), 26. https://doi.org/10.3390/chemosensors10010026