Infra-Red Plasmonic Sensors
Abstract
:1. Introduction
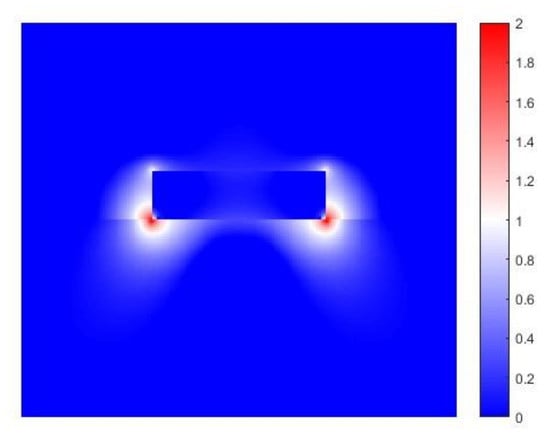
2. Metal Enhanced Fluorescence in the Near Infra-Red
3. Ge as a Plasmonic Material in the Mid Infra-Red
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Centeno, A.; Xie, F. An electromagnetic study of metal enhanced fluorescence due to immobilized particle arrays on glass substrate. Mater. Today Proc. 2015, 2, 94–100. [Google Scholar] [CrossRef]
- Wijaya, E.; Lenaerts, C.; Maricot, S.; Hastanin, J.; Habraken, S.; Vilcot, J.-P.; Boukherroub, R.; Szunerits, S. Surface plasmon resonance-based biosensors: From the development of different SPR structures to novel surface functionalization strategies. Curr. Opin. Solid State Mater. Sci. 2011, 15, 208–224. [Google Scholar] [CrossRef]
- Pranveer, S. SPR Biosensors: Historical Perspectives and Current Challenges. Sens. Actuators B Chem. 2016, 229, 110–130. [Google Scholar]
- Ashaduzzaman, Md.; Deshpande, S.R.; Murugan, N.A.; Misra, Y.K.; Turner, A.P.F.; Tiwari, A. On/off-switchable LSPR nano-immunoassay for troponin-T. Sci. Rep. 2017, 7, 44027. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Reddy, G.B. Stability-Inspired Entrapment of Ag Nanoparticles in ZrO2 Thin films. Plasmonics 2016, 11, 261. [Google Scholar] [CrossRef]
- Kumar, M.; Jangid, T.; Panchal, V.; Kumar, P.; Pathak, A. Effect of Grazing Angle Cross-Ion Irradiation on Ag Thin Films. Nanoscale Res. Lett. 2016, 11, 454. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Reddy, G.B. Tailoring surface plasmon resonance in Ag:ZrO2 nanocomposite thin films. Phys. E 2010, 43, 470–474. [Google Scholar] [CrossRef]
- Catchpole, K.R.; Polman, A. Plasmonic solar cells. Opt. Express 2008, 16, 21793–21800. [Google Scholar] [CrossRef] [PubMed]
- Atwater, H.A.; Polman, A. Plasmonics for improved photovoltaic devices. Nat. Mater. 2010, 9, 205–213. [Google Scholar] [CrossRef] [PubMed]
- Willets, K.A.; Van Duyne, R.P. Localised surface plasmon resonance spectroscopy and sensing. Annu. Rev. Phys. Chem. 2007, 58, 267–297. [Google Scholar] [CrossRef] [PubMed]
- Xie, F.; Baker, M.S.; Goldys, E.M. Homogeneous silver-coated nanoparticles for enhanced fluorescence detection. J. Phys. Chem. B 2006, 110, 23085–23091. [Google Scholar] [CrossRef] [PubMed]
- Lakowicz, J.R. Radiative Decay Engineering: Biophysical and Biomedical Applications. Anal. Biochem. 2001, 291, 1–24. [Google Scholar] [CrossRef] [PubMed]
- Lakowicz, J.R. Radiative decay engineering 5: Metal-enhanced fluorescence and plasmon emission. Anal. Biochem. 2005, 337, 171–194. [Google Scholar] [CrossRef] [PubMed]
- Geddes, C.D.; Parfenov, A.; Roll, D.; Fang, J.; Lakowicz, J.R. Electrochemical and Laser Deposition of Silver for Use in Metal-Enhanced Fluorescence. Langmuir 2003, 19, 6236–6241. [Google Scholar] [CrossRef] [PubMed]
- Lakowicz, J.R.; Geddes, C.D.; Gryczynski, I.; Malicka, J.; Gryczynski, Z.; Aslan, K.; Lukomska, J.; Matveeva, E.; Zhang, J.; Badugu, R.; et al. Advances in Surface-Enhanced Fluorescence. J. Fluoresc. 2004, 14, 425–441. [Google Scholar] [CrossRef] [PubMed]
- Pribik, R.; Dragan, A.I.; Zhang, Y.; Gaydos, C.; Geddes, C.D. Metal-Enhanced Fluorescence (MEF): Physical characterization of Silver-island films and exploring sample geometries. Chem. Phys. Lett. 2009, 478, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Ni, W.; Kou, K.; Zhang, S.; Sun, Z.; Sun, L.-D.; Wang, J.; Yan, C.-H. Incorporation of Gold Nanorods and Their Enhancement of Fluorescence in Mesostructured Silica Thin Films. J. Phys. Chem. C 2008, 112, 18895. [Google Scholar] [CrossRef]
- Sun, B.; Wang, C.; Han, S.; Huc, Y.; Zhangd, L. Metal-enhanced fluorescence-based multilayer core–shell Ag-nanocube@SiO2@PMOs nanocomposite sensor for Cu2+ detection. RSC ADV 2016, 6, 61109. [Google Scholar] [CrossRef]
- Xu, S.; Cao, Y.; Zhou, J.; Wang, X.; Wang, X.; Xu, W. Plasmonic enhancement of fluorescence on silver nanoparticle films. Nanotechnology 2011, 22, 275715. [Google Scholar] [CrossRef] [PubMed]
- Xia, B.; He, F.; Li, L. Metal-enhanced fluorescence using aggregated silver nanoparticles. Colloids Surf. A 2014, 444, 9–14. [Google Scholar] [CrossRef]
- Yang, B.; Lu, N.; Qi, D.; Ma, R.; Wu, Q.; Hao, J.; Liu, X.; Mu, Y.; Reboud, V.; Kehagias, N.; et al. Tuning the Intensity of Metal-Enhanced Fluorescence by Engineering Silver Nanoparticle Arrays. Small 2010, 6, 1038. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Theodorou, I.G.; Centeno, A.; Petrov, P.K.; Alford, N.M.; Ryan, M.P.; Xie, F. Gold nanodisc arrays as near infrared metal-enhanced fluorescence platforms with tuneable enhancement factors. J. Mater. Chem. C 2017, 5, 917–925. [Google Scholar] [CrossRef]
- Theodorou, I.G.; Jawad, Z.A.R.; Q, J.; Aboagye, E.O.; Porter, A.E.; Ryan, M.P.; Xie, F. Gold Nanostar Substrates for Metal-Enhanced Fluorescence through the First and Second Near-Infrared Windows. Chem. Mater. 2017, 29, 6916–6926. [Google Scholar] [CrossRef]
- Darvill, D.; Centeno, A.; Xie, F. Plasmonic fluorescence enhancement by metal nanostructures: Shaping the future of bionanotechnology. Phys. Chem. Chem. Phys. 2013, 15, 15709–15726. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Xie, F.; Baltar, H.T.M.C.M.; Goldys, E.M. Metal-enhanced fluorescence in the life sciences: Here, now and beyond. Phys. Chem. Chem. Phys. 2013, 15, 15695–15708. [Google Scholar] [CrossRef] [PubMed]
- Xie, F.; Centeno, A.; Ryan, M.R.; Riley, D.J.; Alford, N.M. Au nanostructures by colloidal lithography: From quenching to extensive fluorescence enhancement. J. Mater. Chem. B 2013, 1, 536–543. [Google Scholar] [CrossRef]
- Xie, F.; Pang, J.S.; Centeno, A.; Ryan, M.P.; Riley, D.J.; Alford, N.M. Nanoscale control of Ag nanostructures for plasmonic fluorescence enhancement of near-infrared dyes. Nano Res. 2013, 6, 496–510. [Google Scholar] [CrossRef] [Green Version]
- Drozdowicz-Tomsia, K.; Xie, F.; Goldys, E.M. Deposition of Silver Dentritic Nanostructures on Silicon for Enhanced Fluorescence. J. Phys. Chem. C 2010, 114, 1562–1569. [Google Scholar] [CrossRef]
- Prucnal, S.; Liu, F.; Voelskow, M.; Vines, L.; Rebohle, L.; Lang, D.; Berencén, Y.; Andic, S.; Boettger, R.; Helm, M.; et al. Ultra-doped n-type germanium thin films for sensing in the mid-infrared. Sci. Rep. 2016, 6, 27643. [Google Scholar] [CrossRef] [PubMed]
- Stanley, R. Plasmonics in the mid-infrared. Nat. Photon 2012, 6, 409–411. [Google Scholar] [CrossRef]
- Soref, R. Mid-infrared photonics in silicon and germanium. Nat. Photon 2010, 4, 495–497. [Google Scholar] [CrossRef]
- Baldassarre, L.; Sakat, E.; Frigerio, J.; Samarelli, A.; Gallacher, K.; Calandrini, E.; Isella, G.; Paul, D.J.; Ortolani, M.; Biagioni, P. Midinfrared plasmon-enhanced spectroscopy with germanium antennas on silicon substrates. Nano. Lett. 2015, 15, 7225–7231. [Google Scholar] [CrossRef] [PubMed]
- Frigerio, J.; Ballabio, A.; Isella, G.; Sakat, E.; Biagioni, P.; Bollani, M.; Napolitani, E.; Manganelli, E.; Virgilio, M.; Grupp, A.; et al. Tunability and losses of mid-infrared plasmonics in heavily doped germanium thin films. arXiv, 2016; arXiv:1601.05321v1. [Google Scholar]
- Bharadwaj, P.; Novotny, L. Spectral dependence of single molecule fluorescence enhancement. Opt. Express 2007, 15, 14266–14274. [Google Scholar] [CrossRef] [PubMed]
- Centeno, A.; Xie, F.; Alford, N. Predicting the fluorescent enhancement rate by gold amd silver nanospheres using finite-difference time-domain analysis. IET Nanobiotechnol. 2013, 7, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Liaw, J.W.; Chen, C.S.; Chen, J.H. Plasmonic effect of gold nanospheres on spontaneous emission. Prog. Electromagn. Res. B 2011, 31, 283–296. [Google Scholar] [CrossRef]
- Aziz, U.A.; Rashid, N.N.; Aid, S.R.; Centeno, A.; Akira, S.; Ikenoue, H.; Xie, F. Electrical and Structural Analysis on the Formation of n-type Junction in Germanium. IOP Conf. Ser. Mater. Sci. Eng. 2017, 204, 012003. [Google Scholar] [CrossRef]
- Aid, S.R.; Matsumoto, S.; Fuse, G. Boron diffusion behavior in silicon during shallow p+/n junction formation by non-melt excimer laser annealing. Phys. Status Solidi A 2011, 208, 1646–1651. [Google Scholar] [CrossRef]
- Aid, S.R.; Matsumoto, S.; Fuse, G.; Sakuragi, S. Comparison of boron diffusion in silicon during shallow p+/n junction formation by non-melt excimer and green laser annealing. Phys. Status Solidi A 2011, 208, 2772–2777. [Google Scholar] [CrossRef]
- Byrnes, S.J. Multilayer optical calculations. arXiv, 2016; arXiv:1603.02720. [Google Scholar]
- Centeno, A.; Ahmed, B.; Reehal, H.; Xie, F. Diffuse scattering from hemispherical nanoparticles at the air-silicon interface. Nanotechnology 2013, 24, 415402. [Google Scholar] [CrossRef] [PubMed]
- Kuzmenko, A. Guide to RefFIT Software to Fit Optical Spectra. 2015. Available online: https://sites.google.com/site/reffitprogram/home (accessed on 9 October 2017).
- Oskooi, A.F.; Roundy, D.; Ibanescu, M.; Bernel, P.; Joannopoulos, J.D.; Johnson, S.G. MEEP: A flexible free-software package for electromagnetic simulations by the FDTD method. Comput. Phys. Commun. 2010, 181, 687–702. [Google Scholar] [CrossRef]








| Fluorophore | Excitation Wavelength (nm) | Emission Wavelength (nm) | Fluorescent Enhancement Factor | Excitation Rate Enhancement (χ) | Emission Rate Enhancement (φm/φ°) | Type of Nanoparticle | Reference |
|---|---|---|---|---|---|---|---|
| AF 790 | 780 | 790 | 68.8 | - | - | Au, Nanotriangle | [26] |
| AF 790 | 780 | 790 | 83 | 11.5 | 7.2 | Ag, Nanotriangle | [27] |
| AF 750 | 730 | 750 | 235 | 25.2 | 9.3 | Au, Cylinder | [22] |
| AF 750 | 730 | 750 | 321 | 107 | 3 | Au, Nanostar | [23] |
| AF 790 | 780 | 790 | 195 | 18.6 | 10.5 | Au, Nanostar | [23] |
| Ag2QD | 780 | 1205 | 40 | - | - | Au, Nanostar | [23] |
| Material Number | η (cm−3) | ε∞ | ωp (cm−1) | ωc (cm−1) | γ (cm−1) | Sample Number in Reference [33] |
|---|---|---|---|---|---|---|
| 1 | 2.3 × 1019 | 16.5 | 4032 | 974.3 | 189.83 | 9338 |
| 2 | 3.0 × 1019 | 16.2 | 4705 | 1147.4 | 224.64 | 9336 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Centeno, A.; Aid, S.R.; Xie, F. Infra-Red Plasmonic Sensors. Chemosensors 2018, 6, 4. https://doi.org/10.3390/chemosensors6010004
Centeno A, Aid SR, Xie F. Infra-Red Plasmonic Sensors. Chemosensors. 2018; 6(1):4. https://doi.org/10.3390/chemosensors6010004
Chicago/Turabian StyleCenteno, Anthony, Siti Rahmah Aid, and Fang Xie. 2018. "Infra-Red Plasmonic Sensors" Chemosensors 6, no. 1: 4. https://doi.org/10.3390/chemosensors6010004
APA StyleCenteno, A., Aid, S. R., & Xie, F. (2018). Infra-Red Plasmonic Sensors. Chemosensors, 6(1), 4. https://doi.org/10.3390/chemosensors6010004