Empirical Modeling by Active Central Composite Rotatable Design: Orange 16 Dye Biosorption onto Biosorbents Based on Residual Bacterial Lactobacillus sp. Biomass

Abstract

(1) Background: This research work proposes the ‘passive’ biosorption study of Orange 16 dye onto residual Lactobacillus sp. biomass immobilized in sodium alginate using an experimental modeling design. (2) Methods: It was applied the batch biosorption methodology was applied with a real-time determination of residual dye content and biosorption efficiency (Y, %). Empirical planning was used based on an active central composite rotatable design of 2³ order in which three independent variables were considered, including residual biomass concentration (2.92–13.00 g/L, mean granule size of 0.7–1.0 mm) (X₁), temperature (8–42 °C) (X₂) and biosorption time (4–24 h) (X₃), in association with the considered dependent variable (Y). The proposed mathematical model was validated using a few statistical tools. (3) Results: The batch biosorption experiments were permitted to propose a mathematical model considering a basic value and variation step for each selected independent variable and then to validate it. The maximum experimental dye removal was 79.98% when 11 g/L immobilized biosorbent was applied in an 89.76 mg/L dye-containing solution at 15 °C and 20 h. The significance of each independent variable on dye removal was investigated and, most importantly, explained. (4) Conclusions: The residual Lactobacillus sp. biomass can be applied as an alternative biosorbent for anionic dye removal from an aqueous solution.

1. Introduction

Water is essential to all forms of plant and animal life [1]; its quality must be satisfactory for continued use. There are many mechanical–physical, chemical, and microbiological aspects to be considered when determining its acceptability for proper use, including its color and persistent organics content, among others. The additional color produced in water due to many residual synthetic dyes discharged or newly formed (i.e., aromatic species, hardly biodegradable as nitrosamines, etc.) may have negative effects on aquatic organisms due to the reduction in photosynthesis activity by the limitation of light penetration [2]. Water is often directly in contact with or incorporated into an industrial product. Most industries use water, often in large quantities, for numerous processing purposes; sometimes, little or none enters the final products and, thus, most, or all of it must be discharged or reused. The quality requirements of final effluent (treated wastewater) for further reuse/recycling, or directly discharged in natural water resources/aqueous receptors are specific and becoming more severe. Therefore, a corresponding water treatment is always required in an integrated treatment system that does not interfere with the industrial manufacturing process.

Among the physical–chemical treatment processes in use, adsorption/sorption/‘passive’ biosorption still remains an advanced method applied in any treatment step for the removal of toxic and persistent organics from polluting wastewater or final industrial effluent (onsite reused/recycled). Commonly, most organics can be readily adsorbed onto activated carbon (as a nonpolar sorbent), while polar substances require a polar sorbent as silica gel. A successful sorbent should not attract water (as silica gel does) and limit to adsorption/sorption/‘passive biosorption’ of nonpolar materials from treating water and wastewater. Contaminants in water and wastewater are nearly always mixtures of organic materials, and the nature of the mixture has an important effect on the sorptive characteristics. Thus, some mixtures result in enhanced adsorption, others in decreased adsorption.

The rate and efficiency of adsorption/sorption/‘passive biosorption’ are affected by environmental conditions and selected operating process parameters, especially in the sorption-based system using fixed bed with gravity (downflow) and/or fixed bed with pressure and fluidized beds (upflow). Thus, the adsorption equilibrium (described by corresponding equilibrium isotherms) moves toward the sorptive phase with decreasing temperatures, and therefore capacity can sometimes be expected to increase at a lower temperature [1]. The adsorption/sorption mechanism is specific to each treatment system primarily depending on the treating water/wastewater characteristics, equipment characteristics and facilities and control of operating adsorption/sorption/‘passive biosorption’ process parameters.

Experimental research recommends the alternative of using a new category of adsorbents called biosorbents, which are based on residual biomass for removal of persistent chemical pollutants [3,4,5], e.g., residual bacterial biomass in an immobilized form, especially with sodium alginate, among others. Moreover, the valorization of useful solid wastes, e.g., industrial and agricultural biomass in free forms, residual biomass (like microbial biomass) in the removal of persistent pollutants, responds to the requirements imposed by the ‘circular economy’ and the principles of sustainable waste hierarchy [4,5,6,7,8] where each waste can become useful raw material in manufacturing processes until ultimate waste (final waste, which is eliminated by incineration, or controlled landfilling storage/deposition after inactivation/neutralization). For efficient separation and ease of handling of ‘spent’ adsorbent/sorbent/biosorbent, the residual bacterial biomass can be immobilized in a polymeric matrix (sodium alginate) [9,10,11,12,13]. After various studies of adsorption/sorption/‘passive’ biosorption equilibrium, process thermodynamics and kinetic characterization, the application of modeling and optimization designs are required for transposing the process from the laboratory scale to real-world industrial systems. Thus, adequate mathematical models for further technological application must be controlled and, if possible, mathematically optimized [14,15,16].

Orange 16 is an anionic reactive dye, and its ‘passive’ biosorption from an aqueous system using residual biomass based on the mixture of Lactobacillus plantarum and Lactobacillus casei strains from the lactic acid production immobilized in sodium alginate was reported and analyzed, being found as corresponding to maximum biosorption capacities in the range of 46.512–227.273 mg/g viz. the Langmuir II model, or 121.2–418.719 mg/g viz. Dubinin–Radushkevich model, with a probable spontaneous mechanism of a predominantly physical type [12]. Afterward, this ‘passive’ biosorption is influenced by some operating process parameters, including temperature, pH, biosorption time/duration, biosorbency and dye concentrations in aqueous systems, as well as other characteristics, including the size of biosorbent granules and newly formed microspheres. The corresponding operational conditions must be found to ensure the highest degree of anionic dye removal from the aqueous system, and, consequently, the proposal of a mathematical model associated with its statistical validation and further optimization—it can then become a pertinent scientific data basis to scale up ‘passive’ biosorption in industrial scale setups.

The scientific literature has reported numerous experimental modeling designs, but we selected the empirical modeling design based on an active central composite rotatable design of 2³ order and further maximum values by the classical optimization methodology. The optimal value found to work with the newly prepared bacterial biomass-based biosorbent immobilized in sodium alginate sustained this possible alternative for the removal of anionic Orange 16 reactive dye from an aqueous system. The main aim of this paper is to propose a mathematical model tested for a description of the ‘passive’ biosorption of anionic Orange 16 reactive dye onto the newly prepared biosorbent based on the residual biomass of Lactobacillus sp. mixture immobilized in sodium alginate in terms of dye removal efficiency in aqueous solutions. For this purpose, the ‘passive’ biosorption of anionic dye will be studied considering the specific experimental planning design and the obtained experimental data referring to the remaining anionic Orange 16 dye concentration in an aqueous system, the dye removal efficiency (%), the effect of studied three independent variables on the dependent variable variation was analyzed and interpreted, with the results used for the mathematical model and possible operating control. It must be underlined that the newly prepared biosorbent material immobilized in sodium alginate was physicochemical/morphologically characterized before and after the anionic Orange 16 dye biosorption, and its results were reported in previous authors’ research [12] to demonstrate that the anionic dye biosorption took place, and its development and performance were underlined.

For the modeling of experimental data, a well-known design was used based on an active empirical design applied in various scientific research reports [17,18,19,20,21,22,23,24,25]. This proposed mathematical model is required for each technological process to estimate and control the experimental results if some variations of the operating process parameters take place, to anticipate the best value when multiple operating variables are considered, or to remediate some technical operating problems to maintain acceptable dye removal results.

2. Materials and Methods

2.1. Preparation of Residual Biomass-Based Biosorbent and Tested Contaminant

The tested biosorbent was processed in the laboratory from the residual biomass separated after centrifugation (8000 rpm) of the fermentation broth used for lactic acid production through a drying step for biomass (biological/enzymatic) inactivation and complete dewatering (no imposed special handling conditions for the dried solid material), and further immobilization by the stirring of 5% residual inactivated biomass in 1% sodium alginate solution prepared with distilled water at 70 °C. After complete homogenization, the mixture was dropped through capillaries into 1% calcium chloride prepared with distilled water at 5 °C to obtain spherical granules with 1–1.5 mm in diameter (Figure 1a) [12].

The prepared residual biomass-based biosorbent had a content of 5% dry weight (d.w.) of bacterial cells. The biosynthesis process of lactic acid was developed in a fermentation installation (capacity of 1 L) based on an anaerobic process, enzymatically developed by a mixture of two strains, meaning Lactobacillus plantarum and Lactobacillus casei. The biosorbent preparation and its characterization (SEM, FTIR) were presented in detail in our previous paper [12]. All chemicals required in the experiment were of analytical purity, used without further purification and purchased from Chemical Company SA (Iasi, Romania).

In the case of the tested contaminant (adsorbate) for this study, an anionic reactive dye, Orange 16 (O16) (MW = 617.54 g/mol, λ_max = 495 nm, from Sigma-Aldrich Co., St. Louis, MO, USA) with the chemical structure illustrated in Figure 1b, was selected as the principal/major contaminant (reference model of polluting species—an anionic reactive dye) of an aqueous system [12].

It was used in the commercial form of anionic reactive dye (powder) to prepare the stock dye solution (724 mg dye/L) and further working solutions (20–250 mg/L) by adequate dilution of the corresponding volume of stock dye solution with distilled water.

In all modeling experiments, according to the empirical planning design, the concentration of anionic reactive dye was kept constant at 89.76 mg/L for good dye removal results, performing as reported in previous experiments [12].

2.2. ‘Passive’ Biosorption Working Method

All experiments were performed in 100 mL Erlenmeyer flasks by using adequate weighted amounts of prepared immobilized biosorbent (established biosorbent concentration in an aqueous solution in the range of 2.92–13 g/L, granule with around 5% dry matter) with 25 mL of O16 dye solution with different initial concentrations (20–250 mg/L). The dye retained from the aqueous solution onto the prepared immobilized biosorbent is not an active biosorption based on a biological process but considered a physical (adsorption) and sometimes chemical (chemisorption) process, commonly a physical–chemical process (sorption) due to the inactivation of biological activity in an aqueous system. We considered this treatment process as ‘passive’ biosorption (the adsorptive material is of biological origin, but the treatment is of physical-chemical type).

The pH values were adjusted with the 0.1 N HCl solution at the value of pH = 2 (measured with a waterproof Hanna pH meter, Hanna Instruments Inc., Woonsocket, RI, USA) for the O16 dye ‘passive’ biosorption (highest adsorption capacities were obtained at pH 2) [12]. The working temperature (kept constant during the entire experiment) was selected in the range of 8–42 °C, and the biosorption time (S/L phases contact duration) was varied in range of 4–24 h. The remaining anionic O16 dye concentration in the aqueous solution was determined using the spectrophotometer-based method at the maximum dye wavelength of 495 nm, using the MeterTech SP-830 Plus spectrophotometer (MeterTech Inc., Taipei, Taiwan, version 1.06). The values of the dye removal or ‘passive’ biosorption efficiency (R, or Y, (%)) and ‘passive’ biosorption capacity (q, (mg/g)) were calculated with relations (1a) and (1b):

$$\mathrm{R} (\mathrm{or} \mathrm{Y}, \%)=\frac{{\mathrm{C}}_0-{\mathrm{C}}_{\mathrm{t}}}{{\mathrm{C}}_0}·100$$

(1a)

or

$$\mathrm{q}=\frac{{\mathrm{C}}_0-{\mathrm{C}}_{\mathrm{t}}}{\mathrm{G}·\mathrm{V}}$$

(1b)

where C₀ and C_t are the initial and remaining dye (at t biosorption time) concentration in the aqueous solution (mg/L), G is the biosorbent amount (g), and V is the aqueous solution volume (L).

2.3. Empirical Modeling of ‘Passive’ Dye Biosorption Process

In all of our ‘passive’ biosorption experiments performed in a laboratory-scale setup, for anionic O16 reactive dye removal from the aqueous solutions onto the residual Lactobacillus sp. biomass-based biosorbent immobilized in sodium alginate, the independent variables with significant influencing effects onto the dye’s ‘passive’ biosorption were selected as follows: the biosorbent concentration (coded variable—X₁ and in real terms—Z₁, [g/L]), temperature (coded—X₂ and as a real variable—Z₂, [°C]) and ‘passive’ biosorption time/duration (coded—X₃ and real variable—Z₃, [h]). The chosen dependent variable, also considered as the decision or response function and optimization criterion, was selected to be the anionic dye removal (Y, or R, [%]). Series of experiments were performed according to an empirical planning design based on the active central composite rotatable design of a 2³ order using an experimental matrix that considered the variation domain of each independent variable (X_i), their basic value (X_i0), specific variation step (ΔX_i), and specific planning order. The experimental results were processed using a specifically designed algorithm until the mathematical model proposal and its validation.

The mathematical model, expressed by the general relation 2 [19,20,21,22], was found after the processing of all experimental results based on the least-square fitting model obtained in the experimental design points according to a statistical formula and rules for model coefficients’ calculation and their significance analysis (i.e., by the Student t-test) for a certain significance level (p = 0.05) and degree of freedom (ν₁ = n − 1 = 19 and ν₂= k − 1) [19,20,21].

Y = b₀ + ∑b_iX_i + ∑b_iiX_i² + ∑b_ijX_iX_j

(2)

where Y represents the decision/response function (dependent variable); X_i, X_j, X_ii, and X_ij are the coded independent variables of the ‘passive’ biosorption-based treatment system, and b₀, b_i, b_ii and b_ij are the model coefficients (i, j = 1, 2, 3).

In all ‘passive’ biosorption experiments, the values (levels) were attributed to each independent variable X_i in accordance with its basic value (Xi₀) and imposed variation step (ΔX_i0) corresponding to the coded variable values, i.e., X_i = 0, ±1, or α = ±1.682. The Fisher constant (F), multiple correlation coefficient (R_Yx1x2x3), or Fisher test (F_C), defined by well-known statistic relations, were calculated to establish the significance of all independent variable vs. experimental errors (F), the correlation between the experimental values (Y_e) and those calculated with the proposed model (Y_c) (R_YX1X2X3, F_c), meaning by an appropriate analysis of variance [19,20,21]. The mean standard deviation between the experimental and model-based calculated data of dye removals must correspond to a good accordance, i.e., mean standard deviation value in the range of −10% to +10%.

For the proposed mathematical model, the determination of the maximum value of the response/decision function (dependent variable) and the corresponding value of each independent variable was permitted, i.e., Y* = max f(X₁*,X₂*,X₃*)—the maximum O16 dye removal by ‘passive’ biosorption onto the prepared immobilized biosorbent by using the classical optimization methodology. Graphical representations (3D surface and 2D contour) of the decision/response function (Y) variation vs. two or one independent variables (X_i and X_j, or only X_i, i,j = 1–3) were illustrated using WinSurf and Excel.

3. Results

3.1. ‘Pasive’ Biosorption Performance in Anionic Orange 16 Dye Removal

From our experimental results, the anionic O16 reactive dye biosorption onto prepared biosorbent based on the residual biomass of the Lactobacillus sp. mixture immobilized in sodium alginate was dependent on a few influencing factors and its biosorptive characteristics (i.e., adequate dye ‘passive’ biosorption isotherm—Langmuir II model; thermodynamic and kinetic aspects—type 2 order; action mechanism—predominantly physical due to its calculated active energy value) and performances (i.e., dye removal efficiencies and highest dye biosorption capacities), which were preliminarily reported in our previous research [12,26]. From these reported findings, the adequate experimental variation field for each independent variable was established and used in the present study to obtain high O16 dye removal efficiencies (>50–70%) and biosorption capacities (i.e., q > 60–100 mg of dye/g biosorbent) [12]. For very good experimental biosorption results and laboratory simulations, a few operational working conditions must be kept constant, such as pH 2, anionic O16 reactive dye concentration (89.76 mg dye/L), and spherical granule size of prepared biosorbent (1–1.5 mm), which were experimentally found and considered by us to be the best corresponding values for the highest amount of retained dye onto the tested immobilized biosorbent (values found in our reported data) [12]. All ‘passive’ biosorption experiments were performed according to the experimental planning matrix with given values of each independent variable (X_i) according to the active central compositional rotatable design of a 2³ order.

In our previous paper, it was concluded that the ‘passive’ biosorption process mechanism of the O16 dye onto immobilized biosorbent based on a residual Lactobacillus sp. biomass mixture is spontaneous (ΔG° = −1.845 ÷ (−1.768) kJ/mol) and exothermic (ΔH° = −6.512 kJ/mol), and predominantly of physical nature (based on physical bonding established between the charged surface sites of biosorbent and the functional groups of anionic O16 reactive dye due to predominant hydrogen bonds, hydrophobic bonds, Van der Waals bonds, dipole and steric effects, etc., i.e., physical forces: 4–10 kJ/mol for Van der Waals bonding, 5 kJ/mol—hydrophobic bonding, 40 kJ/mol—coordination bonding, 2–29 KJ/mol—dipole bonding, and for chemical forces—>60 kJ/mol [27,28]). These values were adequately described by a Langmuir II isotherm and associated with values of ‘passive’ biosorption energy (E) in the range of 11.471–13.867 KJ/mol [12].

Some experimental data concerning the performance in terms of dye removal efficiency and biosorption capacity working in the static batch regime are shown in Figure 2a,b after a S/W contact duration of 24 h (always ‘passive’ biosorption equilibrium attained). Other experimental reference data were reported in previous research works, in which the retaining of the anionic O16 dye into the molecular structure of prepared immobilized biosorbent was demonstrated by advanced analytical analysis (SEM, FTIR-EDX) [12].

In the present experimental planning design of O16 dye biosorption, all experiments were tested for the aqueous solution with an 89.76 mg/L O16 dye concentration at pH 2 and varying biosorption contact time of more than 4 h till 24 h, where very good results were preliminarily performed for anionic O16 dye removal onto residual immobilized biomass according to the calculated ‘passive’ biosorption capacity value and its dye removal efficiency. Thus, the maximum O16 dye biosorption capacities calculated with the Langmuir I model, working with a dye-containing solution of 89.76 mg of O16 dye/L, meaning 227.273 mg/g, or 185.185 mg/g, was performed for the biosorbent concentrations in the range of 10–13 g/L at 48 °C and 25 °C, respectively.

Additional processed experimental data are illustrated in Figure 2, which show a lower immobilized biosorbent concentration of 4 g/L for the same case of an aqueous system containing 89.76 mg/L anionic O16 dye (Figure 2a), or different concentrations in the chosen variation range of 28.96–231.68 mg of dye/L (Figure 2b).

As shown in Figure 2a, for the initial dye concentration of 132.25 mg/L and immobilized biosorbent concentration of 4 g/L (around 5% dry weight), the dye biosorption capacity varied in the range of 36.33–94.24 mg/g, and for dye removal efficiency, the variation interval was of 21.98–57.01%; for entire temperature interval of 5–40 °C, the best results being obtained at the highest temperature value.

In static ‘passive’ biosorption working regime at pH 2 with 4 g/L of immobilized biosorbent, after the S/L phases contact period of 24 h, it seems that higher O16 dye biosorption capacities (>76.23 mg/g) were performed in the case of high dye content in an aqueous solution (>83.12 mg/L dye) at the highest tested temperature of 48 °C (Figure 2b), but the highest anionic O16 dye removal from aqueous solution was obtained for dye concentrations in the range of 50–100 mg/L dye, meaning the value of the 83.12 mg/L dye shown in Figure 2b at the highest applied temperature of 48 °C.

Therefore, our further ‘passive’ biosorption experiments according to the chosen empirical, experimental design were performed with aqueous solutions containing 89.76 mg/L O16 dye (ease preparation by dilution with a certain amount of dye stock solution in a flask of 25 mL) at pH 2 with varying concentrations of prepared immobilized biosorbent (2.92–13 g/L), varying temperature (5–48 °C, no more than 50 °C for easily controlling the possible residual biomass degradation) and biosorption duration (4–24 h).

3.2. Empirical Experimental Modeling Data

For the three studied independent variables with significance into the ‘passive’ biosorption of O16 dye onto prepared immobilized biosorbent, the experimental variation fields and their real starting (basic) values (Z_i0) were established with real variation steps (∆Z_i0) corresponding to coded values (X_i), as shown in

Table 1. Established variation field of independent variables (real value, variation step, and attributed coded variable) in the active central compositional rotatable design of a 2³ order for anionic O16 reactive dye ‘passive’ biosorption onto prepared immobilized biosorbent.

Independent Variable (Measurement Units)	Real Variable (Zi)	Real Basal Variable Value (Zi0)	Variation Step of Real Variable (∆Zi0)	Coded Variable (Xi)
Biosorbent concentration (g/L)	Z1	8	3	X1
Temperature (°C)	Z2	25	10	X2
Biosorption time (h)	Z3	14	6	X3

and

Table 2. Experimental planning matrix according to the active central compositional rotatable design of 2³ orders for static O16 dye biosorption onto prepared immobilized biosorbent (residual Lactobacillus sp. biomass immobilized in sodium alginate).

Exp. No.	Z1, (g/L)	Z2, (°C)	Z3, (h)	X1	X2	X3	Yei (%)	Yci (%)	Standard Deviation (A)
1	5	15	8	−1	−1	−1	6.88	5.143	0.252
2	11	15	8	1	−1	−1	20.44	19.867	0.031
3	5	35	8	−1	1	−1	10.298	17.423	−0.692
4	11	35	8	1	1	−1	26.59	20.623	0.224
5	5	15	20	−1	−1	1	32.16	32.121	0.001
6	11	15	20	1	−1	1	79.98	66.849	0.164
7	5	35	20	−1	1	1	15.08	9.705	0.356
8	11	35	20	1	1	1	37.24	32.969	0.115
9	3	15	14	−1.682	0	0	4.807	1.924	0.599
10	13	15	14	1.682	0	0	22.44	33.821	−0.507
11	8	35	14	0	−1.682	0	38.44	44.816	−0.165
12	8	35	14	0	1.682	0	24.49	26.690	−0.088
13	8	25	4	0	0	−1.682	8.22	6.045	0.265
14	8	25	24	0	0	1.682	28.44	39.116	−0.375
15	8	8	14	0	0	0	21.47	22.337	−0.040
16	8	42	14	0	0	0	23.88	22.337	0.065
17	8	25	14	0	0	0	21.14	22.337	−0.023
18	8	25	14	0	0	0	22.35	22.337	0.001
19	8	25	14	0	0	0	23.11	22.337	0.033
20	8	25	14	0	0	0	22.86	22.337	0.023

.

Samples of 25 mL of the anionic O16 dye solution (89.76 mg of dye/L) were contacted with different contents of the prepared immobilized biosorbent at pH 2 under initial continuous stirring (30 rpm) of 1–3 min, at a different temperature (5–48 °C) and analyzed after a specific contact time (t_biosorption, [h]) for finding the remaining O16 dye concentration in the aqueous solution, and consequently, the O16 dye removal efficiency (%) according to the experimental planning design (Table 2).

The experimental data processing permitted the proposal of a mathematical model for the anionic O16 dye biosorption onto prepared immobilized biosorbent, which was considered a dependent variable—O16 dye removal from aqueous solution (Y, %) and is shown as follows:

Y = 22.337 + 9.482X₁ − 5.400X₂ + 9.831X₃ − 1.578X₁² + 4.735X₂² + 0.086X₃² − 2.866X₁X₂ + 5.016X₁X₃ − 8.674X₂X₃

(3)

All mathematical model coefficients were calculated with known statistical relations reported in other authors’ works [19,20], and the significance of each model coefficient was analyzed by application of the Student’s t-test. According to the Student’s t-test, the X₃² term is insignificant and, thus, the proposed model can be simplified as follows (4).

Y = 22.337 + 9.482X₁ − 5.400X₂ + 9.831X₃ − 1.578X₁² + 4.735X₂² − 2.866X₁X₂ + 5.016X₁X₃ − 8.674X₂X₃

(4)

Correlations between the experimental and calculated data with the proposed mathematical model are presented in Table 2 for O16 dye biosorption onto tested biosorbent.

Analyzing the correlations between the experimental and calculated values of dye removal (Y, %) when using the proposed mathematical model must include these essential aspects:

−

The calculated value of the Fisher constant was F = 4712.711 for Y (O16 dye removal onto prepared immobilized biosorbent) related to the statistic value (from the statistical table), which was of F_tab = 4.60 (for α = 99, ν₁ = n − 1 = 19, ν₂ = k − 1 = 2, where n is the number of experiments (n = 20), and k is the number of independent variables (k = 3)). Thus, F > F_tab, indicating that the deviation of experimental data (Y_ei) related to the mean value of all experimental values ($\stackrel{-}{Ye}$_i) are caused by the effects of independent variables (X_i) against the dependent variable (Y) considered as a decision/response function, and not caused by the experimental errors.

−

The calculated value of the multiple correlation coefficient was found to be R_YX1X2X3 = 0.9339 for the O16 dye removal onto the prepared immobilized biosorbent (Y), which was close to the unity value. This closed-to-unity value indicates that all three independent variables (X_i) had significant importance on the variation and possibility of the control of the dependent variable (anionic O16 dye removal), which was considered as a decision/response function in the chosen experimental variation field of each independent variable (real Z_i variable or coded X_i variable).

−

The calculated Fisher test value was F_C = 36.4002 for Y (O16 dye removal onto the prepared immobilized biosorbent), which is higher with more than 5.524 times than the statistical value (from the table) of F_C,tab = 6.59 for the freedom degree of ν₁ = n− k − 1 = 16 and ν₂ = k = 3 (where, k—number of independent variables). Thus, it has been demonstrated that the independent variables (X_i) had a significant influence on the Y—y-decision/response function (O16 dye biosorption efficiency). In addition, for the case of a proposed mathematical model, the dispersion of experimental data was 0.77635 for Y, and the dispersion of proposed model coefficients was calculated at 0.0388.

−

After processing the experimental data, an acceptable correlation between the experimental (Y_ei) and calculated (Y_ci) values of O16 dye removals was found that corresponded to a mean/average deviation of +1.1962%, situated into the admissible limitation range of −10% ÷ (+10%).

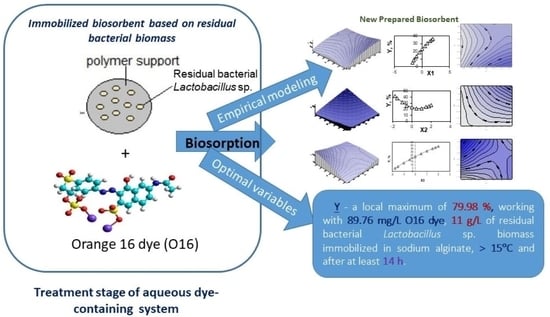
As shown in the experimental planning matrix (Table 2), it can be considered that a local maximum value (Y* = 79.98%) exists in the chosen experimental variation field of all independent variables, corresponding to coded values of X₁* = +1.0, X₂* = +1.0 and X₃* = +1.0, and respectively, an immobilized biosorbent concentration of 11 g/L (0.275 g per 25 mL sample, corresponding to 0.0139 g dry weight (d.w.) biosorbent per 25 mL)), a biosorption temperature of 15 °C, and a biosorption duration of 20 h.

These data are adequate only in the case of ‘passive’ biosorption using the prepared immobilized biosorbent (based on residual Lactobacillus sp. biomass) applied for an aqueous sample containing 89.76 mg of O16 dye/L, commonly in the range of 50–100 mg/L.

Figure 3a–f illustrates the effect of two independent variables (one independent variable kept constant at the basic coded value) against the anionic O16 dye removal (Y) (i.e., Y = Y(X₁,X₂,0), Y = Y(X₁,0,X₃) and Y = Y(0,X₂,X₃)).

The effect of each independent variable against the anionic O16 dye removal (Y) when two independent variables (X_i) are kept constant at their basic values is illustrated in Figure 4a–c (i.e., Y = Y (X₁,0,0), Y = Y(0,X₂,0) and Y = Y(0,0,X₃)).

4. Discussion

The analysis of the response function (Y) indicates that all independent X_i variables (immobilized biosorbent concentration, biosorption temperature, and contact time/biosorption duration working in a static regime) had significant effects against the anionic O16 reactive dye removal efficiency, a fact indicated by the higher values than unity of the coefficients of X₁, X₂, and X₃ terms.

The effect of the independent X₃ variable (static biosorption duration) on O16 dye removal from aqueous solution (Y decision/response function) is quite like that of X₁ (immobilized biosorbent concentration) (i.e., X₃ effect is 1.0368 times higher than that of X₁) and their effects are similar on Y (i.e., increasing of immobilized biosorbent concentration—X₁ and biosorption contact time—X₃ will increase O16 dye removal efficiency).

The effect of X₃ variable (static biosorption duration) on the Y response function (O16 dye removal) is almost two times higher (exactly 1.8206 times) than that of X₂ (biosorption temperature), and their effects are opposite (i.e., the increasing of static biosorption duration—X₃ decreases the required biosorption temperature—X₂ for obtaining of the wanted O16 dye removal from the aqueous sample, or decreasing of static biosorption duration imposed increasing of temperature till maximum acceptable value for controlled increasing dye removal efficiency).

The effect of the X₁ variable (immobilized biosorbent concentration) on the Y response function (O16 dye removal) is almost two times higher (exactly 1.7559 times higher) than that of X₂ (biosorption temperature), and their effects are opposite (i.e., the increasing of immobilized biosorbent concentration—X₁ and decreasing of biosorption temperature—X₂ increases O16 dye removal efficiency, or decreasing of immobilized biosorbent concentration and increasing of biosorption temperature may decrease the dye removal efficiency, in acceptable variation range of all three independent variables).

Further application of classical maximization methodology of Y response function (i.e., Y* = f(X₁*,X₂*,X₃*)), which consisted of resolving the first- and second-order derivates equation systems, concluded that the Y* decision/response function (maximum O16 dye removal by ‘passive’ biosorption on the prepared immobilized biosorbent) had no distinct maximum. However, a local maximum value (79.98%) can be mentioned, which was experimentally found as corresponding to X₁* = +1.00, X₂* = −1.00 and X₃* = +1.00, respectively, to 11 g/L biosorbent at a temperature of 15 °C and 20 h of static biosorption for the aqueous solutions containing an initial concentration of 89.76 mg/L anionic O16 dye.

The graphical representations of the O16 dye removal variation (Y, %) in the experimental field of two independent variables (on isoline) (i.e., Figure 3a–f) indicate the following aspects:

(1)

The immobilized biosorbent concentration (X₁) had one of the high levels of significance in performing high O16 dye removal, thus requiring coded values higher than the basic (X₁ > 0) where the local maximum O16 dye removal was no more than 45% (working at 35 °C for 14 h). It seems that the increase in the immobilized biosorbent concentration increases the O16 dye removal efficiency (Figure 3a–b).

(2)

A static biosorption duration higher than 8 h (as a possible shift at work) was beneficial, and the best results (e.g., O16 dye removals higher than 60%) were obtained after at least 20 h (Figure 3c,d);

(3)

Maximum experimental values of O16 dye removal (Y > 70%) were obtained when working at the sorption temperature of 15 °C (or smaller) and 20 h (or greater) on aqueous samples with an 89.76 mg/L initial dye concentration (Figured 3e,f) (i.e., the experimental Y value of 79.98% performed at 15 °C after 20 h).

(4)

If the operating biosorption regime is discontinuous, higher values of O16 dye removal can be performed after a biosorption duration greater than 20 h (as found in previous authors’ work—after 24 h) [12].

The graphical representations (Figure 3) allowed us to illustrate the 3D (surface) and 2D (contour) variation of the Y-response/decision function; its maximum values in the selected experimental field on isolines (2D) were obtained when one independent variable was constantly kept at their basic value.

When two independent variables (X_i) are kept constant at their basic values (X_i,j = 0), additional information may be underlined as follows:

−

The effect of the X₁ variable (initial immobilized biosorbent concentration) viz. Y is illustrated in Figure 4a. It seems there is no distinct maximum but only an extreme local maximum value for O16 dye removal (Y* = 34.985%) at X₁* = +2.00 corresponding to an immobilized biosorbent concentration of 16 g/L for an anionic dye concentration of 89.76 mg/L, biosorption temperature of 25 °C and biosorption duration of 14 h (X₂ and X₃ kept constant at their basic values). The X₁ variable (immobilized biosorbent concentration) had a significant effect on the maximum value of Y*.

−

The effect of X₂ variable (biosorption temperature) (coded X₁ and X₃ values are equal with 0) viz. O16 dye removal (Y) indicates the existence of a distinct minimum of dye removal (20.821%); thus, an extreme local maximum can be considered (Y = 52.776%) at X₂* = −2.00, corresponding to a biosorption temperature of 5 °C, immobilized biosorbent concentration of 8 g/L and biosorption duration of 14 h (Figure 4b).

−

The effect of the X₃ variable (biosorption time/duration) (coded X₁ and X₂ values are kept equal with 0) viz. anionic O16 dye removal (Y) indicates no distinct maximum dye removal, thus only an extreme local maximum can be considered (Y = 42.343%) for X₃* = +2.00, i.e., a biosorption duration of 28 h, a temperature of 25 °C and an immobilized biosorbent concentration of 8 g/L (Figure 4c). The X₃ variable (biosorption duration) had the most significant influence on the Y-value in association with the immobilized biosorbent concentration (X₁).

Considering the two independent variables at their basic values, we can conclude that the optimum values of the O16 dye removal efficiency (Y*) using static ‘passive’ biosorption on a prepared immobilized biosorbent based on residual Lactobacillus sp. consortium biomass corresponded to a relatively high concentration of biosorbent (more than 11 g/L, or >0.50 g biosorbent per 25 mL of the sample) working at nearly a winter room temperature in the case of an anionic dye-adsorptive biomaterial (i.e., >15 °C) for more than 14 h of biosorption time/duration.

The optimal dye removal corresponded to a local maximum value experimentally found, i.e., Y* = 79.98%. We performed similar external tests working at adjusted pH of 2 ± 0.5 with a concentration of immobilized biosorbent of around 11 g/L (5% dry weight) at a temperature of 15 ± 3 °C for 20 h for an industrial effluent (remaining wastewater from a rinsing step of final printed product) containing around 80 ± 5 mg/L O16 dye, and we obtained similar results, meaning dye removal of Y* = 75 ± 5.5%.

WinSurf and Excel were used in all experimental data processing and model validation.

5. Conclusions

The static ‘passive’ biosorption onto a newly prepared biosorbent based on residual Lactobacillus sp. biomass immobilized in sodium alginate represents a good alternative to Orange 16 dye removal from aqueous systems.

An empirical model was proposed by an active central compositional rotatable design of a 2³ order considering the immobilized biosorbent concentration (X₁), temperature (X₂) and static biosorption time/duration (X₃) as independent variables and the anionic O16 dye removal as the decision/response function (Y, %). The maximum values of the response/decision function (Y) were determined using the classical optimization methodology, and correlations between the experimental and model-based calculated data were appreciated by specific statistical indicators, i.e., Fisher constant (F), Fisher test (Fc), multiple correlation coefficient (R_Yx1x2x3), Student’s t-test, experimental data dispersion, and coefficients’ dispersion, standard deviation, etc.

The Y decision function was found to have no distinct maximum but only a local maximum of 79.98% when working with 11 g/L of prepared immobilized biosorbent (based on residual Lactobacillus sp. biomass) at 15 °C for 20 h in the case of 89.76 mg/L dye-containing treated samples.

The graphical representation of the O16 dye removal towards one or two selected independent variables permits the finding of the optimum variation field for each studied variable. The maximum solutions are encouraging (anionic O16 reactive dye removal > 66.849% onto prepared immobilized Lactobacillus sp.-based biosorbent) and allow us to continue with improvements of the process modeling and further optimization studies.