Arsenic Sulfide Suspended-core Fiber Simulation with Three Parabolic Air Holes for Supercontinuum Generation
Abstract
:1. Introduction
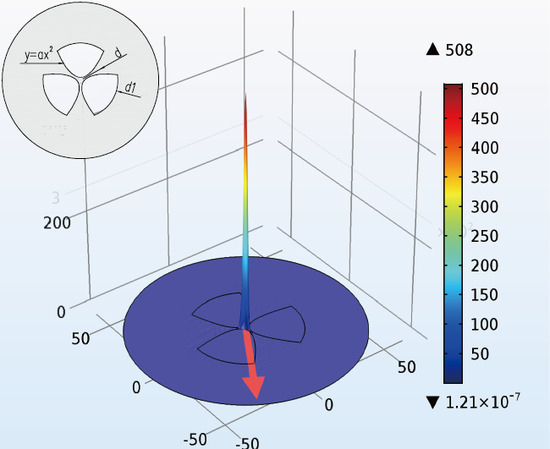
2. Structure Design
3. Characteristics Analysis
3.1. Effective Refractive Index
3.2. Nonlinear Coefficient
3.3. Chromatic Dispersion
3.4. Supercontinuum
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Poudel, C.; Kaminski, C.F. Supercontinuum radiation in fluorescence microscopy and biomedical imaging applications. J. Opt. Soc. Am. B 2019, 36, A139–A153. [Google Scholar] [CrossRef]
- Kano, H.; Hamaguchi, H.-O. In-vivo multi-nonlinear optical imaging of a living cell using a supercontinuum light source generated from a photonic crystal fiber. Opt. Express 2006, 14, 2798–2804. [Google Scholar] [CrossRef] [PubMed]
- Murugkar, S.; Brideau, C.; Ridsdale, A.; Naji, M.; Stys, P.K.; Anis, H. Coherent anti-Stokes Raman scattering microscopy using photonic crystal fiber with two closely lying zero dispersion wavelengths. Opt. Express 2007, 15, 14028–14037. [Google Scholar] [CrossRef] [PubMed]
- Monro, T.; Ebendorff-Heidepriem, H.; Schartner, E.; Warren-Smith, S. Sensing in suspended-core optical fibers. Proc. IEEE Winter Top. 2011, 159–160. [Google Scholar] [CrossRef]
- Bravo, M.; Fernández-Vallejo, M.; Echapare, M.; López-Amo, M.; Kobelke, J.; Schuster, K. Multiplexing of six micro-displacement suspended-core Sagnac interferometer sensors with a Raman-Erbium fiber laser. Opt. Express 2013, 21, 2971–2977. [Google Scholar] [CrossRef] [Green Version]
- Xuan, K.D.; Van, L.C.; Long, V.C.; Dinh, Q.H.; Xuan, L.V.; Trippenbach, M.; Buczynski, R. Dispersion characteristics of a suspended-core optical fiber infiltrated with water. Appl. Opt. 2017, 56, 1012–1019. [Google Scholar] [CrossRef]
- Russell, P. Photonic crystal fibers. Science 2003, 299, 358–362. [Google Scholar] [CrossRef]
- Knight, J.C. Photonic crystal fibres. Nature 2003, 424, 847–851. [Google Scholar] [CrossRef]
- Dong, L.; Thomas, B.K.; Fu, L. Highly nonlinear silica suspended core fibers. Opt Express 2008, 16, 16423–16430. [Google Scholar] [CrossRef]
- Yakasai, I.; Abas, P.E.; Kaijage, S.F.; Caesarendra, W.; Begum, F. Proposal for a Quad-Elliptical Photonic Crystal Fiber for Terahertz Wave Guidance and Sensing Chemical Warfare Liquids. Photonics 2019, 6, 78. [Google Scholar] [CrossRef] [Green Version]
- Price, J.H.V.; Monro, T.M.; Ebendorff-Heidepriem, H.; Poletti, F.; Horak, P.; Finazzi, V.; Leong, J.Y.Y.; Petropoulos, P.; Flanagan, J.C.; Brambilla, G.; et al. Mid-IR Supercontinuum Generation From Nonsilica Microstructured Optical Fibers. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 738–749. [Google Scholar] [CrossRef] [Green Version]
- Jiao, K.; Yao, J.; Wang, X.-G.; Wang, X.; Zhao, Z.; Zhang, B.; Si, N.; Liu, J.; Shen, X.; Zhang, P.; et al. 1.2–15.2 μm supercontinuum generation in a low-loss chalcohalide fiber pumped at a deep anomalous-dispersion region. Opt. Lett. 2019, 44, 5545–5548. [Google Scholar] [CrossRef]
- Tao, G.; Ebendorff-Heidepriem, H.; Stolyarov, A.M.; Danto, S.; Badding, J.V.; Fink, Y.; Ballato, J.; Abouraddy, A.F. Infrared fibers. Adv. Opt. Photonics 2015, 7, 379. [Google Scholar] [CrossRef]
- El-Amraoui, M.; Gadret, G.; Jules, J.C.; Fatome, J.; Fortier, C.; Désévédavy, F.; Skripatchev, I.; Messaddeq, Y.; Troles, J.; Brilland, L.; et al. Microstructured chalcogenide optical fibers from As2S3 glass: Towards new IR broadband sources. Opt. Express 2010, 18, 26655–26665. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mouawad, O.; Picot-Clémente, J.; Amrani, F.; Strutynski, C.; Smektala, F. 3.5-µm bandwidth mid-infrared supercontinuum generation in a 2-cm long suspended-core chalcogenide fiber. In Proceedings of the Specialty Optical Fibers, Barcelona, Spain, 27–31 July 2014; ISBN 978-1-55752-820-9. [Google Scholar] [CrossRef]
- Gao, W.; El Amraoui, M.; Liao, M.; Kawashima, H.; Duan, Z.; Deng, D.; Cheng, T.; Suzuki, T.; Messaddeq, Y.; Ohishi, Y. Mid-infrared supercontinuum generation in a suspended-core As2S3 chalcogenide microstructured optical fiber. Opt. Express 2013, 21, 9573–9583. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mouawad, O.; Kedenburg, S.; Steinle, T.; Steinmann, A.; Kibler, B.; Désévédavy, F.; Gadret, G.; Jules, J.-C.; Giessen, H.; Smektala, F. Experimental long-term survey of mid-infrared supercontinuum source based on As2S3 suspended-core fibers. Appl. Phys. B Lasers Opt. 2016, 122, 177. [Google Scholar] [CrossRef]
- Xue, Z.; Liu, S.; Zhao, Z.; Mi, N.; Wu, B.; Li, X.; Zhang, P.; Wang, X. Infrared Suspended-Core Fiber Fabrication Based on Stacked Chalcogenide Glass Extrusion. J. Lightwave Technol. 2018, 36, 2416–2421. [Google Scholar] [CrossRef]
- Gao, W.; Duan, Z.; Asano, K.; Cheng, T.; Deng, D.; Matsumoto, M.; Misumi, T.; Suzuki, T.; Ohishi, Y. Mid-infrared supercontinuum generation in a four-hole As2S5 chalcogenide microstructured optical fiber. Appl. Phys. B 2014, 116, 847–853. [Google Scholar] [CrossRef]
- Ebendorff-Heidepriem, H.; Warren-Smith, S.C.; Monro, T.M. Suspended nanowires: Fabrication, design and characterization of fibers with nanoscale cores. Opt. Express 2009, 17, 2646–2657. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Ma, W.; Zhang, P.; Zhu, L.; Yang, D.; Wang, X.; Dai, S. Mid-Infrared Gas Detection Using a Chalcogenide Suspended-Core Fiber. J. Lightwave Technol. 2019, 37, 5193–5198. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, P.; Li, X.; Nie, Q.; Wang, R.; Sun, L.; Chen, P.; Xue, Z.; Wang, X.; Dai, S.; et al. Fabrication and Characterization of Three-hole As2S3 Suspended-Core Fibers Based on Robust Extrusion. IEEE Access 2018, 6, 41093–41098. [Google Scholar] [CrossRef]
- Gao, W.; Duan, Z.; Asano, K.; Cheng, T.; Deng, D.; Matsumoto, M.; Misumi, T.; Suzuki, T.; Ohishi, Y. Supercontinuum Generation in an As2S5 Chalcogenide Microstructured Optical Fiber. In Proceedings of the 2014 Conference on Lasers and Electro-Optics (CLEO)-Laser Science to Photonic Applications, San Jose, CA, USA, 8–13 June 2014; IEEE: San Jose, CA, USA, 2014; Volume 116. [Google Scholar]
- Cheng, T.; Kanou, Y.; Deng, D.; Xue, X.; Matsumoto, M.; Misumi, T.; Suzuki, T.; Ohishi, Y. Mid-infrared supercontinuum generation in an AsSe2-As2S5 hybrid microstructured optical fiber. In Proceedings of the 2014 5th International Conference on Optical Communication Systems (OPTICS), Vienna, Austria, 28–30 August 2014; pp. 1–6. [Google Scholar]
- Peng, T.; Xu, T.; Wang, X. Simulation Study on Dispersion Properties of As2S3 Three-Bridge Suspended-Core Fiber. IEEE Access 2017, 5, 17240–17245. [Google Scholar] [CrossRef]
- Duhant, M.; Renard, W.; Canat, G.; Nguyen, T.N.; Smektala, F.; Troles, J.; Coulombier, Q.; Toupin, P.; Brilland, L.; Bourdon, P.; et al. Fourth-order cascaded Raman shift in AsSe chalcogenide suspended-core fiber pumped at 2 μm. Opt. Lett. 2011, 36, 2859. [Google Scholar] [CrossRef]
- Anashkina, E.A.; Shiryaev, V.S.; Koptev, M.Y.; Stepanov, B.S.; Muravyev, S.V. Development of As-Se tapered suspended-core fibers for ultra-broadband mid-IR wavelength conversion. J. Non-Cryst. Solids 2018, 480, 43–50. [Google Scholar] [CrossRef]
- Coscelli, E.; Poli, F.; Li, J.; Cucinotta, A.; Selleri, S. Dispersion Engineering of Highly Nonlinear Chalcogenide Suspended-Core Fibers. IEEE Photonics J. 2015, 7, 1–8. [Google Scholar] [CrossRef]
- Rodney, W.; Malitson, I.; King, T. Refractive Index of Arsenic Trisulfide. JOSA 1958, 48, 633–635. [Google Scholar] [CrossRef]
- Knight, J.C.; Birks, T.A.; Russell, P.S.J.; Atkin, D.M. All-silica single-mode optical fiber with photonic crystal cladding: Errata. Opt. Lett. 1996, 21, 1547–1549. [Google Scholar] [CrossRef]
- Harrington, J.A. Infrared Fibers and their Applications; SPIE Press: Bellingham, WS, USA, 2004. [Google Scholar] [CrossRef]
- Chaudhari, C.; Suzuki, T.; Ohishi, Y. Design of Zero Chromatic Dispersion Chalcogenide As S Glass Nanofibers. IEEE/OSA J. Lightwave Technol. J. Lightwave Technol. 2009, 27, 2095–2099. [Google Scholar] [CrossRef]
- Dudley, J.; Genty, G.; Coen, S. Supercontinuum generation in photonic crystal fiber. Rev. Mod. Phys. 2006, 78, 1135. [Google Scholar] [CrossRef]
- Xiong, C.; Magi, E.; Luan, F.; Tuniz, A.; Dekker, S.; Sanghera, J.S.; Shaw, L.B.; Aggarwal, I.D.; Eggleton, B.J. Characterization of picosecond pulse nonlinear propagation in chalcogenide As2S3 fiber. Appl. Opt. 2009, 48, 5467–5474. [Google Scholar] [CrossRef]
- Cimpl, Z.; Kosek, F.; Husa, V.; Svoboda, J. Refractive index of arsenic trisulphide. Czechoslov. J. Phys. B 1981, 31, 1191–1194. [Google Scholar] [CrossRef]
- Yang, T.; Ding, C.; Guo, Y.J. A Highly Birefringent and Nonlinear AsSe2–As2S5 Photonic Crystal Fiber With Two Zero-Dispersion Wavelengths. IEEE Photonics J. 2019, 11, 1–7. [Google Scholar] [CrossRef]
- Petersen, C.R.; Møller, U.; Kubat, I.; Zhou, B.; Dupont, S.; Ramsay, J.; Benson, T.; Sujecki, S.; Abdel-Moneim, N.; Tang, Z.; et al. Mid-infrared supercontinuum covering the 1.4–13.3 μm molecular fingerprint region using ultra-high NA chalcogenide step-index fibre. Nat. Photonics 2014, 8, 830–834. [Google Scholar] [CrossRef]
- Du, T.; Li, Y.; Wang, K.; Cai, Z.; Xu, H.; Xu, B.; Mashinsky, V.M.; Luo, Z. 2.01–2.42 μm All-Fiber Femtosecond Raman Soliton Generation in a Heavily Germanium Doped Fiber. IEEE J. Sel. Top. Quantum Electron. 2019, 25, 1–7. [Google Scholar] [CrossRef]
- Huang, R.; Zhou, R.; Li, Q. Mid-Infrared Supercontinuum Generation in Chalcogenide Photonic Crystal Fibers with a Weak CW Trigger. J. Lightwave Technol. 2020, 38, 1522–1528. [Google Scholar] [CrossRef]
- Jiao, K.; Yao, J.; Zhao, Z.; Wang, X.; Si, N.; Wang, X.; Chen, P.; Xue, Z.; Tian, Y.; Zhang, B.; et al. Mid-infrared flattened supercontinuum generation in all-normal dispersion tellurium chalcogenide fiber. Opt. Express 2019, 27, 2036–2043. [Google Scholar] [CrossRef]
- Yang, L.; Li, Y.; Zhang, B.; Wu, T.; Zhao, Y.; Hou, J. 30-W supercontinuum generation based on ZBLAN fiber in an all-fiber configuration. Photonics Res. 2019, 7, 1061. [Google Scholar] [CrossRef]
- Diouf, M.; Mandeng, L.M.; Tchawoua, C.; Zghal, M. Numerical Investigation of Supercontinuum Generation Through AsSe2/As2S5 Chalcogenide Photonic Crystal Fibres and Rib Structures. J. Lightwave Technol. 2019, 37, 5692–5698. [Google Scholar] [CrossRef]
- Park, K.; Na, J.; Kim, J.; Jeong, Y. Numerical Study on Supercontinuum Generation in an Active Highly Nonlinear Photonic Crystal Fiber With Anomalous Dispersion. IEEE J. Quantum Electron. 2020, 56, 1–9. [Google Scholar] [CrossRef]














| Year/Ref. | Glass Components | Structure | Length | ZDW | Pump Wavelength | Pump Peak Power | FWHM | Spectral Bandwidth |
|---|---|---|---|---|---|---|---|---|
| Unit | cm | μm | μm | kW | fs | μm | ||
| 2013/[16] | As2S3 | 3-hole | 1.3/2.4 | 2.52 | 2.6 | 0.24–1.32 | ~200 | 1.520–4.610 |
| 2014/[15] | As2S3 | 3-hole | 2 | 2.5 | 2.5 | 1.25–4.86 | 200 | 0.6–4.1 |
| 2014/[23] | As2S5 | 4-hole | 4.8 | 2.28 | 2.3 | 0.22–1.55 | 200 | 1.370–5.650 |
| 2014/[24] | AsSe2-As2S5 | 4-hole | 2 | 3.38 | 3.389 | 1.356 | ~200 | 1.256–5.400 |
| 2016/[17] | As2S3 | 3-hole | 2.5 | 2.65 | 3.5 | 0.015 | 300 | 2.5–5.5 |
| 2018/[24] | As2S3-Ge20As20Se15Te45 | 4-hole | 19 | 3.93 | 4.5 | 66 | 150 | 2.06–6.95 |
| d = 1 μm | d = 3 μm | d = 5 μm | d = 9 μm | |
|---|---|---|---|---|
| Mean (μm) | 1.5336 | 2.0814 | 2.6860 | 4.5493 |
| Standard Deviation | 0.0243 | 0.0579 | 0.0687 | 0.1218 |
| β1 (fs/mm) | β2 (fs2/mm) | β3 (fs3/mm) | β4 (fs4/mm) | β5 (fs5/mm) | β6 (fs6/mm) | β7 (fs7/mm) | β8 (fs8/mm) | β9 (fs9/mm) | β10 (fs10/mm) |
|---|---|---|---|---|---|---|---|---|---|
| 5.3381× 105 | −6.73833× 10−16 | 1.31008× 10−27 | −4.6199× 10−42 | 2.39585× 10−56 | −4.6505× 10−71 | −2.43177× 10−85 | 5.22843× 10−99 | 5.21097× 10−112 | −7.83179× 10−124 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, T.; Wang, X.; Xu, T. Arsenic Sulfide Suspended-core Fiber Simulation with Three Parabolic Air Holes for Supercontinuum Generation. Photonics 2020, 7, 46. https://doi.org/10.3390/photonics7030046
Peng T, Wang X, Xu T. Arsenic Sulfide Suspended-core Fiber Simulation with Three Parabolic Air Holes for Supercontinuum Generation. Photonics. 2020; 7(3):46. https://doi.org/10.3390/photonics7030046
Chicago/Turabian StylePeng, Tao, Xunsi Wang, and Tiefeng Xu. 2020. "Arsenic Sulfide Suspended-core Fiber Simulation with Three Parabolic Air Holes for Supercontinuum Generation" Photonics 7, no. 3: 46. https://doi.org/10.3390/photonics7030046
APA StylePeng, T., Wang, X., & Xu, T. (2020). Arsenic Sulfide Suspended-core Fiber Simulation with Three Parabolic Air Holes for Supercontinuum Generation. Photonics, 7(3), 46. https://doi.org/10.3390/photonics7030046