Intensity and Coherence Characteristics of a Radial Phase-Locked Multi-Gaussian Schell-Model Vortex Beam Array in Atmospheric Turbulence
Abstract
:1. Introduction
2. Theory Analysis
2.1. Analytical Description of RPLMGSMV Beam Array
2.2. Propagation Analysis
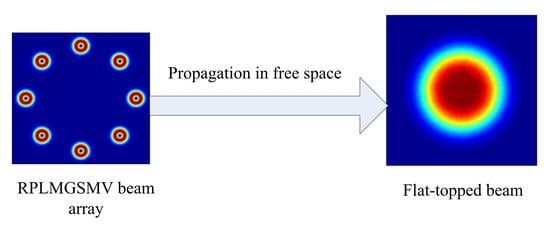
3. Numerical Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, F.; Liu, X.L.; Cai, Y.J. Propagation of partially coherent beam in turbulent atmosphere: A review. Prog. Electromagn. Res. 2015, 150, 123–143. [Google Scholar] [CrossRef] [Green Version]
- Peleg, A.; Moloney, J.V. Scintillation index for two Gaussian laser beams with different wavelengths in weak atmospheric turbulence. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2006, 23, 3114–3122. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, Y.P.; Zhao, G.P.; Gao, Z.H.; He, D. A comparative study of standard and elegant Hermite-Gaussian beams propagating through turbulent atmosphere. J. Mod. Opt. 2011, 58, 1239–1245. [Google Scholar] [CrossRef]
- Boufalah, F.; Dalil-Essakali, L.; Nebdi, H.; Belafhal, A. Effect of turbulent atmosphere on the on-axis average intensity of Pearcey–Gaussian beam. Chin. Phys. B 2016, 25, 064208. [Google Scholar] [CrossRef]
- Zhou, G.Q. Propagation of a radial phased-locked Lorentz beam array in turbulent atmosphere. Opt. Express 2011, 19, 24699–24711. [Google Scholar] [CrossRef]
- Tang, M.M.; Zhao, D.M. Regions of spreading of Gaussian array beams propagating through oceanic turbulence. Appl. Opt. 2015, 54, 3407–3411. [Google Scholar] [CrossRef]
- Lu, L.; Wang, Z.Q.; Zhang, J.H.; Zhang, P.F.; Qiao, C.H.; Fan, C.Y.; Ji, X.L. Average intensity of M x N Gaussian array beams in oceanic turbulence. Appl. Opt. 2015, 54, 7500–7507. [Google Scholar] [CrossRef]
- Liu, Z.; Wei, H.Y.; Cai, D.M.; Jia, P.; Zhang, R.; Li, Z.J. Spiral spectrum of Laguerre-Gaussian beams in slant non-Kolmogorov atmospheric turbulence. Optik 2017, 142, 103–108. [Google Scholar] [CrossRef]
- Yin, X.; Zhang, L.C. Quantum polarization fluctuations of an Airy beam in turbulent atmosphere in a slant path. J. Opt. Soc. Am. A 2016, 33, 1348–1352. [Google Scholar] [CrossRef]
- Dong, K.Y.; Dong, Y.; Song, Y.S.; Chang, S. The properties of anomalous hollow beam propagating in the slant atmosphere. Optik 2018, 172, 1040–1046. [Google Scholar] [CrossRef]
- Eyyuboğlu, H.T.; Cai, Y. Non-Kolmogorov spectrum scintillation aspects of dark hollow and flat topped beams. Opt. Commun. 2012, 285, 969–974. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, K.; Chen, Z.; Pu, J. Scintillation index of double vortex beams in turbulent atmosphere. Optik 2019, 181, 571–574. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, X.; Yuan, X. Performance analysis of sinh-Gaussian vortex beams propagation in turbulent atmosphere. Opt. Commun. 2019, 440, 100–105. [Google Scholar] [CrossRef]
- Huang, Y.; Yuan, Y.S.; Liu, X.L.; Zeng, J.; Wang, F.; Yu, J.Y.; Liu, L.; Cai, Y.J. Propagation of optical coherence vortex lattices in turbulent atmosphere. Appl. Sci. 2018, 8, 2476. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.C.; Yin, X.; Zhu, Y. Polarization fluctuations of partially coherent Hermite-Gaussian beams in a slant turbulent channel. Optik 2014, 125, 3272–3276. [Google Scholar] [CrossRef]
- Wang, D.; Wang, F.; Cai, Y.; Chen, J. Evolution properties of the complex degree of coherence of a partially coherent Laguerre–Gaussian beam in turbulent atmosphere. J. Mod. Opt. 2012, 59, 372–380. [Google Scholar] [CrossRef]
- Gao, M.; Gong, L.; Wu, P.L. Depolarization characteristics of incompletely polarized and partially coherent laser beams in slant atmospheric turbulence. Optik 2014, 125, 4860–4863. [Google Scholar] [CrossRef]
- Xu, Y.G.; Dan, Y.Q.; Zhang, B. Spreading and M-2-factor based on second-order moments for partially-coherent anomalous hollow beam in turbulent atmosphere. Optik 2016, 127, 4590–4595. [Google Scholar] [CrossRef]
- Wang, F.; Li, J.; Martinez-Piedra, G.; Korotkova, O. Propagation dynamics of partially coherent crescent-like optical beams in free space and turbulent atmosphere. Opt. Express 2017, 25, 26055–26066. [Google Scholar] [CrossRef]
- Yousefi, M.; Kashani, F.D.; Mashal, A. Analyzing the average intensity distribution and beam width evolution of phase-locked partially coherent radial flat-topped array laser beams in oceanic turbulence. Laser Phys. 2017, 27, 026202. [Google Scholar] [CrossRef]
- Kashani, F.D.; Yousefi, M. Analyzing the propagation behavior of coherence and polarization degrees of a phase-locked partially coherent radial flat-topped array laser beam in underwater turbulence. Appl. Opt. 2016, 55, 6311–6320. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.H.; Mei, Z.R.; Gu, J.G. Propagation of Gaussian Schell-model Array beams in free space and atmospheric turbulence. Opt. Laser Technol. 2016, 86, 14–20. [Google Scholar] [CrossRef]
- Liu, D.J.; Wang, Y.C.; Yin, H.M. Propagation properties of partially coherent four-petal Gaussian vortex beams in turbulent atmosphere. Opt. Laser Technol. 2016, 78, 95–100. [Google Scholar] [CrossRef]
- Mei, Z.; Tong, Z.; Korotkova, O. Electromagnetic non-uniformly correlated beams in turbulent atmosphere. Opt. Express 2012, 20, 26458–26463. [Google Scholar] [CrossRef]
- Korotkova, O.; Sahin, S.; Shchepakina, E. Multi-Gaussian Schell-model beams. J. Opt. Soc. Am. A 2012, 29, 2159–2164. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y. Properties of a random electromagnetic multi-Gaussian Schell-model vortex beam in oceanic turbulence. Appl. Phys. B 2018, 124, 176. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Zhong, H.; Wang, G.; Yin, H.; Dong, A. Properties of multi-Gaussian correlated partially coherent anomalous hollow beam propagating in underwater oceanic turbulence. Opt. Laser Technol. 2019, 119, 105604. [Google Scholar] [CrossRef]
- Liu, D.-J.; Wang, Y.-C.; Wang, G.-Q.; Yin, H.-M.; Zhong, H.-Y. Properties of multi-Gaussian Schell-model beams carrying an edge dislocation propagating in oceanic turbulence. Chin. Phys. B 2019, 28, 104207. [Google Scholar] [CrossRef]
- Xu, H.F.; Zhang, Z.; Qu, J.; Huang, W. Propagation factors of cosine-Gaussian-correlated Schell-model beams in non-Kolmogorov turbulence. Opt. Express 2014, 22, 22479–22489. [Google Scholar] [CrossRef]
- Zhu, J.; Li, X.; Tang, H.; Zhu, K. Propagation of multi-cosine-Laguerre-Gaussian correlated Schell-model beams in free space and atmospheric turbulence. Opt. Express 2017, 25, 20071–20086. [Google Scholar] [CrossRef]
- Liu, D.; Zhong, H.; Wang, G.; Yin, H.; Wang, Y. Radial phased-locked multi-Gaussian Schell-model beam array and its properties in oceanic turbulence. Opt. Laser Technol. 2020, 124, 106003. [Google Scholar] [CrossRef]
- Ma, X.; Liu, D.; Wang, Y.; Yin, H.; Zhong, H.; Wang, G. Propagation of Rectangular Multi-Gaussian Schell-Model Array Beams through Free Space and Non-Kolmogorov Turbulence. Appl. Sci. 2020, 10, 450. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.T.; Liu, L.; Zhao, C.L.; Cai, Y.J. Multi-Gaussian Schell-model vortex beam. Phys. Lett. A 2014, 378, 750–754. [Google Scholar] [CrossRef]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]
- Jeffrey, A.; Dai, H.H. Handbook of Mathematical Formulas and Integrals, 4th ed.; Academic Press Inc.: Cambridge, MA, USA, 2008. [Google Scholar]










Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Wang, G.; Ma, X.; Zhong, H.; Yin, H.; Wang, Y.; Liu, D. Intensity and Coherence Characteristics of a Radial Phase-Locked Multi-Gaussian Schell-Model Vortex Beam Array in Atmospheric Turbulence. Photonics 2021, 8, 5. https://doi.org/10.3390/photonics8010005
Zhao J, Wang G, Ma X, Zhong H, Yin H, Wang Y, Liu D. Intensity and Coherence Characteristics of a Radial Phase-Locked Multi-Gaussian Schell-Model Vortex Beam Array in Atmospheric Turbulence. Photonics. 2021; 8(1):5. https://doi.org/10.3390/photonics8010005
Chicago/Turabian StyleZhao, Jialu, Guiqiu Wang, Xiaolu Ma, Haiyang Zhong, Hongming Yin, Yaochuan Wang, and Dajun Liu. 2021. "Intensity and Coherence Characteristics of a Radial Phase-Locked Multi-Gaussian Schell-Model Vortex Beam Array in Atmospheric Turbulence" Photonics 8, no. 1: 5. https://doi.org/10.3390/photonics8010005
APA StyleZhao, J., Wang, G., Ma, X., Zhong, H., Yin, H., Wang, Y., & Liu, D. (2021). Intensity and Coherence Characteristics of a Radial Phase-Locked Multi-Gaussian Schell-Model Vortex Beam Array in Atmospheric Turbulence. Photonics, 8(1), 5. https://doi.org/10.3390/photonics8010005