Optical Characterization of Ultra-Thin Films of Azo-Dye-Doped Polymers Using Ellipsometry and Surface Plasmon Resonance Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. UV-Visible Spectroscopy
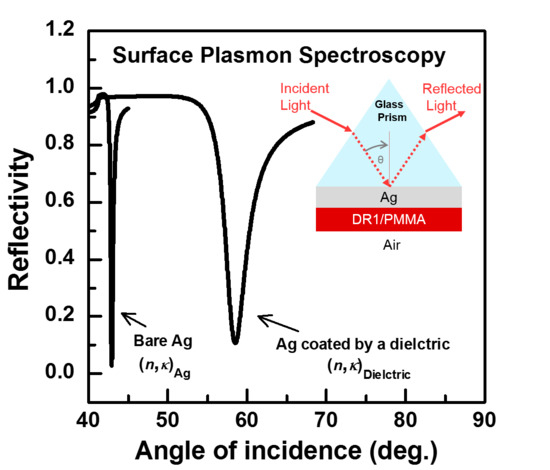
3.2. SPR Spectroscopy
3.3. Spectroscopic Ellipsometry
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sekkat, Z.; Wood, J.; Geerts, Y.; Knoll, W. Surface Plasmon Investigations of Light-Induced Modulation in the Optical Thickness of Molecularly Thin Photochromic Layers. Langmuir 1996, 12, 2976–2980. [Google Scholar] [CrossRef]
- Bartual-Murgui, C.; Salmon, L.; Akou, A.; Thibault, C.; Molnár, G.; Mahfoud, T.; Sekkat, Z.; Real, J.A.; Bousseksou, A. High quality nano-patterned thin films of the coordination compound {Fe(pyrazine)[Pt(CN)4]} deposited layer-by-layer. New J. Chem. 2011, 35, 2089–2094. [Google Scholar] [CrossRef]
- Shah, D.; Reddy, H.; Kinsey, N.; Shalaev, V.M.; Boltasseva, A. Optical Properties of Plasmonic Ultrathin TiN Films. Adv. Opt. Mater. 2017, 5, 1700065. [Google Scholar] [CrossRef]
- Huang, H.T.; Huang, C.Y.; Ger, T.R.; Wei, Z.H. Anti-integrin and integrin detection using the heat dissipation of surface plasmon resonance. Appl. Phys. Lett. 2013, 102, 111109. [Google Scholar] [CrossRef]
- Krasilnikova, S.A. Measurement of optical constants of thin films by non conventional ellipsometry, photothermal deflection spectroscopy and plasmon resonance spectroscopy. In Proceedings of the Advances in Optical Thin Films III, 71010R, Glasgow, Scotland, UK, 2–5 September 2008; Volume 7101. [Google Scholar] [CrossRef]
- Wood, R.W. On a Remarkable Case of Uneven Distribution of Light in a Diffraction Grating Spectrum. Proc. Phys. Soc. Lond. 1902, 18, 269–275. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- Nguyen, H.; Park, J.; Kang, S.; Kim, M. Surface Plasmon Resonance: A Versatile Technique for Biosensor Applications. Sensors 2015, 15, 10481–10510. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brolo, A.G. Plasmonics for future biosensors. Nat. Photon. 2012, 6, 709–713. [Google Scholar] [CrossRef]
- Kashyap, R.; Chakraborty, S.; Zeng, S.; Swarnakar, S.; Kaur, S.; Doley, R.; Mondal, B. Enhanced Biosensing Activity of Bimetallic Surface Plasmon Resonance Sensor. Photonics 2019, 6, 108. [Google Scholar] [CrossRef] [Green Version]
- Elhani, S.; Ishitobi, H.; Inouye, Y.; Ono, A.; Hayashi, S.; Sekkat, Z. Surface Enhanced Visible Absorption of Dye Molecules in the Near-Field of Gold Nanoparticles. Sci. Rep. 2020, 10, 3913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeong, N.C.; Prasittichai, C.; Hupp, J.T. Photocurrent Enhancement by Surface Plasmon Resonance of Silver Nanoparticles in Highly Porous Dye-Sensitized Solar Cells. Langmuir 2011, 27, 14609–14614. [Google Scholar] [CrossRef]
- Zhou, X.; Liu, G.; Yu, J.; Fan, W. Surface plasmon resonance-mediated photocatalysis by noble metal-based composites under visible light. J. Mater. Chem. 2012, 22, 21337. [Google Scholar] [CrossRef]
- Knoll, W. Interfaces and thin films as seen by bound electromagnetic waves. Annu. Rev. Phys. Chem. 1998, 49, 569–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: New York, NY, USA, 2007. [Google Scholar]
- Brongersma, M.L.; Shalaev, V.M. The Case for Plasmonics. Science 2010, 328, 440–441. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S. Near-Field Optics and Surface Plasmon Polaritons; Springer: Berlin, Germany; New York, NY, USA, 2001. [Google Scholar]
- Kawata, S.; Inouye, Y.; Verma, P. Plasmonics for near-field nano-imaging and superlensing. Nat. Photon. 2009, 3, 388–394. [Google Scholar] [CrossRef]
- Stockman, M.I. Nanoplasmonics: Past, present, and glimpse into future. Opt. Express 2011, 19, 22029. [Google Scholar] [CrossRef] [Green Version]
- Rehman, S.; Rahmouni, A.; Mahfoud, T.; Nesterenko, D.V.; Sekkat, Z. Determination of the Optical Thickness of sub 10-nm Thin Metal Films by SPR Experiments. Plasmonics 2014, 9, 381–387. [Google Scholar] [CrossRef]
- Liu, C.; Liu, Q.; Hu, X. SPR phase detection for measuring the thickness of thin metal films. Opt. Express 2014, 22, 7574–7580. [Google Scholar] [CrossRef]
- Gonzalez-vila, A.; Debliquy, M.; Lahem, D.; Zhang, C.; Mégret, P.; Caucheteur, C. Molecularly imprinted electropolymerization on a metal-coated optical fiber for gas sensing applications. Sens. Actuators B Chem. 2017, 244, 1145–1151. [Google Scholar] [CrossRef]
- Refki, S.; Hayashi, S.; Rahmouni, A.; Nesterenko, D.V.; Sekkat, Z. Anticrossing Behavior of Surface Plasmon Polariton Dispersions in Metal-Insulator-Metal Structures. Plasmonics 2016, 11, 433–440. [Google Scholar] [CrossRef]
- Refki, S.; Hayashi, S.; Nesterenko, D.V.; Sekkat, Z.; Inoue, Y.; Kawata, S. Metal-insulator-metal structures for high-resolution sensing. In JSAP-OSA Joint Symposia 2014 Abstracts; Hokkaido: Sapporo, Japan, 2014; p. 19p_C3_5. [Google Scholar] [CrossRef]
- Sekkat, Z.; Hayashi, S.; Nesterenko, D.V.; Rahmouni, A.; Refki, S.; Ishitobi, H.; Inouye, Y.; Kawata, S. Plasmonic coupled modes in metal-dielectric multilayer structures: Fano resonance and giant field enhancement. Opt. Express 2016, 24, 20080. [Google Scholar] [CrossRef] [PubMed]
- Hayashi, S.; Nesterenko, D.V.; Rahmouni, A.; Sekkat, Z. Observation of Fano line shapes arising from coupling between surface plasmon polariton and waveguide modes. Appl. Phys. Lett. 2016, 108, 051101. [Google Scholar] [CrossRef] [Green Version]
- Hayashi, S.; Nesterenko, D.V.; Rahmouni, A.; Ishitobi, H.; Inouye, Y.; Kawata, S.; Sekkat, Z. Light-tunable Fano resonance in metal-dielectric multilayer structures. Sci. Rep. 2016, 6, 33144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parthenopoulos, D.A.; Rentzepis, P.M. Three-Dimensional Optical Storage Memory. Science 1989, 245, 843–845. [Google Scholar] [CrossRef] [PubMed]
- Maeda, M.; Ishitobi, H.; Sekkat, Z.; Kawata, S. Polarization storage by nonlinear orientational hole burning in azo dye-containing polymer films. Appl. Phys. Lett. 2004, 85, 351–353. [Google Scholar] [CrossRef]
- Sekkat, Z.; Dumont, M. Photoassisted poling of azo dye doped polymeric films at room temperature. Appl. Phys. B 1992, 54, 486–489. [Google Scholar] [CrossRef]
- Sekkat, Z.; Dumont, M. Poling of polymer films by photoisomerisation of azodye chromophores. Mol. Chryst. Liq. Chryst. Sci. Technol. B Nonlinear Opt. 1992, 2, 359–362. [Google Scholar]
- Xu, H.J.; Liu, F.; Elder, D.L.; Johnson, L.E.; De Coene, Y.; Clays, K.; Robinson, B.H.; Dalton, L.R. Ultrahigh electro-optic coefficients, High index of refraction, and long term stability from Diels-Alder Cross-Linkable Molecular Glasses. Chem. Mater. 2020, 32, 1408–1421. [Google Scholar] [CrossRef]
- Kalinin, A.A.; Islamova, L.N.; Shmelev, A.G.; Fazleeva, G.M.; Fominykh, O.D.; Dudkina, Y.B.; Vakhonina, T.A.; Levitskaya, A.I.; Sharipova, A.V.; Mukhtarov, A.S.; et al. D-pi-A chromophores with a quinoxaline core in the pi-bridge and bulky aryl groups in the acceptor: Synthesis, properties, and femtosecond nonlinear optical activity of the chromophore/PMMA guest-host materials. Dye. Pigment. 2021, 184, 108801. [Google Scholar] [CrossRef]
- Kuzyk, M.G.; Dawson, N.J. Photomechanical materials and applications: A tutorial. Adv. Opt. Photon. 2020, 12, 847. [Google Scholar] [CrossRef]
- Zhou, B.; Bernhardt, E.; Bhuyan, A.; Ghorbanishiadeh, Z.; Rasmussen, N.; Lanska, J.; Kuzyk, M.G. Theoretical and experimental studies of photomechanical materials [Invited]. J. Opt. Soc. Am. B 2019, 36, 1492. [Google Scholar] [CrossRef] [Green Version]
- Sekkat, Z. Optical tweezing by photomigration. Appl. Opt. 2016, 55, 259. [Google Scholar] [CrossRef] [PubMed]
- Sekkat, Z. Vectorial motion of matter induced by light fueled molecular machines. OSA Contin. 2018, 1, 668. [Google Scholar] [CrossRef]
- Moujdi, S.; Rahmouni, A.; Mahfoud, T.; Nesterenko, D.V.; Halim, M.; Sekkat, Z. Surface relief gratings in azo-polymers revisited. J. Appl. Phys. 2018, 124, 213103. [Google Scholar] [CrossRef]
- Sekkat, Z. Model for athermal enhancement of molecular mobility in solid polymers by light. Phys. Rev. E 2020, 102, 032501. [Google Scholar] [CrossRef] [PubMed]
- Ishitobi, H.; Akiyama, T.; Sekkat, Z.; Inouye, Y. Optical Trapping of Photosoftened Solid Polymers. J. Phys. Chem. C 2020, 124, 26037–26042. [Google Scholar] [CrossRef]
- Atkins, S.; Chueh, A.; Barwell, T.; Nunzi, J.-M.; Seroude, L. Capture and light-induced release of antibiotics by an azo dye polymer. Sci. Rep. 2020, 10, 3267. [Google Scholar] [CrossRef] [PubMed]
- Carmen, R.; Ursu, C.; Dascalu, M.; Asandulesa, M.; Tiron, V.; Bele, A.; Tugui, C.; Teodoroff-Onesim, S. Multi-stimuli responsive free-standing films of DR1- grafted silicones. Chem. Eng. J. 2020, 401, 126087. [Google Scholar] [CrossRef]
- Prêtre, P.; Wu, L.-M.; Knoesen, A.; Swalen, J.D. Optical properties of nonlinear optical polymers: A method for calculation. J. Opt. Soc. Am. B 1998, 15, 359. [Google Scholar] [CrossRef]
- Bondarenko, S.; Villringer, C.; Steglich, P. Comparative Study of Nano-Slot Silicon Waveguides Covered by Dye Doped and Undoped Polymer Cladding. Appl. Sci. 2018, 9, 89. [Google Scholar] [CrossRef] [Green Version]
- Taqatqa, O.; Al Attar, H. Spectroscopic ellipsometry investigation of azo dye and azo dye doped polymer. Eur. Phys. J. Appl. Phys. 2007, 37, 61–64. [Google Scholar] [CrossRef]
- Steglich, P.; Villringer, C.; Dietzel, B.; Mai, C.; Schrader, S.; Casalboni, M.; Mai, A. On-Chip Dispersion Measurement of the Quadratic Electro-Optic Effect in Nonlinear Optical Polymers Using a Photonic Integrated Circuit Technology. IEEE Photonics J. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Niklasson, G.A.; Granqvist, C.G.; Hunderi, O. Effective medium models for the optical properties of inhomogeneous materials. Appl. Opt. 1981, 20, 26–30. [Google Scholar] [CrossRef]
- Boyd, R.W.; Gehr, R.J.; Fischer, G.L.; Sipe, J.E. Nonlinear optical properties of nanocomposite materials. Pure Appl. Opt. 1996, 5, 505–512. [Google Scholar] [CrossRef]
- Lee, K.J.; Kang, T.D.; Lee, H.S.; Lee, H.K. Ellipsometric study of polymer thin films: Nonlinear optical guest-host system. J. Appl. Phys. 2005, 97, 083543. [Google Scholar] [CrossRef]
- Sekkat, Z.; Knoll, W. (Eds.) Photoreactive Organic Thin Films; Academic Press: Amsterdam, The Netherlands; Boston, MA, USA, 2002. [Google Scholar]
- Sekkat, Z.; Prêtre, P.; Knoesen, A.; Volksen, W.; Lee, V.Y.; Miller, R.D.; Wood, J.; Knoll, W. Correlation between polymer architecture and sub-glass-transition-temperature light-induced molecular movement in azo-polyimide polymers: Influence on linear and second- and third-order nonlinear optical processes. J. Opt. Soc. Am. B 1998, 15, 401. [Google Scholar] [CrossRef]
- Zeroni, I.; Lodge, T.P. Chain Dimensions in Poly(ethylene oxide)/ Poly(methyl methacrylate) Blends. Macromolecules 2008, 41, 1050–1052. [Google Scholar] [CrossRef]
- Swalen, J.D.; Bjorklund, G.C.; Fleming, W.W.; Hung, R.Y.; Jurich, M.C.; Lee, V.Y.; Miller, R.D.; Moerner, W.E.; Morichere, D.Y.; Skumanich, A.; et al. NLO Polymeric Waveguide Electro-Optic Phase Modulator. Proc. SPIE Int. Soc. Opt. Eng. 1993, 1775. [Google Scholar] [CrossRef]
- Kuzyk, M.G.; Sohn, J.E.; Dirk, C.W. Mechanisms of quadratic electro-optic modulation of dye-doped polymer systems. J. Opt. Soc. Am. B 1990, 7, 842–858. [Google Scholar] [CrossRef]
- Kretschmann, E. Decay of non radiative surface plasmons into light on rough silver films. Comparison of experimental and theoretical results. Opt. Commun. 1972, 6, 185–187. [Google Scholar] [CrossRef]
- Aust, E.F.; Sawodny, M.; Ito, S.; Knoll, W. Surface plasmon and guided optical wave microscopies. Scanning 1994, 16, 353–362. [Google Scholar] [CrossRef]
- Borstel, G.; Falge, H.J. Surface polaritons in semi-infinite crystals. Appl. Phys. 1978, 16, 211–223. [Google Scholar] [CrossRef]
- Polyanskiy, M. Refractive Index. 2014. Available online: https://refractiveindex.info/?shelf=glass&book=BK7&page=SCHOTT (accessed on 19 January 2021).
- Refki, S.; Hayashi, S.; Ishitobi, H.; Nesterenko, D.V.; Rahmouni, A.; Inouye, Y.; Sekkat, Z. Resolution Enhancement of Plasmonic Sensors by Metal-Insulator-Metal Structures. Ann. Phys. 2018, 530, 1700411. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Elhani, S.; Maouli, I.; Refki, S.; Halim, M.; Hayashi, S.; Sekkat, Z. Quantitative analyses of optically induced birefringence in azo dye containing polymers. J. Opt. 2019, 21, 115401. [Google Scholar] [CrossRef]
- Jellison, G.E. Data analysis for spectroscopic ellipsometry. Thin Solid Film. 1993, 234, 416–422. [Google Scholar] [CrossRef]
- Woollam, J.A. VASE Manual; Woollam, J.A. Inc.: Lincoln, NE, USA, 1997. [Google Scholar]
- Bruggeman, D.A.G. Berechnung verschiedener physikalischer Konstanten von heterogenen Substanzen. I. Dielektrizitätskonstanten und Leitfähigkeiten der Mischkörper aus isotropen Substanzen. Ann. Phys. 1935, 416, 636–664. [Google Scholar] [CrossRef]





| DR1/PMMA Concentration | Literature | SPR a | Ellipsometry a | UV-Vis a | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 632.8 nm | 632.8 nm | 488 nm | 632.8 nm | 488 nm | 632.8 nm | |||||
| n | κ | n | κ | n | κ | n | κ | κ | κ | |
| Neat DR1 | 2.0536 b | - | - | - | 1.835 | 1.058 | 2.136 | 0.126 | - | - |
| 8% w/w | - | - | 1.5401 | 0.0075 | 1.534 | 0.082 | 1.537 | 0.008 | 0.0925 | 0.0065 |
| 10% w/w | 1.5450 c | 0.008 c | 1.5540 | 0.0101 | 1.545 | 0.098 | 1.550 | 0.011 | 0.1094 | 0.0108 |
| 12% w/w | - | - | 1.5650 | 0.0120 | 1.553 | 0.120 | 1.561 | 0.012 | 0.1279 | 0.0115 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andam, N.; Refki, S.; Ishitobi, H.; Inouye, Y.; Sekkat, Z. Optical Characterization of Ultra-Thin Films of Azo-Dye-Doped Polymers Using Ellipsometry and Surface Plasmon Resonance Spectroscopy. Photonics 2021, 8, 41. https://doi.org/10.3390/photonics8020041
Andam N, Refki S, Ishitobi H, Inouye Y, Sekkat Z. Optical Characterization of Ultra-Thin Films of Azo-Dye-Doped Polymers Using Ellipsometry and Surface Plasmon Resonance Spectroscopy. Photonics. 2021; 8(2):41. https://doi.org/10.3390/photonics8020041
Chicago/Turabian StyleAndam, Najat, Siham Refki, Hidekazu Ishitobi, Yasushi Inouye, and Zouheir Sekkat. 2021. "Optical Characterization of Ultra-Thin Films of Azo-Dye-Doped Polymers Using Ellipsometry and Surface Plasmon Resonance Spectroscopy" Photonics 8, no. 2: 41. https://doi.org/10.3390/photonics8020041
APA StyleAndam, N., Refki, S., Ishitobi, H., Inouye, Y., & Sekkat, Z. (2021). Optical Characterization of Ultra-Thin Films of Azo-Dye-Doped Polymers Using Ellipsometry and Surface Plasmon Resonance Spectroscopy. Photonics, 8(2), 41. https://doi.org/10.3390/photonics8020041