An Inexpensive Portable Self-Reference Module for Digital Holographic Microscopy
Abstract
:1. Introduction
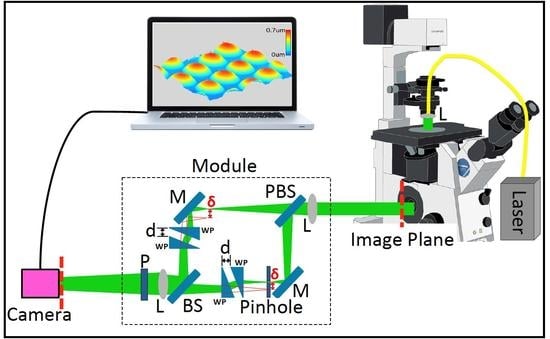
2. The Nearly Common-Path Module
2.1. Design Considerations
2.2. Experimental System
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Mir, M.; Bhaduri, B.; Wang, R.; Zhu, R.; Popescu, G. Quantitative phase imaging. Prog. Opt. 2012, 57, 133–217. [Google Scholar]
- Lee, K.; Kim, K.; Jung, J.; Heo, J.; Cho, S.; Lee, S.; Chang, G.; Jo, Y.; Park, H.; Park, Y. Quantitative phase imaging techniques for the study of cell pathophysiology: From principles to applications. Sensors 2013, 13, 4170–4191. [Google Scholar] [CrossRef]
- Kemper, B.; von Bally, G. Digital holographic microscopy for live cell applications and technical inspection. Appl. Opt. 2008, 47, A52–A61. [Google Scholar] [CrossRef]
- Marquet, P.; Rappaz, B.; Magistretti, P.J.; Cuche, E.; Emery, Y.; Colomb, T.; Depeursinge, C. Digital holographic microscopy: A noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy. Opt. Lett. 2005, 30, 468–470. [Google Scholar] [CrossRef] [Green Version]
- Zhou, R.; Edwards, C.; Arbabi, A.; Popescu, G.; Goddard, L.L. Detecting 20 nm wide defects in large area nanopatterns using optical interferometric microscopy. Nano Lett. 2013, 13, 3716–3721. [Google Scholar] [CrossRef] [PubMed]
- Khadir, S.; Bon, P.; Vignaud, D.; Galopin, E.; McEvoy, N.; McCloskey, D.; Monneret, S.; Baffou, G. Optical imaging and characterization of graphene and other 2D materials using quantitative phase microscopy. ACS Photonics 2017, 4, 3130–3139. [Google Scholar] [CrossRef]
- Cuche, E.; Marquet, P.; Depeursinge, C. Simultaneous amplitude-contrast and quantitative phase-contrast microscopy by numerical reconstruction of Fresnel off-axis holograms. Appl. Opt. 1999, 38, 6994–7001. [Google Scholar] [CrossRef] [PubMed]
- Mann, C.J.; Yu, L.; Lo, C.M.; Kim, M.K. High-resolution quantitative phase-contrast microscopy by digital holography. Opt. Express 2005, 13, 8693–8698. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Millet, L.; Mir, M.; Ding, H.; Unarunotai, S.; Rogers, J.; Gillette, M.U.; Popescu, G. Spatial light interference microscopy (SLIM). Opt. Express 2011, 19, 1016–1026. [Google Scholar] [CrossRef] [PubMed]
- Bhaduri, B.; Pham, H.; Mir, M.; Popescu, G. Diffraction phase microscopy with white light. Opt. Lett. 2012, 37, 1094–1096. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tian, L.; Wang, J.; Waller, L. 3D differential phase-contrast microscopy with computational illumination using an LED array. Opt. Lett. 2014, 39, 1326–1329. [Google Scholar] [CrossRef] [Green Version]
- Phillips, Z.F.; Chen, M.; Waller, L. Single-shot quantitative phase microscopy with color-multiplexed differential phase contrast (cDPC). PLoS ONE 2017, 12, e0171228. [Google Scholar] [CrossRef] [Green Version]
- Zuo, C.; Sun, J.; Li, J.; Zhang, J.; Asundi, A.; Chen, Q. High-resolution transport-of-intensity quantitative phase microscopy with annular illumination. Sci. Rep. 2017, 7, 7654. [Google Scholar] [CrossRef]
- Zuo, C.; Chen, Q.; Qu, W.; Asundi, A. High-speed transport-of-intensity phase microscopy with an electrically tunable lens. Opt. Express 2013, 21, 24060–24075. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; Zhang, Y.; Göröcs, Z.; Feizi, A.; Ozcan, A. Propagation phasor approach for holographic image reconstruction. Sci. Rep. 2016, 6, 22738. [Google Scholar] [CrossRef]
- Rivenson, Y.; Zhang, Y.; Günaydın, H.; Teng, D.; Ozcan, A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light. Sci. Appl. 2018, 7, 17141. [Google Scholar] [CrossRef]
- Gabai, H.; Shaked, N.T. Dual-channel low-coherence interferometry and its application to quantitative phase imaging of fingerprints. Opt. Express 2012, 20, 26906–26912. [Google Scholar] [CrossRef]
- Mirsky, S.K.; Barnea, I.; Levi, M.; Greenspan, H.; Shaked, N.T. Automated analysis of individual sperm cells using stain-free interferometric phase microscopy and machine learning. Cytometry Part A 2017, 91, 893–900. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roitshtain, D.; Wolbromsky, L.; Bal, E.; Greenspan, H.; Satterwhite, L.L.; Shaked, N.T. Quantitative phase microscopy spatial signatures of cancer cells. Cytometry Part A 2017, 91, 482–493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Colomb, T.; Cuche, E.; Charrière, F.; Kühn, J.; Aspert, N.; Montfort, F.; Marquet, P.; Depeursinge, C. Automatic procedure for aberration compensation in digital holographic microscopy and applications to specimen shape compensation. Appl. Opt. 2006, 45, 851–863. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Colomb, T.; Kühn, J.; Charrière, F.; Depeursinge, C.; Marquet, P.; Aspert, N. Total aberrations compensation in digital holographic microscopy with a reference conjugated hologram. Opt. Express 2006, 14, 4300–4306. [Google Scholar] [CrossRef] [PubMed]
- Molony, K.M.; Hennelly, B.M.; Kelly, D.P.; Naughton, T.J. Reconstruction algorithms applied to in-line Gabor digital holographic microscopy. Opt. Commun. 2010, 283, 903–909. [Google Scholar] [CrossRef] [Green Version]
- Kelly, D.; Hennelly, B.M.; McElhinney, C.; Naughton, T.J. A Practical Guide to Digital Holography and Generalized Sampling. In Optics and Photonics for Information Processing II; International Society for Optics and Photonics: Bellingham, WA, USA, 2008; Volume 7072, p. 707215. [Google Scholar]
- Langehanenberg, P.; Kemper, B.; Dirksen, D.; Von Bally, G. Autofocusing in digital holographic phase contrast microscopy on pure phase objects for live cell imaging. Appl. Opt. 2008, 47, D176–D182. [Google Scholar] [CrossRef]
- Fan, X.; Healy, J.J.; Hennelly, B.M. Investigation of sparsity metrics for autofocusing in digital holographic microscopy. Opt. Eng. 2017, 56, 053112. [Google Scholar] [CrossRef]
- Popescu, G.; Ikeda, T.; Dasari, R.R.; Feld, M.S. Diffraction phase microscopy for quantifying cell structure and dynamics. Opt. Lett. 2006, 31, 775–777. [Google Scholar] [CrossRef]
- Ding, H.; Popescu, G. Instantaneous spatial light interference microscopy. Opt. Express 2010, 18, 1569–1575. [Google Scholar] [CrossRef]
- Mico, V.; Zalevsky, Z.; García, J. Common-path phase-shifting digital holographic microscopy: A way to quantitative phase imaging and superresolution. Opt. Commun. 2008, 281, 4273–4281. [Google Scholar] [CrossRef]
- Jang, J.; Bae, C.Y.; Park, J.K.; Ye, J.C. Self-reference quantitative phase microscopy for microfluidic devices. Opt. Lett. 2010, 35, 514–516. [Google Scholar] [CrossRef] [Green Version]
- Kemper, B.; Vollmer, A.; von Bally, G.; Rommel, C.E.; Schnekenburger, J. Simplified approach for quantitative digital holographic phase contrast imaging of living cells. J. Biomed. Opt. 2011, 16, 026014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shaked, N.T.; Zhu, Y.; Badie, N.; Bursac, N.; Wax, A.P. Reflective interferometric chamber for quantitative phase imaging of biological sample dynamics. J. Biomed. Opt. 2010, 15, 030503. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shaked, N.T. Quantitative phase microscopy of biological samples using a portable interferometer. Opt. Lett. 2012, 37, 2016–2018. [Google Scholar] [CrossRef]
- Girshovitz, P.; Shaked, N.T. Compact and portable low-coherence interferometer with off-axis geometry for quantitative phase microscopy and nanoscopy. Opt. Express 2013, 21, 5701–5714. [Google Scholar] [CrossRef] [Green Version]
- Nativ, A.; Shaked, N.T. Compact interferometric module for full-field interferometric phase microscopy with low spatial coherence illumination. Opt. Lett. 2017, 42, 1492–1495. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bon, P.; Maucort, G.; Wattellier, B.; Monneret, S. Quadriwave lateral shearing interferometry for quantitative phase microscopy of living cells. Opt. Express 2009, 17, 13080–13094. [Google Scholar] [CrossRef] [PubMed]
- Burmak, L. Digital Holographic Imaging Based on Mach-Zehnder near Common-Path Interferometer. In Unconventional Optical Imaging II; International Society for Optics and Photonics: Bellingham, WA, USA, 2020; Volume 11351, p. 113511K. [Google Scholar]
- Goodman, J.W. Introduction to Fourier Optics; Roberts & Company Publishers: Greenwood Village, CO, USA, 2004. [Google Scholar]
- Hennelly, B.M.; Sheridan, J.T. Generalizing, optimizing, and inventing numerical algorithms for the fractional Fourier, Fresnel, and linear canonical transforms. JOSA A 2005, 22, 917–927. [Google Scholar] [CrossRef] [Green Version]
- Ahrenberg, L.; Page, A.J.; Hennelly, B.M.; McDonald, J.B.; Naughton, T.J. Using commodity graphics hardware for real-time digital hologram view-reconstruction. J. Disp. Technol. 2009, 5, 111–119. [Google Scholar] [CrossRef] [Green Version]
- Herráez, M.A.; Burton, D.R.; Lalor, M.J.; Gdeisat, M.A. Fast two-dimensional phase-unwrapping algorithm based on sorting by reliability following a noncontinuous path. Appl. Opt. 2002, 41, 7437–7444. [Google Scholar] [CrossRef]
- Edwards, C.; Bhaduri, B.; Nguyen, T.; Griffin, B.G.; Pham, H.; Kim, T.; Popescu, G.; Goddard, L.L. Effects of spatial coherence in diffraction phase microscopy. Opt. Express 2014, 22, 5133–5146. [Google Scholar] [CrossRef] [PubMed] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, X.; Tang, Z.; O’Dwyer, K.; Hennelly, B.M. An Inexpensive Portable Self-Reference Module for Digital Holographic Microscopy. Photonics 2021, 8, 277. https://doi.org/10.3390/photonics8070277
Fan X, Tang Z, O’Dwyer K, Hennelly BM. An Inexpensive Portable Self-Reference Module for Digital Holographic Microscopy. Photonics. 2021; 8(7):277. https://doi.org/10.3390/photonics8070277
Chicago/Turabian StyleFan, Xin, Zhengyuan Tang, Kevin O’Dwyer, and Bryan M. Hennelly. 2021. "An Inexpensive Portable Self-Reference Module for Digital Holographic Microscopy" Photonics 8, no. 7: 277. https://doi.org/10.3390/photonics8070277
APA StyleFan, X., Tang, Z., O’Dwyer, K., & Hennelly, B. M. (2021). An Inexpensive Portable Self-Reference Module for Digital Holographic Microscopy. Photonics, 8(7), 277. https://doi.org/10.3390/photonics8070277