Sorption Isotherms and Thermodynamic Properties of Pomegranate Peels
Abstract
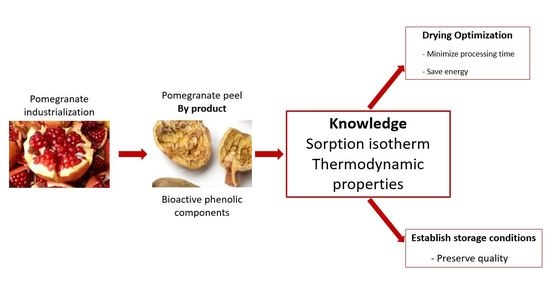
:1. Introduction
2. Materials and Methods
2.1. Raw Material
2.2. Experimental Determination of Sorption Isotherms
2.3. Modeling
2.4. Determination of Isosteric Heat
2.5. Differential Sorption Enthalpy and Sorption Entropy
2.6. Enthalpy–Entropy Compensation Theory
3. Results and Discussion
3.1. Experimental Moisture Sorption Isotherms
3.2. Modeling of the Sorption Isotherms of the Pomegranate Peels
3.3. Isosteric Heat of Sorption
3.4. Thermodynamic Properties
3.5. Enthalpy–Entropy Compensation Theory
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- El Barnossi, A.; Moussaid, F.; Iraqi Housseini, A. Tangerine, Banana and Pomegranate Peels Valorisation for Sustainable Environment: A Review. Biotechnol. Rep. 2021, 29, e00574. [Google Scholar] [CrossRef] [PubMed]
- Boussaa, F.; Zaouay, F.; Burlo-Carbonell, F.; Nuncio-Jáuregui, N.; Gmati, M.; El Arbi, B.; Melgarejo, P.; Hernandez, F.; Mars, M. Combined Effects of Cropping System and Harvest Date Determine Quality and Nutritional Value of Pomegranate Fruits (Punica granatum L. cv. Gabsi). Sci. Hortic. 2019, 249, 419–431. [Google Scholar] [CrossRef]
- Saadi, W.; Rodríguez-Sánchez, S.; Ruiz, B.; Najar-Souissi, S.; Ouederni, A.; Fuente, E. From Pomegranate Peels Waste to One-Step Alkaline Carbonate Activated Carbons. Prospect as Sustainable Adsorbent for the Renewable Energy Production. J. Environ. Chem. Eng. 2022, 10, 107010. [Google Scholar] [CrossRef]
- Silva, L.D.O.; Garrett, R.; Monteiro, M.L.G.; Conte-Junior, C.A.; Torres, A.G. Pomegranate (Punica granatum) Peel Fractions Obtained by Supercritical CO2 Increase Oxidative and Colour Stability of Bluefish (Pomatomus saltatrix) Patties Treated by UV-C Irradiation. Food Chem. 2021, 362, 130159. [Google Scholar] [CrossRef]
- Andrade, M.A.; Lima, V.; Sanches Silva, A.; Vilarinho, F.; Castilho, M.C.; Khwaldia, K.; Ramos, F. Pomegranate and Grape By-Products and Their Active Compounds: Are They a Valuable Source for Food Applications? Trends Food Sci. Technol. 2019, 86, 68–84. [Google Scholar] [CrossRef]
- Amir, R.; Borochov-Neori, H.; Tian, L.; Holland, D. The Biodiversity of Different Traits of Pomegranate Fruit Peels from a Broad Collection of Diverse Cultivars. Sci. Hortic. 2019, 246, 842–848. [Google Scholar] [CrossRef]
- Khwairakpam, A.D.; Bordoloi, D.; Thakur, K.K.; Monisha, J.; Arfuso, F.; Sethi, G.; Mishra, S.; Kumar, A.P.; Kunnumakkara, A.B. Possible Use of Punica granatum (Pomegranate) in Cancer Therapy. Pharmacol. Res. 2018, 133, 53–64. [Google Scholar] [CrossRef] [Green Version]
- Singh, B.; Singh, J.P.; Kaur, A.; Singh, N. Phenolic Compounds as Beneficial Phytochemicals in Pomegranate (Punica granatum L.) Peel: A Review. Food Chem. 2018, 261, 75–86. [Google Scholar] [CrossRef]
- El-Mesery, H.S. Improving the Thermal Efficiency and Energy Consumption of Convective Dryer Using Various Energy Sources for Tomato Drying. Alex. Eng. J. 2022, 61, 10245–10261. [Google Scholar] [CrossRef]
- Li, H.; Xie, L.; Ma, Y.; Zhang, M.; Zhao, Y.; Zhao, X. Effects of Drying Methods on Drying Characteristics, Physicochemical Properties and Antioxidant Capacity of Okra. LWT Food Sci. Technol. 2019, 101, 630–638. [Google Scholar] [CrossRef]
- Cuevas, M.; Martínez-Cartas, M.L.; Pérez-Villarejo, L.; Hernández, L.; García-Martín, J.F.; Sánchez, S. Drying Kinetics and Effective Water Diffusivities in Olive Stone and Olive-Tree Pruning. Renew. Energy 2019, 132, 911–920. [Google Scholar] [CrossRef]
- Amadou, H.; Leonard, A.; Bouchekima, B. Determination of Desorption Isotherms Using the DVS Apparatus (Dynamic Vapor Sorption System) at Different Temperatures on Unblanched and Blanched Samples of Potato. J. App. Sci. Res. 2015, 3, 8–12. [Google Scholar]
- Thybring, E.E.; Boardman, C.R.; Zelinka, S.L.; Glass, S.V. Common Sorption Isotherm Models Are Not Physically Valid for Water in Wood. Colloids Surfaces A Physicochem. Eng. Asp. 2021, 627, 127214. [Google Scholar] [CrossRef]
- Arslan-Tontul, S. Moisture Sorption Isotherm, Isosteric Heat and Adsorption Surface Area of Whole Chia Seeds. LWT Food Sci. Technol. 2020, 119, 108859. [Google Scholar] [CrossRef]
- Getahun, E.; Gabbiye, N.; Delele, M.A.; Fanta, S.W.; Gebrehiwot, M.G.; Vanierschot, M. Effect of Maturity on the Moisture Sorption Isotherm of Chili Pepper (Mareko Fana Variety). Heliyon 2020, 6, e04608. [Google Scholar] [CrossRef]
- Paes, M.S.; de AlcântaraPessoa Filho, P.; Tadini, C.C. Sorption Properties of Cambuci (Campomanesia phaea O. Berg) Untreated and Pre-Treated with Sorbitol as Osmotic Solute. LWT Food Sci. Technol. 2021, 139, 110569. [Google Scholar] [CrossRef]
- Al-Ghamdi, S.; Hong, Y.K.; Qu, Z.; Sablani, S.S. State Diagram, Water Sorption Isotherms and Color Stability of Pumpkin (Cucurbita pepo L.). J. Food Eng. 2020, 273, 109820. [Google Scholar] [CrossRef]
- Bui, R.; Labat, M.; Aubert, J.-E. Comparison of the Saturated Salt Solution and the Dynamic Vapor Sorption Techniques Based on the Measured Sorption Isotherm of Barley Straw. Constr. Build. Mater. 2017, 141, 140–151. [Google Scholar] [CrossRef]
- Demarchi, S.M.; Quintero Ruiz, N.A.; De Michelis, A.; Giner, S.A. Sorption Characteristics of Rosehip, Apple and Tomato Pulp Formulations as Determined by Gravimetric and Hygrometric Methods. LWT Food Sci. Technol. 2013, 52, 21–26. [Google Scholar] [CrossRef]
- Goneli, A.L.D.; Corrêa, P.C.; Oliveira, G.H.H.; Afonso Júnior, P.C. Water Sorption Properties of Coffee Fruits, Pulped and Green Coffee. LWT Food Sci. Technol. 2013, 50, 386–391. [Google Scholar] [CrossRef]
- Sánchez-Torres, E.A.; Abril, B.; Benedito, J.; Bon, J.; García-Pérez, J.V. Water Desorption Isotherms of Pork Liver and Thermodynamic Properties. LWT Food Sci. Technol. 2021, 149, 111857. [Google Scholar] [CrossRef]
- Borsini, A.A.; Llavata, B.; Umaña, M.; Cárcel, J.A. Artichoke by Products as a Source of Antioxidant and Fiber: How It Can Be Affected by Drying Temperature. Foods 2021, 10, 459. [Google Scholar] [CrossRef]
- AOAC International. Official Methods of Analysis; AOAC: Rockville, ML, USA, 1980; Volume 552, ISBN 0935584145. [Google Scholar]
- García-Pérez, J.V.; Cárcel, J.A.; Clemente, G.; Mulet, A. Water Sorption Isotherms for Lemon Peel at Different Temperatures and Isosteric Heats. LWT Food Sci. Technol. 2008, 41, 18–25. [Google Scholar] [CrossRef]
- Andrade, R.D.; Lemus, R.; Pérez, C.E. Models of Sorption Isotherms for Food: Uses and Limitations. Modelos De Isotermas De Sorcion Para Alimentos: Usos Y Limitaciones. Vitae 2011, 18, 325–334. [Google Scholar]
- Khawaja, M.; Mubarak, S.; Zia-Ur-rehman, M.; Kazi, A.A.; Hamid, A. Adsorption Studies of Pomegranate Peel Activated Charcoal for Nickel (II) Ion. J. Chil. Chem. Soc. 2015, 60, 2642–2645. [Google Scholar] [CrossRef] [Green Version]
- Camaño Echavarria, J.A.; Rivera Torres, A.M.; Zapata Montoya, J.E. Sorption Isotherms and Thermodynamic Properties of the Dry Silage of Red Tilapia Viscera (Oreochromis spp.) Obtained in a Direct Solar Dryer. Heliyon 2021, 7, e06798. [Google Scholar] [CrossRef] [PubMed]
- Bougayr, E.H.; Lakhal, E.K.; Idlimam, A.; Lamharrar, A.; Kouhila, M.; Berroug, F. Experimental Study of Hygroscopic Equilibrium and Thermodynamic Properties of Sewage Sludge. Appl. Therm. Eng. 2018, 143, 521–531. [Google Scholar] [CrossRef]
- Toǧrul, H.; Arslan, N. Moisture Sorption Behaviour and Thermodynamic Characteristics of Rice Stored in a Chamber under Controlled Humidity. Biosyst. Eng. 2006, 95, 181–195. [Google Scholar] [CrossRef]
- Rosa, D.P.; Evangelista, R.R.; Borges Machado, A.L.; Sanches, M.A.R.; Telis-Romero, J. Water Sorption Properties of Papaya Seeds (Carica papaya L.) Formosa Variety: An Assessment under Storage and Drying Conditions. LWT Food Sci. Technol. 2021, 138, 110458. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of Gases in Multimolecular Layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
- Kammoun Bejar, A.; Boudhrioua Mihoubi, N.; Kechaou, N. Moisture Sorption Isotherms—Experimental and Mathematical Investigations of Orange (Citrus sinensis) Peel and Leaves. Food Chem. 2012, 132, 1728–1735. [Google Scholar] [CrossRef]
- Hssaini, L.; Ouaabou, R.; Charafi, J.; Idlimam, A.; Lamharrar, A.; Razouk, R.; Hanine, H. Hygroscopic Proprieties of Fig (Ficus carica L.): Mathematical Modelling of Moisture Sorption Isotherms and Isosteric Heat Kinetics. S. Afr. J. Bot. 2020, 145, 265–274. [Google Scholar] [CrossRef]
- Blahovec, J. Sorption Isotherms in Materials of Biological Origin Mathematical and Physical Approach. J. Food Eng. 2004, 65, 489–495. [Google Scholar] [CrossRef]
- Moussaoui, H.; Bahammou, Y.; Idlimam, A.; Lamharrar, A.; Abdenouri, N. Investigation of Hygroscopic Equilibrium and Modeling Sorption Isotherms of the Argan Products: A Comparative Study of Leaves, Pulps, and Fruits. Food Bioprod. Processing 2019, 114, 12–22. [Google Scholar] [CrossRef]
- Quirijns, E.J.; Van Boxtel, A.J.B.; Van Loon, W.K.P.; Van Straten, G. Sorption Isotherms, GAB Parameters and Isosteric Heat of Sorption. J. Sci. Food Agric. 2005, 85, 1805–1814. [Google Scholar] [CrossRef]
- Ribeiro-Filho, N.; Akepach, P.; Sanchez de Alsina, O.L. Hygroscopicity and Isosteric Heat of Cashew Apple Waste, Non-Fermented and Fermented. Food Biosci. 2021, 42, 101103. [Google Scholar] [CrossRef]
- Vega-Gálvez, A.; López, J.; Ah-Hen, K.; Torres, M.J.; Lemus-Mondaca, R. Thermodynamic Properties, Sorption Isotherms and Glass Transition Temperature of Cape Gooseberry (Physalis peruviana L.). Food Technol. Biotechnol. 2014, 52, 83–92. [Google Scholar]





| Model | Equation | Parameters | Reference |
|---|---|---|---|
| GAB | Xm: moisture content of the monolayer C: Guggenheim constant linked to the sorption heat of the monolayer K: constant linked to the sorption heat of the multilayer | [24] | |
| BET | Xm: moisture content of the monolayer C: papameter linked to the heat released during the sorption process | [24] | |
| Freundlich | K, n: model parameters related to the product | [26] | |
| Henderson | f, n: model parameters related to the product | [27] | |
| Oswin | A, B: model parameters related to the product | [15] | |
| Peleg | A, B, C, D: model parameters related to the product | [28] | |
| Caurie | Xs: moisture content which provides stability during storage V: parameter linked with the product | [27] | |
| Smith | A, B: model parameters related to the product | [29] |
| Model Name | Model Parameters and Fitting Assess | 20 °C | 30 °C | 40 °C | 50 °C |
|---|---|---|---|---|---|
| GAB | Xm | 0.26 ± 0.05 | 0.23 ± 0.04 | 0.20 ± 0.03 | 0.18 ± 0.03 |
| C | 4.4 ± 0.8 | 6.0 ± 0.9 | 10 ± 1 | 12 ± 1 | |
| K | 0.9 ± 0.2 | 0.9 ± 0.1 | 1.0 ± 0.1 | 1.0 ± 0.1 | |
| SSE | 0.8120 | 0.6435 | 0.4523 | 0.5276 | |
| R2 | 0.9554 | 0.9647 | 0.9752 | 0.9710 | |
| RMSE | 0.1767 | 0.1573 | 0.1319 | 0.1424 | |
| BET | Xm | 0.32 ± 0.06 | 0.29 ± 0.05 | 0.25 ± 0.04 | 0.23 ± 0.04 |
| C | 0.9 ± 0.1 | 0.9 ± 0.1 | 0.9 ± 0.1 | 0.9 ± 0.1 | |
| SSE | 0.8530 | 0.7181 | 0.5959 | 0.6887 | |
| R2 | 0.9532 | 0.9606 | 0.9673 | 0.9622 | |
| RMSE | 0.1777 | 0.1631 | 0.1486 | 0.1597 | |
| Feundlich | K | 2.8 ± 0.6 | 2.9 ± 0.6 | 3.0 ± 0.6 | 3.0 ± 0.7 |
| N | 0.18 ± 0.04 | 0.16 ± 0.03 | 0.14 ± 0.03 | 0.13 ± 0.03 | |
| SSE | 1.2860 | 1.1990 | 1.1740 | 1.2920 | |
| R2 | 0.9294 | 0.9342 | 0.9355 | 0.9290 | |
| RMSE | 0.2182 | 0.2107 | 0.2085 | 0.2188 | |
| Henderson | f | −1.7 ± 0.4 | −1.5 ± 0.3 | −1.3 ± 0.2 | −1.2 ± 0.2 |
| n | 1.0 ± 0.2 | 0.9 ± 0.2 | 0.8 ± 0.1 | 0.7 ± 0.1 | |
| SSE | 1.3970 | 1.0860 | 0.7650 | 0.8480 | |
| R2 | 0.9233 | 0.9382 | 0.9580 | 0.9534 | |
| RMSE | 0.2274 | 0.2005 | 0.1683 | 0.1772 | |
| Oswin | A | 0.6 ± 0.2 | 0.5 ± 0.1 | 0.41 ± 0.08 | 0.39 ± 0.07 |
| B | 0.4 ± 0.1 | 0.4 ± 0.1 | 0.50 ± 0.09 | 0.5 ± 0.1 | |
| SSE | 2.6620 | 1.8976 | 0.9482 | 0.9266 | |
| R2 | 0.8538 | 0.8975 | 0.9479 | 0.9491 | |
| RMSE | 0.3140 | 0.2629 | 0.1874 | 0.1853 | |
| Peleg | A | 0.47 ± 0.05 | 0.48 ± 0.06 | 0.50 ± 0.05 | 0.51 ± 0.06 |
| B | 0.54 ± 0.05 | 0.55 ± 0.06 | 0.61 ± 0.06 | 0.63 ± 0.07 | |
| C | 2.6 ± 0.2 | 2.7 ± 0.3 | 2.8 ± 0.3 | 2.9 ± 0.3 | |
| D | 8.7 ± 0.8 | 10 ± 1 | 11 ± 1 | 12 ± 1 | |
| SSE | 0.4728 | 0.3348 | 0.2320 | 0.3174 | |
| R2 | 0.9740 | 0.9816 | 0.9873 | 0.9826 | |
| RMSE | 0.0971 | 0.1157 | 0.0963 | 0.1127 | |
| Caurie | V | 374 ± 73 | 648 ± 123 | 1352 ± 163 | 2398 ± 257 |
| Xs | 22 ± 4 | 24 ± 5 | 28 ± 5 | 30 ± 6 | |
| SSE | 1.039 | 0.9785 | 0.98 | 1.121 | |
| R2 | 0.943 | 0.9463 | 0.9462 | 0.9385 | |
| RMSE | 0.1961 | 0.1904 | 0.1905 | 0.2037 | |
| Smith | A | −0.6 ± 0.1 | −0.6 ± 0.1 | −0.6 ± 0.1 | −0.7 ± 0.1 |
| B | 0.006 ± 0.001 | −0.023 ± 0.005 | −0.05 ± 0.01 | −0.06 ± 0.01 | |
| SSE | 1.4020 | 1.1950 | 1.1400 | 1.3440 | |
| R2 | 0.9230 | 0.9344 | 0.9374 | 0.9262 | |
| RMSE | 0.2279 | 0.2104 | 0.2055 | 0.2231 |
| Xeq | qstn (J/mol) | Qst (J/mol) |
|---|---|---|
| 0.11 | 8423.9 | 51,923.9 |
| 0.12 | 7730.0 | 51,230.0 |
| 0.13 | 7332.8 | 50,832.8 |
| 0.14 | 6322.0 | 49,822.0 |
| 0.15 | 5484.2 | 48,984.2 |
| 0.16 | 5193.3 | 48,693.3 |
| 0.17 | 4898.3 | 48,398.3 |
| 0.18 | 4596.1 | 48,096.1 |
| 0.19 | 4116.6 | 47,616.6 |
| 0.2 | 3837.7 | 47,337.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Slimane, N.; Bagane, M.; Mulet, A.; Carcel, J.A. Sorption Isotherms and Thermodynamic Properties of Pomegranate Peels. Foods 2022, 11, 2009. https://doi.org/10.3390/foods11142009
Ben Slimane N, Bagane M, Mulet A, Carcel JA. Sorption Isotherms and Thermodynamic Properties of Pomegranate Peels. Foods. 2022; 11(14):2009. https://doi.org/10.3390/foods11142009
Chicago/Turabian StyleBen Slimane, Nihel, Mohamed Bagane, Antonio Mulet, and Juan A. Carcel. 2022. "Sorption Isotherms and Thermodynamic Properties of Pomegranate Peels" Foods 11, no. 14: 2009. https://doi.org/10.3390/foods11142009
APA StyleBen Slimane, N., Bagane, M., Mulet, A., & Carcel, J. A. (2022). Sorption Isotherms and Thermodynamic Properties of Pomegranate Peels. Foods, 11(14), 2009. https://doi.org/10.3390/foods11142009