Analysis of Postoperative Remodeling Characteristics after Modular Inner Branched Stent-Graft Treatment of Aortic Arch Pathologies Using Computational Fluid Dynamics
Abstract
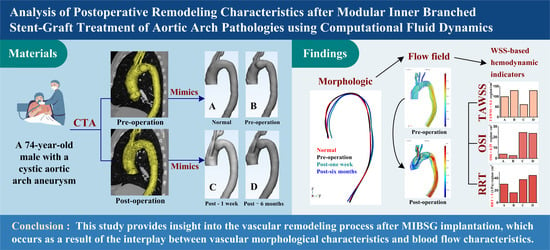
:1. Introduction
2. Materials and Methods
2.1. Image-Based Model Reconstruction
2.2. Computational Framework
2.3. Boundary Conditions
2.4. Related Indicators
3. Results
3.1. Morphological Description
3.2. Blood Perfusion
3.3. Hemodynamic Description
4. Discussion
5. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| AAPs | Aortic arch pathologies |
| CTA | Computed tomography angiography |
| IA | Innominate artery |
| LCCA | Left common carotid artery |
| RCCA | Right common carotid artery |
| LSA | Left subclavian artery |
| RSA | Right subclavian artery |
| MIBSG | Modular inner branched stent-graft |
| OSI | Oscillatory shear index |
| RRT | Relative residence time |
| TAWSS | Time-averaged wall shear stress |
| EVAR | Endovascular aortic repair |
| WSS | Wall shear stress |
References
- Kamman, A.V.; de Beaufort, H.W.L.; van Bogerijen, G.H.W.; Nauta, F.J.H.; Heijmen, R.H.; Moll, F.L.; van Herwaarden, J.A.; Trimarchi, S. Contemporary Management Strategies for Chronic Type B Aortic Dissections: A Systematic Review. PLoS ONE 2016, 11, e0154930. [Google Scholar] [CrossRef] [PubMed]
- Lioupis, C.; Abraham, C.Z. Results and Challenges for the Endovascular Repair of Aortic Arch Aneurysms. Perspect. Vasc. Surg. Endovasc. Ther. 2011, 23, 202–213. [Google Scholar] [CrossRef] [PubMed]
- Schenning, R.C.; Al-Hakim, R. Aortic Dissection: Branched, Fenestrated, and Parallel Aortic Stent Grafts in the Ascending Aorta and Arch. Tech. Vasc. Interv. Radiol. 2021, 24, 100754. [Google Scholar] [CrossRef]
- Manetta, F.; Newman, J.; Mattia, A. Indications for Thoracic EndoVascular Aortic Repair (TEVAR): A Brief Review. Int. J. Angiol. 2018, 27, 177–184. [Google Scholar] [CrossRef]
- Maurel, B.; Mastracci, T.M.; Spear, R.; Hertault, A.; Azzaoui, R.; Sobocinski, J.; Haulon, S. Branched and Fenestrated Options to Treat Aortic Arch Aneurysms. J. Cardiovasc. Surg. 2016, 57, 686–697. [Google Scholar]
- Blanco Amil, C.L.; Mestres Alomar, G.; Guarnaccia, G.; Luoni, G.; Yugueros Castellnou, X.; Chiara Vigliotti, R.; Ramses, R.; Riambau, V. The Initial Experience on Branched and Fenestrated Endografts in the Aortic Arch. A Systematic Review. Ann. Vasc. Surg. 2021, 75, 29–44. [Google Scholar] [CrossRef] [PubMed]
- Yuri, K.; Kimura, N.; Hori, D.; Yamaguchi, A.; Adachi, H. A Challenging Treatment for Aortic Arch Aneurysm with Fenestrated Stent Graft. Ann. Thorac. Surg. 2017, 104, 1915–1922. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hughes, G.C.; Vekstein, A. Current State of Hybrid Solutions for Aortic Arch Aneurysms. Ann. Cardiothorac. Surg. 2021, 10, 731–743. [Google Scholar] [CrossRef]
- Milne, C.P.E.; Haulon, S.; Oderich, G.S. Technical Aspects and Results of Branched Endografts for Repair of Aortic Arch Aneurysms. In Endovascular Aortic Repair: Current Techniques with Fenestrated, Branched and Parallel Stent-Grafts; Oderich, G.S., Ed.; Springer International Publishing: Cham, Switzerland, 2017; pp. 507–529. ISBN 978-3-319-15192-2. [Google Scholar]
- Inoue, K.; Hosokawa, H.; Iwase, T.; Sato, M.; Yoshida, Y.; Ueno, K.; Akiyoshi, T.; Terumitsu, T.; Shunichi, T.; Takahiko, S. Aortic Arch Reconstruction by Transluminally Placed Endovascular Branched Stent Graft. Circulation 1999, 100, II–316–II–321. [Google Scholar] [CrossRef]
- van Bakel, T.M.; de Beaufort, H.W.; Trimarchi, S.; Marrocco-Trischitta, M.M.; Bismuth, J.; Moll, F.L.; Patel, H.J.; van Herwaarden, J.A. Status of Branched Endovascular Aortic Arch Repair. Ann. Cardiothorac. Surg. 2018, 7, 406–413. [Google Scholar] [CrossRef] [Green Version]
- Hauck, S.R.; Kupferthaler, A.; Kern, M.; Rousseau, H.; Ferrer, C.; Iwakoshi, S.; Sakaguchi, S.; Stelzmuller, M.-E.; Ehrlich, M.; Loewe, C.; et al. Branched versus Fenestrated Thoracic Endovascular Aortic Repair in the Aortic Arch: A Multicenter Comparison. J. Thorac. Cardiovasc. Surg. 2022, 164, 1379–1389.e1. [Google Scholar] [CrossRef]
- Boufi, M.; Aouini, F.; Guivier-Curien, C.; Dona, B.; Loundou, A.D.; Deplano, V.; Alimi, Y.S. Examination of Factors in Type I Endoleak Development after Thoracic Endovascular Repair. J. Vasc. Surg. 2015, 61, 317–323. [Google Scholar] [CrossRef] [Green Version]
- Spear, R.; Haulon, S.; Ohki, T.; Tsilimparis, N.; Kanaoka, Y.; Milne, C.P.E.; Debus, S.; Takizawa, R.; Kölbel, T. Subsequent Results for Arch Aneurysm Repair with Inner Branched Endografts. J. Vasc. Surg. 2016, 63, 1129. [Google Scholar] [CrossRef]
- Kasprzak, P.M.; Mueller, T.; Loibnegger, A.; Kobuch, R.; Zorger, N.; Pfister, K. Fenestrated and Branched Stent Prostheses in the Aortic Arch: First Experiences. Gefasschirurgie 2009, 14, 198–205. [Google Scholar] [CrossRef]
- Simons, J.P.; Crawford, A.S.; Flanagan, C.P.; Aiello, F.A.; Arous, E.J.; Judelson, D.R.; Messina, L.M.; Robichaud, D.; Valliere, S.A.; Schanzer, A. Evolution of Fenestrated/Branched Endovascular Aortic Aneurysm Repair Complexity and Outcomes at an Organized Center for the Treatment of Complex Aortic Disease. J. Vasc. Surg. 2021, 73, 1148. [Google Scholar] [CrossRef]
- Wei, G.; Xin, J.; Yang, D.; Liu, X.; Tai, Y.; Zhang, H.; Liang, F.; Zhang, G. A New Modular Stent Graft to Reconstruct Aortic Arch. Eur. J. Vasc. Endovasc. Surg. 2009, 37, 560–565. [Google Scholar] [CrossRef] [Green Version]
- Guo, W.; Zhang, H.; Liu, X.; Ren, W.; Wang, Y. Endovascular Repair of Aortic Arch Aneurysm with a New Modular Double Inner Branch Stent Graft. Ann. Vasc. Surg. 2021, 77, 347.e1–347.e5. [Google Scholar] [CrossRef]
- Zhu, Y.; Li, F.; Zhang, H.; Song, H.; Ma, X.; Cao, L.; Zhang, W.; Guo, W. Hemodynamic Numerical Simulation of Aortic Arch Modular Inner Branched Stent-Graft in Eight Early Patients from the First-in-Human Case Series. Front. Cardiovasc. Med. 2022, 9, 981546. [Google Scholar] [CrossRef]
- van Bogerijen, G.H.W.; Auricchio, F.; Conti, M.; Lefieux, A.; Reali, A.; Veneziani, A.; Tolenaar, J.L.; Moll, F.L.; Rampoldi, V.; Trimarchi, S. Aortic Hemodynamics After Thoracic Endovascular Aortic Repair, With Particular Attention to the Bird-Beak Configuration. J. Endovasc. Ther. 2014, 21, 791–802. [Google Scholar] [CrossRef]
- Gallo, D.; Lefieux, A.; Morganti, S.; Veneziani, A.; Reali, A.; Auricchio, F.; Conti, M.; Morbiducci, U. A Patient-Specific Follow up Study of the Impact of Thoracic Endovascular Repair (TEVAR) on Aortic Anatomy and on Post-Operative Hemodynamics. Comput. Fluids 2016, 141, 54–61. [Google Scholar] [CrossRef]
- Etli, M.; Canbolat, G.; Karahan, O.; Koru, M. Numerical Investigation of Patient-Specific Thoracic Aortic Aneurysms and Comparison with Normal Subject via Computational Fluid Dynamics (CFD). Med. Biol. Eng. Comput. 2021, 59, 71–84. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Mei, Y.; Han, X.; Wei, J.; Watton, P.N.; Jia, W.; Li, A.; Chen, D.; Xiong, J. Optimization Schemes for Endovascular Repair with Parallel Technique Based on Hemodynamic Analyses. Int. J. Numer. Methods Biomed. Eng. 2019, 35, e3197. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nardi, A.; Even-Chen, B.; Avrahami, I. Experimental and Numerical Study of the Flow Dynamics in Treatment Approaches for Aortic Arch Aneurysms. In Aortic Aneurysm; IntechOpen: London, UK, 2017. [Google Scholar] [CrossRef] [Green Version]
- Qiao, Y.; Mao, L.; Ding, Y.; Fan, J.; Zhu, T.; Luo, K. Hemodynamic Consequences of TEVAR with in Situ Double Fenestrations of Left Carotid Artery and Left Subclavian Artery. Med. Eng. Phys. 2020, 76, 32–39. [Google Scholar] [CrossRef] [PubMed]
- Gur, H.B.; Halak, M.; Brand, M. Blood Flow in the Abdominal Aorta Post’ Chimney’ Endovascular Aneurysm Repair. In Proceedings of the 9th EUROSIM Congress on Modelling and Simulation, EUROSIM 2016, The 57th SIMS Conference on Simulation and Modelling SIMS2016, Oulu, Finland, 13–15 September 2016; pp. 667–672. [Google Scholar] [CrossRef]
- Liu, M.; Sun, A.; Deng, X. Hemodynamic Performance within Crossed Stent Grafts: Computational and Experimental Study on the Effect of Cross Position and Angle. BioMed. Eng. OnLine 2018, 17, 85. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Duraiswamy, N.; Schoephoerster, R.T.; Moreno, M.R.; Moore, J.E. Stented Artery Flow Patterns and Their Effects on the Artery Wall. Annu. Rev. Fluid Mech. 2007, 39, 357–382. [Google Scholar] [CrossRef]
- Numata, S.; Itatani, K.; Kanda, K.; Doi, K.; Yamazaki, S.; Morimoto, K.; Manabe, K.; Ikemoto, K.; Yaku, H. Blood Flow Analysis of the Aortic Arch Using Computational Fluid Dynamics. Eur. J. Cardio-Thorac. Surg. 2016, 49, 1578–1585. [Google Scholar] [CrossRef] [Green Version]
- Mirfendereski, S.; Park, J.S. Direct Numerical Simulation of a Pulsatile Flow in a Stenotic Channel Using Immersed Boundary Method. Eng. Rep. 2022, 4, e12444. [Google Scholar] [CrossRef]
- Chandran, K.B.; Rittgers, S.E.; Yoganathan, A.P. Biofluid Mechanics: The Human Circulation, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012; ISBN 978-1-4398-4516-5. [Google Scholar]
- Taylor, C.A.; Hughes, T.J.R.; Zarins, C.K. Effect of Exercise on Hemodynamic Conditions in the Abdominal Aorta. J. Vasc. Surg. 1999, 29, 1077–1089. [Google Scholar] [CrossRef] [Green Version]
- Malek, A.M. Hemodynamic Shear Stress and Its Role in Atherosclerosis. JAMA 1999, 282, 2035. [Google Scholar] [CrossRef]
- Qiao, Y.; Fan, J.; Ding, Y.; Zhu, T.; Luo, K. A Primary Computational Fluid Dynamics Study of Pre- and Post-TEVAR With Intentional Left Subclavian Artery Coverage in a Type B Aortic Dissection. J. Biomech. Eng.-Trans. Asme 2019, 141, 111002. [Google Scholar] [CrossRef]
- Tseng, F.S.; Soong, T.K.; Syn, N.; Ong, C.W.; Liang, L.H.; Choong, A. Computational Fluid Dynamics in Complex Aortic Surgery: Applications, Prospects and Challenges. J. Surg. Simul. 2017, 4, 1–4. [Google Scholar] [CrossRef]
- Tran, K.; Kaladji, A.; Yang, W.; Marsden, A.L.; Lee, J. Patient-Specific Computational Flow Simulation Reveals Differences in Aortic Hemodynamics Between Two versus Four Vessel Fenestrated Endovascular Aneurysm Repair. Circulation 2021, 144, A13545. [Google Scholar] [CrossRef]
- Auricchio, F.; Conti, M.; Lefieux, A.; Morganti, S.; Reali, A.; Sardanelli, F.; Secchi, F.; Trimarchi, S.; Veneziani, A. Patient-Specific Analysis of Post-Operative Aortic Hemodynamics: A Focus on Thoracic Endovascular Repair (TEVAR). Comput. Mech. 2014, 54, 943–953. [Google Scholar] [CrossRef]
- Midulla, M.; Moreno, R.; Negre-Salvayre, A.; Beregi, J.-P.; Haulon, S.; Loffroy, R.; Dake, M.; Rousseau, H. Impact of Thoracic Endografting on the Hemodynamics of the Native Aorta: Pre- and Postoperative Assessments of Wall Shear Stress and Vorticity Using Computational Fluid Dynamics. J. Endovasc. Ther. 2021, 28, 63–69. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Li, Z.; Dong, H.; Zhang, Y.; Wei, J.; Watton, P.N.; Guo, W.; Chen, D.; Xiong, J. Hemodynamic Parameters That May Predict False-Lumen Growth in Type-B Aortic Dissection after Endovascular Repair: A Preliminary Study on Long-Term Multiple Follow-Ups. Med. Eng. Phys. 2017, 50, 12–21. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dottori, J.; Casciaro, M.; Craiem, D.; El-Batti, S.; Mousseaux, E.; Alsac, J.-M.; Larrabide, I. Regional Assessment of Vascular Morphology and Hemodynamics: Methodology and Evaluation for Abdominal Aortic Aneurysms after Endovascular Repair. Comput. Methods Biomech. Biomed. Eng. 2020, 23, 1060–1070. [Google Scholar] [CrossRef]
- Stefanov, F.; McGloughlin, T.; Morris, L. A Computational Assessment of the Hemodynamic Effects of Crossed and Non-Crossed Bifurcated Stent-Graft Devices for the Treatment of Abdominal Aortic Aneurysms. Med. Eng. Phys. 2016, 38, 1458–1473. [Google Scholar] [CrossRef]
- Kokkalis, E.; Aristokleous, N.; Houston, J.G. Haemodynamics and Flow Modification Stents for Peripheral Arterial Disease: A Review. Ann. Biomed. Eng. 2016, 44, 466–476. [Google Scholar] [CrossRef] [Green Version]
- Arab, M.I.; Bouzit, M.; Ameur, H.; Kamla, Y. Numerical Study on Thoracic Aortic Aneurysms: The Aneurysm Aggravation Effects on the Secondary Flow Motion. Mechanics 2020, 26, 407–415. [Google Scholar] [CrossRef]
- Matsuzawa, T.; Gao, F.; Qiao, A.; Ohta, O.; Okada, H. Numerical Simulation in Aortic Arch Aneurysm. Etiol. Pathog. Pathophysiol. Aortic Aneurysms Aneurysm Rupture 2011, 12, 208–222. [Google Scholar] [CrossRef] [Green Version]
- Qiao, A.-K.; Fu, W.-Y.; Liu, Y.-J. Study on Hemodynamics in Patient-Specific Thoracic Aortic Aneurysm. Theor. Appl. Mech. Lett. 2011, 1, 14001. [Google Scholar] [CrossRef] [Green Version]
- Rolland, P.H.; Charifi, A.-B.; Verrier, C.; Bodard, H.; Friggi, A.; Piquet, P.; Moulin, G.; Bartoli, J.-M. Hemodynamics and Wall Mechanics after Stent Placement in Swine Iliac Arteries: Comparative Results from Six Stent Designs1. Radiology 1999, 213, 229–246. [Google Scholar] [CrossRef] [PubMed]
- Moore, J.E.; Berry, J.L. Fluid and Solid Mechanical Implications of Vascular Stenting. Ann. Biomed. Eng. 2002, 30, 498–508. [Google Scholar] [CrossRef] [PubMed]
- Nardi, A.; Avrahami, I. Approaches for Treatment of Aortic Arch Aneurysm, a Numerical Study. J. Biomech. 2017, 50, 158–165. [Google Scholar] [CrossRef]
- Romarowski, R.M.; Conti, M.; Morganti, S.; Grassi, V.; Marrocco-Trischitta, M.M.; Trimarchi, S.; Auricchio, F. Computational Simulation of TEVAR in the Ascending Aorta for Optimal Endograft Selection: A Patient-Specific Case Study. Comput. Biol. Med. 2018, 103, 140–147. [Google Scholar] [CrossRef]
- Qiao, Y.; Mao, L.; Zhu, T.; Fan, J.; Luo, K. Biomechanical Implications of the Fenestration Structure after Thoracic Endovascular Aortic Repair. J. Biomech. 2020, 99, 109478. [Google Scholar] [CrossRef]
- Mestres, G.; Garcia, M.E.; Yugueros, X.; Urrea, R.; Tripodi, P.; Gomez, F.; Maeso, J.; Riambau, V. Aortic Arch and Thoracic Aorta Curvature Remodeling after Thoracic Endovascular Aortic Repair. Ann. Vasc. Surg. 2017, 38, 233–241. [Google Scholar] [CrossRef]
- Hirotsu, K.; Suh, G.-Y.; Lee, J.T.; Dake, M.D.; Fleischmann, D.; Cheng, C.P. Changes in Geometry and Cardiac Deformation of the Thoracic Aorta after Thoracic Endovascular Aortic Repair. Ann. Vasc. Surg. 2018, 46, 83–89. [Google Scholar] [CrossRef]
- Fung, G.S.K.; Lam, S.K.; Cheng, S.W.K.; Chow, K.W. On Stent-Graft Models in Thoracic Aortic Endovascular Repair: A Computational Investigation of the Hemodynamic Factors. Comput. Biol. Med. 2008, 38, 484–489. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Zhu, Y.; Song, H.; Zhang, H.; Chen, L.; Guo, W. Analysis of Postoperative Remodeling Characteristics after Modular Inner Branched Stent-Graft Treatment of Aortic Arch Pathologies Using Computational Fluid Dynamics. Bioengineering 2023, 10, 164. https://doi.org/10.3390/bioengineering10020164
Li F, Zhu Y, Song H, Zhang H, Chen L, Guo W. Analysis of Postoperative Remodeling Characteristics after Modular Inner Branched Stent-Graft Treatment of Aortic Arch Pathologies Using Computational Fluid Dynamics. Bioengineering. 2023; 10(2):164. https://doi.org/10.3390/bioengineering10020164
Chicago/Turabian StyleLi, Fen, Yating Zhu, Hui Song, Hongpeng Zhang, Lingfeng Chen, and Wei Guo. 2023. "Analysis of Postoperative Remodeling Characteristics after Modular Inner Branched Stent-Graft Treatment of Aortic Arch Pathologies Using Computational Fluid Dynamics" Bioengineering 10, no. 2: 164. https://doi.org/10.3390/bioengineering10020164
APA StyleLi, F., Zhu, Y., Song, H., Zhang, H., Chen, L., & Guo, W. (2023). Analysis of Postoperative Remodeling Characteristics after Modular Inner Branched Stent-Graft Treatment of Aortic Arch Pathologies Using Computational Fluid Dynamics. Bioengineering, 10(2), 164. https://doi.org/10.3390/bioengineering10020164