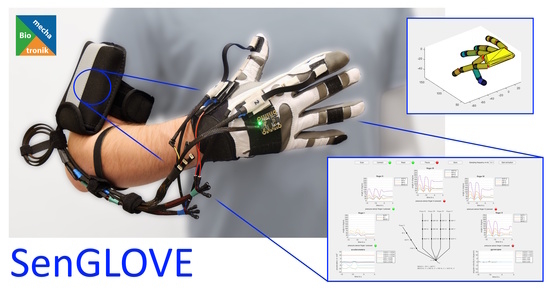
SenGlove—A Modular Wearable Device to Measure Kinematic Parameters of The Human Hand
Abstract
:1. Introduction
1.1. Overview
1.2. Related Work
1.3. Our Contribution
2. Materials and Methods
2.1. Basic Assumptions and Requirements/Aims of the Design
2.2. Simplified Hand Model
2.3. Denavit–Hartenberg Method
- Joint angle of the joint axis describes the angle of rotation from the axis to the axis around the axis .
- Joint distance describes the translation of the origin of the coordinate system along the axis so that the distance between the origins of and becomes minimal.
- Link length describes the translation of the origin of the coordinate system along the axis so that the distance between the origins of and becomes minimal.
- Link twist angle describes the angle of rotation from the axis to the axis around the axis .
2.4. Hand Size Examination
2.5. Measurement Parameters
2.6. Sensor Concept
2.7. Mechanical Structure
2.8. Electronic Structure
- Microcontroller (Arduino Nano® RP2040 Connect);
- Bluetooth® module (HC-06);
- Pressure sensors (Interlink Electronics® FSR 400 Short);
- IMU sensor (Adafruit® 9-DOF Orientation IMU BNO085);
- Low current lithium-ion battery pack (Tenergy® 51126).
2.9. Software
2.10. Validation Method
2.10.1. Measurement Accuracy
2.10.2. Runtime
3. Results
3.1. Final Design
3.2. Power Consumption and Mass
3.3. Measurement Accuracy and Runtime
3.4. Variants of Visualization
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADC | Analog–Digital Converter |
| BLE | Bluetooth® Low Energy |
| CMC | Carpometacarpal |
| DH | Denavit–Hartenberg |
| DIP | Distal Interphalangeal |
| DOAJ | Directory of Open Access Journals |
| DoF | Degrees of Freedom |
| FSR | Force Sensing Resistor |
| GUI | Graphical User Interface |
| IDE | Integrated Development Environment |
| IMU | Inertial Measurement Unit |
| IP | Interphalangeal |
| MCP | Metacarpophalangeal |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MUX | Multiplexer |
| PC | Personal Computer |
| PIP | Proximal Interphalangeal |
| USB | Universal Serial Bus |
| VDI | Verein Deutscher Ingenieure |
Appendix A. Design Variants


Appendix B. Finger Anthropometry
| Finger Length of the Extended Middle Finger | |||||
|---|---|---|---|---|---|
| 1st Percentile | 5th Percentile | 50th Percentile | 95th Percentile | 99th Percentile | |
| Men | 102.0 mm | 105.0 mm | 114.0 mm | 123.0 mm | 127.0 mm |
| Women | 89.0 mm | 92.0 mm | 101.0 mm | 110.0 mm | 114.0 mm |
| Range of Motion of the Finger Joints | |
|---|---|
| Flexion/Extension | Finger II to V |
| MCP | 90°/0°/45° |
| PIP | 110°/0°/0° |
| DIP | 80°/0°/5° |
| Radii of the Middle Finger Joints and Resulting Increase in Length | |||||
|---|---|---|---|---|---|
| Men | |||||
| Joint radius | 1st percentile | 5th percentile | 50th percentile | 95th percentile | 99th percentile |
| MCP | 14.0 mm | 14.7 mm | 16.5 mm | 18.3 mm | 19.0 mm |
| PIP | 8.5 mm | 8.9 mm | 10.0 mm | 11.1 mm | 11.5 mm |
| DIP | 6.5 mm | 6.9 mm | 8.0 mm | 9.1 mm | 9.5 mm |
| Increase in length | 1st percentile | 5th percentile | 50th percentile | 95th percentile | 99th percentile |
| MCP | 22.0 mm | 23.1 mm | 25.9 mm | 28.7 mm | 29.8 mm |
| PIP | 16.3 mm | 17.1 mm | 19.2 mm | 21.3 mm | 22.1 mm |
| DIP | 9.1 mm | 9.6 mm | 11.2 mm | 12.7 mm | 13.3 mm |
| Women | |||||
| Joint radius | 1st percentile | 5th percentile | 50th percentile | 95th percentile | 99th percentile |
| MCP | 12.0 mm | 12.6 mm | 14.0 mm | 15.4 mm | 16.0 mm |
| PIP | 7.5 mm | 7.8 mm | 8.5 mm | 9.2 mm | 9.5 mm |
| DIP | 5.5 mm | 5.8 mm | 6.5 mm | 7.2 mm | 8.0 mm |
| Increase in length | 1st percentile | 5th percentile | 50th percentile | 95th percentile | 99th percentile |
| MCP | 18.8 mm | 19.8 mm | 22.0 mm | 24.2 mm | 25.1 mm |
| PIP | 14.4 mm | 15.0 mm | 16.3 mm | 17.7 mm | 18.2 mm |
| DIP | 7.7 mm | 8.1 mm | 9.1 mm | 10.1 mm | 11.2 mm |
| Total Length of Skin (Middle Finger, Maximum Flexion) | |||||
|---|---|---|---|---|---|
| 1st Percentile | 5th Percentile | 50th Percentile | 95th Percentile | 99th Percentile | |
| Men | 149.4 mm | 154.8 mm | 170.3 mm | 185.5 mm | 192.2 mm |
| Women | 129.9 mm | 134.9 mm | 148.4 mm | 161.9 mm | 168.5 mm |
| Distance between the PIP and DIP joint (Extended Middle Finger) | |||||
|---|---|---|---|---|---|
| 1st Percentile | 5th Percentile | 50th Percentile | 95th Percentile | 99th Percentile | |
| Men | 59.2 ± 3.6 mm | 60.9 ± 3.7 mm | 66.1 ± 4.0 mm | 71.3 ± 4.3 mm | 73.7 ± 4.5 mm |
| Women | 51.6 ± 3.1 mm | 53.4 ± 3.2 mm | 58.6 ± 3.5 mm | 63.8 ± 3.9 mm | 66.1 ± 4.0 mm |
| Distance between the PIP and DIP Joint (Flexed Middle Finger) | |||||
|---|---|---|---|---|---|
| 1st Percentile | 5th Percentile | 50th Percentile | 95th Percentile | 99th Percentile | |
| Men | 97.5 ± 3.6 mm | 101.1 ± 3.7 mm | 111.2 ± 4.0 mm | 121.3 ± 4.3 mm | 125.6 ± 4.5 mm |
| Women | 84.8 ± 3.1 mm | 88.2 ± 3.2 mm | 96.9 ± 3.5 mm | 105.7 ± 3.9 mm | 109.4 ± 4.0 mm |
Appendix C. Denavit–Hartenberg Parameters
| Denavit -Hartenberg Parameters | ||||
|---|---|---|---|---|
| Joint ji | ||||
| 0 | 0° | |||
| 0 | 0° | |||
| 0 | 0° | |||
Appendix D. Validation Setup

Appendix E. Measurement Accuracy of Finger I

| Measurement Accuracy at Finger I | |||
|---|---|---|---|
| Measurement series | |||
| Parameter | MCP joint | IP joint | MCP a. IP joint |
| 1° | 1.69° | 1.69° | |
| 0° | −0.31° | −0.31° | |
| RMSE | 0.56° | 0.71° | 0.64° |
| Measurement series | |||
| Parameter | MCP joint | IP joint | MCP a. IP joint |
| 2° | 3.01° | 3.01° | |
| −3° | −1.27° | −3° | |
| RMSE | 0.66° | 1.00° | 0.84° |
| Measurement series | |||
| Parameter | MCP joint | IP joint | MCP a. IP joint |
| 2° | 3.79° | 3.79° | |
| −3° | −1.71° | −3° | |
| RMSE | 1.08° | 1.21° | 1.15° |
| Measurement series | |||
| Parameter | MCP joint | IP joint | MCP a. IP joint |
| 1° | 2.76° | 2.76° | |
| −2° | −2.18° | −2.18° | |
| RMSE | 0.97° | 1.22° | 1.10° |
| Measurement series | |||
| Parameter | MCP joint | IP joint | MCP a. IP joint |
| 1° | 3.03° | 3.03° | |
| −3° | −2.20° | −2.20° | |
| RMSE | 1.19° | 1.10° | 1.14° |
| Measurement series | |||
| Parameter | MCP joint | IP joint | MCP a. IP joint |
| 1° | 2.23° | 2.23° | |
| −2° | −2.34° | −2.34° | |
| RMSE | 1.13° | 0.87° | 1.01° |
| Measured values of all measurement series | |||
| Parameter | MCP joint | IP joint | MCP a. IP joint |
| 2° | 3.79° | 3.79° | |
| −3° | −2.34° | −3° | |
| RMSE | 0.96° | 1.03° | 0.99° |
Appendix F. Measurement Accuracy of Finger II

| Measurement Accuracy at Finger II | ||||
|---|---|---|---|---|
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 2° | 2.55° | 3.85° | 3.85° | |
| −1° | −16.06° | −5.42° | −16.06° | |
| RMSE | 0.46° | 1.15° | 2.43° | 1.57° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 3° | 2.90° | 4.87° | 4.87° | |
| −2° | −1.91° | −4.87° | −4.87° | |
| RMSE | 1.00° | 1.18° | 2.60° | 1.75° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 2° | 1.76° | 4.23° | 4.23° | |
| −2° | −1.05° | −5.57° | −5.57° | |
| RMSE | 0.71° | 0.81° | 2.25° | 1.44° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 2° | 1.54° | 4.36° | 4.36° | |
| −1° | −1.52° | −5.67° | −5.67° | |
| RMSE | 0.64° | 0.62° | 2.30° | 1.43° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 1.85° | 3.97° | 3.97° | |
| −1° | −1.42° | −5.15° | −5.15° | |
| RMSE | 0.65° | 0.81° | 2.24° | 1.42° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 2.15° | 4.30° | 4.30° | |
| −1° | −1.00° | −5.67° | −5.67° | |
| RMSE | 0.57° | 0.71° | 2.36° | 1.46° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 2° | 1.99° | 4.36° | 4.36° | |
| −2° | −3.93° | −5.11° | −5.11° | |
| RMSE | 0.89° | 0.92° | 2.49° | 1.62° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 1.71° | 4.05° | 4.05° | |
| −1° | −0,77° | 1,16° | −1° | |
| RMSE | 0.61° | 0.55° | 2.79° | 1.68° |
| Measured values of all measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 3° | 2.90° | 4.87° | 4.87° | |
| −2° | −16,06° | −5.67° | −16.06° | |
| RMSE | 0.72° | 0.90° | 2.39° | 1.53° |
Appendix G. Measurement Accuracy of Finger III

| Measurement accuracy of finger III | ||||
|---|---|---|---|---|
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 0.92° | 3.84° | 3.84° | |
| 0° | −1.51° | −5.13° | −5.13° | |
| RMSE | 0.04° | 1.30° | 2.51° | 1.46° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 1.65° | 4.44° | 4.44° | |
| −1° | −1.40° | −5.68° | −5.68° | |
| RMSE | 0,20° | 0.47° | 2.44° | 1.44° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 1.23° | 3.63° | 3.63° | |
| −1° | −1.38° | −5.92° | −5.92° | |
| RMSE | 0.20° | 0.39° | 2.18° | 1.28° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 1.20° | 4.02° | 4.02° | |
| −1° | −1.28° | −5.52° | −5.52° | |
| RMSE | 0.35° | 0.44° | 2.12° | 1.27° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 2.64° | 3.63° | 3.63° | |
| −1° | −1.62° | −5.11° | −5.11° | |
| RMSE | 0.38° | 0.62° | 2.12° | 1.29° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 2.26° | 4.05° | 4.05° | |
| −1° | −1.31° | −5.27° | −5.27° | |
| RMSE | 0.50° | 0.68° | 2.19° | 1.36° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 1.55° | 4.05° | 4.05° | |
| −1° | −1.21° | −4.99° | −4.99° | |
| RMSE | 0.26° | 0.48° | 2.18° | 1.30° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 0° | 1.74° | 3.85° | 3.85° | |
| −1° | −0.50° | −5.28° | −5.28° | |
| RMSE | 0.33° | 0.57° | 2.69° | 1.60° |
| Measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 0° | 1,85° | −3.76° | 1.85° | |
| −2° | −0.15° | −5.10° | −5.10° | |
| RMSE | 0.47° | 0.46° | 4.87° | 2.83° |
| Measured values of all measurement series | ||||
| Parameter | MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint |
| 1° | 2.64° | 4.44° | 4.44° | |
| −2° | −1.62° | −5.92° | −5.92° | |
| RMSE | 0.32° | 0.50° | 2.34° | 2.38° |
Appendix H. Fully Sensorized Wearable

References
- Hirt, B.; Seyhan, H.; Wagner, M.; Zumhasch, R. Anatomie und Biomechanik der Hand; Georg Thieme Verlag: Stuttgart, Germany, 2014. [Google Scholar]
- Wood, B.; Collard, M. The Meaning of Homo. Ludus Vitalis 2001, 9, 63–74. [Google Scholar]
- Zaman, S.u.; Tao, X.; Cochrane, C.; Koncar, V. Smart E-Textile Systems: A Review for Healthcare Applications. Electronics 2022, 11, 99. [Google Scholar] [CrossRef]
- Chakarov, D.; Veneva, I.; Tsveov, M. A New Upper Limb Exoskeleton for Human Interaction with Virtual Enviroments and Rehabilitation Tasks. In Proceedings of the 10th International Conference Mechatronic Systems and Materials (MSM 2014), Opole, Poland, 7–10 July 2014. [Google Scholar]
- Tawk, C.; in het Panhuis, M.; Spinks, G.M.; Alici, G. Soft Pneumatic Sensing Chambers for Generic and Interactive Human–Machine Interfaces. Adv. Intell. Syst. 2019, 1, 1900002. [Google Scholar] [CrossRef] [Green Version]
- Sun, Z.; Zhu, M.; Lee, C. Progress in the Triboelectric Human–Machine Interfaces (HMIs)-Moving from Smart Gloves to AI/Haptic Enabled HMI in the 5G/IoT Era. Nanoenergy Adv. 2021, 1, 81–120. [Google Scholar] [CrossRef]
- Abad, A.C.; Reid, D.; Ranasinghe, A. A Novel Untethered Hand Wearable with Fine-Grained Cutaneous Haptic Feedback. Sensors 2022, 22, 1924. [Google Scholar] [CrossRef]
- Balasubramanian, S.; Klein, J.; Burdet, E. Robot-assisted rehabilitation of hand function. Curr. Opin. Neurol. 2010, 23, 661–670. [Google Scholar] [CrossRef]
- Delph, M.A.; Fischer, S.A.; Gauthier, P.W.; Luna, C.H.M.; Clancy, E.A.; Fischer, G.S. A soft robotic exomusculature glove with integrated sEMG sensing for hand rehabilitation. In Proceedings of the 2013 IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013; pp. 1–7. [Google Scholar]
- Lambercy, O.; Ranzani, R.; Gassert, R. Chapter 15—Robot-assisted rehabilitation of hand function. In Rehabilitation Robotics; Colombo, R., Sanguineti, V., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 205–225. [Google Scholar] [CrossRef]
- Semprini, M.; Cuppone, A.; Squeri, V.; Konczak, J. Muscle innervation patterns for human wrist control: Useful biofeedback signals for robotic rehabilitation? In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015; pp. 919–924. [Google Scholar] [CrossRef]
- Duanmu, D.; Wang, X.; Li, X.; Wang, Z.; Hu, Y. Design of Guided Bending Bellows Actuators for Soft Hand Function Rehabilitation Gloves. Actuators 2022, 11, 346. [Google Scholar] [CrossRef]
- Xia, K.; Chen, X.; Chang, X.; Liu, C.; Guo, L.; Xu, X.; Lv, F.; Wang, Y.; Sun, H.; Zhou, J. Hand Exoskeleton Design and Human-Machine Interaction Strategies for Rehabilitation. Bioengineering 2022, 9, 682. [Google Scholar] [CrossRef]
- Zhou, Z.; Chen, K.; Li, X.; Zhang, S.; Wu, Y.; Zhou, Y.; Meng, K.; Sun, C.; He, Q.; Fan, W.; et al. Sign-to-speech translation using machine-learning-assisted stretchable sensor arrays. Nat. Electron. 2020, 3, 571–578. [Google Scholar] [CrossRef]
- Allela, R.; Muthoni, C.; Karibe, D. Sign-IO. 2019. Available online: http://www.sign-io.com (accessed on 31 January 2023).
- Chen, X.; Gong, L.; Wei, L.; Yeh, S.C.; Da Xu, L.; Zheng, L.; Zou, Z. A Wearable Hand Rehabilitation System With Soft Gloves. IEEE Trans. Ind. Inform. 2021, 17, 943–952. [Google Scholar] [CrossRef]
- Korzeniewska, E.; Kania, M.; Zawiślak, R. Textronic Glove Translating Polish Sign Language. Sensors 2022, 22, 6788. [Google Scholar] [CrossRef] [PubMed]
- Ji, L.; Liu, J.; Shimamoto, S. Recognition of Japanese Sign Language by Sensor-Based Data Glove Employing Machine Learning. In Proceedings of the 2022 IEEE 4th Global Conference on Life Sciences and Technologies (LifeTech), Osaka, Japan, 7–9 March 2022; pp. 256–258. [Google Scholar] [CrossRef]
- Lee, M.; Bae, J. Real-Time Gesture Recognition in the View of Repeating Characteristics of Sign Languages. IEEE Trans. Ind. Inform. 2022, 18, 8818–8828. [Google Scholar] [CrossRef]
- Sharma, S.; Singh, S. Vision-based hand gesture recognition using deep learning for the interpretation of sign language. Expert Syst. Appl. 2021, 182, 115657. [Google Scholar] [CrossRef]
- Dipietro, L.; Sabatini, A.M.; Dario, P. A Survey of Glove-Based Systems and Their Applications. IEEE Trans. Syst. Man, Cybern. Part C 2008, 38, 461–482. [Google Scholar] [CrossRef]
- Ramos, O.; Múnera, M.; Moazen, M.; Wurdemann, H.; Cifuentes, C.A. Assessment of Soft Actuators for Hand Exoskeletons: Pleated Textile Actuators and Fiber-Reinforced Silicone Actuators. Front. Bioeng. Biotechnol. 2022, 10. [Google Scholar] [CrossRef]
- Kim, G.; Vu, C.C.; Kim, J. Single-Layer Pressure Textile Sensors with Woven Conductive Yarn Circuit. Appl. Sci. 2020, 10, 2877. [Google Scholar] [CrossRef]
- Nakajima, T.; Asami, Y.; Endo, Y.; Tada, M.; Ogihara, N. Prediction of anatomically and biomechanically feasible precision grip posture of the human hand based on minimization of muscle effort. Sci. Rep. 2022, 12. [Google Scholar] [CrossRef]
- Leonardis, D.; Barsotti, M.; Loconsole, C.; Solazzi, M.; Troncossi, M.; Mazzotti, C.; Castelli, V.P.; Procopio, C.; Lamola, G.; Chisari, C.; et al. An EMG-Controlled Robotic Hand Exoskeleton for Bilateral Rehabilitation. IEEE Trans. Haptics 2015, 8, 140–151. [Google Scholar] [CrossRef]
- Erol, A.; Bebis, G.; Nicolescu, M.; Boyle, R.; Twombly, X. Vision-based hand pose estimation: A review. Comput. Vis. Image Underst. 2007, 108, 52–73. [Google Scholar] [CrossRef]
- Mohamed, N.; Mustafa, M.B.; Jomhari, N. A Review of the Hand Gesture Recognition System: Current Progress and Future Directions. IEEE Access 2021, 9, 157422–157436. [Google Scholar] [CrossRef]
- Nishiyama, M.; Watanabe, K. Wearable Sensing Glove With Embedded Hetero-Core Fiber-Optic Nerves for Unconstrained Hand Motion Capture. IEEE Trans. Instrum. Meas. 2009, 58, 3995–4000. [Google Scholar] [CrossRef]
- Dipietro, L.; Sabatini, A.M.; Dario, P. Evaluation of an instrumented glove for hand-movement acquisition. J. Rehabil. Res. Dev. 2003, 40 2, 179–189. [Google Scholar] [CrossRef]
- Chang, H.T.; Chang, J.Y. Sensor Glove Based on Novel Inertial Sensor Fusion Control Algorithm for 3-D Real-Time Hand Gestures Measurements. IEEE Trans. Ind. Electron. 2020, 67, 658–666. [Google Scholar] [CrossRef]
- Kortier, H.G.; Sluiter, V.I.; Roetenberg, D.; Veltink, P.H. Assessment of hand kinematics using inertial and magnetic sensors. J. Neuroeng. Rehabil. 2013, 11, 70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, B.S.; Lee, I.J.; Yang, S.Y.; Lo, Y.C.; Lee, J.; Chen, J.L. Design of an Inertial-Sensor-Based Data Glove for Hand Function Evaluation. Sensors 2018, 18, 1545. [Google Scholar] [CrossRef] [Green Version]
- Hsiao, P.C.; Yang, S.Y.; Lin, B.S.; Lee, I.J.; Chou, W. Data glove embedded with 9-axis IMU and force sensing sensors for evaluation of hand function. In Proceedings of the 2015 37th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Milano, Italy, 25–29 August 2015; pp. 4631–4634. [Google Scholar] [CrossRef]
- Saggio, G.; Bocchetti, S.; Pinto, C.A.; Orengo, G.; Giannini, F. A novel application method for wearable bend sensors. In Proceedings of the 2009 2nd International Symposium on Applied Sciences in Biomedical and Communication Technologies, Bratislava, Slovak Republic, 24–27 November 2009; pp. 1–3. [Google Scholar] [CrossRef]
- Polygerinos, P.; Wang, Z.; Galloway, K.C.; Wood, R.J.; Walsh, C.J. Soft robotic glove for combined assistance and at-home rehabilitation. Robot. Auton. Syst. 2015, 73, 135–143. [Google Scholar] [CrossRef] [Green Version]
- Yap, H.K.; Ang, B.W.K.; Lim, J.H.; Goh, J.C.H.; Yeow, C.H. A fabric-regulated soft robotic glove with user intent detection using EMG and RFID for hand assistive application. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 3537–3542. [Google Scholar] [CrossRef]
- Stoppa, M.; Chiolerio, A. Wearable Electronics and Smart Textiles: A Critical Review. Sensors 2014, 14, 11957–11992. [Google Scholar] [CrossRef] [Green Version]
- Huang, C.T.; Shen, C.L.; Tang, C.F.; Chang, S.H. A wearable yarn-based piezo-resistive sensor. Sensors Actuators Phys. 2008, 141, 396–403. [Google Scholar] [CrossRef]
- Aumüller, G.; Aust, G.; Conrad, A.; Engele, J.; Kirsch, J. Duale Reihe Anatomie; Duale Reihe, Georg Thieme Verlag: Stuttgard, Germany, 2017. [Google Scholar]
- Witte, H.; Schilling, C. The concept of biomechatronic systems as a means to support the development of biosensors. Int. J. Biosens. Bioelectron. 2017, 2, 114–115. [Google Scholar] [CrossRef] [Green Version]
- (VDI), V.D.I. Entwicklungsmethodik für Mechatronische Systeme (VDI 2206): Design Methodology for Mechatronic Systems; Beuth Verlag: Berlin, Germany, 2004. [Google Scholar]
- National Research Council. Virtual Reality: Scientific and Technological Challenges; Durlach, N.I., Mavor, A.S., Eds.; The National Academies Press: Washington, DC, USA, 1995. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Zhang, X.; Wang, K.; Wang, Z.J. A Sign-Component-Based Framework for Chinese Sign Language Recognition Using Accelerometer and sEMG Data. IEEE Trans. Biomed. Eng. 2012, 59, 2695–2704. [Google Scholar] [CrossRef]
- Weber, W. Industrieroboter: Methoden der Steuerung und Regelung; Carl Hanser Verlag GmbH & Co. KG: Munich, Germany, 2019. [Google Scholar]
- Park, Y.; Lee, J.; Bae, J. Development of a Wearable Sensing Glove for Measuring the Motion of Fingers Using Linear Potentiometers and Flexible Wires. IEEE Trans. Ind. Inform. 2015, 11, 198–206. [Google Scholar] [CrossRef]
- Tilley, A.; Associates, H. The Measure of Man and Woman: Human Factors in Design; Interior Design Industrial Design; Wiley: New York, NY, USA, 2002. [Google Scholar]
- Burfeind, H. Zur Biomechanik des Fingers unter Berücksichtigung der Krümmungsinkongruenz der Gelenkflächen; Cuvillier: Göttingen, Germany, 2004. [Google Scholar]
- de Monsabert, B.G.; Visser, J.M.A.; Vigouroux, L.; Van der Helm, F.C.T.; Veeger, H.E.J. Comparison of three local frame definitions for the kinematic analysis of the fingers and the wrist. J. Biomech. 2014, 47, 2590–2597. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chao, E.; An, K.; Conney, W.; Linscheid, R. Biomechanics of the Hand: A Basic Research Study; World Scientific Publishing Company: Singapore, 1989. [Google Scholar]
- Bionic Gloves | ReliefGrip™ Golf Gloves. 2021. Available online: https://www.bionicgloves.com/reliefgrip?quantity=1&custcol3=14 (accessed on 31 January 2023).
- Malvezzi, M.; Gioioso, G.; Salvietti, G.; Prattichizzo, D. SynGrasp: A MATLAB Toolbox for Underactuated and Compliant Hands. IEEE Robot. Autom. Mag. 2015, 22, 52–68. [Google Scholar] [CrossRef]
- Hill, J. Do deaf communities actually want sign language gloves? Nat. Electron. 2020, 3. [Google Scholar] [CrossRef]
- Novak, D.; Riener, R. A survey of sensor fusion methods in wearable robotics. Robot. Auton. Syst. 2015, 73, 155–170. [Google Scholar] [CrossRef]
- Barsoum, E. Articulated Hand Pose Estimation Review. CoRR 2016, arXiv:1604.06195. [Google Scholar]
- Dong, W.; Yang, L.; Gravina, R.; Fortino, G. Soft Wrist-Worn Multi-Functional Sensor Array for Real-Time Hand Gesture Recognition. IEEE Sensors J. 2022, 22, 17505–17514. [Google Scholar] [CrossRef]
- Jiang, S.; Li, L.; Xu, H.; Xu, J.; Gu, G.; Shull, P.B. Stretchable e-Skin Patch for Gesture Recognition on the Back of the Hand. IEEE Trans. Ind. Electron. 2020, 67, 647–657. [Google Scholar] [CrossRef]
- Li, L.; Jiang, S.; Shull, P.B.; Gu, G. SkinGest: Artificial skin for gesture recognition via filmy stretchable strain sensors. Adv. Robot. 2018, 32, 1112–1121. [Google Scholar] [CrossRef]
- Takada, R.; Kadomoto, J.; Shizuki, B. A Sensing Technique for Data Glove Using Conductive Fiber. In Proceedings of the Extended Abstracts of the 2019 CHI Conference on Human Factors in Computing Systems, Glasgow, UK, 4–9 May 2019; Association for Computing Machinery: New York, NY, USA; pp. 1–4. [Google Scholar] [CrossRef]












| Finger | Measurement Parameter |
|---|---|
| I..V | flexion-/extension angle MCP joint |
| (condition touching the palm with fingertip) | |
| I | flexion-/extension angle IP joint |
| (condition opposition position of finger I) | |
| II..V | flexion-/extension angle PIP joint |
| flexion-/extension angle DIP joint | |
| Hand | Measurement Parameter |
| back of hand | absolute orientation/rotation vector |
| (angular velocity in three axes) | |
| (linear acceleration in three axes) |
| Root-Mean-Square Error | ||||
|---|---|---|---|---|
| MCP joint | IP joint | MCP a. IP joint | ||
| Finger I | 0,96 | 1,03 | 0,99 | |
| MCP joint | PIP joint | DIP joint | MCP, PIP a. DIP joint | |
| Finger II | 0,72 | 0,90 | 2,39 | 1,53 |
| Finger III | 0,32 | 0,50 | 2,34 | 2,38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
David, J.P.; Helbig, T.; Witte, H. SenGlove—A Modular Wearable Device to Measure Kinematic Parameters of The Human Hand. Bioengineering 2023, 10, 324. https://doi.org/10.3390/bioengineering10030324
David JP, Helbig T, Witte H. SenGlove—A Modular Wearable Device to Measure Kinematic Parameters of The Human Hand. Bioengineering. 2023; 10(3):324. https://doi.org/10.3390/bioengineering10030324
Chicago/Turabian StyleDavid, Jonas Paul, Thomas Helbig, and Hartmut Witte. 2023. "SenGlove—A Modular Wearable Device to Measure Kinematic Parameters of The Human Hand" Bioengineering 10, no. 3: 324. https://doi.org/10.3390/bioengineering10030324
APA StyleDavid, J. P., Helbig, T., & Witte, H. (2023). SenGlove—A Modular Wearable Device to Measure Kinematic Parameters of The Human Hand. Bioengineering, 10(3), 324. https://doi.org/10.3390/bioengineering10030324