Wind Turbine Wake Modeling in Accelerating Wind Field: A Preliminary Study on a Two-Dimensional Hill
Abstract
:1. Introduction
2. Formulation of the Wake Model
2.1. Thrust Coefficient
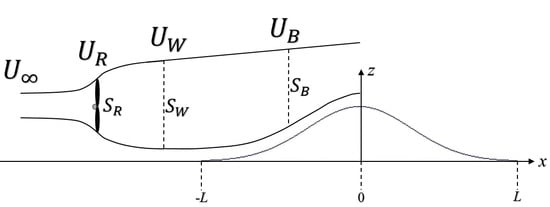
2.2. Wake Development over a Two-Dimensional Hill
3. Wind-Tunnel Testing
3.1. Test Facility
3.2. Test Model
3.2.1. Wind Turbine Model
3.2.2. Terrain Model
3.3. Measurement
3.4. Test Conditions
3.5. Measurement Results
3.5.1. Wind Speed Profiles over the Two-Dimensional Hill
3.5.2. Power and Thrust Coefficients over Flat Terrain
3.5.3. Wake over the Two-Dimensional Hill
3.5.4. Wake Development over Hill Versus Flat Terrain
4. Comparison between Wake Model and Wind-Tunnel Test
4.1. Thrust Coefficient
4.2. Wake Development
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | Slope of the hill |
| Thrust coefficient | |
| Thrust coefficient calculated by the wake wind speed profiles over the two-dimensional hill | |
| Power coefficient | |
| D | Wind turbine rotor diameter |
| Wake Width | |
| h | Height of the two-dimensional hill (same as the hub height) |
| L | Two-dimensional hill half-length |
| Momentum loss in the wake caused by the rotor | |
| Rate of change of momentum caused by the terrain | |
| R | Wind turbine rotor radius |
| S | Cross sectional area of the wind stream tube |
| Thrust | |
| Wind velocity | |
| Wind velocity outside the wake at location B | |
| λ | Tip speed ratio |
| ρ | Density |
| Rotor speed in rad/s | |
| Subscript | |
| R | Relevant to circumstances at the rotor |
| W | Relevant to circumstances in the wake (between the rotor and x = −L) |
| B | Relevant to circumstances between x = −L and x = 0 |
| Relevant to circumstances upstream of the turbine | |
| Acronyms | |
| ABL | Atmospheric Boundary Layer |
| AD | Actuator Disc |
| AL | Actuator Line |
| CFD | Computational Fluid Dynamics |
| HAWT | Horizontal Axis Wind Turbine |
| LES | Large Eddy Simulation |
References
- Cleijne, J.W. Results of Sexbierum Wind Farm: Single Wake Measurements; TNO-Report 93-082; TNO Institute of Environmental and Energy Technology: Apeldoorn, The Netherlands, 1993. [Google Scholar]
- Lissaman, P.B.S. Energy Effectiveness of Arbitrary Arrays of Wind Turbines. J. Energy 1979, 3, 323–328. [Google Scholar] [CrossRef]
- Neustadter, H.E.; Spera, D.A. Method for Evaluating Wind Turbine Wake Effects on Wind Farm Performance. J. Sol. Energy Eng. 1985, 107, 240–243. [Google Scholar] [CrossRef]
- Barthelmie, R.J.; Frandsen, S.T.; Hansen, K.; Schepers, J.G.; Rados, K.; Schlez, W.; Neubert, A.; Jensen, L.E.; Neckelmann, S. Modelling the impact of wakes on power output at Nysted and Horns Rev. In Proceedings of the European Wind Energy Conference and Exhibition, Marseilles, France, 16–19 March 2009. [Google Scholar]
- Barthelmie, R.J.; Frandsen, S.T.; Rathmann, O.; Politis, E.S.; Prospathopoulos, J.; Rados, K.; Hansen, K.; Cabezon, D.; Schlez, W.; Phillips, J.; et al. Flow and wakes in large wind farms in complex terrain and offshore. In Proceedings of the American Wind Energy Association Conference, Houston, TX, USA, 1–4 June 2008. [Google Scholar]
- Ibrahim, O.M.A.M.; Yoshida, S. Experimental and Numerical Studies of a Horizontal Axis Wind Turbine Performance over a Steep 2D Hill. Evergreen 2018, 5, 12–21. [Google Scholar] [CrossRef]
- Yoshida, S. Performance of Downwind Turbines in Complex Terrains. Wind Eng. 2006, 30, 487–501. [Google Scholar] [CrossRef]
- Ibrahim, O.M.A.M.; Yoshida, S.; Hamasaki, M.; Takada, A. Decay Factor of Wind Turbine Wake in Accelerated Wind Field. In Proceedings of the JWEA Wind Energy Symposium, Tokyo, Japan, 4–5 December 2018. [Google Scholar]
- Uchida, T.; Maruyama, T.; Ishikawa, H.; Zako, M.; Deguchi, A. Investigation of the Causes of Wind Turbine Blade Damage at Shiratakiyama Wind Farm in Japan: A Computer Simulation Based Approach; Reports; Research Institute for Applied Mechanics, Kyushu University: Fukuoka, Japan, 2011; pp. 13–25. [Google Scholar]
- Li, G.; Takakuwa, S.; Uchida, T. Application of CFD for Turbulence Related Operational Risks Assessment of Wind Turbines in Complex Terrain. In Proceedings of the EWEA2013 Conference Proceedings, Vienna, Austria, 4–7 February 2013. [Google Scholar]
- Tian, W.; Ozbay, A.; Yuan, W.; Sarakar, P.; Hu, H. An Experimental Study on the Performances of Wind Turbines Over Complex Terrain. In Proceedings of the 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar] [CrossRef]
- Webster, D.R.; DeGraaff, D.B.; Eaton, J.K. Turbulence Characteristics of a Boundary Layer Over a Two-Dimensional Bump. J. Fluid Mech. 1996, 320, 53–69. [Google Scholar] [CrossRef]
- Helmis, C.G.; Papadopoulos, K.H.; Asimakopoulos, D.N.; Papageorgas, P.G.; Soilemes, A.T. An Experimental Study of the Near-Wake Structure of a Wind Turbine Operating Over Complex Terrain. Sol. Energy 1995, 54, 413–428. [Google Scholar] [CrossRef]
- Ayotte, K.W.; Hughes, D.E. Observations of Boundary-Layer Wind-Tunnel Flow Over Isolated Ridges of Varying Steepness and Roughness. Bound. Layer Meteorol. 2004, 112, 525–556. [Google Scholar] [CrossRef]
- Walmsley, J.L.; Taylor, P.A.; Keith, T. A simple model of neutrally stratified boundary-layer flow over complex terrain with surface roughness modulations (MS3DJH/3R). Bound. Layer Meteorol. 1986, 36, 157–186. [Google Scholar] [CrossRef]
- Beljaars, A.C.M.; Walmsley, J.L.; Taylor, P.A. A mixed spectral finite-difference model for neutrally stratified boundary-layer flow over roughness changes and topography. Bound. Layer Meteorol. 1987, 38, 273–303. [Google Scholar] [CrossRef]
- Troen, I.; Petersen, E.L. European Wind Atlas; Risø National Laboratory: Roskilde, Denmark, 1989; p. 656. [Google Scholar]
- Ayotte, K.W.; Taylor, P.A. A Mixed Spectral Finite-Difference 3D Model of Neutral Planetary Boundary-Layer Flow over Topography. J. Atmos. Sci. 1995, 52, 3523–3538. [Google Scholar] [CrossRef] [Green Version]
- Cao, S.; Tamura, T. Experimental study on roughness effects on turbulent boundary layer flow over a two-dimensional steep hill. J. Wind Eng. Ind. Aerodyn. 2006, 94, 1–19. [Google Scholar] [CrossRef]
- Allen, T. Flow over Hills with Variable Roughness. Bound. Layer Meteorol. 2006, 121, 475–490. [Google Scholar] [CrossRef]
- Cao, S.; Tamura, T. Effects of roughness blocks on atmospheric boundary layer flow over a two-dimensional low hill with/without sudden roughness change. J. Wind Eng. Ind. Aerodyn. 2007, 95, 679–695. [Google Scholar] [CrossRef]
- Politis, E.S.; Prospathopoulos, J.; Cabezon, D.; Hansen, K.S.; Chaviaropoulos, P.K.; Barthelmie, R.J. Modeling wake effects in large wind farms in complex terrain: The problem, the methods and the issues. Wind Energy 2012, 15, 161–182. [Google Scholar] [CrossRef]
- Makridis, A.; Chick, J. Validation of a CFD model of wind turbine wakes with terrain effects. J. Wind Eng. Ind. Aerodyn. 2013, 123, 12–29. [Google Scholar] [CrossRef]
- Hansen, K.S.; Larsen, G.C.; Menke, R.; Vasiljevic, N.; Angelou, N.; Feng, J.; Zhu, W.J.; Vignaroli, A.; Xu, C.; Shen, W.Z. Wind turbine wake measurement in complex terrain. J. Phys. Conf. Ser. 2016, 753, 032013. [Google Scholar] [CrossRef] [Green Version]
- Castellani, F.; Astolfi, D.; Mana, M.; Piccioni, E.; Becchetti, M.; Terzi, L. Investigation of terrain and wake effects on the performance of wind farms in complex terrain using numerical and experimental data. Wind Energy 2017, 20, 1277–1289. [Google Scholar]
- Astolfi, D.; Castellani, F.; Terzi, L. A study of wind turbine wakes in complex terrain through RANS simulation and SCADA data. J. Sol. Energy Eng. 2018, 140, 031001. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Segalini, A. Qualitative analysis of wind-turbine wakes over hilly terrain. J. Phys. Conf. Ser. 2017, 854, 012023. [Google Scholar] [CrossRef] [Green Version]
- Hyvärinen, A.; Segalini, A. Effects from complex terrain on wind-turbine performance. J. Energy Resour. Technol. 2017, 139, 051205. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Lu, H.; Conzemius, R.J. Large-Eddy Simulation of Atmospheric Boundary Layer Flow through Wind Turbines and Wind Farms. J. Wind Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Zhong, H.; Du, P.; Tang, F.; Wang, L. Lagrangian Dynamic Large-Eddy Simulation of Wind Turbine near Wakes Combined with an Actuator Line Method. Appl. Energy 2015, 144, 224–233. [Google Scholar] [CrossRef]
- Berg, J.; Troldborg, N.; Sørensen, N.N.; Patton, E.G.; Sullivan, P.P. Large-Eddy Simulation of Turbine Wake in Complex Terrain. J. Phys. Conf. Ser. 2017, 854, 012003. [Google Scholar] [CrossRef]
- Tabib, M.; Rasheed, A.; Fuchs, F. Analyzing complex wake-terrain interactions and its implications on wind-farm performance. J. Phys. Conf. Ser. 2016, 753, 032063. [Google Scholar] [CrossRef]
- Vermeer, L.J.; Sørensen, J.N.; Crespo, A. Wind Turbine Wake Aerodynamics. Prog. Aerosp. Sci. 2003, 39, 467–510. [Google Scholar] [CrossRef]
- Sanderse, B. Aerodynamics of Wind Turbine Wakes—Literature Review; Report ECN-E–09-016; Energy research Centre of the Netherlands: Petten, The Netherlands, 2009. [Google Scholar]
- Katic, I.; Højstrup, J.; Jensen, N.O. A simple model for cluster efficiency. In Proceedings of the European Wind Energy Association Conference and Exhibition, Rome, Italy, 7–9 October 1986. [Google Scholar]
- Feng, J.; Shen, W.Z. Wind farm layout optimization in complex terrain: A preliminary study on a Gaussian hill. J. Phys. Conf. Ser. 2014, 524, 012146. [Google Scholar] [CrossRef]
- Research Institute for Applied Mechanics (RIAM), Kyushu University. Wind Engineering Section. Available online: http://www.riam.kyushu-u.ac.jp/windeng/en_index.html (accessed on 6 June 2019).
- Ohya, Y.; Karasudani, T. A shrouded wind turbine generating high output power with wind-lens technology. Energies 2010, 3, 634–649. [Google Scholar] [CrossRef]
- Goltenbott, U.; Ohya, Y.; Yoshida, S.; Jamieson, P. Aerodynamic interaction of diffuser augmented wind turbines in multi-rotor systems. Renew. Energy 2017, 112, 25–34. [Google Scholar] [CrossRef]
- Nissho Electric Works Co., Ltd. Available online: http://www.nissho-ew.co.jp/_userdata/LMC-6566A.pdf (accessed on 7 June 2019).














| Location Number | x [mm] | x/L | Distance from Location 1 |
|---|---|---|---|
| 1 | −1560 | −1 | 0 |
| 2 | −1170 | −3/4 | 0.76 D |
| 3 | −780 | −1/2 | 1.52 D |
| 4 | −390 | −1/4 | 2.29 D |
| 5 | 0 | 0 | 3.05 D |
| 6 | 390 | 1/4 | 3.81 D |
| 7 | 780 | 1/2 | 4.57 D |
| 8 | 1170 | 3/4 | 5.33 D |
| 9 | 1560 | 1 | 6.09 D |
| Model Number | LMC-6566A-50N | |
|---|---|---|
| Capacity | 50 N | 5 N m |
| 50 N | 5 N m | |
| 100 N | 5 N m | |
| rpm | Tip Speed Ratio (λ) |
|---|---|
| 261 | 1.0 |
| 392 | 1.5 |
| 522 | 2.0 |
| 653 | 2.5 |
| 783 | 3.0 |
| 914 | 3.5 |
| 1044 | 4.0 |
| 1175 | 4.5 |
| 1306 | 5.0 |
| 1436 | 5.5 |
| 1567 | 6.0 |
| Parameters | Flat Terrain | x/L = −1/2 | x/L = −1/4 | x/L = 0 |
|---|---|---|---|---|
| 2.20 | 2.02 | 1.73 | 0.59 | |
| 1.07 | 1.15 | 1.30 | 1.39 | |
| 0.64 | 0.85 | 0.99 | 1.19 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ibrahim, O.M.A.M.; Yoshida, S.; Hamasaki, M.; Takada, A. Wind Turbine Wake Modeling in Accelerating Wind Field: A Preliminary Study on a Two-Dimensional Hill. Fluids 2019, 4, 153. https://doi.org/10.3390/fluids4030153
Ibrahim OMAM, Yoshida S, Hamasaki M, Takada A. Wind Turbine Wake Modeling in Accelerating Wind Field: A Preliminary Study on a Two-Dimensional Hill. Fluids. 2019; 4(3):153. https://doi.org/10.3390/fluids4030153
Chicago/Turabian StyleIbrahim, Omar M. A. M., Shigeo Yoshida, Masahiro Hamasaki, and Ao Takada. 2019. "Wind Turbine Wake Modeling in Accelerating Wind Field: A Preliminary Study on a Two-Dimensional Hill" Fluids 4, no. 3: 153. https://doi.org/10.3390/fluids4030153
APA StyleIbrahim, O. M. A. M., Yoshida, S., Hamasaki, M., & Takada, A. (2019). Wind Turbine Wake Modeling in Accelerating Wind Field: A Preliminary Study on a Two-Dimensional Hill. Fluids, 4(3), 153. https://doi.org/10.3390/fluids4030153