Density, Viscosity and Free Energy of Activation for Viscous Flow of Monoethanol Amine (1) + H2O (2) + CO2 (3) Mixtures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation and CO2 Loading Analysis
2.2. Density Measurements
2.3. Viscosity Measurements
3. Experimental Uncertainty
4. Results and Discussion
4.1. Density of MEA (1) + H2O (2) + CO2 (3) Mixtures
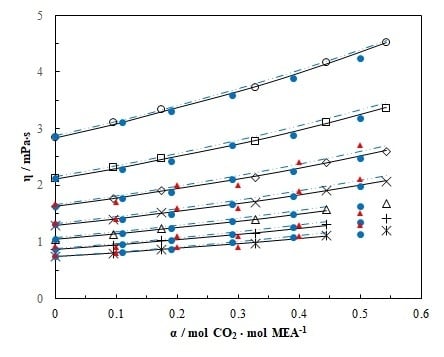
4.2. Viscosity of MEA (1) + H2O (2) + CO2 (3) Mixtures
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Han, J.; Jin, J.; Eimer, D.A.; Melaaen, M.C. Density of water (1) + Monoethanolamine (2) + CO2 (3) from (298.15 to 413.15) K and surface tension of water (1) + Monoethanolamine (2) from (303.15 to 333.15) K. J. Chem. Eng. Data 2012, 57, 1095–1103. [Google Scholar] [CrossRef]
- Nwaoha, C.; Saiwan, C.; Supap, T.; Idem, R.; Tontiwachwuthikul, P.; Rongwong, W.; Al-Marri, M.J.; Benamor, A. Carbon dioxide (CO2) capture performance of aqueoustri-solvent blends containing 2-amino-2-methyl-1-propanol (AMP) and methyldiethanolamine (MDEA) promoted by diethylenetriamine (DETA). Int. J. Greenh. Gas Control 2016, 53, 292–304. [Google Scholar] [CrossRef]
- Kidnay, A.J.; Parrish, W.R. Fundamentals of Natural Gas Processing; Taylor & Francis Group: Boca Raton, FL, USA, 2006. [Google Scholar]
- Maham, Y.; Teng, T.T.; Hepler, L.G.; Mather, A.E. Densities, excess molar volumes, and partial molar volumes for binary mixtures of Water with Monoethanolamine, Diethnolamine, and Triethanolamine from 25 to 80 °C. J. Solut. Chem. 1994, 23, 195–205. [Google Scholar] [CrossRef]
- Yang, F.; Wang, X.; Wang, W.; Liu, Z. Densities and excess properties of primary amines in alcoholic solutions. J. Chem. Eng. Data 2013, 58, 785–791. [Google Scholar] [CrossRef]
- Amundsen, T.G.; Øi, L.E.; Eimer, D.A. Density and viscosity of monoethanolamine + water + carbon dioxide from (25 to 80) °C. J. Chem. Eng. Data 2009, 54, 3096–3100. [Google Scholar] [CrossRef]
- Jayarathna, S.A.; Jayarathna, C.K.; Kottage, D.A.; Dayarathna, S.; Eimer, D.A.; Melaaen, M.C. Density and surface tension measurement of partially carbonated aqueous monoethanolamine solutions. J. Chem. Eng. Data 2013, 58, 343–348. [Google Scholar] [CrossRef]
- Jayarathna, S.; Weerasooriya, A.; Dayarathna, S.; Eimer, D.A.; Melaaen, M.C. Densities and surface tensions of CO2 loaded aqueous monoethanolamine solution with r = (0.2 to 0.7) at T = (303.15 to 333.15) K. J. Chem. Eng. Data 2013, 58, 986–992. [Google Scholar] [CrossRef]
- Weiland, R.H.; Dingman, J.C.; Cronin, D.B.; Browning, G.J. Density and viscosity of some partially carbonated aqueous alkanolamine solutions and their blends. J. Chem. Eng. Data 1998, 43, 378–382. [Google Scholar] [CrossRef]
- Hartono, A.; Mba, E.O.; Svendsen, H.F. Physical properties of partially CO2 loaded aqueous monoethanolamine (MEA). J. Chem. Eng. Data 2014, 59, 1808–1816. [Google Scholar] [CrossRef]
- Arachchige, U.S.P.R.; Aryal, N.; Eimer, D.A.; Melaaen, M.C. Viscosities of pure and aqueous solutions of Monoethanolamine (MEA), Diethanolamine (DEA), and N-Methyldiethanolamine (MDEA). In Proceedings of the Annual Transactions of the Nordic Rheology Society, Copenhagen, Demark, 12–14 June 2013. [Google Scholar]
- Hsu, C.-H.; Li, M.-H. Viscosities of Aqueous Blended Amines. J. Chem. Eng. Data 1997, 42, 714–720. [Google Scholar] [CrossRef]
- Versteeg, G.F.; Van Swaaij, W.P.M. Solubility and diffusivity of acid gases (carbon dioxide, nitrous oxide) in aqueous alkanolamine solutions. J. Chem. Eng. Data 1988, 33, 29–34. [Google Scholar] [CrossRef] [Green Version]
- Aronu, U.E.; Hartono, A.; Svendsen, H.F. Density, viscosity, and N2O solubility of aqueous amino acid salt and amine amino acid salt solutions. J. Chem. Thermodyn. 2012, 45, 90–99. [Google Scholar] [CrossRef]
- McAllister, R.A. The viscosity of liquid mixtures. AIChE. J. 1960, 6, 427–431. [Google Scholar] [CrossRef]
- Redlich, O.; Kister, A.T. Algebraic representation of thermodynamic properties and the classification of solutions. Ind. Eng. Chem. 1948, 40, 345–348. [Google Scholar] [CrossRef]
- Islam, M.N.; Islam, M.M.; Yeasmin, M.N. Viscosity of aqueous solution of 2-methoxyethanol, 2-ethoxyethanol, and ethanolamine. J. Chem. Thermodyn. 2004, 36, 889–893. [Google Scholar] [CrossRef]
- Eyring, H. Viscosity, Plasticity, and Diffusion as example of absolute reaction rates. J. Chem. Phys. 1936, 4, 283–291. [Google Scholar] [CrossRef]
- JCGM. Evaluation of measurement data—Supplement 1 to the Guide to the Expression of Uncertainty In Measurement—Propagation of Distributions Using a Monte Carlo Method. In JCGM 101: 2008; JCGM: Sevres, France, 2008. [Google Scholar]
- Ellison, S.L.R.; Williams, A. Eurachem/CITAC Guide: Quantifying Uncertainty in Analytical Measurement, 3rd ed.; 2012; Available online: http://www.eurachem.org (accessed on 15 November 2019).
- Nhaesi, A.H. A Study of the Predictive Models for the Viscosity of Multi-Component Liquid Regular Solutions. Ph.D. Thesis, University of Windsor, Windsor, UK, 1998. Available online: https://core.ac.uk/download/pdf/72774384.pdf (accessed on 15 November 2019).
- Macías-Salinas, R.; Aquino-Olivos, M.A.; García-Sánchez, F. Viscosity modelling of reservoir fluids over wide temperature and pressure ranges. Chem. Eng. Trans. 2013, 32, 1573–1578. [Google Scholar] [CrossRef]
- Korson, L.; Hansen, W.D.; Millero, F.J. Viscosity of water at various temperatures. J. Phys. Chem. 1969, 73, 34–39. [Google Scholar] [CrossRef]
- Kestin, J.; Sokolov, M.; Wakeham, W.A. Viscosity of liquid water in the range −8 °C to 150 °C. J. Phys. Chem. Ref. Data 1978, 7, 941–948. [Google Scholar] [CrossRef] [Green Version]
- Karunarathne, S.S.; Eimer, D.A.; Øi, L.E. Evaluation of systematic error and uncertainty of viscosity measurements of mixtures of monoethanol amine and water in coaxial cylinder rheometers. Int. J. Model. Optim. 2018, 8, 260–265. [Google Scholar] [CrossRef]
- Idris, Z.; Kummamuru, N.B.; Eimer, D.A. Viscosity measurement of unloaded and CO2-loaded aqueous monoethanolamine at higher concentrations. J. Mol. Liq. 2017, 243, 638–645. [Google Scholar] [CrossRef]
- Hartono, A.; Svendsen, H.F. Density, viscosity, and excess properties of aqueous solution of diethylenetriamine (DETA). J. Chem. Thermodyn. 2009, 41, 973–979. [Google Scholar] [CrossRef]
- Maham, Y.; Liew, C.N.; Mather, A.E. Viscosities and Excess Properties of Aqueous Solutions of Ethanolamines from 25 to 80 °C. J. Solut. Chem. 2002, 31, 743–756. [Google Scholar] [CrossRef]
- Heric, E.L.; Brewer, J.G. Viscosity of some binary liquid nonelectrolyte mixtures. J. Chem. Eng. Data 1967, 12, 574–583. [Google Scholar] [CrossRef]
- Mahajan, A.R.; Mirgane, S.R. Excess molar volumes and viscosities for the binary mixtures of n-Octane, n-Decane, n-Dodecane, and n-Tetradecane with Octan-2-ol at 298.15 K. J. Thermodyn. 2013, 2013, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Idris, Z.; Kummamuru, N.B.; Eimer, D.A. Viscosity measurement and correlation of unloaded and CO2 loaded 3-Amino-1-propanol solution. J. Chem. Eng. Data 2018, 63, 1454–1459. [Google Scholar] [CrossRef]
- Stec, M.; Spietz, T.; Wieclaw-Solny, L.; Tatarczuk, A.; Wilk, A.; Sobolewski, A. Density of unloaded and CO2-loaded aqueous solutions of piperazine and 2-amino-2-methyl-1-propanol and their mixtures from 293.15 to 333.15 K. Phys. Chem. Liq. 2015, 54, 475–486. [Google Scholar] [CrossRef]
- Matin, N.S.; Remias, J.E.; Liu, K. Application of electrolyte-NRTL model for prediction of the viscosity of carbon dioxide loaded aqueous amine solutions Ind. Eng. Chem. Res 2013, 52, 16979–16984. [Google Scholar] [CrossRef]
- Perticaroli, S.; Mostofian, B.; Ehlers, G.; Neuefeind, J.C.; Diallo, S.O.; Stanley, C.B.; Daemen, L.; Egami, T.; Katsaras, J.; Cheng, X.; et al. Structural relaxation, viscosity, and network connectivity in a hydrogen bonding liquid. Phys. Chem. Chem. Phys. 2017, 19, 25859–25869. [Google Scholar] [CrossRef]










| Chemical Name | CAS Reg. No. | Mole Fraction Purity a | Source | Purification |
|---|---|---|---|---|
| monoethanol amine (MEA) | 141-43-5 | ≥0.995 (GC b) | Sigma–Aldrich | no |
| carbon dioxide (CO2) | 124-38-9 | 0.99999 | AGA Norge AS | no |
| nitrogen (N2) | 7727-37-9 | 0.99999 | AGA Norge AS | no |
| sodium hydroxide (NaOH) | 1310-73-2 | - | Merck KGaA | no |
| hydrochloric acid (HCl) | 7647-01-0 | - | Merck KGaA | no |
| barium chloride dihydrate (BaCl2·2H2O) | 10326-27-9 | ≥0.99 | Merck KGaA | no |
| T/K | No. Points | Parameters | |
|---|---|---|---|
| 0.3–0.9 | 293.15–363.15 | 56 | = 683.5 |
| = 1.344 × 105 | |||
| = −1.089 × 104 | |||
| = 145.2 | |||
| = 567.9 | |||
| AARD (%) | 0.12 | ||
| AMD (kg·m−3) | 3.45 | ||
| Measured Density ρ/kg·m−3 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 293.15 K | 303.15 K | 313.15 K | 323.15 K | 333.15 K | 343.15 K | 353.15 K | 363.15 K | ||
| 0.3 | 0.1122 | 1012.6 1012.68 d | 1008.2 1008.4 b 1008.31 d 1008.2 e | 1003.3 1003.3 b 1003.4 c 1003.45 d 1003.3 e | 997.9 998.1 b 998.1 c 998.07 d 998.1 e | 991.6 992.3 b 992.23 d 992.3 e | 986.0 986.1 b 985.8 c 985.96 d | 979.4 979.4 b 979.4 c 979.27 d | 972.3 972.5 b |
| 0.4 | 0.1643 | 1018.4 | 1013.3 1013.8 b 1013.3 e | 1007.8 1008.3 b 1007.7 c 1007.8 e | 1001.8 1002.3 b 1001.8 c 1002.1 e | 995.5 996.1 b 995.7 e | 988.9 989.4 b 988.9 c | 981.9 982.4 b 981.9 c | 974.6 975.0 b |
| 0.5 | 0.2278 | 1023.6 | 1017.8 1018.2 b 1017.8 e | 1011.6 1012.1 b 1011.7 c 1011.8 e | 1005.2 1005.6 b 1005.3 c 1005.4 e | 998.4 999.0 b 998.7 e | 991.4 991.9 b 991.5 c | 984.1 984.5 b 984.2 c | 976.4 976.9 b |
| 0.6 | 0.3067 | 1027.7 | 1021.2 1021.4 b 1021.3 e | 1014.5 1014.7 b 1014.6 e | 1007.6 1007.8 b 1007.8 e | 1000.4 1000.7 b 1000.6 e | 993.0 993.2 b | 985.4 985.6 b | 977.4 977.7 b |
| 0.7 | 0.4077 | 1029.3 | 1022.4 1022.8 b 1022.6 e | 1015.2 1015.7 b 1015.5 c 1015.5 e | 1007.9 1008.3 b 1008.2 c 1008.2 e | 1000.4 1000.8 b 1000.6 e | 992.7 993.1 b 993.0 c | 984.8 985.2 b 985.0 c | 976.4 977.1 b |
| 0.8 | 0.5412 | 1028.1 | 1020.8 1021.0 b | 1013.3 1013.5 b | 1005.7 1005.9 b | 997.9 998.2 b | 990.0 990.2 b | 981.9 982.1 b | 973.6 973.9 b |
| 0.9 | 0.7264 | 1023.5 | 1015.8 1016.2 b | 1008.1 1008.5 b 1008.4 c | 1000.3 1000.6 b 1000.6 c | 992.4 992.7 b | 984.3 984.6 b 984.6 c | 976.1 976.5 b 976.4 c | 967.8 968.1 b |
| 1 | 1.0000 | 1015.9 | 1008.1 1008.0 b | 1000.1 1000.0 b 1000.3 c | 992.1 992.0 b 992.3 c | 984.0 983.9 b | 975.9 975.8 b 976.0 c | 967.6 967.5 b 967.8 c | 959.3 959.2 b |
| 293.15 K | 303.15 K | 313.15 K | 323.15 K | 333.15 K | 343.15 K | 353.15 K | ||
|---|---|---|---|---|---|---|---|---|
| 0.0000 | 0.000 | 1012.6 | 1008.2 | 1003.3 | 997.9 | 991.6 | 986.0 | 979.4 |
| 0.0105 | 0.095 | 1032.0 | 1027.6 | 1022.8 | 1017.4 | 1011.6 | 1005.1 | 995.5 |
| 0.0193 | 0.175 | 1052.5 | 1048.1 | 1043.3 | 1038.1 | 1032.4 | 1026.4 | 1020.1 |
| 0.0355 | 0.328 | 1077.8 | 1073.4 | 1068.6 | 1063.4 | 1057.9 | 1052.0 | 1044.1 |
| 0.0476 | 0.445 | 1103.3 | 1097.7 | 1092.8 | 1087.6 | 1082.1 | 1075.7 | 1069.3 |
| 0.0574 | 0.543 | 1123.1 | 1118.4 | 1113.4 | 1107.9 | |||
| 0.0000 | 0.000 | 1018.4 | 1013.3 | 1007.8 | 1001.9 | 995.5 | 988.9 | 981.9 |
| 0.0170 | 0.105 | 1045.6 | 1040.7 | 1035.3 | 1029.6 | 1023.6 | 1017.3 | 1010.6 |
| 0.0341 | 0.215 | 1073.4 | 1068.5 | 1063.3 | 1057.8 | 1051.9 | 1045.8 | 1039.4 |
| 0.0507 | 0.325 | 1102.0 | 1097.2 | 1092.0 | 1086.5 | 1080.8 | 1074.9 | 1068.6 |
| 0.0669 | 0.436 | 1130.3 | 1125.4 | 1120.2 | 1114.7 | 1109.2 | 1103.2 | 1097.0 |
| 0.0826 | 0.548 | 1155.5 | 1150.4 | 1145.1 | 1139.5 | |||
| 0.0000 | 0.000 | 1023.6 | 1017.8 | 1011.6 | 1005.2 | 998.4 | 991.4 | 984.1 |
| 0.0205 | 0.092 | 1052.3 | 1046.7 | 1040.9 | 1034.7 | 1028.3 | 1021.7 | 1014.8 |
| 0.0406 | 0.186 | 1082.4 | 1077.0 | 1071.4 | 1065.5 | 1059.4 | 1053.0 | 1046.4 |
| 0.0620 | 0.290 | 1112.7 | 1107.4 | 1101.9 | 1096.2 | 1090.3 | 1084.2 | 1077.9 |
| 0.0825 | 0.395 | 1144.5 | 1139.2 | 1133.8 | 1128.3 | 1122.5 | 1116.6 | 1110.5 |
| 0.1013 | 0.495 | 1175.7 | 1170.4 | 1165.0 | 1159.4 | 1153.6 | 1147.5 | |
| Parameters | |||
|---|---|---|---|
| 0.6802 | 0.7731 | 0.7506 | |
| 0.001951 | 0.001354 | 0.001494 | |
| −2.97 × 10−6 | −2.015 × 10−6 | −2.237 × 10−6 | |
| 2.346 | 2.164 | 2.015 | |
| AARD (%) | 0.15 | 0.08 | 0.15 |
| AMD (kg·m−3) | 4.2 | 2 | 3.8 |
| T/K | Parameters | |
|---|---|---|
| 0–1 | 298.15–363.15 | = 16.2 |
| = −0.03473 | ||
| = −4.853 | ||
| = 0.008315 | ||
| = −6.433 | ||
| = 0.02065 | ||
| R2 = 0.998 | ||
| /mPa·s | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 293.15 K | 303.15 K | 313.15 K | 323.15 K | 333.15 K | 343.15 K | 353.15 K | 363.15 K | ||
| 0.3 | 0.1122 | 2.836 2.874 b 2.879 b | 2.109 2.133 b 2.130 b | 1.628 1.628 b 1.638 b 1.67 c | 1.290 1.305 b 1.318 b 1.33 c | 1.046 1.055 b 1.067 b | 0.866 0.878 b 0.874 b 0.92 c | 0.740 0.742 b 0.740 b 0.77 c | 0.687 |
| 0.4 | 0.1643 | 4.285 | 3.080 | 2.305 2.28 c | 1.782 1.75 c | 1.417 | 1.154 1.14 c | 0.960 0.95 c | 0.808 |
| 0.5 | 0.2278 | 6.610 | 4.580 4.69 d | 3.310 3.39 c 3.37 d | 2.454 2.54 c 2.53 d | 1.915 1.94 d | 1.528 1.57 c 1.54 d | 1.243 1.28 c 1.26 d | 1.029 1.05 d |
| 0.6 | 0.3067 | 10.217 | 6.769 6.92 d | 4.736 4.77 d | 3.444 3.45 d | 2.602 2.62 d | 2.031 2.04 d | 1.620 1.62 d | 1.319 1.34 d |
| 0.7 | 0.4077 | 15.348 | 9.823 9.89 d | 6.664 6.96 c 6.69 d | 4.720 4.94 c 4.76 d | 3.461 3.49 d | 2.615 2.79 c 2.63 d | 2.029 2.18 c 2.04 d | 1.616 1.63 d |
| 0.8 | 0.5412 | 20.521 | 12.840 13.38 d | 8.534 8.82 d | 5.937 6.11 d | 4.295 4.41 d | 3.217 3.26 d | 2.483 2.49 d | 1.962 1.97 d |
| 0.9 | 0.7264 | 24.027 | 14.963 15.12 d | 9.879 10.20 c 9.95 d | 6.829 7.06 c 6.88 d | 4.936 4.94 d | 3.683 3.81 c 3.67 d | 2.832 2.93 c 2.82 d | 2.222 2.23 d |
| 1 | 1.0000 | 23.376 | 14.748 14.77 d | 10.108 9.61 c 9.84 d | 6.935 6.72 c 6.87 d | 5.067 4.98 d | 3.834 3.69 c 3.72 d | 2.974 2.85 c 2.85 d | 2.364 2.26 d |
| Source (s) | No. Parameters | AARD (%) | AMD (mPa·s) |
|---|---|---|---|
| This work | 6 | 1.4 | 0.79 |
| Hartono, et al. [10] | 4 | 2.4 | 0.66 |
| Arachchige, et al. [11] | 7 | 3.5 | 1.1 |
| Islam, et al. [17] | 4 | 5.1 | 0.59 |
| (η/mPa·s) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 293.15 K | 303.15 K | 313.15 K | 323.15 K | 333.15 K | 343.15 K | 353.15 K | ||
| 0.0000 | 0.000 | 2.836 | 2.109 | 1.628 | 1.290 | 1.046 | 0.866 | 0.740 |
| 0.0105 | 0.095 | 3.103 | 2.305 | 1.768 | 1.397 | 1.128 | 0.937 | 0.788 |
| 0.0193 | 0.175 | 3.338 | 2.476 | 1.910 | 1.511 | 1.228 | 1.021 | 0.865 |
| 0.0355 | 0.328 | 3.730 | 2.764 | 2.138 | 1.699 | 1.384 | 1.152 | 0.977 |
| 0.0476 | 0.445 | 4.164 | 3.105 | 2.403 | 1.913 | 1.562 | 1.308 | 1.118 |
| 0.0574 | 0.543 | 4.515 | 3.360 | 2.602 | 2.064 | 1.680 | 1.403 | 1.191 |
| 0.0000 | 0.000 | 4.285 | 3.080 | 2.305 | 1.782 | 1.417 | 1.154 | 0.960 |
| 0.0170 | 0.105 | 4.793 | 3.423 | 2.567 | 1.985 | 1.590 | 1.302 | 1.090 |
| 0.0341 | 0.215 | 5.524 | 3.944 | 2.968 | 2.308 | 1.851 | 1.526 | 1.286 |
| 0.0507 | 0.325 | 6.496 | 4.655 | 3.502 | 2.726 | 2.198 | 1.813 | 1.524 |
| 0.0669 | 0.436 | 7.639 | 5.442 | 4.084 | 3.177 | 2.556 | 2.111 | 1.781 |
| 0.0826 | 0.548 | 8.820 | 6.203 | 4.614 | 3.544 | 2.821 | 2.302 | 1.917 |
| 0.0000 | 0.000 | 6.610 | 4.580 | 3.310 | 2.454 | 1.915 | 1.528 | 1.243 |
| 0.0205 | 0.092 | 7.859 | 5.378 | 3.926 | 2.955 | 2.303 | 1.838 | 1.493 |
| 0.0406 | 0.186 | 9.518 | 6.529 | 4.756 | 3.594 | 2.813 | 2.269 | 1.866 |
| 0.0620 | 0.290 | 11.611 | 7.904 | 5.710 | 4.291 | 3.328 | 2.667 | 2.190 |
| 0.0825 | 0.395 | 14.854 | 10.073 | 7.247 | 5.422 | 4.227 | 3.409 | 2.809 |
| 0.1013 | 0.495 | 19.348 | 12.841 | 9.068 | 6.678 | 5.169 | 4.118 | 3.365 |
| T/K | Parameters | w1 = 0.5 | ||
|---|---|---|---|---|
| 298.15–343.15 | d1 | 4.536 | 2.554 | 8.533 |
| 0.006765 | 0.01205 | −0.0037 | ||
| 12.08 | 19.46 | 17.79 | ||
| AARD (%) | 0.58 | 1.13 | 1.25 | |
| AMD (mPa·s) | 0.03 | 0.22 | 1.04 | |
| T/K | 293.15 | 303.15 | 313.15 | 323.15 | 333.15 | 343.15 | 353.15 | |
|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.0000 | 12.375 | 12.062 | 11.798 | 11.564 | 11.358 | 11.177 | 11.060 |
| 0.0105 | 12.571 | 12.262 | 11.988 | 11.753 | 11.539 | 11.376 | 11.222 | |
| 0.0193 | 12.721 | 12.413 | 12.159 | 11.931 | 11.740 | 11.583 | 11.451 | |
| 0.0355 | 12.970 | 12.667 | 12.428 | 12.220 | 12.044 | 11.900 | 11.783 | |
| 0.0476 | 13.210 | 12.931 | 12.702 | 12.507 | 12.347 | 12.228 | 12.150 | |
| 0.0574 | 13.382 | 13.105 | 12.883 | 12.685 | ||||
| 0.4 | 0.0000 | 13.595 | 13.240 | 12.936 | 12.674 | 12.448 | 12.255 | 12.094 |
| 0.0170 | 13.835 | 13.471 | 13.179 | 12.924 | 12.726 | 12.556 | 12.419 | |
| 0.0341 | 14.148 | 13.793 | 13.521 | 13.291 | 13.105 | 12.965 | 12.860 | |
| 0.0507 | 14.509 | 14.175 | 13.914 | 13.698 | 13.540 | 13.413 | 13.312 | |
| 0.0669 | 14.870 | 14.534 | 14.278 | 14.072 | 13.919 | 13.807 | 13.725 | |
| 0.0826 | 15.194 | 14.837 | 14.568 | 14.337 | ||||
| 0.5 | 0.0000 | 14.891 | 14.489 | 14.137 | 13.802 | 13.560 | 13.344 | 13.148 |
| 0.0205 | 15.275 | 14.853 | 14.538 | 14.255 | 14.022 | 13.819 | 13.631 | |
| 0.0406 | 15.701 | 15.299 | 14.992 | 14.733 | 14.526 | 14.366 | 14.230 | |
| 0.0620 | 16.147 | 15.741 | 15.426 | 15.165 | 14.945 | 14.779 | 14.648 | |
| 0.0825 | 16.707 | 16.309 | 16.002 | 15.747 | 15.559 | 15.427 | 15.325 | |
| 0.1013 | 17.311 | 16.879 | 16.543 | 16.262 | 16.069 | 15.918 | ||
| ΔH*/kJ·mol−1 | |||
|---|---|---|---|
| 0.3 | 0.0000 | 18.834 | 22.301 |
| 0.0105 | 19.150 | 22.696 | |
| 0.0193 | 18.902 | 21.360 | |
| 0.0355 | 18.716 | 19.895 | |
| 0.0476 | 18.400 | 18.003 | |
| 0.0574 | 20.173 | 23.234 | |
| 0.4 | 0.0000 | 20.897 | 25.215 |
| 0.0170 | 20.688 | 23.742 | |
| 0.0341 | 20.377 | 21.642 | |
| 0.0507 | 20.266 | 20.026 | |
| 0.0669 | 20.379 | 19.209 | |
| 0.0826 | 23.540 | 28.578 | |
| 0.5 | 0.0000 | 23391 | 29.339 |
| 0.0205 | 23147 | 27.247 | |
| 0.0406 | 22773 | 24.566 | |
| 0.0620 | 23389 | 25.142 | |
| 0.0825 | 23381 | 23.248 | |
| 0.1013 | 25441 | 28.114 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karunarathne, S.S.; Eimer, D.A.; Øi, L.E. Density, Viscosity and Free Energy of Activation for Viscous Flow of Monoethanol Amine (1) + H2O (2) + CO2 (3) Mixtures. Fluids 2020, 5, 13. https://doi.org/10.3390/fluids5010013
Karunarathne SS, Eimer DA, Øi LE. Density, Viscosity and Free Energy of Activation for Viscous Flow of Monoethanol Amine (1) + H2O (2) + CO2 (3) Mixtures. Fluids. 2020; 5(1):13. https://doi.org/10.3390/fluids5010013
Chicago/Turabian StyleKarunarathne, Sumudu S., Dag A. Eimer, and Lars E. Øi. 2020. "Density, Viscosity and Free Energy of Activation for Viscous Flow of Monoethanol Amine (1) + H2O (2) + CO2 (3) Mixtures" Fluids 5, no. 1: 13. https://doi.org/10.3390/fluids5010013
APA StyleKarunarathne, S. S., Eimer, D. A., & Øi, L. E. (2020). Density, Viscosity and Free Energy of Activation for Viscous Flow of Monoethanol Amine (1) + H2O (2) + CO2 (3) Mixtures. Fluids, 5(1), 13. https://doi.org/10.3390/fluids5010013