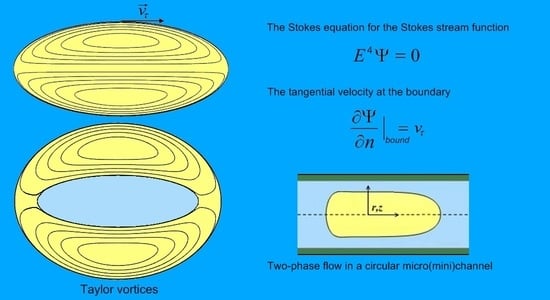
Mathematical Model for Axisymmetric Taylor Flows Inside a Drop

Abstract

Analytical solutions of the Stokes equations written as a differential equation for the Stokes stream function were obtained. These solutions describe three-dimensional axisymmetric flows of a viscous liquid inside a drop that has the shape of a spheroid of rotation and have a similar set of characteristics with Taylor flows inside bubbles that occur during the transfer of a two-component mixture through tubes.

1. Introduction

The Taylor flow regime is the most favorable of the known regimes for microchannels, since it provides, on the one hand, an intensification of mass transfer due to Taylor vortices, and on the other hand, a sufficient residence time, in view of the rather moderate velocities of phase motion (typically 0.01–0.1 m/s, and not larger than 0.8–1 m/s), which are typical for this regime [1,2]. The velocity of bubbles or droplets is characterized by capillary number Ca = μU/σ where μ is a liquid viscosity, U is adispersed phase (bubbles or droplets) velocity and σ is an interfacial tension. Usually Ca number does not exceed 0.01–0.1, and the Reynolds number for the flows in micro and mini-channels is less than 2000, corresponding thus to the laminar flow [3]. These features make it possible to achieve a high mixing intensity without significantly complicating the equipment and generate great interest in this type of flow.

In the last two to three decades, many papers were devoted to both the hydrodynamics of the Taylor flow and mass transfer in it [4,5,6,7,8,9,10]. Most of these works in fluid dynamics are based on experimental or numerical experiments. At the same time, it is important to search for independent theoretical methods that allow one to obtain a general a priori idea of the dispersed flow inside droplets or bubbles, including the shape of streamlines.

Such two-component liquid streams belong to the class of Taylor streams and are widely used in various industries [1,2].

One of the first models describing the motion of Taylor bubbles in channels was published by F. Bretherton [11]. The extended Bretherton model for Taylor bubbles at moderate capillary numbers was proposed by E. Klaseboer [12].

A number of works [13,14,15,16] were devoted to the study of Taylor flows. In [17], the method of micro Particle Image Velocimetry is used to study Taylor vortices inside an elongated bubble. In [18] the circulation patterns within the dispersed phase for regular Taylor two-phase flows were constructed using the FEATFLOW program.

It is worth noting that the actual shape of the Taylor bubbles may be far from the ideal geometric shape. Nevertheless, modeling, which considers the Taylor flow in a domain with an idealized form, is used in a number of studies [19]. In [20,21], the shape of the bubbles is approximated by a part of a cylinder with hemispherical caps or a prolate ellipsoid at ends.

In the type of flow that we are considering, a mixture of two liquids that have different viscosity coefficients is transferred through the channel and one liquid is distributed in the form of bubbles inside the other one (Figure 1). The liquid interacting with the channel walls moves along its axis and drives the gas bubbles or the droplets of the second liquid. At a constant two-phase velocity of a mixture of liquids through the channel, this flow can be considered stationary and axisymmetric (for the case when the capillary forces dominate over gravitational forces, i.e., for liquids similar to the water at the channel diameter smaller than ≈ 3 mm).

Due to the presence of friction force at the boundary of two fluids and friction between the fluid and the channel walls, a vortex flow occurs in the inner part of the bubbles during the movement of the mixture through the channel (Figure 2).

In our previous work [22], we obtained solutions for two-dimensional flows inside an elliptical region, which demonstrated the presence of both the main toroidal vortex (similar to that shown in Figure 2) and two satellite vortices. These solutions generally reflect the nature of the droplet/bubble flows in the Taylor two-phase flow.

The system of Stokes equations is often used in mathematical models to describe the flow of a liquid with a set of characteristics similar to the Taylor flows described above. It should be noted that in most problems, the system of Stokes equations can be solved only numerically, and analytical solutions of Stokes equations have been found only for a small class of problems with a specific regular boundary shape [23,24]. In the presence of curvilinear sections of the boundary in some problems, it turns out to be expedient to use the corresponding curvilinear coordinate system. In [25], solutions were found for a circular cavity in a polar coordinate system; in [26], solutions of the Stokes equations were obtained in an elliptic coordinate system for a region bounded by two confocal ellipses. Solutions of the Stokes equations for two-dimensional flows inside an elliptic region were considered in article [22]. A similar approach is used for three-dimensional flows in cases where the boundary has a spherical or cylindrical shape [27,28].

The purpose of this work is to obtain analytical solutions of the Stokes equations for a mathematical model that describes the three-dimensional Taylor flow inside an elongated bubble (Figure 2). In the considered simplification of the physical model, the bubble shape is specified as the surface of a spheroid (ellipsoid of revolution), and the fluid flow inside the bubble is assumed to be axisymmetric. Thus, in comparison with work [22], in this article we simulate the flow for three-dimensional shape of the bubble boundary. Another form of boundary geometry leads to the emergence of a more complex axisymmetric pressure field inside the bubble and becomes a more accurate approximation of the real physical model.

The obtained analytical solutions of the Stokes equations make it possible to qualitatively compare the flow pattern inside the bubbles with experimental data and the results of numerical modeling for Taylor flows, and can also be used as a benchmark to assess the quality of numerical algorithms [29,30].

2. Problem Formulation

We are considering a three-dimensional axisymmetric Stokes flow in the region bounded by a spheroid (Figure 3). We assume that the boundary of the spheroid is impenetrable and the shape of the spheroid does not change over time. The fluid flow inside the spheroid is caused by the motion of the boundary, in which the velocity of the points on the boundary is directed tangentially to the boundary of the spheroid. In this problem, we will assume that the velocity vector at the boundary of the spheroid lies in the plane passing through the axis of symmetry of the spheroid.

The described type of flow inside the spheroid has a similar set of characteristics with Taylor flows inside bubbles (Figure 2) and represents their simplified mathematical model.

Let us consider the derivation of solutions to the Stokes equations that describe fluid flows for a given system. We introduce a cylindrical coordinate system $(r,z,\phi )$ centered at a point that halves the segment lying between the foci of the spheroid (Figure 3). Since the flow is axisymmetric, we can write equations in two coordinates $(r,z)$. A cross section of a spheroid is shown in Figure 4. The axis $OZ$ divides the border of the ellipse into two parts, $S_1$ and $S_2$. We assume that the distribution that defines the velocity at the boundary of the spheroid has the same form on any half and an ellipse ($S_1$, $S_2$) in any plane passing through the axis $OZ$.

The condition specifying the tangential velocity at the boundary will be written as:

$$v_{\tau }{|}_{S_1}=v_{S_1},v_{\tau }{|}_{S_2}=v_{S_2}$$

(1)

The radial component of the velocity on the axis of symmetry of the spheroid equals to zero:

$$v_r{|}_{OZ}=0$$

(2)

In the process of describing the fluid flow and constructing the solution of the Stokes equations in this work, we will use the Stokes stream function (it is necessary to distinguish this function from the stream function used in hydrodynamics to describe two-dimensional flows). Velocity components are related to the Stokes stream function by the following relations [23]:

$$v_r=\frac{1}{r}\frac{\partial \Psi }{\partial z},v_z=-\frac{1}{r}\frac{\partial \Psi }{\partial r}.$$

Let us formulate the boundary conditions for the Stokes stream function. Equation (2) will be written in the form:

$$\Psi {|}_{AB}=0$$

(3)

The normal component of the velocity at the ellipse boundary is equals to zero, therefore:

$$\Psi {|}_{S_1,S_2}=0$$

(4)

The condition for the tangential velocity (1) at the boundary of the ellipse takes the form:

$$\frac{\partial \Psi }{\partial n}{|}_{S_1}=v_{S_1},\frac{\partial \Psi }{\partial n}{|}_{S_2}=v_{S_2}$$

(5)

Taking into account the specific shape of the domain boundary, the solution of Stokes equations in elliptic coordinates $({\xi }_1,{\xi }_2,\phi )$ was derived:

$$\begin{array}{l}r=d\sinh ({\xi }_1)\sin ({\xi }_2)\\ z=d\cosh ({\xi }_1)\cos ({\xi }_2)\end{array}$$

$d$—focal length.

The Lame coefficients in elliptic coordinates are:

$$h_1=h_2=h=\frac{1}{d\sqrt{{\cosh }^2({\xi }_1)-{\cos }^2({\xi }_2)}}.$$

The Stokes equation for the Stokes stream function are written as [31]:

$$E^4\Psi =0$$

(6)

where the operator $E^2$ has the form:

$$E^2=r{h}^2\left[\frac{\partial }{\partial {\xi }_1}(\frac{1}{r}\frac{\partial }{\partial {\xi }_1})+\frac{\partial }{\partial {\xi }_2}(\frac{1}{r}\frac{\partial }{\partial {\xi }_2})\right]$$

(7)

Taking into account relation between coordinates $r=d\sinh ({\xi }_1)\sin ({\xi }_2)$, we get:

$$E^2=\frac{1}{d^2(c{h}^2({\xi }_1)-{\cos }^2({\xi }_2))}\left[\frac{{\partial }^2}{\partial {\xi }_1^2}+\frac{{\partial }^2}{\partial {\xi }_2^2}-cth({\xi }_1)\frac{\partial }{\partial {\xi }_1}-ctg({\xi }_2)\frac{\partial }{\partial {\xi }_2}\right]$$

(8)

It should be noted that Equation (6) differs from the classical biharmonic equation for the two-dimensional stream function [26]: Formula (8) includes the last two terms containing the hyperbolic cotangent and the cotangent, which are absent in the formula for the Laplace operator in elliptic coordinates.

In elliptical coordinates, the halves of the ellipse (Figure 4) will transform into two rectangles, given by the inequalities: $0\le {\xi }_1\le {\xi }_0$, $0\le {\xi }_2\le \pi$ and $0\le {\xi }_1\le {\xi }_0$, $\pi \le {\xi }_2\le 2\pi$ (Figure 5). The segment between the foci will correspond to the segments ${\xi }_1=0$, $0\le {\xi }_2\le \pi$, $\pi \le {\xi }_2\le 2\pi$. Parts of boundary $S_1$, $S_2$ will transform to segments ${\xi }_1={\xi }_0$, $0\le {\xi }_2\le \pi$, $\pi \le {\xi }_2\le 2\pi$. The segments between the foci and points $A$, $B$ will be segments ${\xi }_2=\pi$, ${\xi }_2=0$, $0\le {\xi }_1\le {\xi }_0$.

Let us formulate the boundary conditions for the Stokes stream function in elliptic coordinates. Condition (4) will be written as:

$$\Psi ({\xi }_0,{\xi }_2)=0,0\le {\xi }_2\le 2\pi$$

(9)

Condition (3) takes the form:

$$\Psi ({\xi }_1,0)=0,\Psi ({\xi }_1,\pi )=0,\Psi ({\xi }_1,2\pi )=0,\mathrm{for}0\le {\xi }_1\le {\xi }_0$$

(10)

$$\Psi (0,{\xi }_2)=0,\mathrm{for}0\le {\xi }_2\le 2\pi$$

(11)

We write the boundary condition for the tangential velocity (5) on the right half of the ellipse in the form:

$$\frac{1}{d\sqrt{{\cosh }^2({\xi }_1)-{\cos }^2({\xi }_2)}}\frac{\partial \Psi }{\partial {\xi }_1}({\xi }_1,{\xi }_2){|}_{{\xi }_1={\xi }_0}=V({\xi }_2),0\le {\xi }_2\le \pi$$

(12)

Further, we assume that the velocity at the boundary of the ellipse is symmetric about the axis $OZ$.

3. Problem Solution

In the process of constructing a solution of Equation (6), we perform the following replacement:

$$\begin{array}{l}\lambda =\cosh ({\xi }_1)\\ \eta =\cos ({\xi }_2)\end{array}$$

This replacement makes it possible to significantly simplify Formula (8) for the differential operator:

$$E^2=\frac{1}{d^2({\lambda }^2-{\eta }^2)}(({\lambda }^2-1)\frac{{\partial }^2}{\partial {\lambda }^2}+(1-{\eta }^2)\frac{{\partial }^2}{\partial {\eta }^2})$$

(13)

We will seek a solution in the form:

$$\Psi (\lambda ,\eta )=(1-{\eta }^2)g(\lambda )$$

(14)

Integration of corresponding differential equations, gives us:

$$\Psi =(1-{\eta }^2)(-\frac{1}{2}\lambda C_1+\frac{1}{2}{C}_2(({\lambda }^2-1)arcth(\lambda )-\lambda )+C_3({\lambda }^2-1))$$

(15)

In elliptical coordinates, the stream function takes the form:

$$\Psi ={\sin }^2({\xi }_2)(-\frac{1}{2}{C}_1\cosh ({\xi }_1)+\frac{1}{2}{C}_2({\sinh }^2({\xi }_1)arcth(\cosh ({\xi }_1))-\cosh ({\xi }_1))+C_3{\sinh }^2({\xi }_1))$$

(16)

A detailed derivation of Formula (15) is given in the Appendix A.

It is worth noting that a similar technique for constructing solutions was previously used to describe the flow outside a solid body in the form of a spheroid during its motion in a viscous fluid [31].

To complete the process of constructing the Stokes stream function defining the fluid flow inside the bubble we need to find the coefficients $C_1$, $C_2$, $C_3$ in the expression (16) that satisfy the boundary conditions.

Due to the peculiarity of constructing the stream function in the form (16), boundary condition (10) will be satisfied automatically.

From the condition on the segment between the foci of the ellipse (11), we obtain linear equations for the coefficients:

$$C_1+C_2=0$$

(17)

From condition (9) we get:

$$-\frac{1}{2}{\lambda }_0{C}_1+\frac{1}{2}{C}_2(({\lambda }_0{}^2-1)arcth({\lambda }_0)-{\lambda }_0)+C_3({\lambda }_0{}^2-1)=0$$

(18)

where ${\lambda }_0=\cosh ({\xi }_0)$, the value ${\xi }_1={\xi }_0$ defines the boundary of the spheroid.

Equations (17) and (18) define two linear equations for three unknown constants. Thus, one of the constants $C_1$, $C_2$, $C_3$ remains free, which makes it possible to vary the velocity of the border.

It should be noted that due to axial symmetry, the problem of constructing a solution inside an ellipse is reduced to the problem of constructing a solution in its half. Due to the peculiarity of the elliptical coordinate system, the Stokes stream functions given in different halves of the ellipse (Figure 4) will be symmetric about the axis $OZ$ (functions for different parts will have the same modulus and the opposite sign). This will ensure the fulfillment of the boundary conditions and the continuity condition of the stream function and its derivatives on the axis $OZ$.

4. Results and Discussion

The obtained analytical solution (16) opens up an opportunity for modeling of fluid flow inside the spheroid. It is worth noting that functions of the form (16) impose specific restrictions on the velocity function at the boundary. Due to the presence of the sine of the coordinate ${\xi }_2$ in Formula (16), the flow velocity function tends to zero at the ends of the ellipse and increases at its middle part. However, this feature is natural for the Taylor flows.

Let us consider an example of such a flow, given by an analytical stream function for a certain choice of constants in Formula (16). Velocity function at the boundary $S_1$ is shown in Figure 6. Flow streamlines are shown in Figure 7. Streamlinesin this example correspond to the following coefficients in (16): $C_1=1$, $C_2=-1$, $C_3=0.272$.

A flow with a similar set of parameters can be observed in the by-pass flow mode in microchannels, as well as inside a bubble moving far from the channel walls. In this type of flow, streamlines are around the bubble and are not closed, as shown in Figure 2. This feature of the flow leads to the appearance of shear stresses at the interface between liquids, acting from the nose of the bubble to its tail [32,33], which create circulation inside the bubble (Figure 7).

The analytical solution (16) can be used to simulate a three-dimensional axisymmetric flow between two confocal spheroids. In this case, the normal velocity at the boundary of the inner spheroid should be equal to zero. Condition (17) must be replaced by a condition that ensures the equality of the stream function to zero at the boundary of the inner spheroid:

$$-\frac{1}{2}{C}_1{\lambda }_1+\frac{1}{2}{C}_2(({\lambda }_1{}^2-1)arcth({\lambda }_1)-{\lambda }_1)+C_3({\lambda }_1{}^2-1)=0$$

(19)

where ${\lambda }_1=\cosh ({\xi }^{\ast })$, the value ${\xi }_1={\xi }^{\ast }$ defines the boundary of the inner spheroid.

Figure 8 shows the streamlines for the flow between two spheroids. The velocity function at the boundary of the spheroids is shown in Figure 9. The upper function (highlighted in blue) corresponds to the velocity on the outer spheroid, the bottom function (highlighted in red) corresponds to the velocity on the inner spheroid. Figures from this example correspond to the following coefficients in (16): $C_1=1$, $C_2=-1.196$, $C_3=0.385$.

It should be noted that a similar problem of the Stokes flow between two cylinders with an elliptical profile was previously considered in [26].

5. Conclusions

The geometric shape of the Taylor bubble can naturally be approximated by a spheroid of revolution. Therefore, a comparison of Taylor flows with axisymmetric Stokes flows inside a spheroid is quite applicable, despite the fact that the actual shape of the bubble can be more complicated due to the presence of microwaves on its surface.

This work is devoted to the derivation of exact analytical solutions of the Stokes equations for the model of axisymmetric flows inside the Taylor bubble. These solutions can be used as a tool for assessment of the numerical algorithms quality by comparing the result of the numerical algorithm with exact analytical solution. The advantage of this evaluation method is that it excludes the possibility of error accumulation which can occur in the case of comparing numerical algorithms with each other.