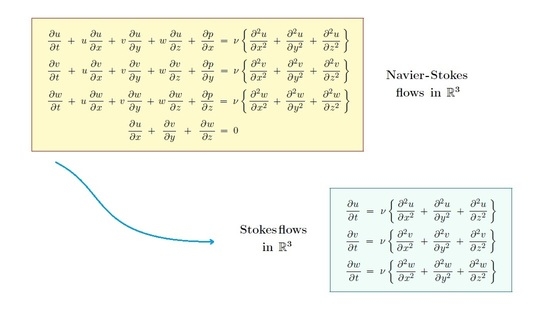
A Note on Stokes Approximations to Leray Solutions of the Incompressible Navier–Stokes Equations in ℝn
Abstract
:1. Introduction
2. Proof of Theorem 1
3. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Leray, J. Essai sur le mouvement d’un fluide visqueux emplissant l’espace. Acta Math. 1934, 63, 193–248. [Google Scholar] [CrossRef]
- Kreiss, H.-O.; Lorenz, J. Initial-Boundary Value Problems and the Navier-Stokes Equations; Academic Press: New York, NY, USA, 1989. [Google Scholar]
- Ladyzhenskaya, O.A. The Mathematical Theory of Viscous Incompressible Flows, 2nd ed.; Gordon and Breach: New York, NY, USA, 1969. [Google Scholar]
- Robinson, J.C.; Rodrigo, J.L.; Sadowski, W. The Three-Dimensional Navier-Stokes Equations; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Sohr, H. The Navier-Stokes Equations; Birkhäuser: Basel, Switzerland, 2001. [Google Scholar]
- Temam, R. Navier-Stokes Equations: Theory and Numerical Analysis; AMS/Chelsea: Providence, RI, USA, 1984. [Google Scholar]
- Silva, P.B.E.; Zingano, J.P.; Zingano, P.R. A note on the regularity time of Leray solutions to the Navier-Stokes equations. J. Math. Fluid Mech. 2019, 21, 8. [Google Scholar] [CrossRef]
- Brandolese, L.; Schonbek, M.E. Large time behavior of the Navier-Stokes flow. In Handbook of Mathematical Analysis in Mechanics of Viscous Fluids, Part I; Giga, Y., Novotny, A., Eds.; Springer: New York, NY, USA, 2018. [Google Scholar]
- Galdi, G.P. An introduction to the Navier-Stokes initial-boundary problem. In Fundamental Directions in Mathematical Fluid Dynamics; Galdi, G.P., Heywood, J.G., Rannacher, R., Eds.; Birkhauser: Basel, Switzerland, 2000; pp. 1–70. [Google Scholar]
- Lorenz, J.; Zingano, P.R. The Navier-Stokes equations for incompressible flows: Solution properties at potential blow-up times. Bol. Soc. Paran. Mat. 2015, 35, 127–158. [Google Scholar]
- Niche, C.J.; Schonbek, M.E. Decay characterization of solutions to dissipative equations. J. Lond. Math. Soc. 2015, 91, 573–595. [Google Scholar] [CrossRef] [Green Version]
- Kajikiya, R.; Miyakawa, T. On the L2 decay of weak solutions of the Navier-Stokes equations in ℝn. Math. Z. 1986, 192, 135–148. [Google Scholar] [CrossRef]
- Kato, T. Strong Lp-solutions of the Navier-Stokes equations in ℝm, with applications to weak solutions. Math. Z. 1984, 187, 471–480. [Google Scholar] [CrossRef]
- Kreiss, H.-O.; Hagstrom, T.; Lorenz, J.; Zingano, P.R. Decay in time of incompressible flows. J. Math. Fluid Mech. 2003, 5, 231–244. [Google Scholar] [CrossRef]
- Masuda, K. Weak solutions of the Navier-Stokes equations. Tôhoku Math. J. 1984, 36, 623–646. [Google Scholar] [CrossRef]
- Oliver, M.; Titi, E.S. Remark on the rate of decay of higher order derivatives for solutions to the Navier-Stokes equations in ℝn. J. Funct. Anal. 2000, 172, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Schonbek, M.E. Large time behaviour of solutions of the Navier-Stokes equations. Commun. Partial Differ. Equ. 1986, 11, 733–763. [Google Scholar] [CrossRef]
- Schonbek, M.E. Large time behaviour of solutions to the Navier-Stokes equations in Hm spaces. Commun. Partial Differ. Equ. 1995, 20, 103–117. [Google Scholar] [CrossRef]
- Schonbek, M.E.; Wiegner, M. On the decay of higher-order norms of the solutions of Navier-Stokes equations. Proc. R. Soc. Edinb. Sect. A 1996, 126, 677–685. [Google Scholar] [CrossRef]
- Wiegner, M. Decay results for weak solutions of the Navier-Stokes equations on ℝn. J. Lond. Math. Soc. 1987, 35, 303–313. [Google Scholar] [CrossRef]
- Zhou, Y. A remark on the decay of solutions to the 3-D Navier-Stokes equations. Math. Methods Appl. Sci. 2007, 30, 1223–1229. [Google Scholar] [CrossRef]
- Gallay, T.; Wayne, C.E. Long-time asymptotics of the Navier-Stokes and vorticity equations on ℝ3. Philos. Trans. R. Soc. Lond. 2002, 360, 2155–2188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyakawa, T.; Schonbek, M.E. On optimal decay rates for weak solutions to the Navier-Stokes equations in ℝn. Math. Bohem. 2001, 126, 443–455. [Google Scholar] [CrossRef]
- Brandolese, L. Space-time decay of Navier-Stokes flows invariant under rotations. Math. Ann. 2004, 329, 685–706. [Google Scholar] [CrossRef] [Green Version]
- Gallay, T.; Wayne, C.E. Invariant manifolds and the long-time asymptotics of the Navier-Stokes and vorticity equations on ℝ2. Arch. Rat. Mech. Anal. 2002, 163, 209–258. [Google Scholar] [CrossRef] [Green Version]
- Rigelo, J.C.; Schütz, L.; Zingano, J.P.; Zingano, P.R. Leray’s problem for the Navier-Stokes equations revisited. C. R. Math. 2016, 354, 503–509. [Google Scholar] [CrossRef]
- Schütz, L.; Zingano, J.P.; Zingano, P.R. On the supnorm form of Leray’s problem for the incompressible Navier-Stokes equations. J. Math. Phys. 2015, 56, 071504. [Google Scholar] [CrossRef] [Green Version]
- Hagstrom, T.; Lorenz, J.; Zingano, J.P.; Zingano, P.R. On two new inequalities for Leray solutions of the Navier-Stokes equations in ℝn. J. Math. Anal. Appl. 2020, 483, 123601. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigelo, J.C.; Zingano, J.P.; Zingano, P.R. A Note on Stokes Approximations to Leray Solutions of the Incompressible Navier–Stokes Equations in ℝn. Fluids 2021, 6, 340. https://doi.org/10.3390/fluids6100340
Rigelo JC, Zingano JP, Zingano PR. A Note on Stokes Approximations to Leray Solutions of the Incompressible Navier–Stokes Equations in ℝn. Fluids. 2021; 6(10):340. https://doi.org/10.3390/fluids6100340
Chicago/Turabian StyleRigelo, Joyce C., Janaína P. Zingano, and Paulo R. Zingano. 2021. "A Note on Stokes Approximations to Leray Solutions of the Incompressible Navier–Stokes Equations in ℝn" Fluids 6, no. 10: 340. https://doi.org/10.3390/fluids6100340
APA StyleRigelo, J. C., Zingano, J. P., & Zingano, P. R. (2021). A Note on Stokes Approximations to Leray Solutions of the Incompressible Navier–Stokes Equations in ℝn. Fluids, 6(10), 340. https://doi.org/10.3390/fluids6100340