Liquid Films Falling Down a Vertical Fiber: Modeling, Simulations and Experiments
Abstract
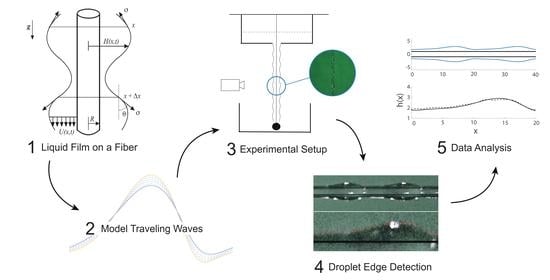
:1. Introduction
1.1. Background
1.2. Problem Overview and Approach
2. Model Derivation via Control Volume Analysis
2.1. Fully-Developed Flow
2.1.1. Plug Flow
2.1.2. Viscous Laminar Flow
2.2. Control Volume Analysis
2.3. Laminar Flow Case
2.4. Summary
2.5. Relation to Previous Two-Equation Models
3. Linear Stability Analysis
4. Simulations
5. Experimental Results
5.1. Experiment Setup
5.2. Observations
6. Numerical Data Analysis
7. Discussion
8. Summary
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Quéré, D.; di Meglio, J.M.; Brochard-Wyart, F. Making van der Waals films on fibers. EPL (Europhys. Lett.) 1989, 10, 335. [Google Scholar] [CrossRef]
- Quéré, D. Thin films flowing on vertical fibers. EPL (Europhys. Lett.) 1990, 13, 721. [Google Scholar] [CrossRef]
- Quéré, D. Fluid coating on a fiber. Annu. Rev. Fluid Mech. 1999, 31, 347–384. [Google Scholar] [CrossRef]
- Giorgiutti-Dauphiné, F.; Duprat, C.; Ruyer-Quil, C.; Hulin, J.P.; Trevelyan, P.M.; Kalliadasis, S. Experimental and numerical study of film flows down fibers at moderate Reynolds numbers. In Proceedings of the APS Division of Fluid Dynamics Meeting Abstracts, Tampa Bay, FL, USA, 19–21 November 2006; Volume 59, p. HD–002. [Google Scholar]
- Halpern, D.; Wei, H.H. Slip-enhanced drop formation in a liquid falling down a vertical fibre. J. Fluid Mech. 2017, 820, 42–60. [Google Scholar] [CrossRef]
- Nozaki, T.; Kaji, N.; Mori, Y.H. Heat transfer to a liquid flowing down vertical wires hanging in a hot gas stream: An experimental study of a new means of thermal energy recovery. In Proceedings of the International Heat Transfer Conference Digital Library, Kyongju, Korea, 23–28 August 1998; Begell House Inc.: Danbury, CT, USA, 1998. [Google Scholar]
- Zeng, Z.; Sadeghpour, A.; Warrier, G.; Ju, Y.S. Experimental study of heat transfer between thin liquid films flowing down a vertical string in the Rayleigh-Plateau instability regime and a counterflowing gas stream. Int. J. Heat Mass Transf. 2017, 108, 830–840. [Google Scholar] [CrossRef] [Green Version]
- Sadeghpour, A.; Zeng, Z.; Ji, H.; Ebrahimi, N.D.; Bertozzi, A.; Ju, Y. Water vapor capturing using an array of traveling liquid beads for desalination and water treatment. Sci. Adv. 2019, 5, eaav7662. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sadeghpour, A.; Zeng, Z.; Ju, Y.S. Effects of nozzle geometry on the fluid dynamics of thin liquid films flowing down vertical strings in the Rayleigh–Plateau regime. Langmuir 2017, 33, 6292–6299. [Google Scholar] [CrossRef] [Green Version]
- Kalliadasis, S.; Chang, H.C. Drop formation during coating of vertical fibres. J. Fluid Mech. 1994, 261, 135–168. [Google Scholar] [CrossRef]
- Ruyer-Quil, C.; Kalliadasis, S. Wavy regimes of film flow down a fiber. Phys. Rev. E 2012, 85, 046302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, L.; Hinch, J. The velocity of large viscous drops falling on a coated vertical fibre. J. Fluid Mech. 2013, 737, 232–248. [Google Scholar] [CrossRef]
- Ji, H.; Sadeghpour, A.; Ju, Y.S.; Bertozzi, A.L. Modelling film flows down a fibre influenced by nozzle geometry. J. Fluid Mech. 2020, 901, R6. [Google Scholar] [CrossRef]
- Frenkel, A. Nonlinear theory of strongly undulating thin films flowing down vertical cylinders. EPL (Europhys. Lett.) 1992, 18, 583. [Google Scholar] [CrossRef]
- Chang, H.C.; Demekhin, E.A. Mechanism for drop formation on a coated vertical fibre. J. Fluid Mech. 1999, 380, 233–255. [Google Scholar] [CrossRef]
- Marzuola, J.L.; Swygert, S.R.; Taranets, R. Nonnegative weak solutions of thin-film equations related to viscous flows in cylindrical geometries. J. Evol. Equ. 2019, 2019, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Ji, H.; Taranets, R.; Chugunova, M. On travelling wave solutions of a model of a liquid film flowing down a fibre. arXiv 2020, arXiv:2006.04994. [Google Scholar]
- Craster, R.; Matar, O. On viscous beads flowing down a vertical fibre. J. Fluid Mech. 2006, 553, 85–105. [Google Scholar] [CrossRef]
- Kliakhandler, I.; Davis, S.H.; Bankoff, S. Viscous beads on vertical fibre. J. Fluid Mech. 2001, 429, 381–390. [Google Scholar] [CrossRef]
- Chinju, H.; Uchiyama, K.; Mori, Y.H. String-of-beads flow of liquids on vertical wires for gas absorption. AIChE J. 2000, 46, 937–945. [Google Scholar] [CrossRef]
- Duprat, C.; Ruyer-Quil, C.; Kalliadasis, S.; Giorgiutti-Dauphiné, F. Absolute and convective instabilities of a viscous film flowing down a vertical fiber. Phys. Rev. Lett. 2007, 98, 244502. [Google Scholar] [CrossRef] [Green Version]
- Duprat, C.; Ruyer-Quil, C.; Giorgiutti-Dauphiné, F. Spatial evolution of a film flowing down a fiber. Phys. Fluids 2009, 21, 042109. [Google Scholar] [CrossRef] [Green Version]
- Ding, Z.; Liu, Z.; Liu, R.; Yang, C. Breakup of ultra-thin liquid films on vertical fiber enhanced by Marangoni effect. Chem. Eng. Sci. 2019, 199, 342–348. [Google Scholar] [CrossRef]
- Ji, H.; Falcon, C.; Sadeghpour, A.; Zeng, Z.; Ju, Y.; Bertozzi, A. Dynamics of thin liquid films on vertical cylindrical fibres. J. Fluid Mech. 2019, 865, 303–327. [Google Scholar] [CrossRef]
- Reisfeld, B.; Bankoff, S. Non-isothermal flow of a liquid film on a horizontal cylinder. J. Fluid Mech 1992, 236, 167196. [Google Scholar] [CrossRef]
- Trifonov, Y.Y. Steady-state traveling waves on the surface of a viscous liquid film falling down on vertical wires and tubes. AIChE J. 1992, 38, 821–834. [Google Scholar] [CrossRef]
- Ruyer-Quil, C.; Treveleyan, P.; Giorgiutti-Dauphiné, F.; Duprat, C.; Kalliadasis, S. Modelling film flows down a fibre. J. Fluid Mech. 2008, 603, 431–462. [Google Scholar] [CrossRef]
- Ruyer-Quil, C.; Trevelyan, S.; Giorgiutti-Dauphiné, F.; Duprat, C.; Kalliadasis, S. Film flows down a fiber: Modeling and influence of streamwise viscous diffusion. Eur. Phys. J. Spec. Top. 2009, 166, 89–92. [Google Scholar] [CrossRef]
- Novbari, E.; Oron, A. Energy integral method model for the nonlinear dynamics of an axisymmetric thin liquid film falling on a vertical cylinder. Phys. Fluids 2009, 21, 062107. [Google Scholar] [CrossRef]
- Liu, R.; Ding, Z. Coating flows down a vertical fibre: Towards the full Navier–Stokes problem. J. Fluid Mech. 2021, 914, A30. [Google Scholar] [CrossRef]
- Alekseenko, S.; Nakoryakov, V.; Pokusaev, B. Wave formation on vertical falling liquid films. Int. J. Multiph. Flow 1985, 11, 607–627. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Münch, A.; Shearer, M. Undercompressive shocks in thin film flows. Phys. D Nonlinear Phenom. 1999, 134, 431–464. [Google Scholar] [CrossRef]
- Bertozzi, A.L.; Shearer, M. Existence of undercompressive traveling waves in thin film equations. SIAM J. Math. Anal. 2000, 32, 194–213. [Google Scholar] [CrossRef] [Green Version]
- Bertozzi, A.L.; Münch, A.; Shearer, M.; Zumbrun, K. Stability of compressive and undercompressive thin film travelling waves. Eur. J. Appl. Math. 2001, 12, 253–291. [Google Scholar] [CrossRef] [Green Version]
- Diamante, L.M.; Lan, T. Absolute viscosities of vegetable oils at different temperatures and shear rate range of 64.5 to 4835 s−1. J. Food Process. 2014, 2014, 1–6. [Google Scholar] [CrossRef] [Green Version]










| Hole Size (mm) | Flow Rate (g/s) | Droplet Size (mm) | Gap Size (mm) | Droplet Velocity (mm/s) |
|---|---|---|---|---|
| 1.6 | 0.0067 | 3-5 | various | 10 |
| 2 | 0.0366 | 4 | 3 | 15 |
| 2.4 | 0.0833 | 5 | 7 | 30 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, Y.; Nadim, A.; Duvvoori, L.; Chugunova, M. Liquid Films Falling Down a Vertical Fiber: Modeling, Simulations and Experiments. Fluids 2021, 6, 281. https://doi.org/10.3390/fluids6080281
Ruan Y, Nadim A, Duvvoori L, Chugunova M. Liquid Films Falling Down a Vertical Fiber: Modeling, Simulations and Experiments. Fluids. 2021; 6(8):281. https://doi.org/10.3390/fluids6080281
Chicago/Turabian StyleRuan, Yadong, Ali Nadim, Lekha Duvvoori, and Marina Chugunova. 2021. "Liquid Films Falling Down a Vertical Fiber: Modeling, Simulations and Experiments" Fluids 6, no. 8: 281. https://doi.org/10.3390/fluids6080281
APA StyleRuan, Y., Nadim, A., Duvvoori, L., & Chugunova, M. (2021). Liquid Films Falling Down a Vertical Fiber: Modeling, Simulations and Experiments. Fluids, 6(8), 281. https://doi.org/10.3390/fluids6080281