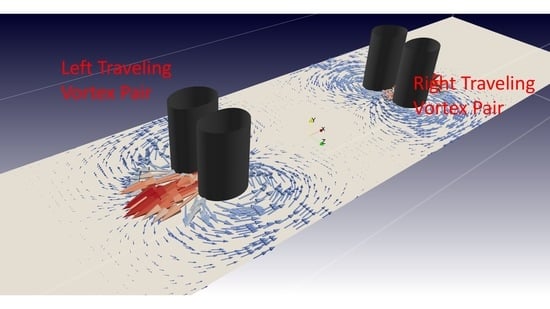
Numerical Simulation and Linearized Theory of Vortex Waves in a Viscoelastic, Polymeric Fluid

Abstract

In a high viscosity, polymeric fluid initially at rest, the release of elastic energy produces vorticity in the form of coherent motions (vortex rings). Such behavior may enhance mixing in the low Reynolds number flows encountered in microfluidic applications. In this work, we develop a theory for such flows by linearizing the governing equations of motion. The linear theory predicts that when elastic energy is released in a symmetric manner, a wave of vorticity is produced with two distinct periods of wave motion: (1) a period of wave expansion and growth extending over a transition time scale, followed by (2) a period of wave translation and viscous decay. The vortex wave speeds are predicted to be proportional to the square root of the initial fluid tension, and the fluid tension itself scales as the viscosity. Besides verifying the predictions of the linearized theory, numerical solutions of the equations of motion for the velocity field, obtained using a pseudo-spectral method, show that the flow is composed of right- and left-traveling columnar vortex pairs, called vortex waves for short. Wave speeds obtained from the numerical simulations are within 1.5% of those from the linear theory when the assumption of linearity holds. Vortex waves are found to decay on a time scale of the order of the vortex size divided by the solution viscosity, in reasonable agreement with the analytical solution of the linearized model for damped vortex waves. When the viscoelastic fluid is governed by a nonlinear spring model, as represented by the Peterlin function, wave speeds are found to be larger than the predictions of the linear theory for small polymer extension lengths.

1. Introduction

Recently [1], it was shown theoretically and through numerical simulations that coherent vortex motions can be generated by the release of elastic energy in a viscoelastic, polymeric fluid initially at rest. That work was motivated by exploring novel mechanisms for the enhancement of mixing in low Reynolds number flows, including microflows, as well as the possibility of understanding the mechanisms underlying the generation of chaotic fluid motions [2,3] in such flows. Elastic stress gradients in viscoelastic flows of dilute polymer solutions were shown to generate torques on fluid elements, which in turn generate coherent vortex motions (e.g., vortex rings). In the situation where the initial elastic stress field was spatially symmetric, two vortex rings were shown to form and move in opposite directions before being dissipated by viscous effects. In addition, the strength of the vortex motions followed the trends predicted by the theory. However, important aspects of the kinematics and dynamics associated with these coherent vortical structures were not explored in [1]. In particular, the speed of translation of these vortices was not investigated. In this work, we show that the release of elastic energy generates vorticity that propagates as a wave, whose speed is governed by the initial stress field in the fluid.

Only recently have viscoelastic stresses been considered as a source of fluid torques [4,5]. In that work, it was shown that torques arising from viscoelastic stresses can act to reduce the strength of hairpin vortices in high Reynolds number turbulent flows. It was shown that viscoelastic forces generate torque in a direction opposite that of drag-producing vortices, reducing the rotational energy of these structures. The current effort explores the nature of such forces at low Reynolds numbers and in flow situations that do not involve complex fluid motions that may arise from instabilities. Instead, we explore ways in which viscoelastic stresses can produce vorticity in a polymeric fluid as opposed to ways in which these stresses can affect the flow. Vorticity produced in this way can be understood by considering a force per unit volume, given by the divergence of the total stress in the fluid, the latter composed of both Newtonian and elastic components. Since this force is not conservative and therefore has a non-zero curl, vorticity can be produced by such a stress field of the proper spatial form. It follows that polymeric stress gradients can give rise to fluid torques and therefore also to vorticity. As discussed in Handler et al. [1], the formation of coherent vorticity in this manner can be understood using an analogy of a stretched piece of rubber being suddenly cut.

The release of elastic energy and its subsequent conversion to fluid motion has been considered by Min et al. [6] as a possible explanation of the long-standing problem concerning the mechanism by which polymer addition reduces drag in turbulent flows [7,8,9,10,11,12,13,14,15,16]. They show, through direct numerical simulations of turbulence, that drag reduction occurs when the polymer relaxation time is large. In this case, kinetic energy near a no-slip wall is absorbed by polymers and is thus stored as elastic energy. Subsequently, these fluid elements with stored elastic energy are transported upward, away from the near-wall region, where their elastic energy is transformed into kinetic energy. A schematic illustrating this mechanism can be found in their paper [6]. In related work, De Gennes [17] contends that elastic rarefaction and shock waves may play a role in drag reduction. In both of these works, the classic Kolmogorov cascade is thought to be modified to some extent by the existence of elasticity. These new ideas emphasize the direct effects of elasticity and energy dynamics, complementing the classical theories [10] that emphasize the increase in effective viscosity due to polymer addition.

We are further motivated by fundamental developments in microflows, which are driven by a wide variety of important applications, such as those in biotechnology [18,19], bio-sensor development [20], and in the design of micro-electro-mechanical systems (MEMS) [21,22]. Many of these applications are concerned with flows in which the Reynolds numbers are small and the Peclet numbers are large ($Re\ll 1$, and $Pe\gg 1$). Low Reynolds numbers ensure that inertial instabilities are absent, while large Peclet numbers imply that diffusion rates among species are slow. Under these conditions, mixing is difficult or impossible to achieve. Therefore, if mixing is the desired goal, novel approaches [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47] must be employed to enhance transport. A detailed review of the underlying physics associated with these flows is given by Squires and Quake [48] and Stone et al. [49]. They emphasize that as the length scale of these devices is reduced, the physical processes that were applicable at larger scales are reduced in importance, as other processes (e.g., capillarity, buoyancy, and electro-chemical processes) come into play. In particular, it might be expected that the effects of fluid elasticity would not be of importance in such low Reynolds number flows. However, instabilities due solely to fluid elasticity have been found in a wide variety of flows [50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]. A detailed review of the relationship between the current work and [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66] can be found in the Introduction of [1]. More recent experiments [2,3] have discovered chaotic flows of a viscoelastic fluid within microchannels.

The goal of the present work is to show that coherent vortex motions created in the manner described above are in fact a manifestation of a wave of vorticity, which we called a vortex wave. We start from the equations of motion for an incompressible fluid coupled to the FENE-P model [67,68], a widely used model for polymer dynamics. These equations are linearized about a state of rest and constant polymer stress. The resulting linearized system is shown to give rise to a damped wave equation for the vorticity field, which predicts that the wave speed is proportional to the square root of the initial elastic stress in the fluid, which in turn scales with viscosity. Predictions from the linearized theory are compared to direct numerical simulations, from which the entire velocity and vorticity field is obtained.

The remainder of this paper contains the following sections: 2. Vorticity Generation in a Viscoelastic Fluid, 3. Linearized Equations for Vortex Waves, 4. Numerical Methods, 5. Flow Visualization and Kinematics, 6. Linearized Wave Equation and the Undamped Solution, 7. Viscous Effects, 8. Vortex Wave Speed, and 9. Summary and Discussion. In Section 2, we describe the general equations of motion for an incompressible fluid, along with the FENE-P model, which governs the polymer dynamics. In addition, the mechanism by which vorticity can be generated in a viscoelastic fluid is presented. A linearization of these equations is performed in Section 3. This results in a damped wave equation for the vorticity, which predicts the existence of a vortex wave whose speed is proportional to the square root of the initial tension in the fluid. The content of Section 3 is subsequently referred to as the linearized theory. In Section 4 and Section 5, the numerical methods used to perform a series of simulations are discussed, followed by a description of the vortex kinematics. We use the term numerical simulation to refer to the numerical solution of the full three-dimensional nonlinear equations of fluid motion using pseudo-spectral methods, which we also refer to as a direct numerical simulation (DNS). Flow visualization reveals the existence of two columnar vortex pairs (vortex waves) that propagate in opposite directions. An analysis of the kinematics shows that the vortex wave manifests itself first by a period of expansion followed by a period of translation, a result that agrees well with an analytical model of an undamped wave given in Section 6. Here, the term analytical model or model refers to a simplified version of the linearized equations derived in Section 3. In Section 7, an analytical model that includes the effects of viscosity is shown to predict the decay of the vortex wave in reasonable agreement with numerical simulations. Section 8 focusses on the effects of wave amplitude, initial fluid tension, and the maximum polymer extensional length on the speed of the vortex wave. Here, it is shown, for waves of low amplitude and also governed by a linear spring model, that wave speeds determined from the numerical simulations are in excellent agreement with speeds predicted from the theory developed in Section 3. When the full FENE-P model is used, it is found that wave speeds are higher than for linear springs when the maximum extensional polymer length is small. Finally, in the Summary and Discussion section, we discuss the possible applications of vortex waves in promoting mixing in highly viscous flows.

2. Vorticity Generation in a Viscoelastic Fluid

The velocity field is governed by the momentum equation and the equation of continuity for an incompressible fluid given by

$$\rho \frac{D\mathit{V}}{Dt}=-\mathbf{\nabla }\mathrm{P}+\mathbf{\nabla }·T$$

(1)

and

$$\mathbf{\nabla }·\mathit{V}=0,$$

(2)

where $D/Dt$=$\raisebox{1ex}{$ \partial $}\!\left/ \!\raisebox{-1ex}{$\partial t$}\right.+\mathit{V}·\mathbf{\nabla }\mathit{V}$ is the material derivative; $\mathit{V}=\left(u,v,w\right)=\left(u_1,u_2,u_3\right)$ is the fluid velocity with components in the $x,y,z$or $x_1,x_2,x_3$ directions; $P$ is the pressure; $T$ is the stress tensor; and $\rho$ is the density. The right-handed $x,y,z$ coordinate system is used interchangeably with the terms streamwise, vertical or wall normal, and spanwise, respectively. For a dilute polymer solution, the stress is decomposed into a Newtonian component, ${\mathsf{\tau }}^n$, and a polymeric component, ${\mathsf{\tau }}^p$, as follows:

$$T={\tau }^n+{\mathsf{\tau }}^p ,$$

(3)

where ${\mathsf{\tau }}^n=2{\mu }_0\beta S, {\mu }_0$ is the solution viscosity, $\beta$ is the ratio of the solvent viscosity to the solution viscosity, and $S$ is the rate-of-strain tensor. A widely used model for the polymeric stress of a so-called FENE-P fluid [67,68] is given by

$${\mathsf{\tau }}^p=\frac{{\mu }_0\left(1-\beta \right)}{\lambda }\left[f\left(R\right)C-I\right],$$

(4)

where $\lambda$ is the polymer relaxation time; $C$ is the conformation tensor defined as the average over all possible molecular configurations of the product of the end-to-end vectors associated with the polymer molecular length; $R=\sqrt{\mathrm{tr}\left(C\right)}$; $I$ is the unit tensor; and $f\left(R\right)=\left(L^2-3\right)/\left(L^2-R^2\right)$ is the Peterlin function, where $L$ is the maximum allowable molecular extension. In the equations above, and in all subsequent ones, $\mathit{C}, L,$ and $R$ are made nondimensional by the rest length, or square of the length as appropriate, of the polymer molecule.

In the FENE-P model, which is derived using a kinetic theory approach, the solvent is viewed as being populated with polymer molecules, each of which is thought of as a dumbbell consisting of two massless spheres connected by a spring. The solvent can stretch the dumbbells via viscous forces, which then react back on the fluid. When the Peterlin function is employed, the dumbbells are prevented from stretching to infinite lengths, which can be thought of as a nonlinear spring model. The FENE-P model has proven effective in recent years in exploring complex phenomena, such as the effect of polymer additives in fully turbulent flows, although some unrealistic aspects of the model have been discussed in recent work [69]. In this context, direct numerical simulations (DNS) [11,12,13,14,15] of such flows have been confirmed by experimental observations [7,8,9].

The evolution of the conformation tensor $\mathit{C}$ is governed by

$$\frac{D\mathit{C}}{Dt}=\mathit{C}·\mathbf{\nabla }\mathit{V}+{\left(\mathbf{\nabla }\mathit{V}\right)}^T·\mathit{C}-\frac{1}{\mathsf{\lambda }}\left[f\left(R\right)\mathit{C}-\mathit{I}\right]+D_p{\nabla }^2\mathit{C} ,$$

(5)

where $D_p$ is the polymer diffusivity. The first two terms on the right-hand side of Equation (5) represent the stretching and reorientation of polymer molecules by flow gradients, which are balanced by the third term, the spring relaxation term. The balance between stretching and relaxation implies that with no stretching, the polymers will relax back to their equilibrium length.

The details of how coherent vorticity can be generated in a viscoelastic fluid has been discussed previously [1]; therefore, here, we only summarize those results. The vorticity transport equation can be obtained by first taking the curl of Equation (1) while taking into account the decomposition given by Equation (3). For an incompressible fluid of constant density, the evolution equation for the vorticity $\Omega$ becomes

$$\frac{D\Omega }{Dt}=\left(\mathsf{\Omega }·\mathbf{\nabla }\right)\mathit{V}+{\nu }_0\beta {\nabla }^2\mathsf{\Omega }+{\rho }^{-1}\mathbf{\nabla }\times \left(\mathbf{\nabla }·{\mathit{\tau }}^{\mathit{p}}\right),$$

(6)

where the first term on the left side is the material derivative of the vorticity; on the right side, the first term represents the stretching and tilting of vorticity by velocity gradients; the second term represents diffusion of vorticity by viscosity; and the third term represents the generation of vorticity by polymeric stresses. Here, ${\nu }_0={\mu }_0/\rho$ is the kinematic viscosity of the solution. According to Equation (6), the last term can be interpreted as a source of vorticity caused by the force per unit volume, $\mathbf{\nabla }·{\mathit{\tau }}^{\mathit{p}}$. This term represents a net torque on fluid elements, creating local spin. For a fluid that is initially at rest ($\mathit{V}=\mathbf{0}$), each term in Equation (6) can be evaluated at time $t=0$, which gives

$${\left.\frac{\partial {\mathsf{\Omega }}_m}{\partial t}\right|}_{t=0}=\alpha f\frac{{\partial }^2{C}_{ji}}{\partial x_j\partial x_k}{ϵ}_{mki},$$

(7)

where

$$\alpha ={\nu }_0\left(1-\beta \right)/\lambda ,$$

(8)

and both $f$ and $C_{ji}$ are to be evaluated at time $t=0$. To arrive at Equation (7), the maximal allowable polymer length $L$ is assumed to be such that $L^2\gg \mathrm{tr}\left(C\right)$ so that $f$ is a constant. The derivation of Equation (7) is given in Appendix A. For simplicity and other reasons given below, we emphasize the results in which $f=1$, the case in which the polymeric spring can be considered linear. However, we also explore in a more limited way the case in which the full Peterlin model is employed. Equation (7) indicates that it is the gradients of the initial polymeric stress field that are directly responsible for vorticity production. It was shown [1] that when such stress gradients exist initially, coherent vorticity in the form of a pair of vortex rings is produced.

3. Linearized Equations for Vortex Waves

Insight can be gained concerning the connection between the elasticity inherent in the fluid and the existence of vortex waves by linearizing Equations (1)–(6). Here, we employ a familiar linearization procedure, borrowed from acoustics, where it is used to derive the wave equation from the nonlinear compressible form of the equations of motion [70]. For our purpose, we express the components of the velocity; vorticity; and the conformation tensor ($V_i,{\Omega }_i,C_{ji}$) and the pressure, $P,$ as follows:

$$V_i=V_i^0+u_i,$$

(9)

$${\Omega }_i={\Omega }_i^0+{\omega }_i,$$

(10)

$$C_{ji}=C_{ji}^0+c_{ji},$$

(11)

$$P=P^0+p,$$

(12)

where $V_i^0$, ${\Omega }_i^0$, $C_{ji}^0$, and $P^0$ are the average or mean values of the corresponding variables defined in a suitable manner (e.g., time or ensemble averaged), which are assumed to be spatially and temporally constant. The corresponding fluctuations are $u_i$, ${\omega }_i,c_{ji}$, and $p$. To arrive at a set of linearized equations, all fluctuating quantities are assumed small compared to their suitably defined mean values. In the above expressions, ${\Omega }_i^0\equiv {\partial }_k{V}_q^0{ϵ}_{ikq}$, and ${\omega }_i\equiv {\partial }_k{u}_q{ϵ}_{ikq}$, where in these expressions and hereafter, repeated indices imply summation. In addition, since we are interested in flows starting from rest, $V_i^0=0$ and ${\Omega }_i^0=0$. Introducing Equations (9)–(12) into the governing Equations (1)–(6), neglecting all higher order terms and assuming $f$is constant as discussed above, equations for the perturbations are obtained as follows:

$${\dot{u}}_i=-{\rho }^{-1}{\partial }_{i}p+\alpha f{\partial }_j{c}_{ji}+{\nu }_0\beta {𝛻}^2{u}_i,$$

(13)

$$\dot{{\omega }_m}=\alpha f{\partial }_k{\partial }_j{c}_{ji}{ϵ}_{mki}+{\nu }_0\beta {𝛻}^2{\omega }_m,$$

(14)

$${\partial }_i{u}_i=0,$$

(15)

$${\dot{c}}_{ji}=C_{jk}^0{\partial }_k{u}_i+C_{ik}^0{\partial }_k{u}_j-\frac{f}{\lambda }{c}_{ji},$$

(16)

where here and subsequently, a dot over a variable represents partial differentiation with respect to time and ${\nabla }^2={\partial }_j^2={\partial }_j{\partial }_j$. An additional equation for the evolution of the mean value of the conformation tensor is also obtained as follows:

$${\dot{C}}_{ji}^0=-{\lambda }^{-1} \left[f{C}_{ji}^0-{\delta }_{ji}\right].$$

(17)

From Equation (17), it follows that when $\raisebox{1ex}{$\lambda $}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.\gg 1$, so that the polymer relaxation time is large relative to a characteristic flow time scale, τ, it can be assumed that $C_{ji}^0$ is essentially independent of time. Anticipating the existence of waves that travel at speed $c$, the flow time scale should be set to $\tau \sim \raisebox{1ex}{$d$}\!\left/ \!\raisebox{-1ex}{$c$}\right.$, where $d$ is the distance traveled by the wave during a given experiment or simulation. Under these circumstances, this scaling shows that the initial polymer stresses do not decay to any appreciable degree, an assumption that is implicit in Equations (13)–(16).

To obtain the governing equation for the vorticity fluctuations, ${\omega }_m$, we differentiate Equation (14) with respect to time yielding

$${\ddot{\omega }}_m=\alpha f{\partial }_k{\partial }_j{\dot{c}}_{ji}{ϵ}_{mki}+{\nu }_0\beta {\nabla }^2{\dot{\omega }}_m$$

(18)

Equation (16) for the fluctuations of the conformation tensor can then be substituted into the first term on the right-hand side of Equation (18) giving

$${\ddot{\omega }}_m=\alpha f{\partial }_k{\partial }_j\left(C_{jq}^0{\partial }_q{u}_i\right){ϵ}_{mki}+\alpha f{\partial }_k{\partial }_j\left(C_{iq}^0{\partial }_q{u}_j\right){ϵ}_{mki}+{\nu }_0\beta {\nabla }^2{\dot{\omega }}_m-\raisebox{1ex}{$\alpha f^2$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.{\partial }_k{\partial }_j{c}_{ji}{ϵ}_{mki}.$$

(19)

This equation can be simplified by noting that the second term on the right-hand side is zero owing to the incompressibility condition (Equation (15)). Further simplification can be obtained by using Equation (14) and ${\omega }_m\equiv {\partial }_k{u}_i{ϵ}_{mki}$ to obtain

$${\ddot{\omega }}_m=\left(\alpha f{C}_{jq}^0+\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.{\nu }_0\beta {\delta }_{jq}\right){\partial }_j{\partial }_q{\omega }_m+{\nu }_0\beta {\nabla }^2{\dot{\omega }}_m-\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.{\dot{\omega }}_m.$$

(20)

In this work, we are especially interested in waves traveling only in one direction, say $x_1$. In this case, Equation (20) becomes

$${\ddot{\omega }}_m=C^2\frac{{\partial }^2{\omega }_m}{\partial x_1^2}+{\nu }_0\beta {\nabla }^2{\dot{\omega }}_m-\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.{\dot{\omega }}_m,$$

(21)

where $C=\sqrt{\alpha f{C}_{11}^0+\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.{\nu }_0\beta }$. The last two terms on the right-hand side of Equation (21) can be identified as damping terms. If these two terms are neglected, Equation (21) reduces to

$${\ddot{\omega }}_m=C^2\frac{{\partial }^2{\omega }_m}{\partial x_1^2} ,$$

(22)

which is the wave equation for the propagation of the vorticity with speed $C$. For situations in which $\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.{\nu }_0\beta \ll \alpha f{C}_{11}^0$, which is the case in the situations we investigate through numerical simulations, the vortex wave speed can be accurately approximated by

$$C=\sqrt{\alpha f{C}_{11}^0}$$

(23)

This indicates (see Equation (4)) that the wave speed is proportional to the square root of the initial tensile stress in the fluid divided by density, which is analogous to the wave speed in a stretched string [70]. However, in contrast to a string, the wave speed also depends on the solution viscosity and the relaxation time through $\alpha$, as defined by Equation (8).

4. Numerical Methods

To test certain aspects of the theory of vortex wave generation, a series of direct numerical simulations were performed. For this purpose, Equations (1)–(5) were solved using a pseudo-spectral code [71] in a channel geometry in which all field variables are expanded in Fourier modes in the horizontal $\left(x-z\right)$ plane and in Chebyshev modes in the vertical $\left(y\right)$ direction. Spectral methods exhibit exponential convergence [72] and have been used with success in simulating fully developed turbulent flows [73]. The computational domain lengths were $L_x=4\pi , L_y=2$and $L_z=\pi$ in the $x,y,$ and $z$ directions, respectively, where these lengths have been made non-dimensional by the channel half-height, $l_y$. The coordinate system and geometry associated with this domain are shown in Figure 1A. In these simulations, vortex waves travel in the $x$-direction, with the $y$and $z$. directions perpendicular to this direction. There were $128\times 65\times 64$ grid nodes in the $x,y,$ and $z$directions, respectively. All relevant symbols used in this paper are listed in

Table A1. This table lists all relevant symbols used in this work. For each symbol, a definition is given followed by a designation of the symbol as dimensional (e.g., centimeters, seconds) or dimensionless.

Symbol	Definition	Units
$x,y,z$	Coordinates: the vortex waves travel in the x-direction, z is perpendicular to this direction, and y is the vertical direction (see Figure 1)	Dimensional
$x_1,x_2,x_3$	Scripted coordinates corresponding to $x,y,z$	Dimensional
$l_x,l_y,l_z$	Lengths of the computational domain in the $x$, $y$, and $z$ directions. $l_y$ is the half-height of the computational domain in the y-direction	Dimensional
$\overline{x},\overline{y},\overline{z}$	Coordinates x,y,z made dimensionless using $l_y$	Dimensionless
$L_x,L_y,L_z$	Computational domain lengths made dimensionless using $l_y$. Note that this definition leads to $L_y=2$.	Dimensionless
$t$	Time	Dimensional
$V,V_i$	Velocity and components of the velocity	Dimensional
$\mathsf{\Omega },{\mathsf{\Omega }}_i$	Vorticity and components of the vorticity	Dimensional
$C,C_{ji}$	Polymer conformation tensor and its components	Dimensionless. The conformation tensor is made dimensionless using the rest length of the polymer molecule
$P$	Fluid pressure	Dimensional
$V_i^0, u_i$	Average or mean value of the velocity (e.g., time or ensemble averaged) and its perturbation	Dimensional
${\mathsf{\Omega }}_i^0, {\omega }_i$	Average or mean value of the vorticity (e.g., time or ensemble averaged) and its perturbation	Dimensional
$C_{ji}^0, c_{ji}$	Average or mean value of the conformation tensor (e.g., time or ensemble averaged) and its perturbation	Dimensional
$P^0,p$	Average or mean value of the pressure (e.g., time or ensemble averaged) and its perturbation	Dimensional
${\nu }_0$	Solution viscosity	Dimensional
$\lambda$	Polymer relaxation time	Dimensional
$\beta$	Ratio of the solvent to the solution viscosity	Dimensionless
$\alpha$	Stress parameter. $\alpha ={\nu }_0\left(1-\beta \right)/\lambda$	Dimensional
$L$	Maximum possible extensional length made dimensionless using the polymer rest length	Dimensionless
$C$	Vortex wave speed. See definition directly following Equation (21).	Dimensional
$a$	Length associated with the region in which the fluid tension experiences a deficit. The region is a square with length $2a$ on each side. See Figure 1B.	Dimensional
$A$	$A=a/l_y$ In the simulations and theory, $A=0.25$. See Figure 1B.	Dimensionless
$T$	The transition time $T=$ a/C. Before this time, the vortex wave expands without translating. Translation occurs when $t>T.$	Dimensional
$T^{*}$	Dimensionless transition time, $T^{*}=$ $T{\nu }_0/a^2$.	Dimensionless
$\overline{t}$	Dimensionless time. $\overline{t}$ = $t{\nu }_0/a^2$.	Dimensionless
$\overline{C}$	Dimensionless vortex wave speed.$\overline{C}=Ca/{\nu }_0$.	Dimensionless
$C_{11}^0$	Initial value of the component of the conformation tensor, which is directly proportional to the fluid tension in the fluid.	Dimensionless
$f$	The Peterlin function. $f\left(R\right)=\left(L^2-3\right)/\left(L^2-R^2\right)$ where $R=\sqrt{\mathrm{tr}\left(\mathrm{C}\right)}$.	Dimensionless
${\epsilon }_0$	Amplitude of the polymer conformation deficit, which is proportional to the stress deficit.	Dimensionless
$N$	Amplitude parameter given by $N={\epsilon }_0/C_{11}^0$. When $N\ll 1$, the vortex wave can be considered linear.	Dimensionless
${\mathsf{\Omega }}_y$	Component of the vorticity in the vertical (y) direction.	Dimensional
$\overline{{\mathsf{\Omega }}_y}$	Dimensionless vertical vorticity where $\overline{{\mathsf{\Omega }}_y}={\mathsf{\Omega }}_y{a}^2/{\nu }_0$.	Dimensionless
$\tau$	translational time scale for a vortex wave	Dimensional
d	distance traveled by a vortex wave in time $\tau$	Dimensional
Q	amplitude of the source of the vortex wave	Dimensional

in Appendix B.

In terms of physical dimensions, the domain lengths in the $x$ and $z$ directions were $l_x=4\pi$cm and $l_z=\pi$ cm, and in the $y$-direction, the half-height was $l_y=1$ cm. The corresponding distances between grid nodes were $\Delta x=$ 9.82 $\times {10}^{-4}$ m and $\Delta z=$ 2.45 $\times {10}^{-4}$ m, respectively. In the $y$-direction, the use of Chebyshev polynomials results in a nonuniform grid. The smallest grid resolution occurs at the boundaries of the computational domain where $\Delta y=$ $1.2\times {10}^{-5}$ m, and at the center of the domain, the resolution was $\Delta y=4.91\times {10}^{-4}$ m. The grid resolution is therefore sub-millimeter in all three directions. The kinematic viscosity of the solution was ${\nu }_0=$ ${10}^{-4}$ m²/s, which is consistent with typical values used in experiments [3]. The code used in this work was thoroughly tested against analytic solutions for steady and unsteady viscoelastic laminar channel flow. In addition, the code gave good agreement with recent experiments [71] for heat transfer in a dilute polymer solution, and simulations of vortex rings using this algorithm were in agreement with theoretical predictions [1]. Furthermore, we examined the fields generated in these simulations and found no evidence of grid-scale oscillations, thereby assuring that our simulations were well resolved.

In these simulations, the fluid, which is initially at rest, is in a state of uniaxial tension, which can be specified by allowing the conformation tensor at $t=0$ to be $C_{11}=C_{11}^0$, where $C_{11}^0$ is a positive constant. A wave system can be generated by allowing the initial conformation field to possess spatial gradients. This can be accomplished by perturbing the stress field by letting $C_{11}=C_{11}^0-\epsilon ,$with $\epsilon >0$ and $<C_{11}^0$, which effectively creates a stress deficit in the fluid. The perturbation exists only in a small region of the domain such that $\epsilon ={\epsilon }_0$ where ${\epsilon }_0$ is a constant for ${\alpha }_2\ge x\ge {\alpha }_1$ and ${\alpha }_2\ge z\ge {\alpha }_1$ and $\epsilon =0$ outside this region. Note that the perturbation varies only in the horizontal ($x-z)$ plane and thus has no dependence on the vertical coordinate, $y$. For the other components of the conformation, we set the initial values of $C_{22}$ and$C_{33}$equal to constants and$C_{ji}=0$ for $i\ne j$. The location of the stress deficit relative to the computational domain is illustrated in Figure 1B.

The perturbation described above is capable of generating an imbalance in stress, which causes fluid particles to accelerate locally. For example, near $x={\alpha }_2$, the stress deficit will drive flow in the positive $x$ direction, whereas the fluid near $x={\alpha }_1$ will be driven in the opposite direction. This force field has the same effect as a spatially localized impulsive body force, which can readily be shown to create vorticity [74,75] (see also Figure 1 of [1]). This scenario can also be thought of as the release of elastic energy from a stretched rubber band that has been suddenly cut. Furthermore, the vorticity transport equation (Equation (6)) shows that torques on fluid elements can be produced by gradients in the elastic stress field, and for a fluid initially at rest, the rate at which vorticity is generated initially has a particularly simple form given by Equation (7). Since the perturbation in stress varies only in the horizontal plane, $C_{11}$ does not vary in the vertical ($x_2$) coordinate. In this case, Equation (7) indicates that only vertical vorticity can be generated as follows:

$${\left.\frac{\partial {\mathsf{\Omega }}_2}{\partial t}\right|}_{t=0}=\alpha f\frac{{\partial }^2{C}_{11}}{\partial x_1\partial x_3}.$$

(24)

On the top and bottom walls of the channel, shear-free conditions, $\raisebox{1ex}{$\partial V_1$}\!\left/ \!\raisebox{-1ex}{$\partial x_2$}\right.=\raisebox{1ex}{$\partial V_3$}\!\left/ \!\raisebox{-1ex}{$\partial x_2$}\right.=V_2=0$, were imposed on the velocity field and no flux [76] conditions, $\partial C_{ji}/\partial x_2$ = 0, were applied to the conformation. In all simulations described here, the ratio of the solvent viscosity to the solution viscosity was set to$\beta =0.5$, the polymer relaxation time was set such that $\raisebox{1ex}{$\lambda $}\!\left/ \!\raisebox{-1ex}{$\tau $}\right.\gg 1$, and the Schmidt number for the polymer was $S{c}_p=\raisebox{1ex}{$v_0$}\!\left/ \!\raisebox{-1ex}{$D_p$}\right.$ = 6. With this choice of relaxation time and Schmidt number, we ensure that that the effects of polymeric diffusion are small. The nature of the forcing described above, together with the boundary conditions, give rise to two columnar vortex pairs, one traveling to the left and one to the right. Each vortex thus produced will have only vertical vorticity, ${\mathsf{\Omega }}_2$. We note that even though this flow is strictly two dimensional, we used a three-dimensional code for reasons of convenience.

5. Flow Visualization and Kinematics

A visualization of the velocity and vorticity of the flow associated with a vortex wave obtained from the numerical simulations is shown in Figure 1A. As described above, elastic energy was released into the fluid by creating a deficit of tensile stress situated at the center of the computational domain in a small region given by $2\pi +A\ge \overline{x}\ge 2\pi -A$ and $\pi /2+A\ge \overline{z}\ge \pi /2-A$. Here, the non-dimensional $x$ and $z$ coordinates are given by $\overline{x}=x/l_y$ and $\overline{z}=z/l_y$, where $A=a/l_y=0.25$. As expected, this energy release creates two columnar vortex pairs with only vertical vorticity, which travel in opposite directions. Corresponding to the case shown in Figure 1, the space–time ($x-t$) coordinates of the maximum vertical vorticity of the left-traveling vortex pair is shown in Figure 2A. We determined that lateral ($z$) motion of the pair is negligible, indicating that the vortex pair travels almost entirely in the x-direction. We note that the vortex path shown in Figure 2A and a blow-up in Figure 2B exhibit two regions: a period of expansion, followed by one of translation. During expansion, the position of the maximum vorticity remains fixed in space, whereas during translation, its position changes.

For each numerical simulation performed in this work, we performed a linear curve fit of the $x-t$ path of the vorticity maximum during the translation period. In each case, the coefficient of determination ($R_{cd}^2$) fell in the range 0.986–0.999, indicating that a linear model is an excellent approximation for the vortex paths. We therefore use the slope, $dx/dt$, of the linear curve fit as the definition of the vortex speed in all simulations. Figure 2A shows an example of such a curve fit.

6. Linearized Wave Equation and the Undamped Solution

6.1. Linearized Wave Equation

While the results of the DNS simulations shown in Section 5 should be sufficient to verify the wave-like behavior of the vortices under consideration, it is useful to obtain further insight by examining the solutions of the linearized wave equation. In fact, it is shown that these simplified models give reasonable correspondence to the full simulations under conditions for which linearity is well approximated, and polymer relaxation times are large. In these models, we assume that the wave speed is given by the results of Section 3.

Consistent with the idea of using linearized model problems to gain further understanding of the results obtained from the DNS simulations, we consider a simplified version of Equation (21) given by

$$\ddot{\varphi }-C^2 {\partial }_1^2 \varphi -{\nu }_0\beta \left({\partial }_1^2\dot{\varphi }+{\partial }_3^2 \dot{\varphi }\right)=0,$$

(25)

where for simplicity, the scalar field, $\varphi$, has been substituted for ${\omega }_2$. This describes a field that propagates in one direction, $x_1$, which is entirely justified by the results obtained from the full equations of motion shown in Figure 2. The inclusion of viscous damping in two ($x_1,x_3)$ directions is motivated by the fact that the vortices observed in the simulations shown in Figure 1 are themselves two dimensional and should be expected to diffuse in the horizontal ($x_1-x_3$) plane. We excluded the term $\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right. {\dot{\omega }}_m$ in Equation (25) since we are interested in the situation with large polymer relaxation times, and we found in the cases of interest that this term has only a small effect on the decay of the vortex wave magnitude. The waves are assumed to propagate in an effectively infinite medium so no boundary conditions, except for radiation conditions, are required. We further note that damped wave equations have been investigated in the context of acoustics [77,78].

6.2. Analytical Solution for Undamped Waves

A salient aspect of the results shown in Figure 2A,B is the existence of a period of expansion followed by one of translation. Here, we show that this is entirely consistent with the solution of the undamped wave equation (Equation (25) without the damping terms) given by

$$\frac{{\partial }^2\varphi }{\partial x^2}-\frac{1}{C^2}\frac{{\partial }^2\varphi }{\partial t^2}=-\frac{Q}{C^2}\left\{\delta \left(x-a\right)-\delta \left(x+a\right)\right\}\delta \left(t\right).$$

(26)

In this inhomogeneous form of the wave equation, the source term on the right-hand side represents the initial conditions: the impulsive source is quiescent before being activated at time t = 0. The initial conditions for the model problem are that the initial field be zero, since the fluid is initially at rest, and that its time rate of change should be obtained from Equation (24): $\varphi \left(t=0\right)=0$ and

$${\left.\frac{\partial \varphi }{\partial t}\right|}_{t=0}=Q \left\{\delta \left(x-a\right)-\delta \left(x+a\right)\right\},$$

(27)

where Q represents the amplitude of the disturbance. The delta functions appearing in Equation (27) represent a model for the sharp gradients in the stress field, as described in Section 4, which result in the impulsive forces discussed in earlier work (see Figure 1 of [1]). The source strength, $Q$, in Equation (26) can be thought of as the amplitude of a force per unit mass whose spatial gradients give rise to vorticity.

The solution for the vorticity, ϕ, may be found by applying two Fourier transforms, one temporal and the other spatial, to both sides of Equation (26). After applying the appropriate inverse transforms, this procedure leads to the causal expression:

$$\varphi \left(x,t\right)=\frac{Q}{2\pi C}u\left(t\right){{\displaystyle \int }}_{-\infty }^{\infty }\frac{1}{p}\left[\cos p\left(x-a\right)-\cos p\left(x+a\right)\right]\sin \left(pCt\right)dp,$$

(28)

where u(t) is the Heaviside unit step function. Bearing in mind the identity

$${{\displaystyle \int }}_{-\infty }^{\infty }\cos \left(bs\right)ds=2\pi \delta \left(b\right),$$

(29)

it is evident that Equation (28) is consistent with the initial condition in Equation (27).

From an elementary identity, the products of the trigonometric functions in the integrands of Equation (28) may be expressed as the sum of two sine functions:

$$\cos p\left(x\pm a\right)\sin pCt=\frac{1}{2}\left[\sin p\left(x\pm a+Ct\right)-\sin p\left(x\pm a-Ct\right)\right],$$

(30)

and the integrals themselves then take the form

$${{\displaystyle \int }}_{-\infty }^{\infty }\frac{\sin pX}{p}dp=\pi \mathrm{sgn}\left(X\right),$$

(31)

where sgn(X) is the signum function, with values of +1 and −1, respectively, for X > 0 and X < 0. It follows that

$$\varphi \left(x,t\right)=\frac{Q}{4C}u\left(t\right)\left[\mathrm{sgn}\left(x-a+Ct\right)-\mathrm{sgn}\left(x-a-Ct\right)-\mathrm{sgn}\left(x+a+Ct\right)+\mathrm{sgn}\left(x+a-Ct\right)\right].$$

(32)

A schematic representation of this solution is given in Figure 3. As indicated in Figure 3B, at times such that$t\ll a/C$, the field $\varphi$ appears in the vicinity of $x=-a$ and $x=a$ as two spatially narrow boxcar functions, which are designated as $\alpha$and $\beta$, respectively. It is important to note in Figure 3B that the left and right sides of each boxcar travel in opposite directions with speed C, which results in spatially expanding fields, not translation. At time $t=a/C$ shown in Figure 3C, the fields have expanded to the maximum extent, and finally in Figure 3D, for t $>a/C$, the fields $\alpha$and $\beta$ propagate with a speed C to the left and right, respectively, since the sides of the boxcars propagate in the same direction. We designate the time separating expansion and translation as $T=a/C$. The existence of a time period of wave expansion followed by a period of wave translation agrees qualitatively with the results of Figure 2A,B. We should point out that the undamped solution given here shows that the vortices travel with constant amplitudes. However, in the numerical simulations, the viscosity is not zero, and this naturally has a smoothing effect that results in a peak in the wave amplitude. It is the space–time path of this peak that is shown in Figure 2A,B. The effects of viscosity, as predicted by the linearized theory, are described below.

7. Viscous Effects

Here, we consider the effects of viscosity on the evolution of vortex waves. Recall that a good approximation for the wave speed is $\mathrm{C}=\sqrt{{\mathsf{\alpha }\mathrm{fC}}_{11}^0}$, in which $\mathsf{\alpha }={\mathsf{\nu }}_0\left(1-\mathsf{\beta }\right)/\mathsf{\lambda }$. Thus, the wave speed itself is viscosity dependent. In addition, the viscosity of the fluids typically used in microfluidics [3] are high, resulting in low Reynolds numbers. In this section, we first present results from the numerical simulation for the evolution of the vorticity magnitude, followed by the development of analytical solutions of the linearized wave equation with damping in one and two dimensions.

7.1. Temporal Evolution of the Vorticity Magnitude from Numerical Simulations

The temporal evolution of the magnitude of the maximum vertical vorticity following a typical vortex wave is shown in Figure 4. These results were obtained from the numerical simulation described in Figure 1. Since the fluid is modeled as a solution having viscosity ${\nu }_0$, it is expected that the wave energy will decay after being released. This is in fact what is observed in Figure 4A, which shows a rapid rise in vorticity followed by decay. In Figure 4B, the time taken for the vorticity to reach a maximum is compared to the transition time, $T=a/C$. This shows that the maximum vorticity appears at a time somewhat before the transition time, which indicates the growth of wave energy lies entirely within the time scale T.

7.2. One-Dimensional Analytical Solution of the Linearized Wave Equation with Viscosity

To gain further insight into the results of the numerical simulations discussed above, an analytical solution of Equation (25) is now developed in which the effect of viscous damping on the evolution of the vortices is taken into account. Following the formalism of the undamped case in Equation (26), the one-dimensional version of Equation (25) with damping included may be written in the inhomogeneous form

$$\frac{{\partial }^2\varphi }{\partial x^2}-\frac{1}{C^2}\frac{{\partial }^2\varphi }{\partial t^2}+\chi \frac{{\partial }^3\varphi }{\partial t\partial x^2}=-\frac{Q}{C^2}\left[\delta \left(x-a\right)-\delta \left(x+a\right)\right]\delta \left(t\right),$$

(33)

where, on the left, the coefficient of the third-order derivative, representing damping, is

$$\chi =\frac{{\nu }_0\beta }{C^2}$$

(34)

It is important to note that the damping coefficient, χ, is in general non-zero, thus giving rise to a smoothing of the vortex field, but χ is itself independent of the viscosity as, according to Equation (23), the vortex speed, C, scales as the square root of the viscosity, from which it follows that ${\nu }_0$ cancels out of Equation (34). This situation is the reverse of that associated with acoustic propagation in a viscous fluid: Stokes’ equation [77] for the acoustic field has exactly the same structure as that on the left of Equation (33), but the acoustic analogs of C and χ are, respectively, independent of and proportional to the viscosity. According to Equation (33), even though χ is invariant with ${\nu }_0$, the viscosity will affect the travel time and the shape of a vortex, since C² in the second term on the left scales with ${\nu }_0$.

As with the undamped case, the solution for the vortex field may be obtained by applying a pair of Fourier transforms to Equation (33), one temporal and one spatial, as detailed in Appendix C. This procedure leads to a wave number integral for the field:

$$\varphi \left(x,t\right)=-i\frac{Q}{\pi }{C}^{2}u\left(t\right){{\displaystyle \int }}_{-\infty }^{\infty }\sin \left(pa\right)e^{-p^2\chi C^{2}t/2}\frac{\sin \left(Rt\right)}{R}{e}^{ipx}dp,$$

(35)

where u(t) is the Heaviside unit step function and

$$R=\frac{1}{2}\sqrt{4p^2{C}^2-{\chi }^2{C}^4{p}^4}.$$

(36)

Bearing in mind the delta function identity in Equation (29), it is readily shown that, at the origin of time, t = 0, the time derivative of the field in Equation (35) is identical to the second of the initial conditions in Equation (27). In fact, everywhere in the medium, apart from x = ±a, the vortex field itself in Equation (35) and all of its time derivatives are identically zero at t = 0; that is to say, the field is maximally flat, or infinitely flat, at the instant the source is activated. Such behavior is also exhibited by Stokes’ equation for acoustic propagation in a viscous fluid [77] and by the time-dependent diffusion equation [77]. Thus, in all three cases, the field satisfies causality in the strict sense: it is zero at negative times with no instantaneous arrivals anywhere in the fluid medium surrounding the source.

The function R in Equation (36) is real when $\left|p\right| <q$ and imaginary when $\left|p\right| >q$, where

$$q=\frac{2}{\chi C}.$$

(37)

For all practical values of χ, the contribution to the integral in Equation (35) from the imaginary components of R is negligible, and for R real, an excellent approximation is

$$R \approx \left|p\right|C.$$

(38)

Under these conditions, the integral in Equation (35) may be approximated in terms of the error function, erf(.), as shown in Appendix C:

$$\begin{gathered} \overline{\varphi }\approx \frac{1}{2}sgn\left(1-\frac{2\overline{t}}{qa}+\overline{x}\right)erf\left(\frac{qa}{2\sqrt{2\overline{t}}}\left|1-\frac{2\overline{t}}{qa}+\overline{x}\right|\right) \\ -\frac{1}{2}sgn\left(1-\frac{2\overline{t}}{qa}-\overline{x}\right)erf\left(\frac{qa}{2\sqrt{2\overline{t}}}\left|1-\frac{2\overline{t}}{qa}-\overline{x}\right|\right) \\ -\frac{1}{2}sgn\left(1+\frac{2\overline{t}}{qa}+\overline{x}\right)erf\left(\frac{qa}{2\sqrt{2\overline{t}}}\left|1+\frac{2\overline{t}}{qa}+\overline{x}\right|\right) \\ +\frac{1}{2}sgn\left(1+\frac{2\overline{t}}{qa}-\overline{x}\right)erf\left(\frac{qa}{2\sqrt{2\overline{t}}}\left|1+\frac{2\overline{t}}{qa}-\overline{x}\right|\right), \end{gathered}$$

(39)

where sgn(.) is the signum function taking values of +1 and −1, respectively, for positive and negative arguments. A simple normalization scheme has been introduced in Equation (39), whereby

$$\overline{t}=\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$\chi $}\right.\mathrm{and}\overline{x}=\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$a$}\right..$$

(40)

The factor of ½ in each of the four terms in Equation (39) ensures that, in the absence of damping, when χ = 0, the peak value of the normalized vortex field is $\overline{\varphi }=1$. It is worth noting that when χ = 0, the error functions in Equation (39) are all unity, and the field reduces to precisely the same rectangular boxcar form as that of the undamped solution in Equation (32). The normalization scheme in Equation (40) can also be applied to the exact integral solution in Equation (35), in which case the normalized vorticity field becomes

$$\begin{gathered} \overline{\varphi }=\frac{4}{\pi }{{\displaystyle \int }}_0^1\cos \left[\overline{p}qa\left(\overline{x}-1\right)\right]\frac{\sin \left(\overline{R} \overline{t}\right)}{\overline{R}}{e}^{-2{\overline{p}}^2\overline{t}}d\overline{p}+\frac{4}{\pi }{{\displaystyle \int }}_1^{\infty }\cos \left[\overline{p}qa\left(\overline{x}-1\right)\right]\frac{\sin \mathrm{h}\left(\mathrm{S} \overline{t}\right)}{\overline{S}}{e}^{-2{\overline{p}}^2\overline{t}}d\overline{p} \\ -\frac{4}{\pi }{{\displaystyle \int }}_0^1\cos \left[\overline{p}qa\left(\overline{x}+1\right)\right]\frac{\sin \left(\overline{R} \overline{t}\right)}{\overline{R}}{e}^{-2{\overline{p}}^2\overline{t}}d\overline{p}-\frac{4}{\pi }{{\displaystyle \int }}_1^{\infty }\cos \left[\overline{p}qa\left(\overline{x}+1\right)\right]\frac{\sin \mathrm{h}\left(\mathrm{S} \overline{t}\right)}{\overline{S}}{e}^{-2{\overline{p}}^2\overline{t}}d\overline{p}, \end{gathered}$$

(41)

where

$$\overline{R}=2\sqrt{{\overline{p}}^2-{\overline{p}}^4},\overline{S}=\sqrt{{\overline{p}}^4-{\overline{p}}^2}\mathrm{and}\overline{p}=\frac{p}{q}.$$

(42)

An advantage of the normalization in Equations (39) and (41) is that the wave speed C in which the viscosity ${\nu }_0$ is embedded, the damping coefficient $\chi$, and the source positions at |x| = a, all collapse into the single parameter, $a=\frac{2a}{\chi C}$, which, through the presence of C, varies as the inverse square root of the viscosity. Bearing in mind that the normalizing terms χ and a in the denominators of Equation (40) are independent of ν₀, it is evident that the effects of viscosity on the normalized vortex field in Equations (39) and (40) are represented solely by the dimensionless parameter qa. Therefore, with a fixed receiver position, $\overline{x}$, a family of curves for $\overline{\varphi }$ as a function of $\overline{t}$ may be generated in which each curve corresponds to a particular value of qa, with lower values of qa representing higher viscosities. Two such families of curves, for $\overline{x}=0.5$ and $\overline{x}=2$, are shown in Figure 5 (N.B. the logarithmic time scale).

These curves were computed by numerical evaluation of the integrals in Equation (40), but the error function approximation in Equation (39) could have been used since it returns almost identical results for viscosities represented by the condition qa ≥ 10. For smaller values of qa, corresponding to inordinately high viscosities, the error function approximation in Equation (39) becomes increasingly inaccurate, and instead, the exact integral formulation in Equation (41) is recommended. Three effects of increasing the viscosity are illustrated by the vorticity fields shown in Figure 5: the travel time is progressively reduced, consistent with the scaling of the wave speed as the square root of the viscosity; the rectangular boxcar shape characteristic of low viscosities becomes more rounded; and the maximum level of the normalized vortex field is reduced.

7.3. Two-Dimensional Analytical Solution of the Linearized Wave Equation with Viscosity

It was found through comparison of the simulations with the analytical model described above that wave damping in one dimension gives wave amplitudes that decay more slowly than indicated by the numerical simulations. To gain further insight into the viscous decay of the vortex, the wave equation in Equation (25), may be written in inhomogeneous form as

$$\frac{{\partial }^2\varphi }{\partial x^2}-\frac{1}{C^2}\frac{{\partial }^2\varphi }{\partial t^2}+\chi \frac{\partial }{\partial t}\left\{\frac{{\partial }^2\varphi }{\partial x^2}+\frac{{\partial }^2\varphi }{\partial z^2}\right\}=-\frac{Q}{C^2}\left[\delta \left(x-a\right)-\delta \left(x+a\right)\right]\delta \left(z\right)\delta \left(t\right),$$

(43)

where

$$\chi =\frac{{\nu }_0\beta }{C^2}.$$

(44)

Note that damping terms in $x$ and $z$ are added (third term on the left-hand side of Equation (43)). The solution to Equation (43) is given in Appendix D.

Here, we are particularly interested in the rate of decay of the vorticity, which is evident in Figure 4 for $t>\frac{a}{C}=T$. It is reasonable to approximate this decay as an exponential of the form $e^{-\sigma t}$ to model the evolution of both the vorticity obtained from the numerical simulations and the analytical solution, Equation (A25), which has been evaluated numerically. The results for the numerical simulations shown in Figure 4 and the model (Equation (43)) are $\overline{\sigma }=0.766$and 0.732 where $\overline{\sigma }=\sigma a^2/{\nu }_0$, where the coefficients of determination ($R_{cd}^2$) for the exponential model were $0.99$ and $0.98$, respectively. The satisfactory agreement for the decay rates indicates that the decay in the vorticity of the vortex wave can be accounted for reasonably well by viscous diffusion in two dimensions. It is also notable that the decay time, ${\tau }_d$, for the vortex wave is ${\tau }_d~O\left(a^2/{\nu }_0\right)$, as expected from dimensional considerations, since the size of the vortex is on the order of $a$.

8. Vortex Wave Speed

Here, numerical simulations are used to determine the effects of wave amplitude, the initial elastic stress in the fluid, and the maximum polymer extension length on the speed of vortex waves. The results below show excellent agreement between the linearized theory discussed in Section 3 and provide strong evidence for the existence of vortex waves.

8.1. Effect of Wave Amplitude on Wave Speed

The full equations of motion (1)–(6) contain nonlinearities, such as advection, vortex stretching and tilting, and polymer stretching, which are fully represented in all numerical simulations presented in this work. The effects of these nonlinearities on wave motion can be important for waves of high amplitude [70]. For example, acoustic waves can be characterized by the ratio $\Delta p/p_0$, where $\Delta p$ is the amplitude of the wave and $p_0$ is the ambient atmospheric pressure. When an acoustic wave passes a given location, the perturbation in the pressure, $\Delta p$, is normally observed by acoustic sensors. When $\Delta p/p_0$ << 1, acoustic waves have a well-known speed given by $c_0=\sqrt{\gamma p_0/{\rho }_0}$, where $\gamma$ is the ratio of specific heats and ${\rho }_0$ is the ambient air density. However, acoustic waves of high amplitude (e.g., shock waves) can have speeds higher than $c_0$. Moreover, high amplitude nonlinear waves can exhibit other effects, such as wave steepening, and dispersion (e.g., ocean waves).

It is therefore of interest to determine the effects of wave amplitude on the propagation of vortex waves. This was achieved by performing numerical simulations in which the fluid properties were fixed and using the linear spring model, $f\left(R\right)=1$, while varying the amplitude parameter $N={\epsilon }_0/C_{11}^0$, the ratio of the initial stress deficit to the background stress, by more than an order of magnitude. Here, $N$ can thought of as analogous to $\Delta p/p_0$ for acoustic waves. Here, we define (see Section 3) the theoretical wave speed by$C=\sqrt{\alpha f{C}_{11}^0+\raisebox{1ex}{$f$}\!\left/ \!\raisebox{-1ex}{$\lambda $}\right.{\nu }_0\beta }$.

The results shown in Figure 6 indicate that the wave speed is virtually unaffected by the wave amplitude. In addition, the difference between the wave speeds obtained from the simulations shown in Figure 6 and the theoretical linear wave speed was <1.5% in all cases. This indicates that, over a significant range of wave amplitude, a linear wave model is a good approximation for the observed dynamics.

8.2. Effect of the Initial Elastic Stress on Wave Speed

The dependence of wave speed on $C_{11}^0$ for the linear spring model$f\left(R\right)=1$ is shown in Figure 7. In these simulations, all fluid properties were fixed and $N={10}^{-2}$, thus ensuring linearity. These results show clearly that the wave speeds predicted by the linearized model are in excellent agreement with the numerical simulations. In fact, the difference between the wave speeds obtained from the simulations shown in Figure 7 and the theoretical linear wave speeds was <1.1% in all cases. As further evidence for the accuracy of the linearized theory of vortex waves, we show in Figure 2C the relation between the transition time, $T=a/C$, and $C_{11}^0$ for both simulations and theory. The agreement is again quite reasonable and further justifies the model given in Section 6.2. Furthermore, it indicates that for the kind of initial conditions we imposed on the flow, a reasonable estimate of the vortex wave speed can be obtained from T and the length scale $a$.

8.3. Effect of the Maximum Polymer Extensional Length on Wave Speed

It is also of interest to determine the effect of a nonlinear spring on vortex wave speed by allowing the spring constant in the polymer model to be determined by the Peterlin function $f\left(R\right)=\left(L^2-3\right)/\left(L^2-R^2\right)$. Here, we note that $f\to 1$ as the maximal allowable polymer extensional length ($L$) becomes large compared to $R^2=\mathrm{tr}\left(C\right)$. In this limit, it is expected that the wave speed should approach the linear theory limit. To test this, wave speeds were determined as$L$was varied over two orders of magnitude, with all other fluid and polymer properties fixed, and with $R^2~2\times {10}^3$ during the course of the simulations. The results shown in Figure 8 indicate that at the largest value of $L$, wave speeds approach nearly the theoretical speed for linear waves. However, as $L$ decreases, the Peterlin function increases, corresponding to an increasingly stiff spring. The effect of this is to increase vortex wave speed, an expected result that is clearly indicated in Figure 8. It should also be noted that in every case, the vortex wave speed is greater than the linear theory wave speed for these nonlinear springs.

9. Summary and Discussion

Recent work [1] has shown that the release of elastic energy in a viscoelastic fluid can produce coherent vorticity, which is generated by torque-producing elastic stress gradients. However, in that work, the kinematics of the motion of the coherent vortical structures was not fully explored. In this work, we show that the release of elastic energy generates vorticity that propagates as a wave, whose speed is governed by the initial stress field in the fluid. A linearized version of the equations of motion for an incompressible fluid, which includes the FENE-P model for polymer dynamics, shows that waves of vorticity should be generated upon release of stored elastic energy. For large polymer relaxation times and for a linear spring model ($f=1$), the vortex wave speed is shown to be $C\propto \sqrt{C_{11}^0}$, where $C_{11}^0$ is the initial longitudinal polymer conformation, proportional to the initial tension in the fluid. Furthermore, the theory shows that the wave should be affected by the fluid viscosity. Insight was obtained by using an undamped model for the case in which energy is released in a spatially symmetric manner. This shows that the temporal evolution of the wave takes place in two parts: (1) a period of expansion in which the field grows in spatial extent but does not propagate, followed by (2) a field which propagates at speed $C$. The period of expansion is shown to take place during a time $=a/C$, where $a$ is the spatial location at which energy is released, and also represents the length scale or size of the wave. In addition, an analytical solution to the linearized equations with viscous damping was used to determine a viscous decay time scale.

Analogous to physical experiments, a series of direct numerical simulations (DNS) were performed for a range of parameters that could be compared with the theory. For low amplitude waves that are governed by a linear spring model, the DNS gave results very much in accord with the linearized theory: (1) wave speeds obtained from DNS were within 1.5% of the theory, and (2) the time scale associated with the period of wave expansion matched DNS results. In addition, an analytical solution of the wave equation with viscous damping was used to determine a viscous decay time scale. This time scale was in good agreement with DNS results.

An additional motivation for undertaking this work is associated with the problem of promoting mixing in low Reynolds flows, such as those associated with microfluidics. As such, coherent vortex motions may be useful for the enhancement of transport in low Reynolds number, high Peclet number flows in micro-devices. The possibility of experimentally verifying the phenomena described in this work is also being pursued. For example, recent experiments [79] in which an extensional flow of a dilute polymer solution using a convergent–divergent flow field revealed chaotic flow behavior. If stored elastic energy in such a flow could be released in a controlled manner, then fluid motions similar to the ones observed in our simulations should be generated. It is also interesting to observe that vortex waves can easily be made to propagate in any desired direction. For example, if stored elastic energy placed in $C_{22}$ is suddenly released, we should expect the resultant vortex waves to propagate in the vertical direction, perpendicular to walls. Future work should also consider the effects of an initially asymmetric stress distribution, as well as the effects of strong, finite amplitude waves.