Numerical Study on Pool Boiling of Hybrid Nanofluids Using RPI Model
Abstract
:1. Introduction
2. Literature Overview
3. The Aim of This Work
4. Theoretical Formulation and Numerical Simulation
4.1. Governing Equations
4.2. Phase Interaction (Interfacial Exchange)
4.3. Heat Flux Partitioning Boiling Submodel
4.4. Thermophysical Properties
4.5. Domain Description
4.6. Assumptions
- The problem under consideration is the transient and turbulent flow due to bubble formation in the nucleate pool boiling regime.
- As a result of molecular mixing of the low concentration of hybrid nanoparticles and water, the hydrodynamic behavior of the hybrid nanofluids would be similar to that of the single-phase nanofluid. Therefore, a single-phase model is considered in this study.
- Under the specified operating temperature and pressure, the thermophysical characteristics of water and vapor phases are assumed to be constant.
- The operating pressure of the chamber is controlled to be the same as the atmospheric pressure condition, then the pressure is .
- Due to the low volume fraction employed in this analysis, the surface tension parameter of hybrid nanofluids is presumed to be the same as that of water.
- The temperature of the DI water inside the chamber is the saturation temperature.
- Due to the high density ratio between the water and vapor phases, the vapor phase is also believed to be quite light to take the nanoparticles within. Therefore, it is considered that the stable nanoparticles do not affect the thermal properties of the vapor phase.
- For this simulation, a time interval size of (0.001 s) is used. Moreover, following a trial-and-error strategy to ensure that the solution is convergence at each time step, the maximum number of iterations per time step was adjusted to 100.
4.7. Numerical Methods and Boundary Conditions
4.8. Grid Test and Validation
5. Results and Discussion
5.1. Bubble Waiting Time Coefficient Correlations
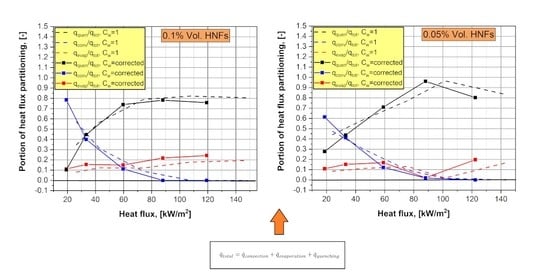
5.2. Portions of the RPI Model
5.3. Contours of Vapor Volume Fraction
5.4. Vectors of Vapor Velocity
5.5. Velocity of Water Streamlines
6. Conclusions and Future Direction
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| DI | Deionized water |
| RPI | Rensselaer Polytechnic Institute |
| BWTC | Coefficient of buuble waiting time |
| PBHT | Pool boiling heat transfer |
| PBHTC | Pool boiling heat transfer coefficient |
| HNFs | Hybrid nanofluids |
| HTC | Heat transfer coefficient |
| FVM | Finite volume method |
| [kW m−2] | Total heat flux |
| [kW m−2] | Quenching heat flux |
| [kW m−2] | Evaporative heat flux |
| [kW m−2] | Convection heat flux |
| P [kPa] | Pressure system |
| [m] | Diameter of bubble |
| [Hz] | Frecuency of bubble |
| Density of nucleation site | |
| Twall [K] | Wall temperature |
| Twater [K] | Water temperature |
| Tsat [K] | Saturation temperature |
| [K] | Superheat temperature |
| [kW m−2 K] | Interface heat transfer coefficient |
| Interphase momentum transfer term | |
| [J kg−1 K−1] | Water-phase specific heat |
| [pa s] | Water-phase viscosity |
| [W m−1 K−1] | Water-phase thermal conductivity |
| [%] | Volume friction |
| [degree] | Contact angle for nanoporous surface |
| [degree] | Contact angle for clean surface |
| [−] | Wettability improvement parameter |
| [m2] | Convection area friction |
| [m2] | Quenching area friction |
| [µm] | Average surface roughness |
| Surafce interaction parameter | |
| Nu [−] | Nusslte number |
| Re [−] | Reynolds number |
References
- Mahian, O.; Kolsi, L.; Estellé, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; Wongwises, S.; et al. Recent Advances in Modeling and Simulation of Nanofluid Flows-Part I: Fundamental and Theory. Phys. Rep. 2018, 790, 1–48. [Google Scholar] [CrossRef]
- Said, Z.; Sundar, L.S.; Tiwari, A.K.; Ali, H.M.; Sheikholeslami, M.; Bellos, E.; Babar, H. Recent advances on the fundamental physical phenomena behind stability, dynamic motion, thermophysical properties, heat transport, applications, and challenges of nanofluids. Phys. Rep. 2021, 946, 1–94. [Google Scholar] [CrossRef]
- Kamel, M.S.; Al-Oran, O.; Lezsovits, F. Thermal Conductivity of Al2O3 and CeO2 Nanoparticles and Their Hybrid Based Water Nanofluids: An Experimental Study. Period. Polytech. Chem. Eng. Therm. 2021, 65, 50–60. [Google Scholar] [CrossRef]
- Souayeh, B.; Hammami, F.; Hdhiri, N.; Alam, M.W.; Yasin, E.; Abuzir, A. Simulation of natural convective heat transfer and entropy generation of nanoparticles around two spheres in horizontal arrangement. Alex. Eng. J. 2021, 60, 2583–2605. [Google Scholar] [CrossRef]
- Liang, G.; Mudawar, I. Review of pool boiling enhancement by surface modification. Int. J. Heat Mass Transf. 2019, 128, 892–933. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. In Developments and Applications of Non-Newtonian Flows; Siginer, D.A., Wang, H.P., Eds.; Argonne National Lab. (ANL): Argonne, IL, USA, 1995; Volume 66, pp. 281–285. [Google Scholar]
- Kamel, M.S.; Lezsovits, F.; Hussein, A.M.; Mahian, O.; Wongwises, S. Latest developments in boiling critical heat flux using nanofluids: A concise review. Int. Commun. Heat Mass Transf. 2018, 98, 59–66. [Google Scholar] [CrossRef]
- Kamel, M. Saad boiling heat transfer of nanofluids: A review of recent studies. Therm. Sci. 2019, 23, 109–124. [Google Scholar] [CrossRef] [Green Version]
- Kamel, M.S.; Lezsovits, F.; Hussein, A.K. Experimental studies of flow boiling heat transfer by using nanofluids. J. Therm. Anal. Calorim. 2019, 138, 4019–4043. [Google Scholar] [CrossRef] [Green Version]
- Sajid, M.U.; Ali, H.M. Thermal conductivity of hybrid nanofluids: A critical review. Int. J. Heat Mass Transf. 2018, 126, 211–234. [Google Scholar] [CrossRef]
- Babar, H.; Sajid, M.; Ali, H. Viscosity of hybrid nanofluids: A critical review. Therm. Sci. 2019, 23, 1713–1754. [Google Scholar] [CrossRef] [Green Version]
- Wei, B.; Zou, C.; Yuan, X.; Li, X. Thermo-physical property evaluation of diathermic oil based hybrid nanofluids for heat transfer applications. Int. J. Heat Mass Transf. 2017, 107, 281–287. [Google Scholar] [CrossRef]
- Cieśliński, J.T.; Kaczmarczyk, T.Z. Pool boiling of water-Al2O3 and water-cu nanofluids outside porous coated tubes. Heat Transf. Eng. 2015, 36, 553–563. [Google Scholar] [CrossRef]
- Sarafraz, M.M.; Pourmehran, O.; Yang, B.; Arjomandi, M.; Ellahi, R. Pool boiling heat transfer characteristics of iron oxide nano-suspension under constant magnetic field. Int. J. Therm. Sci. 2020, 147, 106131. [Google Scholar] [CrossRef]
- Manetti, L.L.; Cardoso, E.M.; Nascimento, F. Do Nanofluid Pool Boiling: The Effect of Time, Concentration and Heat Flux on the Heat Transfer. In Proceedings of the 9th World Conference on Experimental Heat Transfer, Fluid Mechanics and Thermodynamics, Iguazu Falls, Brazil, 11–15 June 2017. [Google Scholar]
- Ali, H.M.; Generous, M.M.; Ahmad, F.; Irfan, M. Experimental investigation of nucleate pool boiling heat transfer enhancement of TiO2-water based nanofluids. Appl. Therm. Eng. 2017, 113, 1146–1151. [Google Scholar] [CrossRef]
- Kamel, M.S.; Lezsovits, F. Enhancement of pool boiling heat transfer performance using dilute cerium oxide/water nanofluid: An experimental investigation. Int. Commun. Heat Mass Transf. 2020, 114, 104587. [Google Scholar] [CrossRef]
- Kamel, M.S.; Lezsovits, F.; Ali Abdollahi, M.I. Amelioration of pool boiling thermal performance in case of using a new hybrid nanofluid. Case Stud. Therm. Eng. 2021, 24, 100872. [Google Scholar] [CrossRef]
- Kamel, M.S.; Lezsovits, F. Experimental Investigation on Pool Boiling Heat Transfer Performance Using Tungsten Oxide WO3 Nanomaterial-Based Water Nanofluids. Materials 2020, 13, 1922. [Google Scholar] [CrossRef]
- Mortezazadeh, R.; Aminfar, H.; Mohammadpourfard, M. Eulerian–Eulerian simulation of non-uniform magnetic field effects on the ferrofluid nucleate pool boiling. J. Eng. Thermophys. 2017, 26, 580–597. [Google Scholar] [CrossRef]
- Aminfar, H.; Mohammadpourfard, M.; Sahraro, M. Numerical simulation of nucleate pool boiling on the horizontal surface for nano-fluid using wall heat flux partitioning method. Comput. Fluids 2012, 66, 29–38. [Google Scholar] [CrossRef]
- Niknam, P.H.; Haghighi, M.; Kasiri, N.; Khanof, M.H. Numerical study of low concentration nanofluids pool boiling, investigating of boiling parameters introducing nucleation site density ratio. Heat Mass Transf. Waerme-Stoffuebertragung 2015, 51, 601–609. [Google Scholar] [CrossRef]
- Mahdavi, M.; Sharifpur, M.; Meyer, J.P. Exploration of nanofluid pool boiling and deposition on a horizontal cylinder in Eulerian and Lagrangian frames. Int. J. Heat Mass Transf. 2018, 125, 959–971. [Google Scholar] [CrossRef] [Green Version]
- Kamel, M.S.; Lezsovits, F. Predicting of Pool Boiling Heat Transfer From a Horizontal Heated Tube Using Two Fluids Multiphase Model. J. Adv. Res. Fluid Mech. Therm. Sci. 2020, 71, 38–55. [Google Scholar] [CrossRef]
- Kamel, M.S.; Al-agha, M.S.; Lezsovits, F.; Mahian, O. Simulation of pool boiling of nanofluids by using Eulerian multiphase model. J. Therm. Anal. Calorim. 2020, 142, 493–505. [Google Scholar] [CrossRef] [Green Version]
- Mousavi, F.; Adibi, P. Numerical investigation of surface roughness effect on pool boiling heat transfer of Al2O3/water nanofluid. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 1535–1549. [Google Scholar] [CrossRef]
- Zaboli, S.; Alimoradi, H.; Shams, M. Numerical investigation on improvement in pool boiling heat transfer characteristics using different nanofluid concentrations. J. Therm. Anal. Calorim. 2022, 1–18. [Google Scholar] [CrossRef]
- Shakir, H.; Abdul, H.M.; Jaafer, L.; Zivkovic, D. Pool boiling simulation of two nanofluids at multi concentrations in enclosure with different shapes of fins. Mater. Today Proc. 2022, 60, 2043–2063. [Google Scholar] [CrossRef]
- Mao, S.; Ji, W.; Chong, G.; Zhao, C.; Zhang, H. Numerical investigation on the nucleate pool boiling heat transfer of R134a outside the plain tube. Numer. Heat Transf. Part A Appl. 2019, 76, 889–908. [Google Scholar] [CrossRef]
- Salehi, H.; Hormozi, F. Numerical study of silica-water based nanofluid nucleate pool boiling by two-phase Eulerian scheme. Heat Mass Transf. 2018, 54, 773–784. [Google Scholar] [CrossRef]
- Kamel, M.S. Numerical and Experimental Investigation on Pool Boiling Heat Transfer Performance Using Nanofluids. Doctoral Dissertation, Budapest University of Technology and Economic, Budapest, Hungary, 2020. [Google Scholar]
- Noori Rahim Abadi, S.M.A.; Ahmadpour, A.; Meyer, J.P. Numerical simulation of pool boiling on smooth, vertically aligned tandem tubes. Int. J. Therm. Sci. 2018, 132, 628–644. [Google Scholar] [CrossRef] [Green Version]
- Ranz, W.E.; Marshall, W.R. Vaporation from Drops, Part I. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Troshko, A.A.; Hassan, Y.A. A two-equation turbulence model of turbulent bubbly flows. Int. J. Multiph. Flow 2001, 27, 1965–2000. [Google Scholar] [CrossRef]
- Drew, D.A.; Lahey, R.T.I. Particulate Two-Phase Flow; Roco, M.S., Ed.; Butterworth-Heinemann Series in Chemical Engineering; Butterworth-Heinemann: Boston, MA, USA, 1993. [Google Scholar]
- Ishii, M. Two-fluid model for two-phase flow. In 2nd International Workshop on Two-phase Flow Fundamentals; Rensselaer Polytechnic Institute: Troy, NY, USA, 1979. [Google Scholar]
- Lopez de Bertodano, M. Turbulent Bubbly Flow in a Triangular Duct; Rensselaer Polytechnic Institute: Troy, NY, USA, 1991. [Google Scholar]
- Tomiyama, A. Struggle with computational bubble dynamics. In Proceedings of the Third International Conference on Multiphase Flow, Lyon, France, 8–12 June 1998. [Google Scholar]
- Antal, S.P.; Lahey, R.T.; Flaherty, J.E. Analysis of phase distribution in fully developed laminar bubbly two-phase flow. Int. J. Multiph. Flow 1991, 17, 635–652. [Google Scholar] [CrossRef]
- Kurul, N.; Podowski, M.Z. On the modeling of multidimensional effects in boiling channels. In Proceedings of the 27th National Heat Transfer Conference, Minneapolis, MN, USA, 28–31 July 1991. [Google Scholar]
- Kurul, N.; Podowski, M.Z. Multidimensional effects in forced convection subcooled boiling. In Proceedings of the Ninth International Heat Transfer Conference, Jerusalem, Israel, 19–24 August 1990. [Google Scholar]
- Lemmert, M.; Chawla, J.M. Influence of flow velocity on surface boiling heat transfer coefficient in Heat Transfer in Boiling. In Heat Transfer in Boiling; Hahne, E., Grigull, U., Eds.; Academic Press and Hemisphere: New York, NY, USA, 1977. [Google Scholar]
- Ganapathy, H.; Sajith, V. Semi-analytical model for pool boiling of nanofluids. Int. J. Heat Mass Transf. 2013, 57, 32–47. [Google Scholar] [CrossRef]
- Kocamustafaogullari, G.I. Foundation of the interracial area transport equation and its closure relations. Int. J. Heat Mass Transfer. 1995, 38, 481–493. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Y.; Tu, J. A parametric study of the heat flux partitioning model for nucleate boiling of nanofluids. Int. J. Therm. Sci. 2015, 98, 42–50. [Google Scholar] [CrossRef]
- Lemmon, E.W.; McLinden, M.O.; Friend, D.G. Thermophysical Properties of Fluid Systems, National Institute of Standard and Technology NIST Chemistry WebBook; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. [Google Scholar]
- Minea, A.A.; Moldoveanu, M.G. Overview of Hybrid Nano fl uids Development and Bene fi ts. J. Eng. Thermophys. 2018, 27, 507–514. [Google Scholar] [CrossRef]
- Oztop, H.F.; Abu-nada, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. Int. J. Heat Fluid Flow 2008, 29, 1326–1336. [Google Scholar] [CrossRef]












| Forces | Model [Ref.] | Formulation |
|---|---|---|
| Virtual mass forces | Explicit source term [35] | is the virtual mass constant, which is equal by default (0.5), and the term denotes the liquid-phase time derivative. |
| Drag force | Ishii [36] | is the drag coefficient and is achieved by choosing the minimum of and which are the coefficients of the viscous and distorted regimes, respectively. |
| Turbulent dispersion force | Lopez-de-bertodano [37] | is a user-modifiable constant that is set to 1, is the turbulent kinetic energy in the water phase. is the gradient of the vapor-phase volume fraction. |
| Lift force | Tomiyama [38] | is the lift coefficient is a modified Eotvos number that is defined as follows: are deformable bubbles and bubble diameter. |
| Wall lubrication force | Antal et al. [39] | are the wall lubrication coefficient and the normal unit pointing away from the wall. ; , are non-dimensional coefficients. |
| Property | DI Water [46] | Vapor [46] | Al2O3 [26] | MgO [47] | Hybrid (50:50) |
|---|---|---|---|---|---|
| Density | 958.35 | 0.59817 | 3490 | 3580 | 3535 |
| Specific heat | 4215.7 | 2080 | 451 | 874 | 662.5 |
| Thermal conductivity | 0.67909 | 0.02509 | 25 | 55 | 40 |
| Dynamic viscosity | 0.000281 | 0.0000122 | - | - | - |
| Surface tension | 0.0589 | - | - | - | - |
| Domain Structure | Working Fluids | Model/Submodel | Boundary Conditions (BCs) | Purpose of Simulation | Studied Parameters |
|---|---|---|---|---|---|
| 2-D square chamber with a horizontal copper heater as in the experimental work of [31] | Water–vapor two-phase flow Alumina/magnesium oxide hybrid nanofluid–vapor two-phase flow | Eulerian–Eulerian multiphase model/RPI boiling submodel | Validation Pool boiling heat transfer performance prediction | Pool boiling curve PBHTC Heat flux partitioning portions V-V-V * V-V-F ** W.S.V *** |
| Statistics and Parameters | DI Water | 0.05 Vol.% HNFs | 0.1 Vol.% HNFs |
|---|---|---|---|
| Number of points | 5 | 5 | 5 |
| Degrees of freedom | 2 | 2 | 2 |
| Residual sum of residual | 6.497 × 10−5 | 0.0077 | 0.0069 |
| R-square (COD) | 0.999 | 0.966 | 0.962 |
| Adj. R-square | 0.998 | 0.932 | 0.923 |
| Intercept value | −0.1499 | −0.4313 | 0.2757 |
| Intercept standard error | 0.0235 | 0.1955 | 0.1909 |
| B1 value | 0.0594 | 0.2058 | 0.1312 |
| B1 standard error | 0.0059 | 0.0605 | 0.0545 |
| B2 value | −8.797 × 10−4 | −0.0095 | −0.0046 |
| B2 standard error | 3.309 × 10−4 | 0.0041 | 0.0034 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamel, M.S.; Albdoor, A.K.; Nghaimesh, S.J.; Houshi, M.N. Numerical Study on Pool Boiling of Hybrid Nanofluids Using RPI Model. Fluids 2022, 7, 187. https://doi.org/10.3390/fluids7060187
Kamel MS, Albdoor AK, Nghaimesh SJ, Houshi MN. Numerical Study on Pool Boiling of Hybrid Nanofluids Using RPI Model. Fluids. 2022; 7(6):187. https://doi.org/10.3390/fluids7060187
Chicago/Turabian StyleKamel, Mohammed Saad, Ahmed K. Albdoor, Saad Jabbar Nghaimesh, and Mohannad Naeem Houshi. 2022. "Numerical Study on Pool Boiling of Hybrid Nanofluids Using RPI Model" Fluids 7, no. 6: 187. https://doi.org/10.3390/fluids7060187
APA StyleKamel, M. S., Albdoor, A. K., Nghaimesh, S. J., & Houshi, M. N. (2022). Numerical Study on Pool Boiling of Hybrid Nanofluids Using RPI Model. Fluids, 7(6), 187. https://doi.org/10.3390/fluids7060187