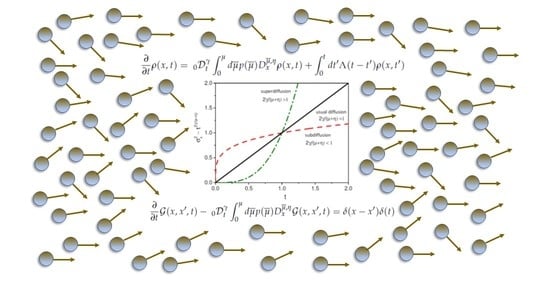
A Generalized Diffusion Equation: Solutions and Anomalous Diffusion
Abstract
:1. Introduction
2. Fractional Dynamics and Diffusion
3. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Meerschaert, M.M.; Sikorskii, A. Stochastic Models for Fractional Calculus; de Gruyter: Berlin, Germany, 2019. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Magin, R. Fractional calculus in bioengineering, part 1. Crit. Rev. Biomed. Eng. 2004, 32, 1–104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: Singapore, 2011. [Google Scholar]
- Evangelista, L.R.; Lenzi, E.K. Fractional Diffusion Equations and Anomalous Diffusion; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Kuntz, M.; Lavallée, P. Experimental evidence and theoretical analysis of anomalous diffusion during water infiltration in porous building materials. J. Phys. D Appl. Phys. 2001, 34, 2547. [Google Scholar] [CrossRef]
- Rosseto, M.P.; Evangelista, L.R.; Lenzi, E.K.; Zola, R.S.; Ribeiro de Almeida, R.R. Frequency-Dependent Dielectric Permittivity in Poisson–Nernst–Planck Model. J. Phys. Chem. B 2022, 126, 6446–6453. [Google Scholar] [CrossRef]
- Scher, H.; Montroll, E.W. Anomalous transit-time dispersion in amorphous solids. Phys. Rev. B 1975, 12, 2455. [Google Scholar] [CrossRef]
- Jeon, J.H.; Leijnse, N.; Oddershede, L.B.; Metzler, R. Anomalous diffusion and power-law relaxation of the time averaged mean squared displacement in worm-like micellar solutions. New J. Phys. 2013, 15, 045011. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L.; Zola, R.; Scarfone, A. Fractional Schrödinger equation for heterogeneous media and Lévy-like distributions. Chaos Solitons Fractals 2022, 163, 112564. [Google Scholar] [CrossRef]
- Magin, R.L.; Lenzi, E.K. Slices of the Anomalous Phase Cube Depict Regions of Sub-and Super-Diffusion in the Fractional Diffusion Equation. Mathematics 2021, 9, 1481. [Google Scholar] [CrossRef]
- Kenkre, V.; Montroll, E.; Shlesinger, M. Generalized master equations for continuous-time random walks. J. Stat. Phys. 1973, 9, 45–50. [Google Scholar] [CrossRef]
- Swenson, R.J. Derivation of generalized master equations. J. Math. Phys. 1962, 3, 1017–1022. [Google Scholar] [CrossRef]
- Cortes, E.; West, B.J.; Lindenberg, K. On the generalized Langevin equation: Classical and quantum mechanicala. J. Chem. Phys. 1985, 82, 2708–2717. [Google Scholar] [CrossRef]
- Klafter, J.; Sokolov, I.M. First Steps in Random Walks: From Tools to Applications; OUP Oxford: Oxford, UK, 2011. [Google Scholar]
- Giona, M.; Roman, H.E. Fractional diffusion equation on fractals: One-dimensional case and asymptotic behaviour. J. Phys. A Math. Gen. 1992, 25, 2093. [Google Scholar] [CrossRef]
- Hashan, M.; Jahan, L.N.; Imtiaz, S.; Hossain, M.E. Modelling of fluid flow through porous media using memory approach: A review. Math. Comput. Simul. 2020, 177, 643–673. [Google Scholar] [CrossRef]
- Razminia, K.; Razminia, A.; Baleanu, D. Fractal-fractional modelling of partially penetrating wells. Chaos Solitons Fractals 2019, 119, 135–142. [Google Scholar] [CrossRef]
- Raghavan, R.; Chen, C. The Theis solution for subdiffusive flow in rocks. Oil Gas Sci. Technol. Rev. D’Ifp Energies Nouv. 2019, 74, 6. [Google Scholar] [CrossRef]
- Zhokh, A.; Strizhak, P. Macroscale modeling the methanol anomalous transport in the porous pellet using the time-fractional diffusion and fractional Brownian motion: A model comparison. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104922. [Google Scholar] [CrossRef]
- Feng, C.; Si, X.; Li, B.; Cao, L.; Zhu, J. An inverse problem to simulate the transport of chloride in concrete by time–space fractional diffusion model. Inverse Probl. Sci. Eng. 2021, 29, 2429–2445. [Google Scholar] [CrossRef]
- Han, M.; Zhou, C.; Silberschmidt, V.V.; Bi, Q. Multiscale heat conduction and fractal oxidation behaviors of needle-punched carbon/carbon composites. Sci. Eng. Compos. Mater. 2022, 29, 508–515. [Google Scholar] [CrossRef]
- Lenzi, E.K.; Evangelista, L. Space–time fractional diffusion equations in d-dimensions. J. Math. Phys. 2021, 62, 083304. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with non-local and non-singular kernel. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Tateishi, A.A.; Ribeiro, H.V.; Lenzi, E.K. The role of fractional time-derivative operators on anomalous diffusion. Front. Phys. 2017, 5, 52. [Google Scholar] [CrossRef] [Green Version]
- Fernandez, A.; Baleanu, D. Classes of operators in fractional calculus: A case study. Math. Methods Appl. Sci. 2021, 44, 9143–9162. [Google Scholar] [CrossRef]
- Singh, H. Chebyshev spectral method for solving a class of local and nonlocal elliptic boundary value problems. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Singh, H. Solving a class of local and nonlocal elliptic boundary value problems arising in heat transfer. Heat Transf. 2022, 51, 1524–1542. [Google Scholar] [CrossRef]
- Singh, H. An efficient computational method for non-linear fractional Lienard equation arising in oscillating circuits. In Methods of Mathematical Modelling; CRC Press: Boca Raton, FL, USA, 2019; pp. 39–50. [Google Scholar]
- Singh, H.; Srivastava, H. Numerical investigation of the fractional-order Liénard and Duffing equations arising in oscillating circuit theory. Front. Phys. 2020, 8, 120. [Google Scholar] [CrossRef]
- Scarfone, A.M.; Barbero, G.; Evangelista, L.R.; Lenzi, E.K. Anomalous Diffusion and Surface Effects on the Electric Response of Electrolytic Cells. Physchem 2022, 2, 163–178. [Google Scholar] [CrossRef]
- Barbero, G.; Evangelista, L.; Lenzi, E.K. Time-fractional approach to the electrochemical impedance: The Displacement current. J. Electroanal. Chem. 2022, 920, 116588. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.; Nieto, J.J. Handbook of Fractional Calculus for Engineering and Science; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Singh, H.; Kumar, D.; Baleanu, D. Methods of Mathematical Modelling: Fractional Differential Equations; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Singh, H.; Kumar, D.; Baleanu, D. Methods of Mathematical Modelling: Infectious Disease; Elsevier Science: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Gómez-Aguilar, J.; Atangana, A. Fractional Hunter-Saxton equation involving partial operators with bi-order in Riemann–Liouville and Liouville–Caputo sense. Eur. Phys. J. Plus 2017, 132, 100. [Google Scholar] [CrossRef]
- Evangelista, L.R.; Lenzi, E.K. An Introduction to Anomalous Diffusion and Relaxation; Springer Nature: Berlin, Germany, 2023. [Google Scholar]
- Ali, I.; Kalla, S. A generalized Hankel transform and its use for solving certain partial differential equations. Anziam J. 1999, 41, 105–117. [Google Scholar] [CrossRef] [Green Version]
- Garg, M.; Rao, A.; Kalla, S.L. On a generalized finite Hankel transform. Appl. Math. Comput. 2007, 190, 705–711. [Google Scholar] [CrossRef]
- Nakhi, Y.B.; Kalla, S.L. Some boundary value problems of temperature fields in oil strata. Appl. Math. Comput. 2003, 146, 105–119. [Google Scholar] [CrossRef]
- Xie, K.; Wang, Y.; Wang, K.; Cai, X. Application of Hankel transforms to boundary value problems of water flow due to a circular source. Appl. Math. Comput. 2010, 216, 1469–1477. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Diffusion on fractals. Phys. Rev. A 1985, 32, 3073–3083. [Google Scholar] [CrossRef]
- O’Shaughnessy, B.; Procaccia, I. Analytical Solutions for Diffusion on Fractal Objects. Phys. Rev. Lett. 1985, 54, 455–458. [Google Scholar] [CrossRef]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. Math. Phys. Eng. Sci. 1926, 110, 709–737. [Google Scholar]
- Boffetta, G.; Sokolov, I.M. Relative Dispersion in Fully Developed Turbulence: The Richardson’s Law and Intermittency Corrections. Phys. Rev. Lett. 2002, 88, 094501. [Google Scholar] [CrossRef] [Green Version]
- Ben Avraham, D.; Havlin, S. Diffusion and Reactions in Fractals and Disordered Systems; CUP: Cambridge, UK, 2000. [Google Scholar]
- Su, N.; Sander, G.; Liu, F.; Anh, V.; Barry, D. Similarity solutions for solute transport in fractal porous media using a time- and scale-dependent dispersivity. App. Math. Model. 2005, 29, 852–870. [Google Scholar] [CrossRef] [Green Version]
- He, J.H. Fractal calculus and its geometrical explanation. Results Phys. 2018, 10, 272–276. [Google Scholar] [CrossRef]
- Cai, W.; Chen, W.; Xu, W. The fractal derivative wave equation: Application to clinical amplitude/velocity reconstruction imaging. J. Acoust. Soc. Am. 2018, 143, 1559–1566. [Google Scholar] [CrossRef]
- Chen, W.; Liang, Y. New methodologies in fractional and fractal derivatives modeling. Chaos Solitons Fractals 2017, 102, 72–77. [Google Scholar] [CrossRef]
- Liang, Y.; Chen, W.; Cai, W. Hausdorff Calculus: Applications to Fractal Systems; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2019; Volume 6. [Google Scholar]
- Evans, M.R.; Majumdar, S.N. Diffusion with stochastic resetting. Phys. Rev. Lett. 2011, 106, 160601. [Google Scholar] [CrossRef] [PubMed]
- Lenzi, M.K.; Lenzi, E.K.; Guilherme, L.; Evangelista, L.R.; Ribeiro, H.V. Transient anomalous diffusion in heterogeneous media with stochastic resetting. Phys. A Stat. Mech. Appl. 2022, 588, 126560. [Google Scholar] [CrossRef]
- Wyld, H.W.; Powell, G. Mathematical Methods for Physics; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Mathai, A.M.; Saxena, R.K.; Haubold, H.J. The H-Function: Theory and Applications; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Lenzi, E.K.; Evangelista, L.; Lenzi, M.K.; Ribeiro, H.V.; de Oliveira, E.C. Solutions for a non-Markovian diffusion equation. Phys. Lett. A 2010, 374, 4193–4198. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, M. The time fractional heat conduction equation in the general orthogonal curvilinear coordinate and the cylindrical coordinate systems. Phys. A Stat. Mech. Appl. 2010, 389, 3368–3374. [Google Scholar] [CrossRef]
- Evans, M.R.; Majumdar, S.N.; Schehr, G. Stochastic resetting and applications. J. Phys. A 2020, 53, 193001. [Google Scholar] [CrossRef]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lenzi, E.K.; Somer, A.; Zola, R.S.; da Silva, L.R.; Lenzi, M.K. A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids 2023, 8, 34. https://doi.org/10.3390/fluids8020034
Lenzi EK, Somer A, Zola RS, da Silva LR, Lenzi MK. A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids. 2023; 8(2):34. https://doi.org/10.3390/fluids8020034
Chicago/Turabian StyleLenzi, Ervin K., Aloisi Somer, Rafael S. Zola, Luciano R. da Silva, and Marcelo K. Lenzi. 2023. "A Generalized Diffusion Equation: Solutions and Anomalous Diffusion" Fluids 8, no. 2: 34. https://doi.org/10.3390/fluids8020034
APA StyleLenzi, E. K., Somer, A., Zola, R. S., da Silva, L. R., & Lenzi, M. K. (2023). A Generalized Diffusion Equation: Solutions and Anomalous Diffusion. Fluids, 8(2), 34. https://doi.org/10.3390/fluids8020034