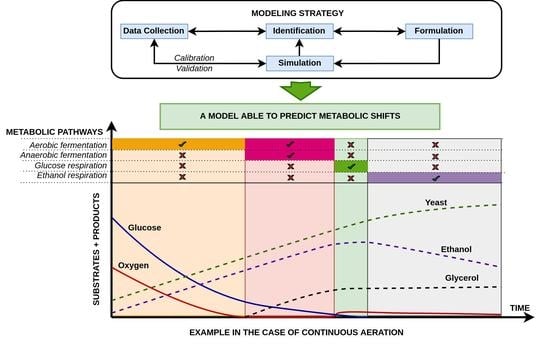
1. Introduction
Following the growing popularity of digital twins in bio-production [
1,
2,
3], mechanistic modeling has received renewed attention by the scientific community. Whatever the complexity of digital twins at the plant level, mechanistic models remain important, as they provide an excellent summary of available process knowledge. Although scientists and industry experts use these models efficiently, they can be further improved by machine learning, either using data taken from online sources or existing databases. In addition, such models are useful for planning experiments and determining which critical process variables need to be monitored and controlled tightly [
4]. More precisely, these mechanistic models allow a better understanding, description, and quantification of the phenomena involved in highly important and complex bioprocesses, such as alcoholic fermentation using the yeast
Saccharomyces cerevisiae.
Saccharomyces cerevisiae is a Crabtree-positive yeast of great importance for various biotechnological applications, some of which date back several thousands of years [
5]. This yeast strain is commonly used for its capacity to rapidly convert sugars to ethanol and carbon dioxide under both aerobic and anaerobic conditions [
6]. Although the Crabtree effect has been extensively studied, much remains to be well understood about this phenomenon. Under aerobic conditions, the alcoholic fermentation process occurs when the glucose concentration exceeds 0.10–0.15 g/L [
7], switching to the respiration process when the glucose concentration is below these values. Once the glucose is depleted, ethanol respiration takes place. Even under aerobic conditions, the anaerobic metabolic pathway can also be activated when the rate of biological oxygen uptake exceeds the rate of oxygen supply, which is identifiable by the production of glycerol. In the absence of molecular oxygen,
S. cerevisiae carries out the anaerobic fermentation process, producing glycerol for the cytosolic redox balance [
8].
The above observations confirm the complexity of yeast metabolism, and its use requires precise control of the process to obtain maximum productivity and quality products. Modeling has proven to be a powerful ally in explaining yeast metabolism and a useful tool for optimizing and controlling fermentation processes under aerobic and anaerobic conditions.
Several mechanistic yeast models have been developed using the typical Monod-type expression (
). This mathematical expression considers the limiting substrates as glucose, nitrogen and oxygen. Glucose is particularly important to
Saccharomyces cerevisiae, as it is by far the yeast’s preferred carbon source. Yeast cells can sense glucose and utilize it efficiently over a broad range of concentrations, from a few micromolars to even a few molars [
9]. Nitrogen is also an essential element in
S. cerevisiae’s composition, since it is mandatory for protein synthesis and represents 9% (
w/
w) of yeast biomass [
10]. Oxygen is required to regenerate the NAD
+ used in the glycolytic pathway of biomass formation, closing the redox balance for the co-enzyme system NAD
+/NADH. The oxidation of cytosolic NADH into NAD
can occur through mitochondrial respiration with external NADH dehydrogenase [
8,
11]. Oxygen is also important for the synthesis of yeast membrane compounds (sterols and unsaturated fatty acids) [
12], though this process could be neglected since the required amount is very weak, between 0.3 and 1.5 mgO
gDW
[
13].
Saccharomyces cerevisiae is a superb ethanol producer yet is also sensitive to higher ethanol concentrations, especially under high-gravity or very-high-gravity fermentation conditions. The term “gravity” (actually specific gravity) is commonly used in the fermentation industry to indicate the dissolved solids content of the fermentation medium. The progress of fermentation is usually monitored by measuring the specific gravity of the medium. Very-high-gravity (VHG) technology for fuel alcohol production is defined as “the preparation and fermentation to completion of mashes containing 27 or more grams of dissolved solids per 100 g mash” [
14]. The application of VHG fermentation technology, i.e., the use of highly concentrated sugar substrates, for the industrial production of bioethanol has a number of benefits, including decreased process water requirements, energy costs and bacterial contamination risk, increased overall plant productivity and higher ethanol concentrations in the fermentation product that allow considerable savings in energy for distillation [
15,
16,
17]. High contents of saccharides in fermentation medium cause an increase in the osmotic pressure, which has a detrimental effect on yeast cells. However,
Saccharomyces cerevisiae, which is commonly used for ethanol production, can ferment an increased amount of sugars in the medium, when all the other required nutrients are in adequate amounts [
18]. High ethanol concentrations are the major stress factor during VHG fermentation, but fortunately, many strains of
S. cerevisiae are tolerant to very high ethanol concentrations even without genetic manipulation [
19]. Research in yeast physiology has revealed that many strains of
S. cerevisiae can potentially tolerate far higher ethanol concentration than previously believed [
19,
20], usually without any conditioning or genetic modifications.
Ethanol tolerance is associated with the interplay of complex networks at the genome level. Although significant efforts have been made to study the ethanol stress response in past decades, mechanisms of ethanol tolerance are not well known [
21,
22]. Eukaryotic cells have developed diverse strategies to combat the harmful effects of a variety of stress conditions. In the model yeast
Saccharomyces cerevisiae, the increased concentration of ethanol as the primary fermentation product will influence the membrane fluidity and be toxic to membrane proteins, leading to cell growth inhibition and ultimately death [
23].
These limiting substrates’ and by-products’ inhibition effect on yeast growth rate should be considered in any model describing the metabolism of this complex yeast in order to adequately describe the fermentation process under both aerobic and anaerobic conditions. Each limiting substrate can be easily included in the model with the Monod-like function, and several alternative expressions exist for the inhibiting by-products’ effects [
24,
25,
26,
27,
28,
29,
30]. However, the Monod-like function and even the conventional expression used by computer scientists to shift from a limiting substrate to an inhibiting one (
) are not suitable to model the shift between aerobic fermentation and respiration in the particular case of the Crabtree effect. This phenomenon requires a more precise switching function that allows aerobic fermentation to be turned off and glucose respiration to be turned on when glucose concentration falls under 0.10–0.15 g/L. Several models have already been developed to simulate the fermentation process with
Saccharomyces cerevisiae, achieving significant advances in its metabolism description [
26,
27,
31,
32,
33,
34,
35,
36]. However, much work remains to be done to increase the accuracy of the models in terms of triggering/inhibiting metabolism pathways when the environmental conditions change.
The main objective of this work is to propose an accurate mechanistic model capable of predicting the metabolic shift from glucose aerobic fermentation to glucose respiration when the glucose concentration is lower than 0.10–0.15 g/L and to ethanol respiration once glucose is depleted. This mechanistic model is developed to be as simple as possible, easy to use, and adaptable to the conditions of each system. The model can be adapted to a significant number of existing mutated yeast strains used currently in the industry. In addition, the model activates/deactivates simultaneous anaerobic fermentation in the absence/presence of dissolved oxygen, respectively. This integral model will be calibrated by combining experimental data generated using a commercial yeast strain Saccharomyces cerevisiae used for wine production and modeling in an inverse method where the metabolic pathways’ stoichiometry and kinetics are determined independently when possible.
4. Results and Discussion
4.1. Modeling Yeast Activity under Completely Anaerobic Conditions
Table 3 summarizes the stoichiometry and kinetics parameters of the biological model under completely anaerobic conditions (anaerobic sub-model), which were obtained from the calibration procedure. As explained above, stoichiometry was obtained experimentally under completely anaerobic conditions, while kinetics were determined by inverse analysis. The inverse analysis combined experimental data and modeling using three experimental data sets obtained for different glucose, ethanol and yeast concentrations (experiments A, B, and C).
The optimization process using the PSO method converged to a unique minimum, which is demonstrated by the low standard deviation values obtained for each parameter during the optimization process (below 0.5%, as can be seen in
Table 3). Using the optimal parameters, the model was able to reproduce all the experiments, reporting a global mean relative error for all variables of 7% and with a unique set of parameters (
Table 4).
Interestingly, the maximum growth rate obtained during the calibration process is the same reported by Verduyn et al. [
44] (0.31 h
), which validates the quality of the calibration process. On the other hand, the value of the half-saturation coefficient obtained for glucose (1.72 g/L) reveals a larger need for this source of carbon in relation to what is reported in the literature (1 × 10
to 0.5 g/L) [
26,
27,
31,
32,
33,
34,
35,
36]. Similarly, the high value obtained for the half-saturation coefficient for ethanol inhibition (202.83 g/L) indicates that
S. cerevisiae has a high tolerance to ethanol under anaerobic conditions, significantly higher than those reported in the literature (10–26.97 g/L) [
26,
27].
The model provides very good results in the prediction of the variables’ behavior (
Table 4,
Figure 5); however, the half-saturation coefficient for ethanol inhibition obtained in this model might not be adequate to simulate anaerobic fermentation processes when dealing with higher ethanol concentrations. According to the inhibition function used in the model and the value of the half-saturation coefficient found for ethanol inhibition, the growth rate would be divided by a factor of two for an ethanol concentration of 202.83 g/L. However, according to Arroyo-López et al. [
45], no yeast activity should be observed at this concentration.
The high value of the half-saturation coefficient for ethanol inhibition results from the combination of both the experimental range of ethanol tested here and the shape of the inhibition function, which is too loose to account for toxicity. This problem could be solved with a recalibration process using a wider ethanol concentration range and a different mathematical expression for the inhibition function. For example, applying the
function (Equation (
7)) would involve a critical value (the ethanol concentration value above which no yeast activity is observed) and the range of inhibitory effect (
). This approach could be useful for future modeling research.
In general, the values obtained for the half-saturation coefficients for glucose and ethanol inhibition through the inverse analysis are outside the ranges reported in the literature. Yet these values describe very well the behavior of the main variables of the model. This is an interesting result since it is the first time, to our knowledge, that these parameters have been differentiated in yeast metabolic models for aerobic and anaerobic conditions. The model is consequently more accurate in describing the phenomena since it uses different substrate affinities and inhibitions for each operating condition.
The accuracy of the model for predicting the experimental data was quite good, reporting the highest MRE in predicting glucose concentration and satisfying the adequate description of the trends of all variables in the experimental data (
Table 4,
Figure 5).
In addition, the correlation analysis between the experimental data and the output variables of the model performed in this study is statistically significant, as its
p-values are less than 1 × 10
%, which is well below what is expected to achieve acceptable quality (
p ≤ 5%).
Figure 5 confirms that the model is able to reproduce the behavior of the main experimental variables very well, thus validating the description of the phenomena considered in the model. Even the lowest MRE value obtained for ethanol, the worst variable trend of the model reporting the lowest R-squared value, is still good (
Figure 5).
In general, the agreement between the three sets of experimental data and the model outputs is very strong, reporting an overall MRE value in the prediction of all the variables studied of less than 7%. In addition, the model is able to predict yeast metabolism under fully anaerobic conditions at different concentrations of glucose, ethanol, and yeast. These results confirm the robustness of the model and the quality of the calibration method.
4.2. Modeling Yeast Activity under Aerobic Conditions
Modeling the fermentation process under aerobic conditions is more complex, since it involves different metabolic pathways, such as aerobic fermentation and respiration processes, typical of a Crabtree effect positive yeast. The anaerobic fermentation pathway could be also included: even under aerobic conditions, the oxygen uptake can be larger than the rate of dissolved oxygen, partially triggering the anaerobic pathway. This metabolic pathway is verified by the data concerning glycerol production. The dissolved oxygen deficiency also worsens with time due to the decreased oxygen solubility in the medium, which is caused by an increased temperature resulting from metabolic heat release and the increase in the yeast population. Fortunately, the model accounts for these two effects of the anaerobic pathway and the influence of temperature on dissolved oxygen. Different glucose affinity and ethanol inhibition coefficients under aerobic and anaerobic conditions were established in the model, assuming that yeast tolerance to ethanol and affinity for glucose is different under aerobic and anaerobic conditions.
Three test combinations with different initial concentrations of glucose, ethanol, and yeast were performed to consider their influence on yeast kinetics (experiments D, E, and F). Most of the model parameters were taken from the literature, so only four parameters had to be calibrated, considerably simplifying the model calibration process. This simplified calibration process demonstrates the phenomenological character of the model, its universality, and its versatility for use in production.
The optimization process used the PSO method converged to a single minimum (
Table 5), reporting a standard deviation in parameter optimization of less than 0.25%.
The model was able to reproduce all experiments, reporting a global mean relative error for all variables of less than 11% (
Table 6). In this case, a half-saturation coefficient for ethanol inhibition (19.70 g/L) was obtained under aerobic conditions, which was lower than the same value of the half-saturation coefficient for ethanol inhibition under anaerobic conditions. The differences between these values supports this work’s assumption, i.e., that yeast tolerance to ethanol is different under anaerobic and aerobic conditions (10-fold more tolerant under anaerobic conditions). Arroyo-López et al. [
45] studied the inhibitory effect of ethanol using the Lambert and Pearson [
46]’s methodology for the estimation of the minimum inhibitory concentration (MIC) and non-inhibitory concentration (NIC) of a compound using optical density (OD) measurements. The MIC is related to the resistance or tolerance of the microorganism to the compound and is the lowest concentration that results in the maintenance or reduction of an inoculum’s viability (marks the concentration above which no growth is observed). In contrast, the NIC is related to the susceptibility of the microorganism to the compound, and it is the concentration above which the inhibitor begins to have a progressive and negative effect on growth [
46]. The authors studied some yeast strains, and in the particular case of
S. cerevisiae, they obtained values for the NIC and MIC in the ranges of (36.7–73.9 g/L) and (95.6–141.4 g/L), respectively. In our experiments, the ethanol inhibition effect was only observed in the data set in which an initial ethanol concentration over 50 g/L concentration was used, which lies well within the inhibitory concentration ranges reported by Arroyo-López et al. [
45].
According to the stoichiometry and kinetics obtained in the present study, the aerobic fermentation process has a lower ethanol production yield, a higher yeast yield, and a higher growth rate than the anaerobic fermentation process. According to Thierie [
33], stoichiometry varies as a function of the specific growth rate of the yeast. In contrast, our work uses constant stoichiometric parameters corresponding to the mean values of the experiments performed for the individual metabolic pathways under aerobic and anaerobic conditions (
Table 3 and
Table 5). However, in all batch fermentation processes carried out in this study, the apparent stoichiometry varies due to the varying partition of the metabolic pathways. Accounting for the varying metabolic pathways partition confers a much better predictive capability on the model. Our model thus has the potential to increase ethanol yield with reduced consumption of time and resources, which would be useful for all ethanol producers.
Figure 6 summarizes the results obtained with the final set of parameters.
In most cases, the model is able to predict the concentrations over time with accuracy. The highest MRE values and the lowest R-squared values were found for glycerol (an MRE of 24.19% and an R-squared of 93.30% for the worse cases, experiment D and E, respectively) (
Table 6,
Figure 6). Once again, the correlation analysis between the experimental data and the output variables of the model performed in this study is statistically significant, as its p-values are less than 1 × 10
%.
S. cerevisiae has already been shown to grow by using glycerol as a carbon source under aerobic conditions at low specific growth rates (0.01–0.20 h
) [
47]. Interestingly, glycerol consumption was observed in experiments E and F beyond 6 h. Yeast growth based on glycerol under aerobic conditions was not included in the model, which might significantly affect the model balance. Improving this yeast model by including this metabolic pathway would be a novel approach and would require the identification of its main metabolites, their stoichiometry, and kinetics.
4.3. Model Validation: Yeast Culture without Gas Injection
Our model was validated using a batch fermentation process without gas injection (experiment G) instead of the experiments from the learning database. In this experiment, the gas headspace of the bioreactor was maintained at a constant atmospheric pressure. Even without air injection, oxygen is still transferred from the bioreactor gas headspace to the liquid volume through the agitation process. This oxygen transfer occurs through the oxygen concentration gradient maintained by the biological oxygen consumption in the liquid phase. Consequently, both anaerobic and aerobic metabolic pathways take place simultaneously. In the simulation, the
value was replaced by the oxygen transfer mass from the gas headspace, taking the value already estimated by La et al. [
35] for the same installation and operation conditions (
s
).
As can be seen in
Table 7 and
Figure 8, the model performs very nicely for this validation test. It allows all variables’ evolution to be predicted with an MRE of less than 11%, reporting a global MRE for all variables of 7%. The trends of all variables were well described, showing a very good correlation coefficient value above 99% (
Figure 8), results that are statistically significant as their
p-values are less than 1 × 10
%. The model also provides an excellent prediction of glycerol production. These results validate the quality, applicability, and accuracy of the model, even under different operating conditions.
Figure 9 depicts the individual metabolic pathway contributions during glucose consumption and ethanol production without gas injection.
Even without gas injection, the aerobic metabolic pathway was partly activated thanks to the oxygen transfer from the gas headspace. This limited mass transfer explains the low activation of the aerobic metabolic pathway compared to the dominant metabolism of the anaerobic pathway. Most of the glucose consumption and ethanol production were associated with the anaerobic metabolic pathway (94.5% and 95.9%, respectively). No ethanol consumption was observed during the experiment, as
Figure 9 confirms.
Indeed, this particular case of yeast culture without gas injection more closely resembles real-world scenarios, where alcoholic fermentation processes are partially carried out under anaerobic conditions. Certain designs of bioreactors can allow the oxygen in the gas headspace to be continuously renewed if atmospheric air is allowed to enter, for example, through filters. The line graphs in
Figure 9 prove that the model is able to activate/deactivate the corresponding metabolic pathways according to the medium conditions and, more importantly, under different operating conditions than those used for model calibration. The results obtained allow a better understanding of the phenomena occurring in partial anaerobic systems in order to improve process control and optimize operating conditions according to the conditions of the medium.
4.4. Potential Application of This Model
Producers and scientists currently consider modeling to be a promising tool for enhancing bio-production. To this end, databases, mechanistic models, and machine learning need to work in synergy for online process monitoring. This approach is known as hybrid modeling and offers a promising route in the general quest of the digital twin in bio-production [
1,
2,
3]. For this approach to be efficient, the mechanistic model needs to be as predictive as possible. The mechanistic model could be improved either inline by the real-time tuning of some key parameters or online using a dynamic learning database.
Even though the mechanistic model was applied to a specific commercial strain of Saccharomyces cerevisiae, the general modeling approach proposed in this study is a perfect brick for hybrid modeling for any application of bio-production. Our model is constructed for this commercial strain by including the main metabolic pathways of mutant and wild-type yeast strains used for ethanol or yeast production reported in the literature. The model was successfully calibrated and validated for the commercial yeast strain provided by the Institut Oenologique de Champagne under the name IOC Fizz+, thus demonstrating its applicability and universality in ethanol or yeast production systems. It is important to note that, for predicting the metabolism of other yeast strains, model calibration alone may be sufficient if the mutated yeast strain exhibits the same metabolic pathways described in the model. The structural basis of the model can allow other metabolic pathways to be easily included or removed when describing the metabolism of the microorganisms that do not exhibit the same metabolic pathways more accurately.
The predictive model proposed in this paper is valuable not only for alcoholic fermentation but also for other processes, such as the production of chemicals, fuels, foods, and pharmaceuticals, as yeast is one of the most widely used hosts for synthetic biology [
48]. One of the disadvantages of the Crabtree effect is the carbon loss due to the ethanol production under aerobic conditions, which leads to a lower biomass formation and consequently a lower production of recombinant proteins [
49]. Therefore, the structural base of the developed model could be adapted or serve as a basis for the modeling of other Crabtree-positive yeasts used for the production of therapeutic proteins. The model could then be used as a tool for achieving a better understanding, control, and optimization of the production process.
Beyond the huge domain of engineered yeast strains, the formulation proposed in this work can also be applied to other strains. In particular, the proposed functions that account for the activation or inhibition of pathways and sudden shifts of pathways are universal. For example, our team is currently using this framework to model the Chinese hamster ovary (CHO) cell metabolism to produce antibodies. CHO cells are analogous with the Crabtree effect in that they exhibit a phenomenon known as the Warburg effect, where glucose is fermented to produce lactate even in the presence of oxygen [
50]. Even in the presence of oxygen, this first stage of lactic fermentation corresponds to a peak of exponential cell growth, followed by a metabolic shift from the net production to the net consumption of lactate (known as the stationary phase) during which proteins are produced. The similarity between the systems mentioned above suggests that our mechanistic models have the potential to predict the metabolic shift observed for CHO cells, which has the possibility of considerably improving the current state of CHO cell modeling.
Finally, bringing together mechanistic modeling and machine learning can better explain system phenomena that are traditionally difficult to describe. For instance, well-established theoretical knowledge can be formulated as explicit equations, while parameters that cannot be derived from first principles or space-time-varying (latent) states are estimated via a machine learning approach [
51]. The development of online sensors using the Raman spectroscopy mechanistic and machine learning models and their hybridization variants have considerably increased their application in bioprocess retro-control, allowing maximum productivity with lower resource consumption.
5. Conclusions
In this study, a robust and predictive yeast model was developed and successfully validated with experimental data from experiments with a commercial yeast strain used for wine production. The model includes a comprehensive set of metabolic pathways that are always present in the model but are more or less activated depending on the growth conditions. A general framework is proposed for the formulation, including functions that account for the activation, inhibition, and shift of metabolic pathways.
Known parameters were taken from the literature, and the remaining parameters were estimated by inverse analysis using the particle swarm optimization method. In all cases, the optimization process using the PSO method converged to a single minimum, reporting a standard deviation in parameter optimization of less than 0.5%. The evaluation of the optimized set of stoichiometric and kinetic parameters on the model allows for the accurate prediction of concentrations over time, reporting global mean relative errors for all variables of less than 7 and 11% under completely anaerobic and aerobic conditions, respectively.
The obtained model is able to switch between aerobic fermentation and glucose-based respiration when the glucose reaches values below 0.10–0.15 g/L. It is also able to activate the anaerobic fermentation metabolic pathway even under aerobic conditions when the rate of oxygen uptake is higher than the rate of dissolved oxygen, as supplied by aeration. Once glucose is depleted under aerobic conditions, the model automatically switches to ethanol degradation.
The model quality and robustness were confirmed with an additional experiment performed without gas injection, and the model describes the main process variables with an overall mean relative error of 7%. The complete formulation and set of parameters are provided in the document so that the reader can implement them for their own needs.
The results provided in this work give new insights towards the behavior of S. cerevisiae. For example, the model better informs the emerging nature of the global stoichiometry and differences in ethanol tolerances, which depend on the evolution of yeast growth conditions over time and the active metabolic pathway. Beyond the application to the yeast strain studied here, this work gives a general framework of mechanistic modeling able to predict the coexistence of several metabolic pathways and their shift along the growth conditions. This framework can be used as a building block of a digital twin of any bio-production.