Next Article in Journal
Influence of Na/Mg Co-Doping in Tuning Microstructure, Transport, Optical, and Magnetic Properties of TiO2 Compounds for Spintronics Applications
Next Article in Special Issue
Mononuclear Heptacoordinated 3d-Metal Helicates as a New Family of Single Ion Magnets
Previous Article in Journal
Magnetic Properties and Microstructure of Ce-Cu-Al Low Melting Alloy Bonding Sm2Fe17N3 Magnet Fabricated by the Hot-Pressing Method
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Magnetochemistry
Volume 8
Issue 11
10.3390/magnetochemistry8110151
magnetochemistry-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect of Ligand Substitution on Zero-Field Slow Magnetic Relaxation in Mononuclear Dy(III) β-Diketonate Complexes with Phenanthroline-Based Ligands

by
Egor V. Gorshkov
1,2,
Denis V. Korchagin
1,*,
Elena A. Yureva
1,*,
Gennadii V. Shilov
1,
Mikhail V. Zhidkov
1,
Alexei I. Dmitriev
1,
Nikolay N. Efimov
3,
Andrew V. Palii
1 and
Sergey M. Aldoshin
1
1
FRC Problems of Chemical Physics and Medicinal Chemistry, Russian Academy of Sciences, 142432 Chernogolovka, Russia
2
Faculty of Fundamental Physical and Chemical Engineering, Moscow State University, 119991 Moscow, Russia
3
N. S. Kurnakov Institute of General and Inorganic Chemistry, Russian Academy of Sciences, 119991 Moscow, Russia
*
Authors to whom correspondence should be addressed.
Magnetochemistry 2022, 8(11), 151; https://doi.org/10.3390/magnetochemistry8110151
Submission received: 14 October 2022 / Revised: 31 October 2022 / Accepted: 4 November 2022 / Published: 7 November 2022
(This article belongs to the Special Issue New Advances in Single-Molecule Magnets)
Browse Figures
Versions Notes

Abstract

:
Herein, we report the synthesis, structure and magnetic properties of two mononuclear complexes of general formula [Dy(acac)3(L)], where L = 2,2-dimethyl-1,3-dioxolo[4,5-f][1,10] phenanthroline (1) or 1,10-phenanthroline-5,6-dione (2), and acac− = acetylacetonate anion. A distorted square-antiprismatic N2O6 environment around the central Dy(III) ion is formed by three acetylacetonate anions and a phenanthroline-type ligand. Both complexes display a single-molecule magnet (SMM) behavior at zero applied magnetic field. Modification of the peripheral part of ligands L provide substantial effects both on the magnetic relaxation barrier Ueff and on the quantum tunneling of magnetization (QTM). Ab initio quantum-chemical calculations are used to analyze the electronic structure and magnetic properties.

Graphical Abstract

1. Introduction

Lanthanide ions are the most promising ones for designing mononuclear single molecule magnets (SMMs), since 4f ions show rather strong magnetic anisotropy associated with the unquenched orbital angular momentum in combination with relatively weak spin-phonon interaction [1,2,3,4,5]. Mononuclear LnIII SMMs are mainly based on highly magnetically anisotropic DyIII, TbIII, HoIII, and ErIII ions [6,7,8,9].
The dominant factors influencing the magnetic relaxation properties of LnIII SMMs are the electronic configuration of the ion, the coordination geometry determining the crystal field splitting and hence the single ion anisotropy, as well as dipole-dipole interactions between lanthanide ions [5,10]. Unfortunately, it is hard to elucidate the influence of only one of these factors by fixing the rest of them. Thus, a change in the coordination geometry (or, alternatively, in crystal field) inevitably entails a change in the crystal packing and, as a consequence, intermolecular interactions. To reduce the number of variable parameters, it is convenient to compare families of related compounds. For example, plenty of bis(phthalocyaninato) lanthanide double-decker complexes with different substituents at the phthalocyanine center and D4d geometry of coordination environment have been reported. It has been observed that the effect of the substituents through the change in the crystal field has a strong influence on the SMM behavior of these complexes [5,7].
Lanthanide complexes with D4d symmetry have recently been the subject of comprehensive study [11,12]. Another widely studied family includes complexes of general formula [DyIII(β-diketonate)3(L)]. Note, that there are much more hexafluoroacetylacetonate-based (hfac−) complexes than acetylacetonate (acac−) ones. A rough analysis of the Cambridge Structural Database (CSD) [13] on mononuclear eight-coordinate complexes [Dy(β-diketonate)3(L)] has yielded about 225 compounds for β-diketonate = hfac− and only 21 complexes for acac−. Among them, a slow magnetic relaxation behavior has been reported for 20 and seven complexes, respectively. In addition to acac and hfac, a variety of β-diketonates with different substituents at 3,5-positions are known. Despite the great diversity of the studied complexes, it has been recently shown [14,15] that acetylacetonate-based complexes are more promising for SMMs design. Indeed, the studies of two mononuclear complexes [Dy(acac)3(tmphen)] and [Dy(hfac)3(tmphen)] (tmphen = 3,4,7,8-tetramethyl-1,10-phenanthroline) have revealed that the energy barrier (Ueff) of the acac-based complex (130 K) is much higher than that of the hfac one (35 K) [14]. Later on, in [15] the advantage of acac over tta-anion (tta = 4,4,4-trifluoro-1-(2-thienyl)-1,3-butanedionate) has been also demonstrated (the found barriers are Ueff = 112 cm−1 (162 K) and 22 cm−1 (32 K), respectively).
Another way to control the crystal field in [Dy(β-diketonate)3(L)] complexes is to vary the auxiliary phenanthroline (phen) or bipyridine (bipy) ligand L. The size effect of a neutral phenanthroline-type ligand has been analyzed for [Dy(acac)3(L)] family, where L—phen, dpq, dppz, and dppn[16,17,18]. The transition from phen to larger polyaromatic systems (dpq and dppz) results in increasing the energy barriers (64, 136 and 187 K for phen, dpq and dppz, respectively) [16,17], however by using a larger dppn ligand one cannot further increase the barrier [18]. This observation has been explained in terms of an electrostatic interaction model [19,20]. A similar result has been obtained for the family of [Dy(thd)3(L)] complexes (thd = 2,2,6,6-tetramethyl-3,5-heptanedione) with the same N-capping ligands phen, dpq, and dppz [21]. A comparison of bipyridine and phenanthroline in [Dy(tta)3(L)] has also revealed the effect of the ligand substitution on the barrier height [22]. In addition, a large number of complexes have been studied that do not follow any trend [10,23,24,25].
Herein we report two new acetylacetonate complexes [Dy(acac)3(dmdophen)] (1) and [Dy(acac)3(phendione)]·CH3CN (2). As auxiliary neutral ligands we use 2,2-dimethyl-1,3-dioxolo[4,5-f][1,10]phenanthroline (dmdophen, 3) and 1,10-phenanthroline-5,6-dione (phendione, 4) (Figure 1). Dmdophen and phendione differ in the peripheral substituents, which, however, can have a dual effect on SMM characteristics. The first factor is donor or acceptor substituents, which are able to fine-tune the crystal field. The diketone-group of phendione is a strong electron density acceptor, while the dimethyldioxolo group of dmdophen is an electron donor. The second factor is the influence on intermolecular interactions. Two ketone oxygen atoms of phendione are open and can potentially form hydrogen bonds; in dmdophen, these oxygen atoms are sterically hindered by a bulky substituent. Along with the investigation of the crystal structure and magnetism of 1 and 2, we report their ab initio quantum chemical modeling.

2. Results and Discussion

Complexes [Dy(acac)3(dmdophen)] (1) and [Dy(acac)3(phendione)]·CH3CN (2) were obtained by the reaction of Dy(acac)3·3H2O (5) with equimolar amount of dmdophen (3) or phendione (4).

2.1. Crystal Structure of 1 and 2

Both complexes 1 and 2 crystallize in triclinic system, space group P-1 (Table S1 in the Supplementary Materials) with one mononuclear complex in asymmetric units. The Dy(III) ions are eight-fold coordinated by six oxygen atoms from three acac− ligands and two nitrogen atoms from one neutral phenanthroline-type ligand (Figure 2). The average Dy–N bond lengths are 2.62 and 2.60 Å for complexes 1 and 2, respectively (Table S2). The average Dy–O bond lengths are 2.32 Å for both complexes, but there is a pattern in the lengths of Dy–O bonds (Table S2). Thus, in crystal structure of 1, each acac group has equivalent Dy–O bond lengths, but this length varies from group to group. In acac groups of complex 2, these bonds are non-equivalent as well.
To analyze the exact geometry of these eight-coordinate Dy(III) complexes we have used a SHAPE 2.1 software [26,27]. The calculated parameter (Table S3) indicates that coordination environment of the Dy(III) ions can be regarded as eight-coordinate square-antiprismatic (SAP) polyhedron (D4d) with continuous shape measures (CShMs) of 0.679 and 0.543 for 1 and 2, respectively.
Deviations from the ideal D4d symmetry can be estimated from the parameters shown in Figure 3 [28,29]. The average values are dpp = 2.627 and din = 2.812 Å for 1; dpp = 2.592 and din = 2.822 Å for 2. This indicates axially compressed SAP geometry with dpp < din for both complexes. The skew angles, Φ, are 45.5° (1) and 45.7° (2), which are close to those for the highest SAP symmetry. Larger values of α = 56.4° (1) and 56.8° (2) (α > 54.74°) correspond to slight compression along the tetragonal axis. The angles between the upper and lower faces of the square antiprism are 2.56° and 2.40° for 1 and 2, respectively.
In addition, there are both intermolecular and intramolecular short contacts coexisting in 1 and 2 (Figure S5). In both complexes, the intramolecular contacts are similar and are formed by hydrogen atoms in 2-position of the phenanthroline fragment with oxygen atoms of the acetylacetonate groups. Moreover, in the crystal packing of 2, both keto-oxygen atoms O7 and O8 form short intermolecular contacts with hydrogen atoms in 2-position of the phenanthroline fragment of the neighboring molecule, forming a supramolecular assembly. This is not observed in the crystal packing of 1, where oxygen atoms O7 and O8 are sterically hindered. The acetonitrile solvent molecule in the crystal packing of 2 forms the short contact with C40–C41 bond bearing diketone-group. The shortest intermolecular Dy···Dy distances are 9.584 and 8.667 Å for 1 and 2, respectively.

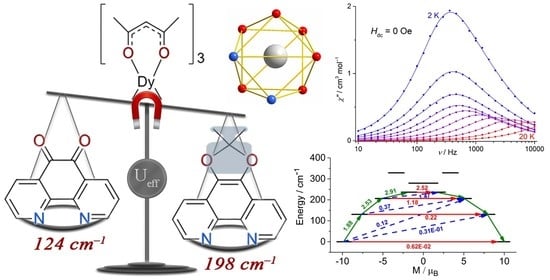
2.2. Magnetic Properties

The DC magnetic susceptibility data for both complexes 1 and 2 have been measured in the temperature range of 2.0–300 K at applied field 5000 Oe (Figure 4). The χMT values at room temperature are 13.66 and 13.86 cm3 K mol−1 for 1 and 2, respectively, which is in agreement with the expected value for the isolated Dy(III) ion (6H15/2, g = 4/3). The χMT values gradually decrease upon cooling from 300 to 10 K, and then undergo abrupt decrease, reaching values 8.53 and 8.26 cm3 K mol−1 at 2 K for 1 and 2, respectively (Figure 4). Magnetization (M) versus field curves for 1 and 2 at 2, 4, and 6 K are shown in insets to Figure 4. Both complexes exhibit quite similar M(H) dependences with the values of 5.02 Nβ and 5.04 Nβ at 5000 Oe for 1 and 2, respectively.
Both complexes 1 and 2 show SMM properties at zero applied field as evidenced by the presence of the frequency and temperature dependent maxima of the out-of-phase χM″ component of the AC magnetic susceptibility (Figure 5a,b). The relaxation times τ at 2 K are 0.5 and 3.4 ms for 1 and 2, respectively. The frequency dependences of the in-phase χM’ component of the magnetic susceptibility and the Cole-Cole diagrams are given in the Supplementary Materials (Figures S6 and S10). As the temperature increases, the intensity of the maxima decreases sharply without a shift in frequency thus indicating a temperature-independent relaxation regime. Temperature-dependent relaxation processes dominate above 10 K since positions of the maxima move with temperature. The relaxation times at 10 K are found to be 0.3 ms for 1 and 1.5 ms for 2. Positions of the maxima reach the upper limit for the AC frequency measurement range ν = 104 Hz at 18 K and 21 K for 1 and 2, respectively.
It should be noted that for complex 1 at low temperatures, an asymmetric broadening of the maximum on the frequency dependence of χM″ is observed, which cannot be described by the broadening parameter α in the generalized Debye model. Instead, the two-component Debye model has to be used to properly fit the experimental data in the temperature range of 2–12 K. In the meantime, the generalized Debye model fits the experimental data rather well at temperatures above 14 K (Table S4). The origin of the second component remains unclear and we will not focus on it in further discussion. Note only that such an effect was earlier observed for cobalt (II) system exhibiting SMM properties at zero DC field [30]. The presence of two relaxation processes in dysprosium complexes has been already reported [31,32].
The optimal DC field has been determined from the frequency dependences of χM′ and χM″ at 10 K and the applied fields in the range of 0–5000 Oe (Figures S7 and S11). The field dependences of the relaxation time τ (Figures S8 and S12) show that quantum tunneling of magnetization (QTM) dominates at low fields. Suppression of QTM resulting in elongation of relaxation times is observed at 1000–2000 Oe DC field.
At the optimal DC field (H = 1000 Oe) the relaxation time significantly increases (Figure 5c,d). Thus, at 10 K τ = 1.8 ms for 1 and 6.8 ms for 2. Although positions of the maxima reach the upper limit of the AC frequency measurement range ν = 104 Hz exactly at the same temperatures as in the case of zero DC field.
The Arrhenius plots of the ln(τ) are non-linear (Figure 6), indicating the contribution of processes other than Orbach. Fitting to the experimental data at zero and 1000 Oe DC field was performed according to the following equation, which includes two temperature-dependent relaxation processes, Orbach and Raman, as well as temperature-independent QTM process.
τ−1 = τ0−1·exp(−Ueff/kBT) + CTn+ τQTM−1
The best-fit parameters are shown in Table 1. It can be seen that at low temperatures and zero DC field, the QTM process dominates for both complexes, while the Raman and Orbach processes dominate at temperatures above 10 K. At the applied DC field, there is no contribution of QTM, while the Raman and Orbach processes remain. The involvement of the direct process τ−1 = AH4T is not required for a correct description of the ln(τ) vs. 1/T dependences for both complexes. Additionally, for both complexes, the temperature dependences of the relaxation time merge at temperatures close to 20 K (Figure 5). It can be assumed that τ becomes almost field-independent in the high-temperature region, which indicates the dominance of the Orbach process. The values of the energy barrier Ueff extracted from the fits prove to be the same at zero and 1000 Oe DC fields. It can be also seen that Ueff values are much higher for 1 than for 2.
Table
Table 1. Best-fit parameters for relaxation processes occurring in 1 and 2 at zero and 1000 Oe DC field.
Table 1. Best-fit parameters for relaxation processes occurring in 1 and 2 at zero and 1000 Oe DC field.
Parameter12
Hdc, Oe0100001000
Ueff, cm−1198(2)197(1)124(10)123(6)
τ0, s1.1(2)·10−111.5(1)·10−114.9(9)·10−94.5(7)·10−9
CRaman, s−1 K−n8.0(9)·10−31.21(8)·10−41.3(6)·10−24.3(8)·10−3
nRaman5.3(2)6.65(2)4.4(7)4.4(9)
τQTM, s4.8(4)·10−4-2.9(6)·10−3-
In addition, complexes 1 and 2 show different QTM contributions. It can be seen that relaxation time τQTM for 1 is about an order of magnitude shorter than for 2. This is somewhat unexpected, since there are both intra- and intermolecular short contacts in 2 that form a supramolecular assembly. Usually, the complexes experience a stronger QTM effect because of the existence of intermolecular interactions [33]. The most effective way to experimentally assess the effect of intermolecular interactions on QTM is the study of isostructural diamagnetic derivatives (usually Y) doped with a small amount of Dy analogues [34,35]. Relaxation time τQTM and the energy barrier Ueff height are not related to each other. For example, a compound with a high barrier can have a large contribution from QTM and vice versa [15].
All mononuclear complexes of general formula [DyIII(acac)3(L)] with bidentate ligand L known to date are shown in Table 2. A direct comparison of the effect of hfac and acac on complexes [Dy(hfac)3(phendione)] [36] and [Dy(acac)3(phendione)] (2) shows the same trend as indicated in the Section 1. It can be seen from Table 2 that the energy barriers Ueff of the previously studied complexes lie in the range of 29–130 cm−1, and the complex with the dppz ligand has the highest barrier. Our complex 2 has a barrier that is close to this highest reported barrier, while the barrier for complex 1 proves to be higher than the barriers for all complexes reported to date.

2.3. Quantum Chemical Calculations

The ab initio quantum chemical calculations have been performed on the electronic structure of isolated Dy(III) complexes with X-ray geometry using the OpenMolcas [37,38] without including a weak intermolecular interaction between Dy(III) ions. The eight lowest Kramers doublets (KDs) and g-tensors calculated for 1 and 2 using CASSCF/RASSI approach are summarized in Table 3.
The calculated effective gz components of g-tensors are 19.438 and 19.138 for ground KD of 1 and 2, respectively, which are close to the Ising-limit value of 20 for a pure MJ = 15/2 ground state; thus, both complexes have significant axial anisotropy for Dy(III) centers. The ground state wave functions of complex 1 (93%|±15/2>) and 2 (87%|±15/2>) show the dominant contributions of the uniaxial magnetic anisotropy of the Dy(III) ions (Table S8), which is typical for phenanthroline based β-diketonate Dy(III) complexes [10,24,36,39,40,41]. It should be noted that for complex 1, the contribution of the main component|±15/2> is somewhat higher and the ground KD in 1 is purer than in 2 in the sense that it contains a smaller number of contributions of different |MJ> states (Table 3 and Table S8). The axial character of the magnetic anisotropy tensor of the ground KDs with close gz values for Dy(III) ions in both complexes leads to the similarity of DC magnetic data (Figure 4).
The effective barriers 198 and 124 cm−1 (Table 1) of the thermally assisted Orbach relaxation mechanism extracted from AC magnetic measurements are in good agreement with the energy gaps between the ground and second excitation states 206.4 cm−1 for 1 and the gap between the ground and first excitation states 115.1 cm−1 for 2 (Table 3).
Magnetic relaxation pathways can be estimated on the basis of transition magnetic moments (Figure 7). The matrix elements of the transition magnetic moments suggest the probability of transition between two different states of the molecules [42]. The comparison of two calculated magnetic relaxation pathways confirms some difference in the dynamic magnetic properties for both complexes. The non-diagonal items of the transverse magnetic moments between ground and second excited states (0.12 μB for 1 and 0.052 μB for 2) show that the Orbach mechanism between these states is more preferable for 1 while for complex 2 the Orbach relaxation proceeds through the first excited state. Additionally, note that the matrix elements of the transition magnetic moments for TA-QTM processes in 1 are larger than in 2 (red arrows on Figure 7). This is in good agreement with the τQTM times determined from AC magnetic measurements. It can be assumed, that the main channel for QTM in 1 is TA-QTM through first and second excited states.
The directions of the principal magnetic axes in 1 and 2 do not coincide with the 4-fold axes in SAP and with each other (see Figure 8). The easy axis in 1 is almost parallel to the bond with the closest oxygen atom of one acac− ligand. It seems to be a typical axis direction in Dy based complexes [20,43,44]. In contrast, the easy axis in 2 is almost parallel to the Dy–N bond of phendione ligand. It should be noted that, in both complexes, the charges on donor atoms, according to the LoProp analysis [45], are almost the same and equal to ~−0.34e for N and ~−0.75e for O atoms.

3. Conclusions

Two mononuclear complexes [Dy(acac)3(dmdophen)] (1) and [Dy(acac)3(phendione)]·CH3CN (2) were obtained and structurally and magnetically characterized. Auxiliary neutral ligands dmdophen and phendione differ just in the peripheral substituents. The Dy(III) ions in both complexes display similar N2O6 eight-coordinate environment with square-antiprism geometry. Both 1 and 2 show SMMs properties at zero applied DC field. Relaxation at zero DC field includes two temperature-dependent processes, Orbach and Raman, and temperature-independent one, QTM. At 1000 Oe applied DC field the QTM process is completely suppressed, and the relaxation is described by the combination of the Raman and Orbach processes. The effective barriers for the thermally assisted Orbach relaxation mechanism determined from the AC magnetic measurements (198 and 124 cm−1 for 1 and 2, respectively) are in good agreement with the ab initio calculated energy gap 206.4 cm−1 between the ground and the second excited level for 1 and the gap 115.1 cm−1 between the ground and the first excited level for 2. This result clearly shows that even small structural effects of neutral ligands can play an important role in increasing the value of the spin reversal barrier.

4. Experimental Details

4.1. Materials and Methods

All chemicals were purchased from commercial sources unless otherwise noted. Elemental analysis (C, H and N) was performed on a Vario EL cube (Elementar GmbH) elemental analyzer. 1H NMR spectrum was recorded with a Bruker Avance III 500 MHz BioSpin spectrometer using the deuterated solvent signal as a lock. The FT-IR spectrum of microcrystalline powder was recorded on a Bruker ALPHA spectrometer with the ATR (attenuated total reflectance) module. Powder X-ray diffraction studies were performed on an Aeris (Malvern PANalytical B.V.) X-ray diffractometer.

4.2. Synthesis

Ligand 1,10-Phenanthroline-5,6-dione, (phendione, 4) is commercially available.
Ligand 2,2-Dimethyl-1,3-dioxolo[4,5-f][1,10]phenanthroline, (dmdophen, 3) was synthesized according to [46,47]. Additionally, 1H-NMR (500 MHz, CDCl3, 296K): δ = 9.06 (dd, 2H, J = 4.3 Hz and 1.7 Hz), 8.24 (dd, 2H, J = 8.2 Hz and 1.7 Hz), 7.59 (dd, 2H, J = 8.2 Hz and 4.3 Hz), 1.85(s, 6H) ppm. Anal. Calcd (%) for C15H12N2O2·0.5H2O (261.28 g/mol): C 68.95, H 5.02, N 10.72; found: C 69.58, H 4.98, N 10.51. FT-IR spectrum is depicted in Figure S1.
Complex [Dy(acac)3(H2O)2]·H2O (5) was obtained according to the previously reported procedure [48] with slight modifications.
Ten % water solution of ammonia (0.55 mL, 1.5 mmol) was dropwise added under intense stirring to solution of Dy(NO3)3∙5H2O (219.3 mg, 0.5 mmol) and acetylacetone (0.154 mL, 1.5 mmol) in water-ethanol mixture. White precipitate was filtered off and thoroughly washed with water. Yield 174 mg (67.7%). Anal. Calcd (%) for C15H27O9Dy (513.87 g/mol): C 35.06, H 5.29; found: C 35.07, H 5.04. FT-IR spectrum is depicted on Figures S1 and S2.

4.2.1. Synthesis of [Dy(acac)3(dmdophen)] (1)

Acetonitrile solution (2.5 mL) of 5 (51.4 mg, 0.1 mmol) and dmdophen 3 (26.1 mg, 0.1 mmol) was left for slow evaporation of the solvent. Yellow powder formed for a few days. Yield 50.7 mg (71.2%). Anal. Calcd (%) for C30H33N2O8Dy (712.10 g/mol): C 50.60, H 4.67, N 3.93; found: C 50.82, H 4.97, N 4.01. FT-IR spectrum is depicted in Figure S1. As follows from the powder XRD measurements, the sample is a monophase crystalline material (Figure S3). Single crystals were obtained by recrystallization from ethanol.

4.2.2. Synthesis of [Dy(acac)3(phendione)]·CH3CN (2)

Warm acetonitrile solution (2 mL) of phendione 4 (21.0 mg, 0.1 mmol) was added to a solution of 5 (51.4 mg, 0.1 mmol) in 1.5 mL of acetonitrile. X-ray quality orange crystals were formed upon leaving the mixture undisturbed. Yield 49.6 mg (69.8%). Anal. Calcd (%) for C29H30N3O8Dy (711.07 g/mol): C 48.99, H 4.25, N 5.91; found: C 49.36, H 4.57, N 6.13. FT-IR spectrum is depicted in Figure S2. As follows from the powder XRD measurements, the sample is a monophase crystalline material (Figure S4). Freshly obtained powder was used for magnetic measurements, because the release of the acetonitrile solvate molecule is observed.

4.3. X-ray Data Collection and Structure Refinement

X-ray data for a single crystal of 1 (at 100 K) and 2 (at 150 K) were collected on a CCD diffractometer Agilent XCalibur with EOS detector (Agilent Technologies UK Ltd., Yarnton, Oxfordshire, UK) using graphite-monochromated MoKα radiation (λ = 0.71073 Å). The structure was solved by direct methods and refined against all F2 data (SHELXTL [49]). All non-hydrogen atoms were refined with anisotropic thermal parameters, positions of hydrogen atoms were calculated and refined with riding model constraints. The X-ray crystal structure data have been deposited with the Cambridge Crystallographic Data Center, with reference codes CCDC 2211014 and 2211015. Selected crystallographic parameters and the data collection and refinement statistics are given in Table S1.
The crystalline structure of 2 involves acetonitrile (the solvent) molecule, which is weakly bound with the surrounding molecules and thus easily leaves the crystal destroying it. It is impossible to determine hydrogen atoms at the terminal carbon atom of the solvent molecule using the difference synthesis, as well as to unambiguously calculate them geometrically. The crystalline structure could not be refined with high accuracy, which results in arising level B alerts in the checkcif report.

4.4. Magnetic Measurements

DC and AC magnetic properties of powdered samples of 1 and 2 were measured at a vibrating sample magnetometer of a Cryogen Free Measurement System (Cryogenic Ltd., London, UK). The temperature dependences of the magnetic moment M(T) were measured upon cooling at T = 2–300 K in static magnetic field H = 5000 Oe. The temperature change rate was 2 K/min. The field dependences of the magnetic moment M(H) for both complexes were recorded at temperatures 2, 4, and 6 K in the field range of 0–50,000 Oe. The field change rate was 1000 Oe/min.
The measurements were carried out on polycrystalline samples moistened with mineral oil to prevent the crystals orientation in DC magnetic field. The prepared samples were sealed in plastic bags. The magnetic susceptibility χ was determined taking into account the diamagnetic contribution of the substance, using the Pascal scheme, and the bag and mineral oil contribution.
The AC measurements for 2 were carried out in 4 Oe oscillating field in the absence and with the application of DC magnetic field H = 1000 Oe. The AC magnetic behavior for 1 was studied using the Quantum Design PPMS-9 physical property measuring system with the option of measuring dynamic (AC) and static (DC) magnetic susceptibility. During AC susceptibility measurements, an alternating magnetic field amplitude was Hac = 1–5 Oe in the frequency range of 10,000–10 Hz. The relaxation time τ was extracted at each temperature using the Debye model to fit simultaneously the frequency dependence of the out-of-phase χM″ and of the in-phase susceptibility χM′.

4.5. Computational Details

The ab initio calculations have been performed using OpenMolcas program [37,38]. The [.ANO-RCC∆8s7p5d3f2g1h.] basis set for Dy atom, [.ANO-RCC∆3s2p1d.] for N and O atoms, [.ANO-RCC∆3s2p.] for C atoms and [.ANO-RCC∆2s.] for H atoms have been employed. The ground state f-electron configuration for Dy(III) is 4f9 having 6H15/2multiplet as the ground state. Initially, we have generated the guess orbitals from seven Dy(III) based starting orbitals to perform the CASSCF calculations, with 9 electrons being in 7 active orbitals with an active space of CAS (9,7). Using this active space, 21 sextets, 224 quartets and 490 doublets have been computed using the configuration interaction (CI) procedure. Then, all these 21 sextets, all 224 quartets and 98 doublets have been mixed to compute the spin-orbit states using RASSI-SO module. After computing these spin-orbit states, the corresponding g-tensors and CF parameters for eight low-lying Kramers doublets (KD) have been extracted using SINGLE_ANISO code [50]. The Cholesky decomposition for two electron integrals has been employed throughout the calculations to reduce the disk space.

Supplementary Materials

The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/magnetochemistry8110151/s1, FT-IR spectra for 1, 2, dmdophen (3), phendione (4) and [Dy(acac)3(H2O)2]·H2O (5) (Figures S1 and S2); powder X-ray diffraction patterns of polycrystalline sample for 1 and 2 (Figures S3 and S4); crystal data and structure refinement for 1 and 2 (Table S1); selected bond lengths and angles for 1 and 2 (Table S2); the local symmetry of Dy(III) ion for 1 and 2 defined by the continuous shape measure (CShM) analysis with SHAPE software (Table S3); short intra- and intermolecular contacts in crystal pacing of 1 and 2 (Figure S5); frequency dependences of the in-phase (a) and out-of-phase (b) AC susceptibility, Cole-Cole plots (c) for 1 at zero DC field and temperatures from 2 to 20 K (Figure S6); Frequency dependences of the in-phase (a) and out-of-phase (b) AC susceptibility, Cole-Cole plots (c) for 1 at 10 K and DC fields 0–5000 Oe (Figure S7); field dependence of the inverse relaxation time τ−1 for 1 at 10 K (Figure S8); frequency dependences of the in-phase AC susceptibility (a) and Cole-Cole plots (b) for 1 at 1000 Oe DC field and temperatures from 8 to 20 K (Figure S9); frequency dependences of the in-phase (a) and out-of-phase (b) AC susceptibility, Cole-Cole plots (c) for 2 at zero DC field and temperatures from 2 to 20 K (Figure S10); frequency dependences of the in-phase (a) and out-of-phase (b) AC susceptibility, Cole-Cole plots (c) for 2 at 10 K and DC fields 0–5000 Oe (Figure S11); field dependence of the inverse relaxation time τ−1 for 2 at 10 K (Figure S12); frequency dependences of the in-phase (a) and out-of-phase (b) AC susceptibility, Cole-Cole plots (c) for 2 at DC field 1000 Oe and temperatures from 8 to 20 K (Figure S13); best fit parameters for 1 and 2 at zero and 1000 Oe DC fields (Tables S4–S7); SINGLE_ANISO computed wave function decomposition analysis for lowest KDs of Dy(III) ions in 1 and 2 (Table S8).

Author Contributions

Synthesis, E.V.G.; X-ray analysis and structure refinement, G.V.S.; ab initio calculations D.V.K.; DC and AC magnetic measurements, M.V.Z., A.I.D. and N.N.E.; AC magnetic measurements analysis and conceptualization, E.A.Y.; writing—the original draft preparation, E.A.Y. and D.V.K.; writing—review and editing, D.V.K., A.V.P., E.A.Y. and S.M.A.; supervision, A.V.P. and S.M.A.; project administration, S.M.A.; funding acquisition, S.M.A. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Science and Higher Education of the Russian Federation, grant number 075-15-2020-779.

Informed Consent Statement

Not applicable.

Acknowledgments

The APC was funded by MDPI-Magnetochemistry. Elemental and NMR analyses were performed using the equipment of the Multi-user Analytical Center of FRC PCP MC RAS. The research was partially performed using the equipment of the JRC PMR IGIC RAS.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Zabala-Lekuona, A.; Seco, J.M.; Colacio, E. Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time. Coord. Chem. Rev. 2021, 441, 213984. [Google Scholar] [CrossRef]
  2. Gebrezgiabher, M.; Bayeh, Y.; Gebretsadik, T.; Gebreslassie, G.; Elemo, F.; Thomas, M.; Linert, W. Lanthanide-Based Single-Molecule Magnets Derived from Schiff Base Ligands of Salicylaldehyde Derivatives. Inorganics 2020, 8, 66. [Google Scholar] [CrossRef]
  3. Perlepe, P.S.; Maniaki, D.; Pilichos, E.; Katsoulakou, E.; Perlepes, S.P. Smart Ligands for Efficient 3d-, 4d- and 5d-Metal Single-Molecule Magnets and Single-Ion Magnets. Inorganics 2020, 8, 39. [Google Scholar] [CrossRef]
  4. Baldoví, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Palii, A. Rational Design of Single-Ion Magnets and Spin Qubits Based on Mononuclear Lanthanoid Complexes. Inorg. Chem. 2012, 51, 12565–12574. [Google Scholar] [CrossRef]
  5. Aldoshin, S.M.; Korchagin, D.V.; Palii, A.V.; Tsukerblat, B.S. Some new trends in the design of single molecule magnets. Pure Appl. Chem. 2017, 89, 1119–1143. [Google Scholar] [CrossRef]
  6. Zhang, P.; Yun-Nan, G.; Jinkui, T. Recent advances in dysprosium-based single molecule magnets: Structural overview and synthetic strategies. Coord. Chem. Rev. 2013, 257, 1728–1763. [Google Scholar] [CrossRef]
  7. Dey, A.; Kalita, P.; Chandrasekhar, V. Lanthanide(III)-Based Single-Ion Magnets. ACS Omega 2018, 3, 9462–9475. [Google Scholar] [CrossRef]
  8. Blachowicz, T.; Ehrmann, A. New Materials and Effects in Molecular Nanomagnets. Appl. Sci. 2021, 11, 7510. [Google Scholar] [CrossRef]
  9. Bazhenova, T.A.; Kopotkov, V.A.; Korchagin, D.V.; Manakin, Y.V.; Zorina, L.V.; Simonov, S.V.; Yakushev, I.A.; Mironov, V.S.; Vasiliev, A.N.; Maximova, O.V.; et al. A Series of Novel Pentagonal-Bipyramidal Erbium(III) Complexes with Acyclic Chelating N3O2 Schiff-Base Ligands: Synthesis, Structure, and Magnetism. Molecules 2021, 26, 6908. [Google Scholar] [CrossRef]
  10. Zhang, S.; Mo, W.; Zhang, J.; Zhang, Z.; Yin, B.; Hu, D.; Chen, S. Regulation of Substituent Effects on Configurations and Magnetic Performances of Mononuclear DyIII Single-Molecule Magnets. Inorg. Chem. 2019, 58, 15330–15343. [Google Scholar] [CrossRef]
  11. Shao, D.; Yang, J.; Yang, X.; Tian, Z. An Azido-Bridged Dysprosium Chain Complex Showing Zero-field Slow Magnetic Relaxation. Chem Asian J. 2021, 16, 3331–3335. [Google Scholar] [CrossRef]
  12. Shao, D.; Tang, W.-J.; Ruan, Z.; Yang, X.; Shi, L.; Wei, X.-Q.; Tian, Z.; Kumari, K.; Singh, S.K. Water-driven reversible switching of single-ion magnetism and proton conduction in a dysprosium sulfonate. Inorg. Chem. Front. 2022. [Google Scholar] [CrossRef]
  13. Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Cryst. B 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
  14. Tong, Y.Z.; Gao, C.; Wang, Q.-L.; Wang, B.-W.; Gao, S.; Cheng, P.; Liao, D.-Z. Two mononuclear single molecule magnets derived from dysprosium(iii) and tmphen (tmphen = 3,4,7,8-tetramethyl-1,10-phenanthroline). Dalton Trans. 2015, 44, 9020–9026. [Google Scholar] [CrossRef]
  15. Guo, M.; Wu, J.; Cador, O.; Lu, J.; Yin, B.; Le Guennic, B.; Tang, J. Manipulating the Relaxation of Quasi-D4d Dysprosium Compounds through Alternation of the O-Donor Ligands. Inorg. Chem. 2018, 57, 4534–4542. [Google Scholar] [CrossRef]
  16. Chen, G.-J.; Gao, C.-Y.; Tian, J.-L.; Tang, J.; Gu, W.; Liu, X.; Yan, S.-P.; Liao, D.-Z.; Cheng, P. Coordination-perturbed single-molecule magnet behaviour of mononuclear dysprosium complexes. Dalton Trans. 2011, 40, 5579–5583. [Google Scholar] [CrossRef] [PubMed]
  17. Chen, G.-J.; Guo, Y.-N.; Tian, J.-L.; Tang, J.; Gu, W.; Liu, X.; Yan, S.-P.; Cheng, P.; Liao, D.-Z. Enhancing Anisotropy Barriers of Dysprosium(III) Single-Ion Magnets. Chem. Eur. J. 2012, 18, 2484–2487. [Google Scholar] [CrossRef]
  18. Chen, G.-J.; Zhou, Y.; Jin, G.-X.; Dong, Y.-B. [Dy(acac)3(dppn)]·C2H5OH: Construction of a single-ion magnet based on the square-antiprism dysprosium(III) ion. Dalton Trans. 2014, 43, 16659–16665. [Google Scholar] [CrossRef] [PubMed]
  19. Aravena, D.; Ruiz, E. Shedding Light on the Single-Molecule Magnet Behavior of Mononuclear DyIII Complexes. Inorg. Chem. 2013, 52, 13770–13778. [Google Scholar] [CrossRef] [PubMed]
  20. Chilton, N.F.; Collison, D.; McInnes, E.J.L.; Winpenny, R.E.P.; Soncini, A. An electrostatic model for the determination of magnetic anisotropy in dysprosium complexes. Nat. Commun. 2013, 4, 2551. [Google Scholar] [CrossRef] [Green Version]
  21. Yao, X.; Yan, P.; An, G.; Shi, C.; Li, Y.; Li, G. Single-ion magnets with D4d symmetry based on electron-donating β-diketonate Dy(III) complexes. New J. Chem. 2018, 42, 8438–8444. [Google Scholar] [CrossRef]
  22. Bi , Y.; Guo, Y.-N.; Zhao, L.; Guo, Y.; Lin, S.-Y.; Jiang, S.-D.; Tang, J.; Wang, B.-W.; Gao, S. Capping Ligand Perturbed Slow Magnetic Relaxation in Dysprosium Single-Ion Magnets. Chem. Eur. J. 2011, 17, 12476–12481. [Google Scholar] [CrossRef]
  23. Wang, Y.-L.; Ma, Y.; Yang, X.; Tang, J.; Cheng, P.; Wang, Q.-L.; Li, L.-C.; Liao, D.-Z. Syntheses, Structures, and Magnetic and Luminescence Properties of a New DyIII-Based Single-Ion Magnet. Inorg. Chem. 2013, 52, 7380–7386. [Google Scholar] [CrossRef]
  24. Cen, P.; Liu, X.; Ferrando-Soria, J.; Zhang, Y.-Q.; Xie, G.; Chen, S.; Pardo, E. Capping N-Donor Ligands Modulate the Magnetic Dynamics of DyIII β-Diketonate Single-Ion Magnets with D4d Symmetry. Chem. Eur. J. 2019, 25, 3884–3892. [Google Scholar] [CrossRef] [PubMed]
  25. Cen, P.; Wang, M.; Ma, X.; Chen, L.; Zhang, Y.-Q.; Li, Y.; Tian, D.; Liu, X. Coordination microenvironment perturbed single-ion magnet behavior in a β-diketone Dy(III) complex. CrystEngComm 2020, 22, 6856–6863. [Google Scholar] [CrossRef]
  26. Llunell, M.; Casanova, D.; Cirera, J.; Alemany, P.; Alvarez, S. SHAPE. version 2.1. 2013. [Google Scholar]
  27. Casanova, D.; Llunell, M.; Alemany, P.; Alvarez, S. The rich stereochemistry of eight-vertex polyhedra: A continuous shape measures study. Chem. Eur. J. 2005, 11, 1479–1494. [Google Scholar] [CrossRef]
  28. AlDamen, M.A.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Martí-Gastaldo, C.; Luis, F.; Montero, O. Mononuclear Lanthanide Single Molecule Magnets Based on the Polyoxometalates [Ln(W5O18)2]9− and [Ln(β2-SiW11O39)2]13− (LnIII = Tb, Dy, Ho, Er, Tm, and Yb). Inorg. Chem. 2009, 48, 3467–3479. [Google Scholar] [CrossRef]
  29. Sorace, L.; Benelli, C.; Gatteschi, D. Lanthanides in molecular magnetism: Old tools in a new field. Chem. Soc. Rev. 2011, 40, 3092–3104. [Google Scholar] [CrossRef]
  30. Yureva, E.A.; Korchagin, D.V.; Anichkin, A.A.; Shilov, G.V.; Babeshkin, K.A.; Efimov, N.N.; Palii, A.V.; Aldoshin, S.M. Evidence for zero-field slow magnetic relaxation in a Co(ii) complex with a pseudo-tetrahedral N2I2 environment. Dalton Trans. 2022, 51, 11916–11921. [Google Scholar] [CrossRef]
  31. Gavrikov, A.V.; Koroteev, P.S.; Efimov, N.N.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Kostopoulos, A.K.; Ariciu, A.-M.; Novotortsev, V.M. Novel mononuclear and 1D-polymeric derivatives of lanthanides and (η 6-benzoic acid)tricarbonylchromium: Synthesis, structure and magnetism. Dalton Trans. 2017, 46, 3369–3380. [Google Scholar] [CrossRef] [PubMed]
  32. Gavrikov, A.V.; Efimov, N.N.; Dobrokhotova, Z.V.; Ilyukhin, A.B.; Vasilyev, P.N.; Novotortsev, V.M. Novel mononuclear Ln complexes with pyrazine-2-carboxylate and acetylacetonate co-ligands: Remarkable single molecule magnet behavior of a Yb derivative. Dalton Trans. 2017, 46, 11806–11816. [Google Scholar] [CrossRef] [PubMed]
  33. Zhang, S.; Mo, W.J.; Yin, B.; Zhang, G.N.; Yang, D.S.; Lü, X.Q.; Chen, S.P. The slow magnetic relaxation regulated by the coordination, configuration and intermolecular dipolar field in two mononuclear DyIII single-molecule magnets (SMMs). Dalton Trans. 2018, 47, 12393–12405. [Google Scholar] [CrossRef] [PubMed]
  34. Jiang, S.-D.; Wang, B.-W.; Su, G.; Wang, Z.-M.; Gao, S. A Mononuclear Dysprosium Complex Featuring Single-Molecule-Magnet Behavior. Angew. Chem. Int. Ed. 2010, 49, 7448–7451. [Google Scholar] [CrossRef]
  35. Habib, F.; Lin, P.-H.; Long, J.; Korobkov, I.; Wernsdorfer, W.; Murugesu, M. The Use of Magnetic Dilution to Elucidate the Slow Magnetic Relaxation Effects of a Dy2 Single-Molecule Magnet. J. Am. Chem. Soc. 2011, 133, 8830–8833. [Google Scholar] [CrossRef]
  36. Galangau, O.; Flores Gonzalez, J.; Montigaud, V.; Dorcet, V.; le Guennic, B.; Cador, O.; Pointillart, F. Dysprosium Single-Molecule Magnets Involving 1,10-Phenantroline-5,6-dione Ligand. Magnetochemistry 2020, 6, 19. [Google Scholar] [CrossRef] [Green Version]
  37. Galván, I.F.; Vacher, M.; Alavi, A.; Angeli, C.; Aquilante, F.; Autschbach, J.; Bao, J.J.; Bokarev, S.I.; Bogdanov, N.A.; Carlson, R.K.; et al. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef]
  38. Aquilante, F.; Autschbach, J.; Baiardi, A.; Battaglia, S.; Borin, V.A.; Chibotaru, L.F.; Conti, I.; De Vico, L.; Delcey, M.; Galván, I.F.; et al. Modern quantum chemistry with [Open]Molcas. J. Chem. Phys. 2020, 152, 214117. [Google Scholar] [CrossRef]
  39. Kong, M.; Feng, X.; Li, J.; Hu, Z.-B.; Wang, J.; Song, X.-J.; Jing, Z.-Y.; Zhang, Y.-Q.; Song, Y. Structurally modulated single-ion magnets of mononuclear β-diketone dysprosium(III) complexes. Dalton Trans. 2020, 49, 14931–14940. [Google Scholar] [CrossRef]
  40. Xi, J.; Ma, X.; Cen, P.; Wu, Y.; Zhang, Y.-Q.; Guo, Y.; Yang, J.; Chen, L.; Liu, X. Regulating the magnetic dynamics of mononuclear β-diketone Dy(III) single-molecule magnets through the substitution effect on capping N-donor coligands. Dalton Trans. 2021, 50, 2102–2111. [Google Scholar] [CrossRef]
  41. Cen, P.-P.; Zhang, S.; Liu, X.-Y.; Song, W.-M.; Zhang, Y.-Q.; Xie, G.; Chen, S.-P. Electrostatic Potential Determined Magnetic Dynamics Observed in Two Mononuclear β-Diketone Dysprosium(III) Single-Molecule Magnets. Inorg. Chem. 2017, 56, 3644–3656. [Google Scholar] [CrossRef] [PubMed]
  42. Ungur, L.; Chibotaru, L. Strategies toward High-Temperature Lanthanide-Based Single-Molecule Magnets. Inorg. Chem. 2016, 556, 10043–10056. [Google Scholar] [CrossRef] [PubMed]
  43. Ding, Y.-S.; Han, T.; Zhai, Y.-Q.; Reta, D.; Chilton, N.F.; Winpenny, R.E.P.; Zheng, Y.-Z. A Study of Magnetic Relaxation in Dysprosium(III) Single Molecule Magnets. Chem. Eur. J. 2020, 26, 5893–5902. [Google Scholar] [CrossRef] [PubMed]
  44. Briganti, M.; Santanni, F.; Tesi, L.; Totti, F.; Sessoli, R.; Lunghi, A. A Complete Ab Initio View of Orbach and Raman Spin–Lattice Relaxation in a Dysprosium Coordination Compound. J. Am. Chem. Soc. 2021, 143, 13633–13645. [Google Scholar] [CrossRef] [PubMed]
  45. Gagliardi, L.; Lindh, R.; Karlstrom, G. Local properties of quantum chemical systems: The LoProp approach. J. Chem. Phys. 2004, 121, 4494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  46. Pfeffer, M.G.; Zedler, L.; Kupfer, S.; Paul, M.; Schwalbe, M.; Peuntinger, K.; Guldi, D.M.; Guthmuller, J.; Popp, J.; Graefe, S.; et al. Tuning of photocatalytic activity by creating a tridentate coordination sphere for palladium. Dalton Trans. 2014, 43, 11676–11686. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  47. Frey, J.; Kraus, T.; Heitz, V.; Sauvage, J.-P. Synthesis of a bis-macrocycle containing two back-to-back rigidly connected 1,10-phenanthroline units as a central core and its incorporation in a handcuff-like catenane. Chem. Eur. J. 2007, 13, 7584–7594. [Google Scholar] [CrossRef]
  48. Voloshin, A.I.; Shavaleev, N.M.; Kazakov, V.P. Chemiluminescence of praseodymium (III), neodymium (III) and ytterbium (III) β-diketonates in solution excited from 1,2-dioxetane decomposition and singlet-singlet energy transfer from ketone to rare-earth β-diketonates. J. Luminescence 2000, 91, 49–58. [Google Scholar] [CrossRef]
  49. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Cryst. C 2015, 71, 3–8. [Google Scholar] [CrossRef] [Green Version]
  50. Chibotaru, L.F.; Ungur, L. Ab initio calculation of anisotropic magnetic properties of complexes. I. Unique definition of pseudospin Hamiltonians and their derivation. J. Chem. Phys. 2012, 137, 064112. [Google Scholar] [CrossRef]
Magnetochemistry 08 00151 g001 550
Figure 1. Chemical structures of complexes 1 and 2.
Figure 1. Chemical structures of complexes 1 and 2.
Magnetochemistry 08 00151 g001
Magnetochemistry 08 00151 g002 550
Figure 2. Molecular structures of 1 (a) and 2 (b). Hydrogen atoms are omitted for clarity.
Figure 2. Molecular structures of 1 (a) and 2 (b). Hydrogen atoms are omitted for clarity.
Magnetochemistry 08 00151 g002
Magnetochemistry 08 00151 g003 550
Figure 3. Schematic structure of square-antiprismatic (SAP) geometry (a). Relevant angular parameters in SAP geometry: Φ (b), the angle between the diagonals of the two squares (skew angle); α (c), the angle between the S8 axis and the Dy–O/N vector. For the highest SAP symmetry Φ = 45° and α = 54.74°.
Figure 3. Schematic structure of square-antiprismatic (SAP) geometry (a). Relevant angular parameters in SAP geometry: Φ (b), the angle between the diagonals of the two squares (skew angle); α (c), the angle between the S8 axis and the Dy–O/N vector. For the highest SAP symmetry Φ = 45° and α = 54.74°.
Magnetochemistry 08 00151 g003
Magnetochemistry 08 00151 g004 550
Figure 4. Temperature dependences of χMT for 1 (a) and 2 (b). Insets: magnetization vs. field plots at different temperatures (2, 4 and 6 K). The red solid lines show the corresponding results of the SA-CASSCF/SO-RASSI/SINGLE_ANISO calculations.
Figure 4. Temperature dependences of χMT for 1 (a) and 2 (b). Insets: magnetization vs. field plots at different temperatures (2, 4 and 6 K). The red solid lines show the corresponding results of the SA-CASSCF/SO-RASSI/SINGLE_ANISO calculations.
Magnetochemistry 08 00151 g004
Magnetochemistry 08 00151 g005 550
Figure 5. Frequency dependences of the out-of-phase AC susceptibility for 1 (left) and 2 (right) at zero (a,b) and 1000 Oe DC field (c,d). Temperatures are shown in increments of 2 K.
Figure 5. Frequency dependences of the out-of-phase AC susceptibility for 1 (left) and 2 (right) at zero (a,b) and 1000 Oe DC field (c,d). Temperatures are shown in increments of 2 K.
Magnetochemistry 08 00151 g005
Magnetochemistry 08 00151 g006 550
Figure 6. Temperature dependences of the relaxation times τ for 1 (a) and 2 (b) at zero (black) and 1000 Oe (red) DC field. Solid lines are the theoretical curves obtained with the best-fit parameters given in Table 1.
Figure 6. Temperature dependences of the relaxation times τ for 1 (a) and 2 (b) at zero (black) and 1000 Oe (red) DC field. Solid lines are the theoretical curves obtained with the best-fit parameters given in Table 1.
Magnetochemistry 08 00151 g006
Magnetochemistry 08 00151 g007 550
Figure 7. Computed possible magnetization relaxation pathways for 1 (a) and 2 (b). The red arrows show QTM and TA-QTM via ground and higher excited KD, respectively. The blue arrows show the Orbach process for the relaxation. The green arrows show the mechanism of magnetic relaxation.
Figure 7. Computed possible magnetization relaxation pathways for 1 (a) and 2 (b). The red arrows show QTM and TA-QTM via ground and higher excited KD, respectively. The blue arrows show the Orbach process for the relaxation. The green arrows show the mechanism of magnetic relaxation.
Magnetochemistry 08 00151 g007
Magnetochemistry 08 00151 g008 550
Figure 8. The molecular structures of 1 (a) and 2 (b) together with the easy axis (magenta) of ground KD obtained within the ab initio SA-CASSCF/RASSI-SO/SINGLE_ANISO calculation. Color code: red = oxygen, blue = nitrogen, gray = carbon, white = hydrogen.
Figure 8. The molecular structures of 1 (a) and 2 (b) together with the easy axis (magenta) of ground KD obtained within the ab initio SA-CASSCF/RASSI-SO/SINGLE_ANISO calculation. Color code: red = oxygen, blue = nitrogen, gray = carbon, white = hydrogen.
Magnetochemistry 08 00151 g008
Table
Table 2. The energy barriers (Ueff) for complexes of general formula [DyIII(acac)3(L)] with bidentate ligand L.
Table 2. The energy barriers (Ueff) for complexes of general formula [DyIII(acac)3(L)] with bidentate ligand L.
Compound 1UeffRef.
[Dy(acac)3(H2O)2]45.9 cm−1 (66.1 K)[34]
[Dy(acac)3(phen)]44.4 cm−1 (63.8 K)[16]
[Dy(acac)3(dpq)]94.5 cm−1 (136 K)[17]
[Dy(acac)3(dppz)]130 cm−1 (187 K)[17]
[Dy(acac)3(dppn)]28.9 cm−1 (37.2 K)[18]
[Dy(acac)3(tmphen)]90.9 cm−1 (130.4 K)[14]
[Dy(acac)3(lz)]112 cm−1 (162 K)[15]
[Dy(hfac)3(phendione)] 283 cm−1 (119 K)[36]
[Dy(acac)3(phendione)]124 cm−1 (178 K)This work, complex 2
[Dy(acac)3(dmdophen)]198 cm−1 (284 K)This work, complex 1
1 phen—1,10-phenanthroline; dpq—pyrazino[2,3-f][1,10]phenanthroline; dppz—dipyrido[3,2-a:2′,3′-c]phenazine; dppn—benzo[i]dipyrido[3,2-a:2′,3′-c]phenazine; tmphen—3,4,7,8-tetramethyl-1,10-phenanthroline; lz—2,4-diamino-6-pyridyl-1,3,5-triazine; phendione—1,10-phenanthroline-5,6-dione; dmdophen—2,2-dimethyl-1,3-dioxolo[4,5-f][1,10]phenanthroline. 2 this complex is added to the Table for direct comparison of hfac and acac since it has the same L ligand as complex 2.
Table
Table 3. The ab initio computed energy levels (cm−1) and associated g-tensors of the eight lowest KDs for 1 and 2.
Table 3. The ab initio computed energy levels (cm−1) and associated g-tensors of the eight lowest KDs for 1 and 2.
KD12
EnergygxgygzEnergygxgygz
10.00.0150.02219.4380.00.0110.01619.138
2130.50.5140.78915.862115.10.1910.25515.601
3206.42.3164.45210.287184.50.1980.37312.578
4236.52.8595.48810.271224.34.4896.2628.314
5279.51.2621.54313.633263.72.7173.34812.569
6328.60.0570.07918.791313.40.5370.74618.581
7420.50.0750.11619.206402.60.0270.05719.047
8563.10.0140.02919.693546.30.0050.01119.703
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Gorshkov, E.V.; Korchagin, D.V.; Yureva, E.A.; Shilov, G.V.; Zhidkov, M.V.; Dmitriev, A.I.; Efimov, N.N.; Palii, A.V.; Aldoshin, S.M. Effect of Ligand Substitution on Zero-Field Slow Magnetic Relaxation in Mononuclear Dy(III) β-Diketonate Complexes with Phenanthroline-Based Ligands. Magnetochemistry 2022, 8, 151. https://doi.org/10.3390/magnetochemistry8110151

AMA Style

Gorshkov EV, Korchagin DV, Yureva EA, Shilov GV, Zhidkov MV, Dmitriev AI, Efimov NN, Palii AV, Aldoshin SM. Effect of Ligand Substitution on Zero-Field Slow Magnetic Relaxation in Mononuclear Dy(III) β-Diketonate Complexes with Phenanthroline-Based Ligands. Magnetochemistry. 2022; 8(11):151. https://doi.org/10.3390/magnetochemistry8110151

Chicago/Turabian Style

Gorshkov, Egor V., Denis V. Korchagin, Elena A. Yureva, Gennadii V. Shilov, Mikhail V. Zhidkov, Alexei I. Dmitriev, Nikolay N. Efimov, Andrew V. Palii, and Sergey M. Aldoshin. 2022. "Effect of Ligand Substitution on Zero-Field Slow Magnetic Relaxation in Mononuclear Dy(III) β-Diketonate Complexes with Phenanthroline-Based Ligands" Magnetochemistry 8, no. 11: 151. https://doi.org/10.3390/magnetochemistry8110151

APA Style

Gorshkov, E. V., Korchagin, D. V., Yureva, E. A., Shilov, G. V., Zhidkov, M. V., Dmitriev, A. I., Efimov, N. N., Palii, A. V., & Aldoshin, S. M. (2022). Effect of Ligand Substitution on Zero-Field Slow Magnetic Relaxation in Mononuclear Dy(III) β-Diketonate Complexes with Phenanthroline-Based Ligands. Magnetochemistry, 8(11), 151. https://doi.org/10.3390/magnetochemistry8110151

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop