Comparison of Electronic Resistance Measurement Methods and Influencing Parameters for LMFP and High-Nickel NCM Cathodes

Abstract

The automotive industry aims for the highest possible driving range (highest energy density) in combination with a fast charge ability (highest power density) of electric vehicles. With both targets being intrinsically contradictory, it is important to understand and optimize resistances within lithium-ion battery (LIB) electrodes. In this study, the properties and magnitude of electronic resistance contributions in LiMn_0.7Fe_0.3PO₄ (LMFP)- and LiNi_xCo_yMn_zO₂ (NCM, x = 0.88~0.90, x + y + z = 1)-based electrodes are comprehensively investigated through the use of different measurement methods. Contact resistance properties are characterized via electrochemical impedance spectroscopy (EIS) on the example of LMFP cathodes. The EIS results are compared to a two-point probe as well as to the results obtained using a novel commercial 46-point probe system. The magnitude and ratio of contact resistance and compound electronic resistance for LMFP- and NCM-based cathodes are discussed on the basis of the 46-point probe measurement results. The results show that the 46-point probe yields significantly lower resistance values than those in EIS studies. Further results show that electronic resistance values in cathodes can vary over several orders of magnitude. Various influence parameters such as electrode porosity, type of current collector and the impact of solvent soaking on electronic resistance are investigated.

1. Introduction

Improving the fast charge behavior of lithium-ion battery cells is one of the main goals in science and industry. To understand how to improve a fast charge performance in the most efficient way, it is important to understand the limiting factors. Various reviews have been published on this topic [1,2,3].

The reason for low-capacity retention at high charge and discharge rates are overpotential contributions caused by various effects at the cell and electrode levels, such as charge-transfer resistance, ionic resistance and electronic resistances. In order to optimize the fast charge behavior, these bottlenecks must be analyzed, understood and overcome while also taking into consideration other LIB design goals such as high energy density and safety.

The extent of each of the resistance contributions is strongly dependent on the used active material, electrode design factors (e.g., porosity and thickness) and measurement settings (e.g., temperature and state of charge (SoC)). Various works have been published on the identification of resistance contributions in LIBs [2,4,5,6]. However, because of the various dependencies mentioned above, there is no general resistance of main importance (“limiting resistance”). It is important to gain insights on all resistance types to make electrode optimization efficient. Within this paper, we focus on the electronic resistance in LIB cathodes, which is, among others, an essential part in the electrode and LIB design process.

To investigate the impact of cathode active materials (CAMs) on electronic resistance, this study utilized two groups of CAMs: LMFP and NCM. LMFP has gained attention as a potential successor to LiFePO₄ (LFP), aiming to provide a higher energy density while maintaining good availability of cheap raw materials. Like LFP, LMFP crystallizes in the olivine crystal structure [7]. Its intrinsic electronic conductivity is generally assumed to be lower than that of LFP [8,9]. However, it was not possible to find consistent data in the literature on this topic. For example, Chung et al. [10] reported ~10⁻⁹ S∙cm⁻¹ for undoped LFP, whereas Lee et al. [11] reported ~10⁻⁵ S∙cm⁻¹ for undoped LMFP using a different measurement method. The comparison of materials is further complicated by the finding that small amounts of impurities can act as dopants, which in turn have a huge impact on the electronic conductivity [10]. The assumption of the lower electronic conductivity of LMFP powder is probably drawn from a comparison of LFP with LiMnPO₄ (LMP), in which LMP mostly shows larger band gaps and thus a lower electronic conductivity [12]. Nevertheless, real-world lithium-ion battery LMFP cathodes show low electronic conductivity, which makes them a highly interesting candidate for the tailoring of the carbon matrix inside the cathode and associated electronic conductivity studies. Due to the intrinsically low electronic conductivity, most of the commercially available LFP and LMFP materials are carbon coated.

Also, for NCM powder, electronic conductivity values are hard to find and often not comparable because of varying measurement methods. Reported values are typically in the range of 10⁻³ S∙cm⁻¹ [13,14]. This is a significantly higher electronic conductivity compared to that of LMFP.

Typically, the cathode active material (CAM) is mixed with carbonaceous conducting additives in electrode preparation to reduce the electronic resistance. However, the conductive additive itself counts as inactive material in the electrode and should therefore be minimized to achieve sufficient energy density [15]. Various studies have been performed, highlighting the impact of type (structure, dimensionality, aspect ratio, percolation properties) and amount of conductive additive in LIB cathodes [15,16,17,18]. Other studies have emphasized a strong dependence of the electronic resistance on the connection between the electrode compound and current collector [6,19,20]. These findings indicate that the electronic resistance of cathodes must depend on two very specific contributions. The first is the resistance between the current collector (CC) and electrode compound, denoted herein as R_Contact, whereas the second is the electronic resistance within the electrode compound itself, denoted herein as R_Compound.

Typical challenges in studies on electronic resistance optimization are the various dependency factors and the difficulty to correctly separate and measure the—often interdependent—electronic resistance contributions. When, for example, the goal is the reduction of R_Compound by tuning and investigating the type and amount of conductive additive, it also becomes necessary to strictly control the density to which the electrodes are compressed (electrode press density) to keep R_Contact constant, which will otherwise strongly influence the overall electronic resistance. Special attention throughout calendering is thus required.

Established methods for electronic resistance characterization include different types of two-point probes [17,18,21], impedance spectroscopy [19,20], four-point probes and probe heads designed to fulfill special measurement targets [22,23]. All of these systems have specific advantages and disadvantages:

• With the two-point probe technique, it is not possible to separate R_Contact and R_Compound. Moreover, the measured resistance usually includes an error from the contacting of the sample between the measurement heads.
• Commercially available four-point probe setups are typically short circuited if the sample is an electrode coating applied on a metallic CC due to the considerably higher conductivity of the CC. Accordingly, coatings must be applied on electrically isolating substrates, which can cause limitations in sample preparation such as reaching the desired press density via calendering. This in turn leads to data not being representative for the real application.
• EIS can be applied to measure R_Contact directly if its contribution to the resistance is large enough. However, determining R_Compound can be challenging as it is overlaid by the electrolyte resistance, as both occur as a serial resistance contribution in the high-frequency region [24].
• Recent developments are focused on the designs of advanced probe heads allowing the separation of R_Contact and R_Compound in one convenient electrical measurement within one simple measurement [22,23]. The 46-point probe device (RM2610) commercialized by the company HIOKI is working along these principles. The determination of R_Contact and R_Compound for the as-prepared, dry electrode coating applied on the CC is fast and easy, which opens up new ways to systematically study and optimize electronic resistances in battery electrodes. Still, this innovative measuring device lacks validation against established methodologies in order to prove its applicability. Also, the accuracy of the cell performance forecasted from dry electrode data is under question.

In this study, the properties and magnitude of electronic resistance contributions in LMFP- and NCM-based cathode electrodes are investigated with different measurement methods. R_Contact properties are characterized via EIS on the example of LMFP cathodes. The EIS results are compared to results obtained from classic 2-point probe and innovative 46-point probe measurements, yielding not yet reported information on the correlation of these methods. On the basis of 46-point probe data the magnitudes and ratios of the R_Contact and R_Compound for LMFP- and NCM-based cathodes are also discussed. Finally, we shed light on the interplay between electronic resistance, calendering strength (cathode press density) and particle morphology through a careful interpretation of dry electrode benchmarking results obtained using the 46-point probe device.

2. Materials and Methods

2.1. Electrode Preparation

Cathode slurries were prepared by mixing cathode active material (CAM) powders with carbon black (CB) (LITx HP, CABOT, USA), single-walled carbon nanotubes (SWCNTs) (TUBALL, OCSiAl, Luxembourg) and Polyvinylidene fluoride binder (PVDF) in battery-grade N-Methyl-2-pyrrolidon (NMP, water ≤ 300 ppm) through the use of a thinky-type mixer. The ratio of CAM/CB/SWCNT/PVDF was adjusted to obtain a CAM share of 97.04% in the cathode. Used CAMs were a carbon-coated LiMn_0.7Fe_0.3PO₄ (LMFP, D₅₀ = 14 µm), poly-crystalline NCM with 90% Nickel content (Ni90-NCM-PC, D₅₀ = 12.55 µm) and single-crystalline NCM with 88% Nickel content (Ni88-NCM-SC, D₅₀ = 3.52 µm) sourced from commercial suppliers.

The cathode slurries were cast either on a 20 µm Al-current collector (Al-CC) or on a 12 µm carbon primer coated Al-current collector (primed-CC). Coating thickness was adjusted to obtain mass loadings corresponding to an areal capacity of 3 mAh/cm² (half-cell vs. Li/Li⁺ at 0.33 C and 25 °C), if not stated otherwise. The coated electrodes were dried at 80 °C in vacuum overnight. Cathodes were then calendered at room temperature with a lab calender to desired press densities (porosities).

2.2. Electrode Tests and EIS Measurement

Impedance measurements were performed in a 3-electrode setup through the use of PAT-core cells sourced from EL-CELL with the probe cathode as a working electrode (Ø = 18 mm), a Li ring as a reference electrode and two glass fiber separators (Whatman GF/A). A graphite (Showa Denko CF-C) anode was used as the counter electrode (Ø = 18 mm). The negative-to-positive (N:P) ratio of the full cell was adjusted to 1.15. As electrolyte, 400 µL of 1.2 M LiPF₆ in a mixture of ethylene carbonate (EC), dimethyl carbonate (DMC) and ethylene methylene carbonate (EMC) (EC:DMC:EMC = 30:35:35 by volume) + 1.5 wt.% vinylene carbonate was used. Two full cycles at 0.1 C and 25 °C were performed for formation. The voltage range for the formation and cycling was 2.8–4.2 V. Specific state-of-charge (SoC) points were adjusted with a current of 1 C and subsequent rest time of 30 min before EIS measurement.

EIS measurements were carried out on a multichannel potentiostat/galvanostat (VMP-3e, Biologic, France) and following a potentiostatic impedance measurement protocol. The measurement parameters used were a 100 kHz–100 mHz frequency range, 10 mV amplitude, 2 points per frequency and 10 points per decade. The spectra were normalized to the electrode area for better comparability. The fitting of impedance spectra was conducted through the use of RelaxIS3 software (V3.0.20.19, rhd instruments). The Hsu and Mansfeld formula was used to calculate double-layer capacities from constant phase element values (shown in Equation (S1)) [25,26].

2.3. 46-Point Probe Measurement

The HIOKI RM2610 was used for the determination of the electronic resistances of dry electrode coatings applied on the CC. As the device uses a 46-point probe measurement head, it is herein denoted as the 46-point probe. To obtain a full dataset per sample, three electrode coins were stamped out at different positions of the prepared electrode sheet (approx. 12 × 20 cm²), and a double determination (two measurements per electrode coin) was performed. The results of these six measurements (in total) were used to calculate average values and standard deviations.

To facilitate a better understanding of the HIOKI RM2610 measurement principle, pictures of the measurement pins and measurement head are shown in Figure S1. Additionally, a schematic of the measurement principle is shown in Figure S2. The device determines values for the compound and contact resistance using a combination of resistance measurements and simulation (inverse problem solution). The input parameters needed for the simulation are the thickness of the current collector, thickness of the coating compound and resistivity of the current collector. After starting the measurement, the device performs a contact check to ensure that all measurement pins are in contact with the electrode surface. Afterward, a constant current is applied at the outer pins, and the potential distribution on the electrode surface is measured using the inner pins. Next, the simulation starts by assuming a resistance network in the electrode compound and a resistance layer on the coating CC contact plane. In an iterative procedure, contact and compound resistance values are assumed, and the corresponding surface potential distribution is calculated. The calculated values are then compared with the measured surface potential distribution. In incremental steps, the assumed resistances are changed until the calculated (simulated) surface distribution matches with the measured values. The resistances that enable the calculation of a matching surface distribution are then output as measurement results.

Further information on the measurement principle and application instructions can be found in the technote and instruction manual provided by HIOKI for the device [27].

2.4. 2-Point Measurement

For the 2-point measurement, the prepared electrode sheets’ (approx. 6 × 7 cm²) resistance was measured through a plane with a contact area of 17 cm². Contact was established in a vice under a controlled force of 400 N. To compensate for the slight surfaces roughness between the electrodes and contact plates, a graphite fleece with a thickness of 1 mm was used in between on both sides. The resistance of the electrode sheet was measured until the very point of contact through a 4-point measurement. Because contact resistance and electrode resistance cannot be separated practically, this tends to be a 2-point-measurement. A scheme of the measurement setup is shown in Figure S3 in the Supplementary Information. The resistance was measured with a HP 4338A Milliohmmeter using an AC current of 1 kHz.

3. Results

3.1. The Contact Resistance in EIS on the Example of LMFP

At first, we wanted to identify and characterize the contact resistance contribution in EIS, using LMFP as an illustrative example. Accurately identifying the contact resistance in EIS is crucial for enabling meaningful comparisons with alternative measurement techniques explored later in this study. Additionally, the EIS investigation provides valuable insights into the behavior of contact resistance at varying SoCs and temperatures, settings that are challenging to modify and control in the other measurement techniques. To emphasize the characteristics of electronic resistance, we also analyzed the typical ionic charge-transfer resistance (R_ct) as a comparison.

We conducted EIS studies on three-electrode PAT cells with LMFP cathodes coated on different current collectors with varying press densities to identify the contact resistance’s contribution. This helped us to quantify the impact of the respective measures. The EIS data were fitted to an equivalent circuit model (ECM), shown in Figure 1a. The ECM takes into account the porous structure of the investigated electrode through the use of a transmission line model [24,28,29]. A detailed description of the ECM and its respective parts is provided in Section S4 of the Supplementary Information.

Figure 1b shows Nyquist plots of EIS measurements at 25 °C of the respective LMFP cathodes at 0% SoCs directly after formation. The measured resistance was normalized to the apparent electrode area for better comparability (2.545 cm² for Ø = 18 mm electrodes). In the following discussion, all resistances that were normalized to the apparent electrode area will be designated as areal specific resistance (ASR) with its physical origin as a subscript, as commonly agreed with in the literature. The high-frequency semi-circles, presumed to indicate R_Contact, show apex frequencies of 6 to 77 kHz. The electrical double layer capacities (DL-capacities) of the fitted R-CPE-element are in the range of 1 to 4 µF, which yield areal double layer capacities of 0.46 to 1.49 µF∙cm⁻²_Electrode when normalized to the area of the blank current collector of 2.545 cm². This value is in the expected range for interface DL-capacities [19,30]. Herein, we see a strong indication that a high-frequency semi-circle is not caused by a double layer effect having its origin in the surface area of the electrode active compound (CAM + CB), as this area is way higher than the area of a blank CC. In turn, the areal DL-capacities calculated including the electrode active compound would be far too low compared to a typical double layer capacitance. The DL-capacities were calculated from CPE values using the Hsu and Mansfeld formula (Equation (S1)).

The mid-frequency semi-circle with apex frequencies of around 1 Hz is presumed to indicate the charge-transfer resistance (R_ct). This is validated by the fact that it shows low sensitivity to the degree of calendering (cathode press density) and almost no dependence on the change in current collector. However, the mid-frequency semi-circle strongly depends on the SoC as will be shown and discussed later.

When comparing the magnitude of ASR_Contact in Figure 1b, the uncalendered LMFP cathode on the Al-CC with a high porosity of 61% shows an ASR_Contact of ≈18 Ω∙cm². In soft calendering to a 50% porosity, the ASR_Contact already decreased to ≈4.2 Ω∙cm². ASR_Contact is reduced even further to ≈3 Ω∙cm² if the electrode coating is applied on a primed-CC and calendered to the same 50% porosity. The strong sensitivity of R_Contact to calendering and choice of CC is additional proof that this semi-circle has its physical origin on the interface between the CC and electrode coating. In further comparisons of EIS results, the fitting values derived from this semi-circle will be designated as R_Contact values. We will go into more detail about the impact of electrode porosity when discussing the 46-point probe results.

To investigate the dependence of R_Contact and R_ct on the SoC of the cathode, we conducted EIS measurements in 2% SoC steps and evaluated the results with the explained ECM. The measured resistances are shown in Figure 2a, and the corresponding voltage curve of the LMFP cathode during the measurement procedure is shown in Figure 2b. The R_ct exhibits a strong SoC-dependent behavior, which has—to the best of our knowledge—not been reported before in this detail. It is comparably low between a 0% and approx. 25% SoC, which is characteristic for the Fe²⁺/Fe³⁺ voltage plateau at ≈3.5 V vs. Li/Li⁺. As soon as the Fe²⁺/Fe³⁺ redox reaction is completed, a very large R_ct peak is observed at around the 30% SoC, indicating the transition toward the Mn²⁺/Mn³⁺ redox reaction.

The large overpotential in this area is assumed to be caused by a solid solution reaction regime between the Fe²⁺/Fe³⁺ and Mn²⁺/Mn³⁺ redox reactions, which can lead to a sluggish Li⁺ diffusivity within the crystal [31,32]. In parallel, the voltage profile shows a step increase in cell voltage. As the Mn²⁺/Mn³⁺ redox reaction takes over completely, R_ct drops back to a local minimum value around 35% to 40% SoC, which is in agreement with the beginning of the Mn²⁺/Mn³⁺ voltage plateau. Afterward, R_ct starts to steadily increase for SoC > 40%, a behavior that can be attributed to Li⁺ transport hindrance due to lattice distortion caused by the Jahn–Teller active Mn³⁺ [31]. In contrast to R_ct, the R_Contact shows just minor dependence on the SoC point, which was expectable. These differences in the SoC dependencies of R_ct and R_Contact are a further validation of our allocations of resistance contributions in LMFP. We also observed a characteristic behavior that has not been described before: the R_Contact of the Fe²⁺/Fe³⁺ redox region is slightly higher compared to the R_Contact of the Mn²⁺/Mn³⁺ redox region. A possible explanation for this behavior might be a change in the electronic resistance of the LMFP. Explanations are discussed in more detail in Section S5 in the Supplementary Information. Furthermore, the pulses shown in Figure 2b were used to calculate resistances; the results are compared with EIS results and shown in Supplementary Information Section S6.

When comparing the magnitudes of the different resistances, it can be seen that at 25 °C, at SoCs below 25%, the R_Contact is a dominant resistance contributor. This is further motivation for understanding and optimizing R_Contact in order to minimize overpotentials and enable faster charging.

We want to note that resistance effects that dominate the cell performance at high-current rates such as electrolyte salt gradients were not included in our consideration as they are not measurable with EIS and are, in general, difficult to characterize correctly.

The impact of temperature on resistance contributions was characterized by temperature-dependent EIS measurements. Figure 3a shows the EIS spectra of a calendered LMFP cathode (porosity: 50%) on an Al-CC at a 50% SoC at application-relevant temperatures of 5 °C, 25 °C and 45 °C. For a better comparison, the respective R_Serial value (Table S1) was subtracted from the Z(Re) of each spectrum. It can be seen that the R_Contact (high-frequency semi-circle) is just slightly impacted by temperature, whereas R_ct has a strong temperature dependence.

In the 5 °C measurement, an additional semi-circle occurs with an apex frequency of ≈20 Hz, which is indicated in Figure S6 in the Supporting Information. We could not unambiguously determine the physical origin of this effect. Considering its temperature dependence and frequency range, we presume it to be an effect of electrolyte diffusion in the fine pores of the electrode. The pore shape and pore size distributions can have significant influence on the EIS spectra in this frequency region [33].

For an in-depth analysis, the temperature-dependent EIS data were fitted and afterward plotted according to Arrhenius law, as shown in Figure 3b. The activation energy of the different processes was calculated from the slope of the linearized fit of data points. R_Contact and R_ct exhibited activation energies of −0.8 kJ∙mol⁻¹ (−0.01 eV) and 57.9 kJ∙mol⁻¹ (0.60 eV), respectively. The found negative activation energy value for R_Contact is slightly deviating from the values reported in the literature for other CAMs, which are typically 1–4 kJ∙mol⁻¹ [20,30,34]. However, both values are close to zero and are therefore indicating a low dependence of R_Contact on temperature. As R_Contact involves electron transfer from the Al-CC to the cathode coating, it should also be noted that the electronic resistance of the Al is increasing with increasing temperature (temperature coefficient of ~0.004 K⁻¹) [35] (p. 602). The part of Al conduction in the R_Contact may therefore be a reason for the negative activation energy.

The literature values for R_ct for other CAMS are 0.45 eV (43.4 kJ∙mol⁻¹) for LFP [34], ≈53 kJ∙mol⁻¹ for LCO [20] and 57.6 kJ mol⁻¹ for NCA [4]. These values as well as the found 57.9 kJ∙mol⁻¹ are in a similar area and are indicating a strong temperature dependence of these effects. When optimizing a cell system, it is of crucial importance to understand that electronic resistances such as R_Contact become more and more important with increasing cell temperature as other contributions to total resistance shrink. As can be seen in Figure 3b, R_Contact becomes the largest resistance contribution at a 50% SoC at 45 °C. This impact is even more pronounced for SoCs in the Fe²⁺/Fe³⁺ plateau region. For example, at 10% SoC, R_Contact already becomes the largest resistance contribution at around 15 °C (Figure S7). We take this as a key learning: although adaptions with respect to electronic conductivity may not yield significant power improvements at room temperature, the electronic conductivity can become a dominating factor for the fast charge properties at elevated temperatures. Thus, it is worth it to investigate and understand the individual contributions to the electronic resistance, i.e., R_Contact and R_Compound, in a very detailed manner.

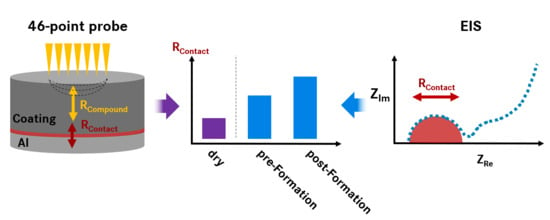
3.2. Comparison of Measurement Methods for Contact Resistance

After the distinct identification and quantification of R_Contact in EIS measurements, we can now compare the results to those of other types of electronic resistance measurement techniques. EIS has the advantage of being an in situ method but has the disadvantage that for each measurement, an electrochemical test cell must be built. This not only limits the sample throughput, but also requires considerable investment in high-quality impedance channels. Additionally, it is difficult to extract the electronic resistance of the electrode compound (R_Compound) from the acquired EIS data.

The electronic resistance contributions within an electrode (R_Compound and R_Contact) can also be tested in setups using the dry electrode coating applied on a CC. In this work, we investigated and compared the well-established 2-point probe method and the 46-point probe method recently commercialized by the company HIOKI. Hereby, our focus is their capability to measure electronic resistance data similar to EIS, using identical electrode samples. As no electrochemical test cell must be built, both methods have the advantages of being fast (≈1 min), easy to handle and implement and free of measurement artefacts originating from cell assembly or other components (e.g., quality variations in reference electrode, electrolyte system, etc.).

The 46-point probe device has the valuable ability to separate the electronic resistivity of the sample into its individual contributions: R_Compound and R_Contact. This is possible due to a sophisticated measuring system checking the potential variations between the probes and solving the inverse problem through simulation within a computation unit. The input parameters for the simulation were the thickness of the electrode compound, thickness of the current collector and specific resistivity of the current collector material. All three parameters are easily accessible and/or can be measured with standard laboratory equipment at high precision.

With the much simpler two-point probe method, it is not possible to separate R_Compound and R_Contact. In typical two-point probe measurements, the electrode is contacted with two metallic conductors of known area perpendicular to the coating surface. Subsequently, the resistance can be measured and normalized to the contact (measurement) area on both sides of the sample. The resulting value includes the combination of R_Compound and R_Contact together with an additional resistance for the contact between metallic conductors and the electrode surface, which must be considered as a measurement artefact.

Figure 4 shows a comparison of R_Contact values determined using different measurement methods (2-point probe, 46-point probe, EIS study) for calendered LMFP cathodes (porosity: 50%) coated on a CC. Different stages of cell preparation were taken into consideration when analyzing data obtained using the 2-point probe (dry electrode), 46-point probe (dry electrode and DMC-wetted electrode) and EIS measurements (electrolyte-wetted electrode in cell). Please note that for the two-point probe, the results include R_Contact and R_Compound, as they are not separable with this method (but as shown below, R_Compound is assumed to be comparably low in these samples). The methods are compared for the LMFP electrode coating (porosity: 50%) on an Al-CC as well as for the LMFP electrode coating (porosity: 50%) on a primed-CC. In this way, we can not only compare the absolute values of each measurement, but also analyze if the relationship between data points for the two electrode types differs based on the method applied.

Firstly, we compare the absolute values of the different methods. The 2-point probe method yields resistance values of 2.30 Ω·cm² (Al-CC) and 0.31 Ω·cm² (primed-CC), which are around 2–4 times higher than those obtained from the 46-point probe measurements of 0.56 Ω·cm² (Al-CC) and 0.14 Ω·cm² (primed-CC). The higher values for the two-point method are presumably caused by additional contact resistances between the metal contact and electrode, which is a major reason why results from two-point methods are dependent on the pressure applied on the metal contact during measurement.

The electrode wetted with electrolyte can have a strong impact on the electric conductivity of electrodes as was shown by other authors [21,36]. Hence, we immersed the LMFP electrodes in dimethyl carbonate (DMC) as a representative electrolyte co-solvent for 20 min and measured the wetted electrodes with the 46-point probe system. We found that the measured R_Contact increased by +40% to 0.79 Ω·cm² (Al-CC) and by +100% to 0.28 Ω·cm² (primed-CC) after wetting with DMC. It is interesting to see that the relative impact of wetting is more pronounced for the LMFP coated on the primed-CC, whereas the absolute increase of +0.14 Ω·cm² is indeed smaller compared to the blank Al-CC with +0.23 Ω·cm². In our opinion, this highlights the superior properties of a carbon primer-modified current collector. Similar behaviors with even higher resistance increases (e.g., 250%) have been reported in the literature, although comparability is limited since the measurements were performed with another resistance probe [36]. These findings give rise to the assumption that electron transport becomes restricted by structural changes and/or electrochemical or other processes that occur during the wetting of electrodes.

In the next step, electrodes were built into three-electrode PAT cells, wetted with electrolyte and measured directly with EIS (before formation). The determined R_Contact values of 3.85 Ω·cm² (Al-CC) and 2.45 Ω·cm² (primed-CC) are 7 times higher than the 46-point probe results for the identical cathode on an Al-CC and 17 times higher for the identical cathode on a primed-CC. These increases may be caused by more complex wetting effects driven by the compounds in the real electrolyte system interacting with the electrode components, such as the swelling of binder or surface reactions with CAM, CB or CC. All of these side effects will slow down the electron conduction or lead to passivation effects between the active electrode layer and the CC. As an artefact from sample preparation, additional resistance may be caused by defects from the punching of electrodes, which could impair the contact strength between the electrode compound and CC. In general, it has to be considered that the 46-point probe system measures on a very small area of 1 mm², whereas in both the EIS and 2-point probe methods, the measurements require a sample area in the scale of several cm². Accordingly, the 46-point probe system enables a more precise spatial resolution over the electrode, which can be used to, for example, check the homogeneity of electronic resistance.

The determination of R_Contact was also conducted after the formation and at the end of life (EOL) of the cells. For these cells, EOL was defined to be after the end of the measurement procedure, which involved EIS measurements at six different temperatures and 50 full cycles at 1 C/1 C.

While the formation procedure itself had a marginal impact on the measured R_Contact value, we observed a severe increase until the EOL according to the EIS data. This increase was about +100% for the electrode coated on an Al-CC sample to 8.27 Ω·cm² and +160% for the electrode coated on a primed-CC to 7.87 Ω·cm². Interestingly, we observed a narrowing of the R_Contact data for the blank vs. carbon primer-coated Al-CC throughout the measurement with strongest impact coming from cyclic ageing. Taking into consideration that the increase in R_Contact over cell lifetime is likely caused by delamination from the current collector and/or cracking inside the electrode active material layer, both of which are induced by the shrinking and swelling of the CAM during delithiation and lithiation, it must be concluded that the binding effect of the carbon primer coating cannot withstand such degradation processes. An increase in R_Contact over cycling has also been reported by other authors [37] and should therefore be considered a highly relevant ageing factor.

After the EOL, a post-mortem analysis (PMA) of the PAT-cells was performed. Delamination at the edges of the electrodes was observed. The electrodes coated on a CC were thoroughly washed in DMC and, after drying, measured with the 46-point probe system. Surprisingly, the electrodes on an Al-CC yielded a R_Contact of 0.15 Ω·cm², which is lower than before the cell build, even though with a large measurement error. The root cause for this behavior could not be clearly identified. However, it could be explained by the re-deposition of dissolved metal ions or the insufficient cleaning of the electrode before the 46-point probe measurement. For the electrode coating on a primed-CC extracted from the PMA, the 46-point probe method shows an increase in R_Contact of around +160% compared to the fresh, dry electrode, to a value of 0.37 Ω·cm². This result is very similar to the data determined from EIS studies and therefore seems reasonable.

Another important message that can be derived from Figure 4 is the ratio of R_Contact between the LMFP cathode on a Al-CC and a primed-CC. For the 2-point probe measurement, the factor is around 7 (meaning that the R_Contact on Al-CC is seven times higher than on a primed-CC), whereas for the 46-point probe on the dry electrode coating, the factor was determined to be 4. The EIS conducted before the formation even shows a factor as small as 1.5. The ratios differ considerably, which makes it difficult to rationally connect the data obtained from the 46-point method with the performance indicated via EIS. However, we have to consider that the observed variations between the factors may be caused by the specific properties of the primed-CC in dry and wet form. As the primer itself is a blend of highly conductive carbon and binder coated on the CC, it may be more prone to the resistance’s increasing effect of electrolyte wetting. Further research is needed to determine if the results from the 46-point probe method can be transferred directly into electrochemical behavior and the EIS of electrodes in active battery cells. This can be relevant, for example, in studies focused on conductive additive variations.

3.3. R_Contact and R_Compound of Different CAMs

As explained above and schematically shown in Figure 5, the 46-point probe method determines separate resistance values for the R_Compound and the R_Contact. R_Compound is given in the units of volume resistivity (Ω·cm, also referred to as material-specific electronic resistance), whereas R_Contact is given as ASR (Ω·cm²). To be able to compare the two contributions, assumptions for the electron flow have to be made. In this work, we assumed that the electron flow occurs in the out-of-plane direction (perpendicular to the CC) and through the full coating thickness. Therefore, the volume resistivity value of the compound can be multiplied by the coating thickness to yield an ASR, making it comparable to R_Contact.

Figure 6a shows the results of the 46-point probe measurement for different combinations of cathode active materials (LMPF, Ni88-NCM-SC, Ni90-NCM-PC) and current collectors. The values for R_Compound are plotted in the unit of resistivity (Ω·cm). The compound resistivity R_Compound of the LMFP cathode coating on an Al-CC increased after DMC wetting from 3.1 Ω·cm to 4.6 Ω·cm. As the compound itself is the same for the LMFP cathode on an Al-CC and primed-CC (porosity of coating for both: 50%), it seems rational to assume that the compound resistance is identical. However, the measurement yields a somewhat lower resistivity for the coating on a primed-CC, with R_Compound being 2.4 Ω·cm. The results measured for Ni88-NCM-SC (2.0 Ω·cm) and Ni90-NCM-PC (1.0 Ω·cm) are provided as reference and for comparison.

As R_Contact is usually given as ASR, it can be difficult to compare it directly to compound resistivities, which are commonly given in Ω·cm. Therefore, the compound resistivity values were multiplied with their respective electrode thicknesses (yielding ASR_Compound) and plotted in combination with R_Contact in Figure 6b. From the 46-point probe measurement, it becomes clearly visible that the ASR_Compound is just a small contributor to the total electronic resistance of the LMFP cathode compared to R_Contact. For the LMFP electrode coating on an Al-CC, the ASR_Compound accounts for only 6% of the overall electronic resistance. For the LMFP electrode on a primed-CC, the ASR_Compound share increases to 16%, as we observe a considerable reduction in R_Contact from 559 mΩ·cm² (Al-CC) to 117 mΩ·cm² (primed-CC) accompanied by a small, unexpected decrease in ASR_Compound from 38 mΩ·cm² to 23 mΩ·cm². In contrast, for Ni90-NCM-PC coated on a blank Al-CC, the ASR_Compound accounts for 36% of the total electronic resistance, which is a significant part. However, the total resistance itself is at a very low level of 11 mΩ·cm² (R_Contact: 7 mΩ·cm² and ASR_Compound: 4 mΩ·cm²).

Please note that the porosities of the NCM cathodes versus LMFP cathodes can vary and that compaction shows a significantly different impact. The root cause can therefore be found in the morphology of the CAM particles. The primary crystallites of the NCMs are sintered at a high temperature to form very dense, spherical or potato-shaped particles with minimal intra-particle pores to avoid electrolyte contact (causing degradation). In clear contrast, the primary carbon-coated LMFP crystallites are agglomerated to spherical particles in a loose manner, leading to a high intra-particle porosity for improved electrolyte infiltration (mandatory for close LMPF–electrolyte contact and the shortest possible Li⁺ diffusion pathways inside the LMFP crystallites). Therefore, even after calendering with the same line force (kN∙mm⁻¹) applied to the cathode surface, the LMFP electrodes still show significantly higher porosities compared to the NCM electrodes as intra-particle porosity remains. We still think a comparison of electronic resistance results is scientifically valid and reasonable as the line force applied for the compaction of all investigated electrodes was approximately the same. A more detailed discussion into the impact of porosities on the electronic resistance is provided in the next section.

It is noteworthy that the total electronic resistance of LMFP (porosity: 50%) on an Al-CC is about two orders of magnitude higher than that of Ni90-NCM-PC (porosity: 27%) on an Al-CC. The total electronic resistance of Ni88-NCM-SC (porosity: 27%) is approx. five times higher than that of Ni90-NCM-PC (porosity: 27%), both coated on a blank Al-CC.

The reason for these differences in electronic resistance are presumably two main factors:

• The electronic conductivity of the cathode active material;
• The morphology of the cathode active material particles.

It is rational to assume that materials with higher electronic conductivity in turn exhibit lower contact resistances. The importance of particle morphology can be derived from a CAM with identical crystal structure. As such, layered oxide Ni88-NCM-SC and Ni90-NCM-PC behave very similar in terms of cell chemistry. Still, the resistance measured for Ni88-NCM-SC is about five times higher, mainly caused by a significantly higher contribution of R_Contact, which is a side effect of the limited anchoring of small SC particles compared to big PC particles. This effect will be explained later.

In general, the resistance values determined using the 46-point probe method were surprisingly small. Through the simple use of Ohm’s law in combination with the measured resistance values, the corresponding overpotentials in electrochemical active battery cells can be predicted. The electrodes have a loading of 3 mAh∙cm⁻². In assuming a high current of 10 C, the resulting overpotentials would be 0.2 mV, 1.2 mV and 18 mV for Ni90-NCM-PC, Ni88-NCM-SC, and LMFP, respectively, with all electrode coatings applied on a blank Al-CC. These overpotentials are negligibly small. However, as discussed in detail before, the electronic resistance becomes significantly larger than the value measured with the 46-point method the moment the dry electrode gets into contact with the electrolyte under the current load conditions inside the electrochemical cell. A significant increase over cell lifetime, which was not automatically captured using the 46-point method, was observed too.

The very low R_Contact of Ni90-NCM-PC was also verified using the EIS spectra in Figure 7. The spectra show no evidence of any R_Contact. Even if the magnitude of R_Contact would be 10 times larger in EIS than in the 46-point method (a value similar to that of Ni88-NCM-SC), its impact would still be negligible, as indicated by the thickness of the red line for a 70 mΩ∙cm² resistance contribution. These findings indicate that for Ni90-NCM-PC, a further decrease in conductive additive can be applied in the recipe without any loss in performance. In this case, the forecast based on 46-point probe data, namely that R_Contact will be insignificant in the case of Ni90-NCM-PC, proved to be correct. These findings highlight the great potential of the 46-point probe method when applied as a fast and easy predictor of electronic resistance for various electrodes and cell designs. It opens the opportunity for, e.g., fast iterations in electrode recipe optimization based on different active materials, conductive additives and current collector combinations without the need for testing in electrochemical cells. This aspect is currently under further investigation in our group and will be reported on in the near future.

3.4. Influence of Porosity on Electronic Resistances for Different CAMs

As addressed above and also shown in various published EIS studies, R_Contact usually exhibits a strong dependence on electrode porosity. Figure 8a discloses the dependences of ASR_Contact and ASR_Compound derived from the 46-point probe measurement on electrode porosity for Ni90-NCM-PC, Ni88-NCM-SC and partly for LMFP. It should be noted that for Ni90-NCM-PC and Ni88-NCM-SC, a cathode coating with 50% porosity corresponds to the uncalendered state, whereas for LMFP, a 50% porosity can be reached only through significant calendering (≈62% porosity in uncalendered state). The following strong impacts of calendering are clearly visible for the NCM cathodes:

• In the first calendering step from 50% to 35% porosity, the total electronic resistance decreases by a factor of about 10, in the case of the Ni90-NCM-PC, from 367 mΩ·cm² to 21 mΩ·cm² and for Ni88-NCM-SC, from 1330 mΩ·cm² to 190 mΩ·cm².
• In the second step to 27% porosity, the resistance is again roughly halved to 11 mΩ·cm² for Ni90-NCM-PC and to 48 mΩ·cm² for Ni88-NCM-SC.
• Starting from the next calendering steps to porosity ≤ 21%, a saturation point seems to be reached for both samples, and there is only a marginal further decrease in resistance.

Interestingly, in contrast to the behaviors of the NCM samples, the LMFP cathode shows no decrease in total electronic resistance when calendered from 50% to 35% porosity. However, the ratio between ASR_Contact and ASR_Compound changes slightly.

In Figure S8, the electronic resistances for Ni90-NCM-PC at two different loadings are shown. The electrode with high loading (4 mAh∙cm⁻²) shows a similar dependence on electrode porosity as observed for the 3 mAh∙cm⁻². When examining R_Compound, we can assume that the compound resistivity (Ω∙cm) is equal for identical cathode recipes at different loadings. Considering the fact that at the same porosity, the thickness of the high-loading cathode (4 mAh∙cm⁻²) is +33% higher than the low-loading cathode (3 mAh∙cm⁻²), it is rational to conclude that the ASR_Compound increases by +33% as well. For the Ni90-NCM-PC cathodes in Figure 8a, for example, at 21% porosity, the ASR_Compound is 3.4 mΩ·cm² (low loading) and 4.6 mΩ·cm² (high loading). The difference is +35%, which is very close to the predicted value. At other electrode porosities, the difference is in a similar range. The confirmation of these assumptions strongly indicates that the measured compound resistivity is a reliable value when normalized to electrode thickness (i.e., volume resistivity in Ω∙cm).

Figure 8b shows SEM pictures and a schematic representation of the electrodes. We observed that the hard Ni90-NCM-PC particles were strongly dented into the Al-CC during calendering, thereby making full-body contact with the CC. We call this effect “anchoring”. For the LMFP coating, in contrast, this anchoring does not happen. We presume that the secondary LMFP structure consisting of agglomerated, nanosized primary particles plus pores (for better electrolyte access) is partially crushed during alendaring. Due to this effect, the calendering force is homogeneously distributed within the active material layer itself, forming a very compact, dense layer of numerous small primary particles but no indentation of particles into the CC. The observed absence of particle anchoring results in insufficient electronic contact (measurably high R_Contact). The absence of particle anchoring also has an impact on the adhesion strengths of the coatings. The results of 90° peel strength tests are presented in Figure S9. With higher degrees of particle anchoring, the peel strength is increasing. Therefore, it is possible, under certain limitations (same formulation, similar CAM), to use the peel strength as a rough proxy for the electronic resistance of a cathode [38]. Even though there were significant differences in peel strength, all coatings had sufficient adhesion on the CC. These results emphasize the significant influence of porosity on the electronic resistance of electrodes and underline that porosity and particle morphology have to be carefully considered when evaluating or comparing published data.

4. Conclusions

LMFP and NCM811 cathodes were prepared with CAM ratios, electrode loadings and press densities relevant for application in automotive battery cells. Through EIS studies, the temperature dependence, SoC dependence and impact of current collector (Al-CC vs. primed-CC) on the R_Contact in LMFP cathode coatings were determined. The results obtained for R_Contact via EIS were compared to those of a 2-point probe and 46-point probe on the example of LMFP cathodes for different stages of cell preparation and over the cell lifetime. The ratio and magnitude of the two electronic resistance contributions (R_Contact and R_Compound) derived from the 46-point probe method were examined in detail not only for LMFP, but also for state-of-the-art Ni-rich NCM electrodes. Density and morphology were identified and discussed as main impact parameters for the electronic resistance of cathodes. From our study, we can draw the following main conclusions:

• The R_Contact in LMFP cathodes shows a minor dependence on the SoC and temperature (activation energy = −0.8 kJ∙mol⁻¹), but significant dependence on calendering and the current collector.
• The R_Contact in LMFP cathodes becomes a performance-determining factor at low SoCs and high temperatures, as under these conditions, the other resistance contributions are reduced significantly.
• The comparison of measurement techniques reveals significant variations between the results obtained. The total electronic resistance values determined are in the following order: EIS > 2-point probe method > 46-point probe method.
• The total electronic resistances of different electrodes can vary over several orders of magnitude depending on chemical composition and crystal structure (band gap), doping elements, carbon coating, etc.

The 46-point method revealed that R_Contact is the main contributor to electronic resistance for LMFP and low-density NCM cathodes for the electrode recipes used in this publication. At higher press densities (after strong calendering), the R_Contact is reduced considerably, and the impact of R_Compound becomes more dominant.

As EIS is an “in situ” method and is therefore closest to the actual application of the electrochemical system (active battery electrode), it can be assumed that these results are the most relevant for later use. Even though the 46-point probe measurement did not reproduce the resistances extracted from the EIS studies with complete accuracy, it remains a valuable tool for quickly estimating electronic resistances and optimizing electrode compositions accordingly. This work presents key contributions to the coherent and broad field of the characterization of electronic resistances. It enables a better understanding of how parameters influence electrochemical performances. Furthermore, it helps to assess the comparability of electronic resistance results reported elsewhere.

The next relevant step is the correlation of electrochemical performance data with electronic resistance tests, while taking into consideration the influence of recipe parameters. Our research team is currently devoted to this topic, and results will be published in the near future.