1. Introduction
After years of development in the electric vehicle (EV) industry, lithium-ion batteries (LiBs) have become the main source of EVs [
1,
2]. Although EVs’ market share has steadily increased in recent years, their safety and lifespan have always been essential issues restricting their long-term use. Therefore, the battery management system (BMS) is implemented to monitor the health state of the battery system and to ensure safety and reliable operation. State of health (SOH) is an important indicator to evaluate the health state of the battery, and it can be expressed as follows:
where
and
are the actual and rated capacity, respectively.
SOH estimation is a key function of the BMS [
3]. In the past decades, the existing SOH estimation approaches can be classified as direct measurement methods and indirect analytical methods [
4]. Typical direct measurement methods include capacity measurement based on the coulomb counting method, internal resistance measurement based on specific tests, and the impedance measurement method, which relies on electrochemical impedance spectroscopy (EIS). The direct measurement methods suit laboratory conditions but not onboard applications. Indirect analytical methods can be further classified as model-based and data-driven methods. A high-fidelity battery model, such as the electrochemical model [
5], equivalent circuit model (ECM) [
6], empirical model, and stochastic degradation model, is first built for the model-based methods. Then, the well-parameterized battery model is integrated with filter algorithms to estimate the SOH [
7,
8].
Owing to advanced techniques, such as 5G, cloud computing, and the Internet of Things (IoT), the data-driven approaches have found successful applications across different domains of LiBs, such as the production of LiBs [
9,
10], material design [
11], fast charging strategy [
12], safety control [
13], as well the state estimation, especially the SOH estimation. Compared with the model-based method, the superiority of the data-driven method is that it considers the battery as a black box, and the pre-determined battery model is not required anymore. Machine learning (ML) methods can mine the hidden degradation information from the aging data [
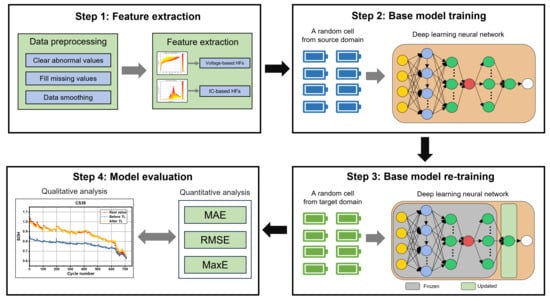
14]. The typical flowchart to develop an ML-based SOH estimation method is shown in
Figure 1. Data processing and model training are two critical steps that determine the performance of the SOH estimation [
15]. For data preprocessing, the so-called health features (HFs) [
16] are extracted from the raw data, which is the foundation and key for ML methods. The extraction methods include direct extraction and indirect extraction methods [
17]. The direct extraction method obtains HFs based on the measured raw data directly. For example, the charging time of constant current (CC) and constant voltage (CV) processes [
18,
19], the slope of the curve during the end of the CC charging process [
20], and voltage discrepancy at uniform time intervals [
21] were used as HFs in recently published papers. The indirect extraction method obtains HFs based on the reconstructed curves. Commonly used reconstructing methods are incremental capacity (IC) analysis [
22], differential voltage (DV) analysis [
23], and differential temperature (DT) analysis [
16]. For example, multiple peaks can be seen in the IC curve, and each peak reflects the phase transition when the battery is working. With the aging of LiBs, the IC curve shows a specific trend of change, especially the peaks. Therefore, the value, position, width, slope, and area under each peak are often used as HFs. For these kinds of reconstructed curves, filtering methods are required to eliminate the influence of noise. Other indirect HFs include open circuit voltage and ohmic resistance within the ECM or polarization capacitance and resistance derived from electrochemical impedance [
24,
25]. The main drawback is that additional algorithms are required, increasing its difficulty. Other variables, namely, the sample entropy [
26,
27] and Kullback–Leibler distance [
28], are also used as HFs for SOH estimation.
Based on the pre-processed HFs and SOH values, different ML approaches are employed to train the SOH estimation model, including shallow neural networks, deep learning methods, Gaussian process regression (GPR), support vector machine (SVM), and ensemble learning methods. Although developing the data-driven-based SOH estimation method requires numerous aging data, more and more public aging datasets are available online thanks to the joint efforts of all researchers, which is beneficial for developing advanced health prognostic methods. Some popular public aging datasets are given in
Table 1.
Currently, the HF-based ML methods for SOH estimation are usually developed based on a single battery dataset, which means that the effectiveness and applicability of the HF extraction strategy cannot be guaranteed toward other battery datasets. For example, Fan et al. [
37] used different combinations of HFs to train the SOH estimation model toward the NASA and Oxford aging datasets, respectively. When choosing appropriate HFs, in addition to the principles of easy acquisition, suitability for practical conditions, and a highly relevant degree, the adaptability and universality of different types of batteries are significant. Therefore, it is essential to explore a robust HF extraction strategy that is especially applicable to diverse material types and varied working conditions [
38].
On the other hand, when using a single battery dataset to train the SOH estimation model, it usually assumes that the training and testing data have the same distribution. However, such an assumption does not work for different types of batteries or working conditions. Therefore, the well-trained SOH estimation model cannot guarantee an acceptable estimation performance toward other battery datasets. In this case, transfer learning (TL) technology is utilized for such problems [
39]. Two strategies, namely, the model parameter fine-tuning and domain adaption methods, are used in recent works for SOH estimation [
40].
For the fine-tuning strategy, the data from the source domain is used to train the base model first, and then the specific layer in the base model is re-trained using the data from the target domain while other layers keep frozen. Huang et al. [
41] proposed a deep learning model, and the principles of either fine-tuning or rebuilding were applied based on whether the target domain shared the same type of LiBs. However, the HFs used in the source domain and target domain were different according to different source and target domain selections. In another work [
42], according to whether the feature expression score (FES) was greater than a threshold, the last fully connected (FC) layer of the base model was fine-tuned or reconstructed. However, the proposed method was only validated inside the same aging datasets (e.g., the NASA aging dataset). In addition, the need for individual fine-tuning for each battery in the target domain significantly increases computational expenses. Zhu et al. [
35] randomly selected a battery from the target domain and used its complete cyclic data for TL. They also compared different data selection strategies and concluded that using data from a randomly selected battery can achieve much better results than that from the time-series-based data. In addition, the fine-tuning strategy was applied for the SOH estimation of the battery pack [
43].
Domain adaptation methods aim to reduce the disparity in feature distributions between the source and target domains, ultimately enhancing the generalization and accuracy of data-driven models. [
44]. Li et al. [
45] used transfer component analysis (TCA) to minimize data differences and eliminate redundancy across various datasets. In another work [
46], joint distribution adaptation (JDA) was employed to achieve simultaneous adaptation of both the marginal probability and the conditional probability distribution. Fu et al. [
38] proposed a feature mapping strategy that first identified the reference cell (RC) and optimal matching cell (OMC) in the source domain and target domain, respectively. Then, a linear matching approach was developed. The cyclic data of the OMC in the target domain was used to re-train the base model. However, for different source and target domains, it is necessary to identify the RC and OMC first, increasing the complexity of the algorithm.
Based on the analysis above, some challenges need to be considered: (1) a universal and effective HF extraction strategy is imperative, especially for different types of batteries and different working conditions; (2) how accurate and robust SOH estimation toward different types of batteries using TL can be ensured. To address these challenges, a universal HF extraction strategy and a deep learning neural network-based transfer learning method are established for SOH estimation in this paper. Three open-source aging datasets, namely the Oxford, CALCE, and NASA aging datasets, are used to validate the effectiveness of the proposed algorithms. The main contributions are as follows:
- (1)
To comprehensively reflect the aging characteristics of LiBs and apply them to different battery types and working conditions, a universal HF extraction strategy is proposed. Only partial voltage and current information is required to extract four straightforward and highly relevant HFs.
- (2)
To learn the long-term dependency between the HFs and capacity and fulfill TL, a deep learning neural network consisting of the long short-term memory (LSTM) and FC layers is proposed in this paper. For the same battery type (or in the same aging dataset), the proposed neural network is trained using a random-selected battery, and other batteries are used to test the model directly without using the TL strategy.
- (3)
To achieve accurate and robust SOH estimation of different types of batteries and different working conditions, the fine-tuning-based TL strategy is used in this paper. The basic principle is to use a random-selected battery in the source domain to train the base model, and then use a random-selected battery in the target domain to re-train the base model, where only the last layer is re-trained and the other layers are frozen.
- (4)
Comprehensive verifications are conducted using three popular open-source aging datasets, namely Oxford, CALCE, and NASA aging datasets. Sixteen batteries, featuring two distinct cathode material types, are subjected to cycling under five different operating conditions to assess the efficacy of the proposed methods.
The remainder of the paper is organized as follows:
Section 2 introduces the experimental datasets and feature extraction strategy.
Section 3 explains the used algorithms.
Section 4 gives the results and discussions. Finally, conclusions are summarized in
Section 5.