Rapid Interactive and Intuitive Segmentation of 3D Medical Images Using Radial Basis Function Interpolation †
Abstract
:1. Introduction
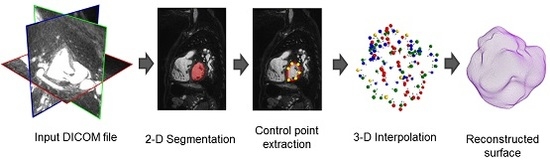
2. Methods
2.1. Smart Brush
2.2. Control Point Extraction
2.3. Control Point Merging
2.3.1. Contour Intersection
2.3.2. Classification and Merging
2.4. 3D Interpolation
2.5. Surface Reconstruction
3. Evaluation and Results
3.1. Smart Brush Evaluation
3.2. 3D Interpolation Evaluation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Disclaimer
Abbreviations
| A-HRBF | Adaptive Hermite Radial Basis Function |
| HRBF | Hermite Radial Basis Function |
| RBF | Radial Basis Function |
| MRI | Magnetic Resonance Imaging |
| ROI | Region of Interest |
| CP | Control Point |
References
- Kurzendorfer, T.; Forman, C.; Schmidt, M.; Tillmanns, C.; Maier, A.; Brost, A. Fully Automatic Segmentation of the Left Ventricular Anatomy in 3D LGE-MRI. J. Comput. Med. Imaging Graph. 2017, 59, 13–27. [Google Scholar] [CrossRef] [PubMed]
- Mirshahzadeh, N.; Kurzendorfer, T.; Fischer, P.; Pohl, T.; Brost, A.; Steidl, S.; Maier, A. Radial Basis Function Interpolation for Rapid Interactive Segmentation of 3D Medical Images. In Proceedings of the Annual Conference on Medical Image Understanding and Analysis, Edinburgh, UK, 11–13 July 2017; Springer: Berlin, Germay, 2017; pp. 651–660. [Google Scholar]
- Mortensen, E.N.; Barrett, W.A. Interactive Segmentation with Intelligent Scissors. Graph. Model. Image Process. 1998, 60, 349–384. [Google Scholar] [CrossRef]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast Approximate Energy Minimization via Graph Cuts. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Grady, L. Random Walks for Image Segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1768–1783. [Google Scholar] [CrossRef] [PubMed]
- Amrehn, M.; Gaube, S.; Unberath, M.; Schebesch, F.; Horz, T.; Strumia, M.; Steidl, S.; Kowarschik, M.; Maier, A. UI-Net: Interactive Artificial Neural Networks for Iterative Image Segmentation Based on a User Model. In EG VCBM 2017; Rieder, C., Ritter, F., Hotz, I., Merhof, D., Eds.; Eurographics Association: Aire-la-Ville, Switzerland, 2017; pp. 143–147. [Google Scholar]
- Malmberg, F.; Strand, R.; Kullberg, J.; Nordenskjöld, R.; Bengtsson, E. Smart paint a new interactive segmentation method applied to MR prostate segmentation. In Proceedings of the MICCAI Grand Challenge: Prostate MR Image Segmentation, Nice, France, 1–5 October 2012. [Google Scholar]
- Parascandolo, P.; Cesario, L.; Vosilla, L.; Pitikakis, M.; Viano, G. Smart brush: A real time segmentation tool for 3D medical images. In Proceedings of the 2013 8th International Symposium on Image and Signal Processing and Analysis (ISPA), Trieste, Italy, 4–6 September 2013; pp. 689–694. [Google Scholar]
- Boykov, Y.; Kolmogorov, V. Computing geodesics and minimal surfaces via graph cuts. In Proceedings of the International Conference on Computer Vision, Nice, France, 13–16 October 2003; Volume 3, pp. 26–33. [Google Scholar]
- Morse, B.S.; Yoo, T.S.; Rheingans, P.; Chen, D.T.; Subramanian, K.R. Interpolating implicit surfaces from scattered surface data using compactly supported radial basis functions. In Proceedings of the ACM SIGGRAPH 2005 Courses, Los Angeles, CA, USA, 31 July–4 August 2005; ACM: New York, NY, USA, 2005; p. 78. [Google Scholar]
- Duchon, J. Splines minimizing rotation-invariant semi-norms in Sobolev spaces. In Constructive Theory of Functions of Several Variables; Springer: Berlin, Germany, 1977; pp. 85–100. [Google Scholar]
- Carr, J.C.; Beatson, R.K.; Cherrie, J.B.; Mitchell, T.J.; Fright, W.R.; McCallum, B.C.; Evans, T.R. Reconstruction and representation of 3D objects with radial basis functions. In Proceedings of the 28th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 12–17 August 2001; ACM: New York, NY, USA, 2001; pp. 67–76. [Google Scholar]
- Turk, G.; O’brien, J.F. Modelling with implicit surfaces that interpolate. ACM Trans. Graph. 2002, 21, 855–873. [Google Scholar] [CrossRef]
- Ijiri, T.; Yoshizawa, S.; Sato, Y.; Ito, M.; Yokota, H. Bilateral Hermite Radial Basis Functions for Contour-based Volume Segmentation. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2013; Volume 32, pp. 123–132. [Google Scholar]
- Tomasi, C.; Manduchi, R. Bilateral filtering for gray and color images. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 7 January 1998; pp. 839–846. [Google Scholar]
- Abbena, E.; Salamon, S.; Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Elkan, C. Nearest Neighbor Classification. Encycl. Database Syst. 2011. [Google Scholar] [CrossRef]
- Macedo, I.; Gois, J.P.; Velho, L. Hermite Radial Basis Functions Implicits. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2011; Volume 30, pp. 27–42. [Google Scholar]
- Brazil, E.V.; Macedo, I.; Sousa, M.C.; de Figueiredo, L.H.; Velho, L. Sketching Variational Hermite-RBF Implicits. In Proceedings of the Seventh Sketch-Based Interfaces and Modeling Symposium, Annecy, France, 7–10 June 2010; Eurographics Association: Aire-la-Ville, Switzerland, 2010; pp. 1–8. [Google Scholar]












© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurzendorfer, T.; Fischer, P.; Mirshahzadeh, N.; Pohl, T.; Brost, A.; Steidl, S.; Maier, A. Rapid Interactive and Intuitive Segmentation of 3D Medical Images Using Radial Basis Function Interpolation. J. Imaging 2017, 3, 56. https://doi.org/10.3390/jimaging3040056
Kurzendorfer T, Fischer P, Mirshahzadeh N, Pohl T, Brost A, Steidl S, Maier A. Rapid Interactive and Intuitive Segmentation of 3D Medical Images Using Radial Basis Function Interpolation. Journal of Imaging. 2017; 3(4):56. https://doi.org/10.3390/jimaging3040056
Chicago/Turabian StyleKurzendorfer, Tanja, Peter Fischer, Negar Mirshahzadeh, Thomas Pohl, Alexander Brost, Stefan Steidl, and Andreas Maier. 2017. "Rapid Interactive and Intuitive Segmentation of 3D Medical Images Using Radial Basis Function Interpolation" Journal of Imaging 3, no. 4: 56. https://doi.org/10.3390/jimaging3040056
APA StyleKurzendorfer, T., Fischer, P., Mirshahzadeh, N., Pohl, T., Brost, A., Steidl, S., & Maier, A. (2017). Rapid Interactive and Intuitive Segmentation of 3D Medical Images Using Radial Basis Function Interpolation. Journal of Imaging, 3(4), 56. https://doi.org/10.3390/jimaging3040056