Photonic Crystal Characterization of the Cuticles of Chrysina chrysargyrea and Chrysina optima Jewel Scarab Beetles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimens and Sample Preparation
2.2. Visual appearance
3. Results and Discussion
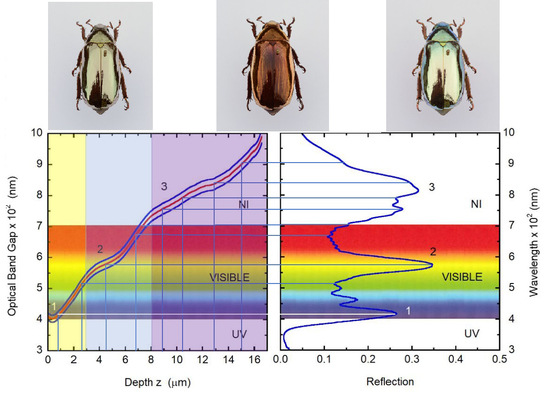
3.1. Measured Reflection Spectra
3.2. Scanning Electron Microscopy Analysis and Morphology of the Cuticle
3.3. Composition
3.4. Modeling Synthetic Reflection Spectra with Berreman’s Formalism
3.5. Photonic Crystal Characterization of Twisted Structures with Graded Pitches
3.6. Optical Characterization of the Cuticle of C. chrysargyrea Scarabs
3.7. Optical Characterization of the Cuticle of C. optima Scarabs
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Michelson, A.A. On metallic colouring in beetles and insects. Philos. Mag. Ser. 6 1991, 21, 554–567. [Google Scholar] [CrossRef]
- Strutt, J.W. On the optical character of some brilliant animal colours. Philos. Mag. 1919, 6, 98–111. [Google Scholar]
- Strutt, R.J. Iridescent colours in nature from the stand-point of physical optics. J. Sci. Instrum. 1930, 7, 34–40. [Google Scholar]
- Newton, I. Optiks: A Treatise of the Reflections, Refractions, Inflections, and Colours of Light; Royal Society: London, UK, 1704. [Google Scholar]
- Hook, R. Micrographia: Or Some Physiological Descriptions of Minute Bodies Made by Magnifying Glasses with Observation and Inquiries Thereupon; Royal Society: London, UK, 1665. [Google Scholar]
- Durrer, H.; Villiger, W. Schillerfarben von Euchroma gigantea (L.): (Coleoptera: Buprestidae): Elektronenmikroscopische Untersuchung der Elytra. Int. J. Insect Embryol. 1972, 1, 233–240. [Google Scholar] [CrossRef]
- Stavenga, D.G.; Wilts, B.D.; Leertouwer, H.L.; Hariyama, T. Polarized iridescence of the multilayered elytra of the Japanese jewel beetle, Chrysochroa fulgidissima. Philos. Trans. R. Soc. B 2011, 366, 709–723. [Google Scholar] [CrossRef] [PubMed]
- Neville, A.C.; Caveney, S. Scarabaeid beetle exocuticle as an optical analogue of cholesteric liquid crystals. Biol. Rev. 1969, 44, 531–562. [Google Scholar] [CrossRef] [PubMed]
- Pye, J.D. The distribution of circularly polarized light reflection in the Scarabaeoidea (Coleoptera). Biological J. Linn. Soc. 2010, 100, 585–596. [Google Scholar] [CrossRef] [Green Version]
- Guarín-Zapata, N.; Gomez, J.; Yaraghi, N.; Kisailus, D.; Zavattieri, P.D. Shear wave filtering in naturally-ocurring Bouligand structures. Acta Biomater. 2015, 23, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Vignolini, S.; Rudall, P.J.; Rowland, A.V.; Reed, A.; Moyroud, E.; Faden, R.B.; Baumberg, J.J.; Glover, B.J.; Steiner, U. Pointillist structural color in Pollia fruit. Proc. Natl. Acad. Sci. USA 2012, 109, 15712–15715. [Google Scholar] [CrossRef] [PubMed]
- Wilts, B.D.; Whitney, H.M.; Glover, B.J.; Steiner, U.; Vignolini, S. Natural helicoidal structures: Morphology, self-assembly and optical properties. Mater. Today Proc. 2014, 1S, 177–185. [Google Scholar] [CrossRef]
- Miao, J.; Wu, Y.Q.; Li, K.B.; Jiang, Y.L.; Gong, Z.J.; Duan, Y.; Li, T. Evidence for visually mediated copulation frequency in the scarab beetle Anomala corpulenta. J. Insect Behav. 2015, 28, 175–182. [Google Scholar] [CrossRef]
- Allahverdyan, K.; Galstian, T.; Gevorgyan, A.; Hakobyan, R. Could the cuticle of beetles serve also for their radiative thermoregulation? Opt. Photonics J. 2013, 3, 17–22. [Google Scholar] [CrossRef]
- Ling, S.; Kaplan, D.L.; Buehler, M.J. Nanofibrils in nature and materials engineering. Nat. Rev. 2018, 3, 18016. [Google Scholar] [CrossRef]
- Allahverdyan, K.; Galstian, T. Electrooptic jumps in natural helicoidal photonic bandgap structures. Opt. Express 2011, 19, 4611–4617. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Urbas, A.M.; Li, Q. Nature-inspired emerging chiral liquid crystal nanostructures: From molecular self-assembly to DNA mesophase and nanocolloids. Adv. Mater. 2018, 30, 1801335. [Google Scholar] [CrossRef] [PubMed]
- Carter, I.E.; Weir, K.; McCall, M.W.; Parker, A.R. Variation of the circularly polarized light reflection of Lomaptera (Scarabaeidae) beetles. J. R. Soc. Interface 2016, 13, 0015. [Google Scholar] [CrossRef] [PubMed]
- Brink, D.J.; van der Berg, N.G.; Prinsloo, L.C.; Hodgkinson, I.J. Unusual coloration in scarabaeid beetles. J. Phys. D Appl. Phys. 2007, 40, 2189–2196. [Google Scholar] [CrossRef] [Green Version]
- Jewell, S.A.; Vukusic, P.; Roberts, N.W. Circularly polarized colour reflection from helicoidal structures in the beetle Plusiotis boucardi. New J. Phys. 2007, 9, 99. [Google Scholar] [CrossRef]
- Fernández del Río, L.; Arwin, H.; Järrendahl, K. Polarizing properties and structure of the cuticle of scarab beetles from the Chrysina genus. Phys. Rev. E 2016, 94, 012409. [Google Scholar] [CrossRef] [PubMed]
- Goldstein, D.H. Polarization properties of Scarabaeidae. Appl. Opt. 2006, 45, 7944–7950. [Google Scholar] [CrossRef] [PubMed]
- Seago, A.E.; Brady, P.; Vigneron, J.P.; Schultz, T.D. Gold bugs and beyond: A review of iridescence and structural colour mechanism in beetles (Coleoptera). J. R. Soc. Interface 2009, 6, S165–S184. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Crne, M.; Park, J.O.; Srinivasarao, M. Structural origin of circularly polarized iridescence in jeweled beetles. Science 2009, 325, 449–451. [Google Scholar] [CrossRef] [PubMed]
- Fernández del Río, L.; Arwin, H.; Järrendahl, K. Polarizing properties and structural characteristics of the cuticle of the scarab beetle Chrysina gloriosa. Thin Solid Films 2014, 571, 410–415. [Google Scholar] [CrossRef]
- Fernández del Río, L.; Arwin, H.; Järrendahl, K. Polarization of light reflected from Chrysina gloriosa under various illuminations. Mater. Today Proc. 2015, 1S, 172–176. [Google Scholar]
- McDonald, L.T.; Starkey, T.A.; Vukusic, P. Photonic architectures in beetles: Twists and iridescence. Int. J. Des. Nat. Ecodyn. 2014, 9, 266–275. [Google Scholar] [CrossRef]
- Finlayson, E.D.; McDonald, L.T.; Vukusic, P. Optically ambidextrous circularly polarized reflection from the chiral cuticle of the scarab beetle Chrysina resplendens. J. R. Soc. Interface 2017, 14, 0129. [Google Scholar] [CrossRef] [PubMed]
- Mouchet, S.R.; Lobet, M.; Kolaric, B.; Kaczmarek, A.M.; Van Deun, R.; Vukusik, P.; Deparis, O.; Van Hooijdonk, E. Controlled fluorescence in a beetle’s photonic structure and its sensitivity to environmentally induced changes. Proc. R. Soc. B 2018, 283, 20162334. [Google Scholar] [CrossRef] [PubMed]
- Campos-Fernández, C.; Azofeifa, D.E.; Hernández-Jiménez, M.; Ruiz-Ruiz, A.; Vargas, W.E. Visible light reflection spectra from cuticle layered materials. Opt. Mater. Express 2011, 1, 85–100. [Google Scholar] [CrossRef]
- Libby, E.; Azofeifa, D.E.; Hernández-Jiménez, M.; Bargoza-Aguilar, C.; Solís, A.; García-Aguilar, I.; Arce-Marenco, L.; Hernández, A.; Vargas, W.E. Light reflection by the cuticle of C. aurigans scarabs: A biological broadband reflector of left handed circularly polarized light. J. Opt. 2014, 16, 082001. [Google Scholar] [CrossRef]
- Hernández-Jiménez, M.; Azofeifa, D.E.; Libby, E.; Barboza-Aguilar, C.; Solís, A.; Arce-Marenco, L.; García-Aguilar, I.; Hernández, A.; Vargas, W.E. Qualitative correlation between structural chirality through the cuticle of Chrysina aurigans scarabs and left-handed circular polarization of the reflected light. Opt. Mater. Express 2014, 4, 2632–2645. [Google Scholar] [CrossRef]
- Azofeifa, D.E.; Hernández-Jiménez, M.; Libby, E.; Solís, A.; Barboza-Aguilar, C.; Vargas, W.E. A quantitative assessment approach of feasible optical mechanisms contributing to structural color of golden-like Chrysina aurigans scarab beetles. J. Quant. Spectrosc. Radiat. Transf. 2015, 160, 63–74. [Google Scholar] [CrossRef]
- Vargas, W.E.; Hernández-Jiménez, M.; Libby, E.; Azofeifa, D.E.; Solís, Á.; Barboza-Aguilar, C. Broadening of effective photonic band gaps in biological chiral structures: From intrinsic narrow band gaps to brand band reflection spectra. Europhys. Lett. 2015, 111, 064001. [Google Scholar] [CrossRef]
- Vargas, W.E.; Hernández-Jiménez, M.; Libby, E.; Azofeifa, D.E.; Barboza, C.; Solís, A. Light reflection by cuticles of Chrysina jewel scarabs: Optical measurements, morphology characterization, and theoretical modeling. Opt. Photonics J. 2016, 6, 146–163. [Google Scholar] [CrossRef]
- Agez, G.; Bayon, C.; Mitov, M. Multiwavelength micromirrors in the cuticle of scarab beetle Chrysina gloriosa. Acta Biomater. 2016, 48, 357–367. [Google Scholar] [CrossRef] [PubMed]
- Carter, I.E. An Experimental Study in the Variation of the Near-Circular Polarisation Properties in Scarabaeoidae Beetles; Imperial College: London, UK, 2017. [Google Scholar]
- Caveney, S. Cuticle reflectivity and optical activity in scarab beetles: The role of uric acid. Proc. R. Soc. Lond. B 1971, 178, 205–225. [Google Scholar] [CrossRef] [PubMed]
- Ninomiya, Y.; Tanaka, K.; Hayakawa, Y. Mechanisms of black and white stripe pattern formation in the cuticles of insect larvae. J. Insect Physiol. 2006, 52, 638–645. [Google Scholar] [CrossRef] [PubMed]
- Goh, K.S.; Sheu, H.S.; Hua, T.E.; Kang, M.H.; Li, C.W. Uric acid spherulites in the reflector layer of firefly light organ. PLoS ONE 2013, 8, e56406. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, S. Structural Colors in the Realm of Nature; World Scientific: Singapore, 2008. [Google Scholar]
- De Gelder, J.; De Gussem, K.; Vandenabeele, P.; Moens, L. Reference database of Raman spectra of biological molecules. J. Raman Spectrosc. 2007, 38, 1133–1147. [Google Scholar] [CrossRef] [Green Version]
- Pucetaite, M.; Velicka, M.; Pilipavicius, J.; Beganskiene, A.; Ceponkus, J.; Sablinskas, V. Uric acid detection by means of SERS spectroscopy on dried Ag colloidal drops. J. Raman Spectrosc. 2016, 47, 681–686. [Google Scholar] [CrossRef]
- Pearson, F.G.; Marchessault, R.H.; Liang, C.Y. Infrared spectra of crystalline polysaccharides. V. Chitin. J. Polym. Sci. 1960, 43, 101–116. [Google Scholar] [CrossRef]
- Kim, J. Noninvasive uric acid monitoring device using near-infrared spectroscopy. J. Biosens. Bioelectron. 2015, 6, 1000188. [Google Scholar] [CrossRef]
- Negrea, P.; Caunii, A.; Sarac, I.; Butnariu, M. The study of infrared spectrum of chitin and chitosan extract as potential sources of biomass. Dig. J. Nanomater. Biostruct. 2015, 10, 1129–1138. [Google Scholar]
- Lautié, A.; Froment, F.; Novak, A. Relationship between NH stretching frequencies and N…O distances of crystals containing NH…O hydrogen bonds. Spectrosc. Lett. 1976, 9, 289–299. [Google Scholar] [CrossRef]
- Zellelow, A.Z.; Abiye, M.; Fink, D.A.; Ford, C.E.; Kim, K.H.; Sours, R.E.; Yannette, C.M.; Swift, J.A. Doping uric acid crystals. 1. Uric acid dihydrate. Cryst. Growth Des. 2010, 10, 3340–3347. [Google Scholar] [CrossRef]
- Zellelow, A.Z.; Cox, K.A.; Fink, D.A.; Ford, C.E.; Kim, K.H.; Sours, R.E.; Swift, J.A. Doping uric acid crystals. 2. Anhydrous uric acid. Cryst. Growth Des. 2010, 10, 3348–3354. [Google Scholar] [CrossRef]
- Fink, D.A.; Sours, R.E.; Swift, J.A. Modulated uric acid growth in the presence of acridine dyes. Chem. Mater. 2003, 15, 2718–2723. [Google Scholar] [CrossRef]
- Sours, R.E.; Fink, D.A.; Swift, J.A. Dyeing uric acid crystals with methylene blue. J. Am. Chem. Soc. 2002, 124, 8630–8636. [Google Scholar] [CrossRef] [PubMed]
- Moore, F.J.; Gatewood, E.S. The action of hydrogen peroxide upon certain phenyl-substituted uric acids. J. Am. Chem. Soc. 1923, 45, 135–145. [Google Scholar] [CrossRef]
- Berreman, D.W. Optics in stratified and anisotropic media: 4 × 4-Matrix formulation. J. Opt. Soc. Am. 1972, 62, 502–510. [Google Scholar] [CrossRef]
- Wöhler, H.; Hass, G.; Fritsch, M.; Mlynski, D.A. Faster 4 × 4 matrix method for uniaxial inhomogenous media. J. Opt. Soc. Am. A 1988, 5, 1554–1557. [Google Scholar] [CrossRef]
- Azzam, R.M.A.; Bashara, N.M. Ellipsometry and Polarized Light; North Holland: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Hong, Q.; Wu, T.X.; Wu, S.T. Optical wave propagation in a cholesteric liquid crystal using the finite element method. Liquid Cryst. 2003, 30, 367–375. [Google Scholar] [CrossRef]
- St. John, W.D.; Fritz, W.J.; Lu, Z.J.; Yang, D.K. Bragg reflection from cholesteric liquid crystals. Phys. Rev. E 1995, 51, 1191–1198. [Google Scholar] [CrossRef]
- Mendoza-Galván, A.; Fernández del Río, L.; Järrendahl, K.; Arwin, H. Graded pitch profile for the helicoidal broadband reflector and left-handed circularly polarizing cuticle of the scarab beetle Chrysina chrysargyrea. Sci. Rep. 2018, 8, 6456. [Google Scholar] [CrossRef] [PubMed]
- Hunt, R.W.G.; Pointer, M.R. Measuring Color, 4th ed.; Wiley: Petaling Jaya, Malaysia, 2011. [Google Scholar]
- Azofeifa, D.E.; Arguedas, H.J.; Vargas, W.E. Optical properties of chitin and chitosan biopolymers with application to structural color analysis. Opt. Mater. 2012, 35, 175–183. [Google Scholar] [CrossRef]
- Vargas, W.E.; Azofeifa, D.E.; Arguedas, H.J. Índices de refracción de la quitina, el quitosano y el ácido úrico con aplicación en análisis de color estructural. Óptica Pura y Aplicada 2013, 46, 55–72. [Google Scholar] [CrossRef]
- Arwin, H.; Berlind, T.; Johs, B.; Järrendahl, K. Cuticle structure of the scarab beetle Cetonia aurata analyzed by regression analysis of Mueller-matrix ellipsometric data. Opt. Express 2013, 21, 22645–22656. [Google Scholar] [CrossRef] [PubMed]
- Richards, A.G. The Integument of Arthropods; University of Minnesota Press: Minneapolis, MN, USA, 1951. [Google Scholar]
- Carter, I.E.; Weir, K.; McCall, M.W. Investigation of the variation of near-circular polarization in Scarabaeoidea beetles. Mater. Today Proc. 2017, 4, 4942–4951. [Google Scholar] [CrossRef]













© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vargas, W.E.; Avendano, E.; Hernández-Jiménez, M.; Azofeifa, D.E.; Libby, E.; Solís, Á.; Barboza-Aguilar, C. Photonic Crystal Characterization of the Cuticles of Chrysina chrysargyrea and Chrysina optima Jewel Scarab Beetles. Biomimetics 2018, 3, 30. https://doi.org/10.3390/biomimetics3040030
Vargas WE, Avendano E, Hernández-Jiménez M, Azofeifa DE, Libby E, Solís Á, Barboza-Aguilar C. Photonic Crystal Characterization of the Cuticles of Chrysina chrysargyrea and Chrysina optima Jewel Scarab Beetles. Biomimetics. 2018; 3(4):30. https://doi.org/10.3390/biomimetics3040030
Chicago/Turabian StyleVargas, William E., Esteban Avendano, Marcela Hernández-Jiménez, Daniel E. Azofeifa, Eduardo Libby, Ángel Solís, and Cynthia Barboza-Aguilar. 2018. "Photonic Crystal Characterization of the Cuticles of Chrysina chrysargyrea and Chrysina optima Jewel Scarab Beetles" Biomimetics 3, no. 4: 30. https://doi.org/10.3390/biomimetics3040030
APA StyleVargas, W. E., Avendano, E., Hernández-Jiménez, M., Azofeifa, D. E., Libby, E., Solís, Á., & Barboza-Aguilar, C. (2018). Photonic Crystal Characterization of the Cuticles of Chrysina chrysargyrea and Chrysina optima Jewel Scarab Beetles. Biomimetics, 3(4), 30. https://doi.org/10.3390/biomimetics3040030