Natural Frequencies of Diatom Shells: Alteration of Eigenfrequencies Using Structural Patterns Inspired by Diatoms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Diatom-Inspired Dome Structures
2.1.1. Construction
2.1.2. Modal Analyses
2.2. Thickness Optimization of Dome Structures
2.2.1. Regularly Distributed Ribs
2.2.2. Irregularly Distributed Ribs
3. Results
3.1. Diatom-Inspired Dome Structures
3.1.1. Construction
3.1.2. Modal Analyses
- (a)
- Combs (Figure 13a)
- For models showing a constant comb size (both honeycombs and Voronoi combs): a larger comb size tends to increase the 1st eigenfrequency by about 27% (models 10 vs. 2, and 3 vs. 1)
- For models with regular and irregular combs (no fractale combs): the 1st eigenfrequency seems to be significantly higher (>25%) if the comb pattern forms the structure itself compared to comb patterns applied as ribs to a simple dome structure (models 10 vs. 35, 3 vs. 32, 4 vs. 33, and 6 vs. 34). However, for models with fractale honeycombs or Voronoi combs, applying the comb pattern as ribs to a simple dome surface shows an increase of the 1st eigenfrequency by 11% to 14% (models 36 vs. 7, and 37 vs. 12)
- Generally, smaller combs close to the model’s border and larger combs in the middle tends to increases the 1st eigenfrequency (increase of 21% for model 3 vs. 6)
- For models with a constant comb size, the comb unit geometry (regular honeycomb, irregular Voronoi, or fractale combs) seems to almost not affect the 1st eigenfrequency (deviations < 5%; models 1 vs. 2, 3 vs. 10, and 32 vs. 35)
- (b)
- Ribs (Figure 13b)
- A lower number of stiffening ribs tends to increase the 1st eigenfrequency by more than 9% (models 27 vs. 26, and 27 vs. 28)
- Placing voids in the model’s centre, especially an irregular void pattern, in combination with stiffening the model’s border apparently increases the 1st eigenfrequency, here the increase was 20% (model 39 vs. 40)
- Small geometrical adaptations that almost do not affect the mass, or that are not close to the model’s centre are likely to almost not alter the 1st eigenfrequency (models 14 vs. 23, 11 vs. 25, and 11 vs. 8)
- (c)
- Bulging (Figure 13c)
- Irregular or deformed undulating bulges seem to increase the 1st eigenfrequency by about 20% (models 18 vs. 31, and 47 vs. 30)
- The results indicate that the smaller scaled the bulging pattern, the higher the 1st eigenfrequency (increases of more than 12% for models 47 vs. 18, and 18 vs. 22)
- Small-scaled bulges close to the border that increase the stiffness in combination with an irregular embossing shape in the model’s centre tends to lead to a very high eigenfrequency, especially if the mass in the model’s centre can be reduced (1st eigenfrequency increase of 23% for model 46 vs. 45)
- The number of radial symmetric undulating segments appears to only alter the 1st eigenfrequency less than 6% (models 16 vs. 21, and 17 vs. 16)
- Small voids distributed over the whole model area seem to hardly affect the 1st eigenfrequency (model 30 vs. 48)
- (d)
- Geometrical Variations (Figure 13d)
- The results indicate that stiff borders are at least equally important to increase the freuency, so that models with stiff borders and without voids in the middle can show higher eigenfrequencies (1st eigenfrequency increase of 41% and 33% for the models 9 vs. 44 and 9 vs. 43, respectively)
3.2. Thickness Optimization of Dome Structures
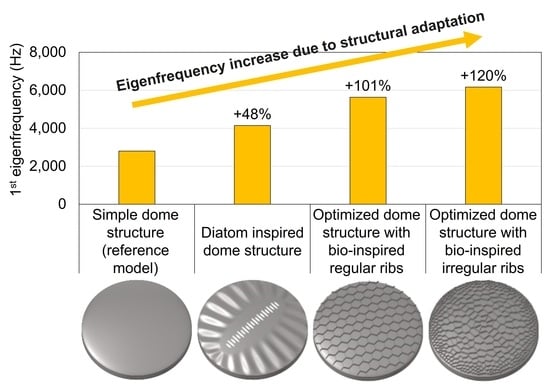
3.3. Comparison
4. Discussion
4.1. Diatom-Inspired Dome Structures
4.2. Thickness Optimization of Dome Structures
4.3. Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maier, M.; Siegel, D.; Thoben, K.D.; Niebuhr, N.; Hamm, C. Transfer of natural micro structures to bionic lightweight design proposals. J. Bionic Eng. 2013, 10, 469–478. [Google Scholar] [CrossRef]
- Pohl, G.; Nachtigall, W. Biomimetics for Architecture & Design. Nature-Analogies-Technology; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Heinrichs, A.; Frank, P.; Siegel, D.; Frank, M. Bionische Entwicklung einer additiv gefertigten A-Säulen-Verstärkung. Lightweight Des. 2017, 4, 74–81. [Google Scholar] [CrossRef]
- Andresen, S.; Meyners, N.; Thoden, D.; Körfer, M.; Hamm, C. Biologically Inspired Girder Structure for the Synchrotron Radiation Facility PETRA IV. J. Bionic Eng. 2023, 20, 1996–2017. [Google Scholar] [CrossRef]
- Breish, F.; Hamm, C.; Kienzler, R. Diatom-inspired stiffness optimization for plates and cellular solids. Bioinspir. Biomim. 2023, 18, 036004. [Google Scholar] [CrossRef] [PubMed]
- Andresen, S. Improving vibration characteristics by using bio-inspired structures. In Proceedings of the Bionik: Patente aus der Natur, Innovationspotenziale für Technologieanwendungen, 9. Bremer Bionik-Kongress, Bremen, Germany, 27–28 October 2006; Kesel, A.B., Zehren, D., Eds.; Bionik-Innovations-Centrum: Bremen, Germany, 2019. [Google Scholar]
- Andresen, S.; Bäger, A.; Hamm, C. Eigenfrequency maximisation by using irregular lattice structures. J. Sound Vib. 2020, 465, 115027. [Google Scholar] [CrossRef]
- Andresen, S. Impact of Bio-inspired Structural Irregularities on Plate Eigenfrequencies. In Proceedings of the Proceedings of the 14th International Conference on Vibration Problems. ICOVP 2019. Lecture Notes in Mechanical Engineering, Crete, Greece, 1–4 September 2019; Sapountzakis, E.J., Banerjee, M., Biswas, P., Inan, E., Eds.; Springer: Singapore, 2021; pp. 1117–1125. [Google Scholar] [CrossRef]
- Guiry, M.D. How many species of algae are there? J. Phycol. 2012, 48, 1057–1063. [Google Scholar] [CrossRef]
- Mann, D.G.; Droop, S. Biodiversity, biogeography and conservation of diatoms. In Proceedings of the Biogeography of Freshwater Algae: Proceedings of the Workshop on Biogeography of Freshwater Algae, Held During the Fifth International Phycological Congress, Qingdao, China, 26 June–2 July 1994; Springer: Berlin/Heidelberg, Germany, 1996; pp. 19–32. [Google Scholar] [CrossRef]
- Koehl, M.; Strickier, J.R. Copepod feeding currents: Food capture at low Reynolds number 1. Limnol. Oceanogr. 1981, 26, 1062–1073. [Google Scholar] [CrossRef]
- Almqvist, N.; Delamo, Y.; Smith, B.; Thomson, N.; Bartholdson, Å.; Lal, R.; Brzezinski, M.; Hansma, P. Micromechanical and structural properties of a pennate diatom investigated by atomic force microscopy. J. Microsc. 2001, 202, 518–532. [Google Scholar] [CrossRef]
- Losic, D.; Short, K.; Mitchell, J.G.; Lal, R.; Voelcker, N.H. AFM nanoindentations of diatom biosilica surfaces. Langmuir 2007, 23, 5014–5021. [Google Scholar] [CrossRef]
- Diaz Moreno, M.; Ma, K.; Schoenung, J.; Dávila, L.P. An integrated approach for probing the structure and mechanical properties of diatoms: Toward engineered nanotemplates. Acta Biomater. 2015, 25, 313–324. [Google Scholar] [CrossRef]
- Hamm, C.E.; Merkel, R.; Springer, O.; Jurkojc, P.; Maier, C.; Prechtel, K.; Smetacek, V. Architecture and material properties of diatom shells provide effective mechanical protection. Nature 2003, 421, 841–843. [Google Scholar] [CrossRef]
- Gutiérrez, A.; Guney, M.G.; Fedder, G.K.; Dávila, L.P. The role of hierarchical design and morphology in the mechanical response of diatom-inspired structures via simulation. Biomater. Sci. 2018, 6, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Topal, E.; Rajendran, H.; Zgłobicka, I.; Gluch, J.; Liao, Z.; Clausner, A.; Kurzydłowski, K.J.; Zschech, E. Numerical and experimental study of the mechanical response of diatom frustules. Nanomaterials 2020, 10, 959. [Google Scholar] [CrossRef] [PubMed]
- Cvjetinovic, J.; Luchkin, S.Y.; Perevoschikov, S.; Davidovich, N.A.; Salimon, A.I.; Bedoshvili, Y.D.; Somov, P.A.; Lagoudakis, P.; Korsunsky, A.M.; Gorin, D.A. Probing vibrational eigenmodes in diatom frustules via combined in silico computational study and atomic force microscopy experimentation. Appl. Phys. Lett. 2023, 123, 184101. [Google Scholar] [CrossRef]
- Abdusatorov, B.; Salimon, A.I.; Bedoshvili, Y.D.; Likhoshway, Y.V.; Korsunsky, A.M. FEM exploration of the potential of silica diatom frustules for vibrational MEMS applications. Sens. Actuators Phys. 2020, 315, 112270. [Google Scholar] [CrossRef]
- Gutiérrez, A.; Gordon, R.; Dávila, L.P. Deformation modes and structural response of diatom frustules. J. Mater. Sci. Eng. Adv. Technol. 2017, 15, 105–134. [Google Scholar] [CrossRef]
- Andresen, S.; Lottes, L.M.; Linnemann, S.K.; Kienzler, R. Shape adaptation of beams (1D) and plates (2D) to maximise eigenfrequencies. Adv. Mech. Eng. 2020, 12, 1687814020971903. [Google Scholar] [CrossRef]
- Yang, R.; Chen, C.; Lee, C. Bead pattern optimization. Struct. Optim. 1996, 12, 217–221. [Google Scholar] [CrossRef]
- Krog, L.A.; Olhoff, N. Optimum topology and reinforcement design of disk and plate structures with multiple stiffness and eigenfrequency objectives. Comput. Struct. 1999, 72, 535–563. [Google Scholar] [CrossRef]
- Alshabatat, N.T.; Naghshineh, K. Optimization of the natural frequencies of plates via dimpling and beading techniques. Int. J. Model. Simul. 2012, 32, 244–254. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Topology Optimization. Theory, Methods, and Applications, 2nd ed.; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2004. [Google Scholar] [CrossRef]
- Wu, J.J. Prediction of the torsional vibration characteristics of a rotor-shaft system using its scale model and scaling laws. Int. J. Mech. Mechatron. Eng. 2015, 9, 229–234. [Google Scholar]
- Zai, B.A.; Sami, S.; Khan, M.A.; Ahmad, F.; Park, M.K. Prediction of vibration characteristics in beam structure using sub-scale modeling with experimental validation. Chin. J. Mech. Eng. 2015, 28, 928–934. [Google Scholar] [CrossRef]
- Round, F.E.; Crawford, R.M.; Mann, D.G. The Diatoms. Biology & Morphology of the Genera; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Qu, Z.Q. Model Order Reduction Techniques with Applications in Finite Element Analysis; Springer: London, UK, 2004. [Google Scholar]
- Schmitz, T.L.; Smith, K.S. Mechanical Vibrations. Modeling and Measurement; Springer: New York, NY, USA; Dordrecht, The Netherlands; Berlin/Heidelberg, Germany; London, UK, 2012. [Google Scholar]
- Gross, D.; Hauger, W.; Schröder, J.; Wall, W.A.; Govindjee, S. Engineering Mechanics 3. Dynamics; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Ying, S.; Xu, G.; Li, C.; Mao, Z. Point cluster analysis using a 3D Voronoi diagram with applications in point cloud segmentation. ISPRS Int. J.-Geo-Inf. 2015, 4, 1480–1499. [Google Scholar] [CrossRef]
- Hamm, C.; Smetacek, V. Armor: Why, when, and how. In Evolution of Primary Producers in the Sea; Falkowski, P.G., Knoll, A.H., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 311–332. [Google Scholar] [CrossRef]


















| Property | Value |
|---|---|
| Young’s modulus, E (MPa) | 75,000 |
| Shear modulus, G (MPa) | 28,195 |
| Poisson’s ratio, (−) | 0.33 |
| Density, (kg ) | 2700 |
| Shell Thickness (mm) | Mass (g) | 1st Eigenfrequency (Hz) | |
|---|---|---|---|
| MIN | 0.92 | 87.00 | 660 |
| MAX | 5.51 | 87.08 | 4139 |
| AVERAGE | 1.92 | 87.02 | 2291 |
| Model Number | Rib Distribution | Comb Spacing Value/Parameter Values (mm) | Rib Height (mm) | 1st Eigenfrequency (Hz) | 1st Mode Shape |
|---|---|---|---|---|---|
| 1 | regular | 5 | 4.0 | 5621 | Mode 1 |
| 2 | regular | 8 | 4.0 | 5557 | Mode 1 |
| 3 | regular | 12 | 4.0 | 5631 | Mode 2 |
| 4 | regular | 16 | 4.0 | 5392 | Mode 2 |
| 5 | regular | 20 | 4.0 | 5176 | Mode 1 |
| 6 | regular | 25 | 4.0 | 4919 | Mode 1 |
| 7 | regular | 30 | 4.0 | 4708 | Mode 1 |
| 8 | irregular | 5 | 4.0 | 5599 | Mode 1 |
| 9 | irregular | 10 | 4.0 | 5597 | Mode 1 |
| 10 | irregular | 15 | 4.0 | 5188 | Mode 1 |
| 11 | irregular | 20 | 4.0 | 5103 | Mode X |
| 12 | irregular | GV = 5; LV = 15; | 4.0 | 5453 | Mode 1 |
| TD = 10 | |||||
| 13 | irregular | GV = 5; LV = 18; | 4.0 | 5438 | Mode 1 |
| TD = 20 | |||||
| 14 | irregular | GV = 3; LV = 8; | 4.0 | 5987 | Mode 1 |
| TD = 20 | |||||
| 15 | irregular | GV = 3; LV = 10; | 4.0 | 5927 | Mode 1 |
| TD = 20 | |||||
| 16 | irregular | GV = 3; LV = 12; | 4.0 | 5846 | Mode 1 |
| TD = 20 | |||||
| 17 | irregular | GV = 3; LV = 16; | 4.0 | 5507 | Mode 1 |
| TD = 20 | |||||
| 18 | irregular | GV = 3; LV = 8; | 4.0 | 5944 | Mode 1 |
| TD = 25 | |||||
| 19 | irregular | GV = 3; LV = 8; | 4.0 | 6011 | Mode 1 |
| TD = 30 | |||||
| 20 | irregular | GV = 3; LV = 15; | 4.0 | 5706 | Mode 1 |
| TD = 25 | |||||
| 21 | irregular | GV = 2; LV = 8; | 4.0 | 5942 | Mode 1 |
| TD = 20 | |||||
| 22 | irregular | GV = 4; LV = 8; | 4.0 | 5857 | Mode 2 |
| TD = 20 | |||||
| 23 | irregular | GV = 3; LV = 8; | 3.0 | 5649 | Mode 1 |
| TD = 30 | |||||
| 24 | irregular | GV = 3; LV = 8; | 4.5 | 6165 | Mode 1 |
| TD = 30 | |||||
| 25 | irregular | GV = 3; LV = 8; | 5.0 | 6072 | Mode 1 |
| TD = 30 |
| Property | Present Study | Cvjetinovic et al. [18] |
|---|---|---|
| Young’s modulus, E (MPa) | = 75,000 | = 15,000 |
| Density, (kg ) | = 2700 | = 2300 |
| Poisson’s ratio, (−) | 0.33 | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andresen, S.; Linnemann, S.K.; Ahmad Basri, A.B.; Savysko, O.; Hamm, C. Natural Frequencies of Diatom Shells: Alteration of Eigenfrequencies Using Structural Patterns Inspired by Diatoms. Biomimetics 2024, 9, 85. https://doi.org/10.3390/biomimetics9020085
Andresen S, Linnemann SK, Ahmad Basri AB, Savysko O, Hamm C. Natural Frequencies of Diatom Shells: Alteration of Eigenfrequencies Using Structural Patterns Inspired by Diatoms. Biomimetics. 2024; 9(2):85. https://doi.org/10.3390/biomimetics9020085
Chicago/Turabian StyleAndresen, Simone, Selina K. Linnemann, Ahmad Burhani Ahmad Basri, Oleksandr Savysko, and Christian Hamm. 2024. "Natural Frequencies of Diatom Shells: Alteration of Eigenfrequencies Using Structural Patterns Inspired by Diatoms" Biomimetics 9, no. 2: 85. https://doi.org/10.3390/biomimetics9020085
APA StyleAndresen, S., Linnemann, S. K., Ahmad Basri, A. B., Savysko, O., & Hamm, C. (2024). Natural Frequencies of Diatom Shells: Alteration of Eigenfrequencies Using Structural Patterns Inspired by Diatoms. Biomimetics, 9(2), 85. https://doi.org/10.3390/biomimetics9020085