SAXS Analysis of Magnetic Field Influence on Magnetic Nanoparticle Clusters
Abstract
:1. Introduction
2. Experimental
2.1. Sample Preparation
2.2. Measurements
3. Theoretical Background
4. Results and Discussions
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SAXS | Small-Angle X-ray Scattering |
| LNLS | Brazilian Synchrotron Light Laboratory |
References
- Papell, S.S. Low Viscosity Magnetic Fluid Obtained by the Colloidal Suspension of Magnetic Particles. U.S. Patent 3215572, 2 November 1965. [Google Scholar]
- Rosensweig, R.E.; Kaiser, R. Study of Ferromagnetic Liquid, Phase I; NTIS Rep. No. NASW-1219; NASA Office of Advanced Reseach and Technology: Washington, DC, USA, 1967.
- Rosensweig, R.E. Ferrohydrodynamics; Cambridge University Press: Cambridge, UK; London, UK, 1985. [Google Scholar]
- Beeran, A.E.; Fernandez, F.B.; Nazeer, S.S.; Jayasree, R.S.; John, A.; Anil, S.; Vellappally, S.; Al Kheraif, A.A.A.; Varma, P.R.H. Multifunctional nano manganese ferrite ferrofluid for efficient theranostic application. Colloids Surf. B Biointerfaces 2015, 136, 1089–1097. [Google Scholar] [CrossRef] [PubMed]
- Pankhurst, Q.A.; Thanh, N.T.K.; Jones, S.K.; Dobson, J. Progress in applications of magnetic nanoparticles in biomedicine. J. Phys. D Appl. Phys. 2009, 22, 224001. [Google Scholar] [CrossRef]
- Fu, Z.; Xiao, Y.; Feoktystov, A.; Pipich, V.; Appavou, M.; Su, Y.; Feng, E.; Jina, W.; Bruckel, T. Field-induced self-assembly of iron oxide nanoparticles investigated using small-angle neutron scattering. Nanoscale 2016, 8, 18541–18550. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rozynek, Z.; Jozefczak, A.; Knudsen, K.D.; Skumiel, A.; Hornowski, T.; Fossum, J.O.; Timko, M.; Kopcanshy, P.; Koneracka, M. Structuring from nanoparticles in oil-based ferrofluids. Eur. Phys. J. E 2011, 34. [Google Scholar] [CrossRef] [PubMed]
- Campi, G.; Poccia, N.; Joseph, B.; Bianconi, A.; Mishra, S.; Lee, J.; Roy, S.; Agung Nugroho, A.; Buchholz, M.; Braden, M.; et al. Direct Visualization of Spatial inhomogeneity of Spin Stripes Order in La1.72Sr0.28NiO4. arXiv 2019, arXiv:1905.02124. [Google Scholar]
- Campi, G.; Bianconi, A. Evolution of Complexity in Out-of-Equilibrium Systems by Time-Resolved or Space-Resolved Synchrotron Radiation Techniques. Condens. Matter 2019, 4, 32. [Google Scholar] [CrossRef]
- Wandersman, E.; Chushkin, Y.; Dubois, E.; Dupuis, V.; Robert, A.; Perzynski, R. Field induced anisotropic cooperativity in amagnetic colloidal glass. Soft Matter 2015, 11, 7165. [Google Scholar] [CrossRef] [PubMed]
- Myrovali, E.; Maniotis, N.; Makridis, A.; Terzopoulou, A.; Ntomprougkidis, V.; Simeonidis, K.; Sakellari, D.; Kalogirou, O.; Samaras, T.; Salikhov, R.; et al. Arrangement at the nanoscale Effect on magnetic particle hyperthermia. Sci. Rep. 2016, 6, 37934. [Google Scholar] [CrossRef]
- Abenojar, E.C.; Wickramasinghe, S.; Bas-Concepcion, J.; Samia, A.C.S. Structural effects on the magnetic hyperthermia properties of iron oxide nanoparticles. Prog. Nat. Sci. Mater. Int. 2016, 26, 440–448. [Google Scholar] [CrossRef] [Green Version]
- Serantes, D.; Simeonidis, K.; Angelakeris, M.; Chubykalo-Fesenko, O.; Marciello, M.; Del Puerto Morales, M.; Baldomir, D.; Martinez-Boubeta, C. Multiplying Magnetic Hyperthermia. Response by Nanoparticle Assembling. J. Phys. Chem. C 2014, 118, 5927–5934. [Google Scholar] [CrossRef]
- Martinez-Boubeta, C.; Simeonidis, K.; Makridis, A.; Angelakeris, M.; Iglesias, O.; Guardia, P.; Cabot, A.; Yedra, L.; Estradé, S.; Peiró, F.; et al. Learning from nature to improve the heat generation of iron-oxide nanoparticles for magnetic hyperthermia applications. Sci. Rep. 2013, 3, 1652. [Google Scholar] [CrossRef] [PubMed]
- Mehdaoui, B.; Tan, R.P.; Meffre, A.; Carrey, J.; Lachaize, S.; Chaudret, B.; Respaud, M. Increase of magnetic hyperthermia efficiency due to dipolar interactions in low-anisotropy magnetic nanoparticles: Theoretical and experimental results. Phys. Rev. B 2013, 87, 174419. [Google Scholar] [CrossRef]
- Bañobre-López, M.; Teijeiro, A.; Rivas, J. Magnetic nanoparticle-based hyperthermia for cancer treatment. Rep. Pract. Oncol. Radiother. 2013, 18, 397–400. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Beaucage, G.; Schaefer, D.W. Structural studies of complex systems using small-angle scattering: A unified Guinier/power-law approach. J. Non-Cryst. Solids 1994, 172–174, 797–805. [Google Scholar] [CrossRef]
- Beaucage, G. Approximations Leading to a Unified Exponential/Power-Law Approach to Small-Angle Scattering. J. Appl. Cryst. 1995, 28, 717. [Google Scholar] [CrossRef]
- Beaucage, G. Small-Angle Scattering from Polymeric Mass Fractals of Arbitrary Mass-Fractal Dimension. J. Appl. Cryst. 1996, 29, 134. [Google Scholar] [CrossRef]
- Beaucage, G. Determination of branch fraction and minimum dimension of mass-fractal aggregates. Phys. Rev. E 2004, 70, 031401. [Google Scholar] [CrossRef] [Green Version]
- Beaucage, G.; Kammler, H.K.; Pratsinis, S.E. Particle size distributions from small-angle scattering using global scattering functions. J. Appl. Cryst. 2004, 37, 523. [Google Scholar] [CrossRef]
- Paula, F.L.O.; Depeyrot, J.; Fossum, J.O.; Tourinho, F.A.; Aquino, R.; Knudsen, K.D.; da Silva, G.J. Small-angle X-ray and small-angle neutron scattering investigations of colloidal dispersions of magnetic nanoparticles and clay nanoplatelets. J. Appl. Cryst. 2007, 40, 269–273. [Google Scholar] [CrossRef]
- Martins, F.H.; da Silva, F.G.; Paula, F.L.O.; Gomes, J.A.; Aquino, R.; Mestnik-Filho, J.; Bonville, P.; Porcher, F.; Perzynski, R.; Depeyrot, J. Local Structure of Core-Shell MnFe2O4+δ Based Nanocrystals: Cation Distribution and Valence States of Manganese Ions. J. Phys. Chem. C 2017, 121, 8982–8991. [Google Scholar] [CrossRef]
- Paula, F.L.O.; da Silva, G.J.; Aquino, R.; Depeyrot, J.; Fossum, J.O.; Knudsen, K.; Tourinho, F.A. Gravitational and Magnetic Separation in Self-Assembled Clay-Ferrofluid Nanocomposites. Braz. J. Phys. 2009, 39, 163–170. [Google Scholar] [CrossRef]
- Castro, L.L.; da Silva, M.; Bakuzis, A.; Miotto, R. Aggregate formation on polydisperse ferrofluids: A Monte Carlo analysis. J. Magn. Magn. Mater. 2005, 293, 553–558. [Google Scholar] [CrossRef]
- Vanessa, P.; Cabreira, R.G.; Gomide, G.S.; Coppola, P.; Silva, F.G.; Paula, F.L.O.; Perzynski, R.; Goya, F.G.; Aquino, R.; Depeyrot, J. Core/Shell Nanoparticles of Non-Stoichiometric Zn-Mn and Zn-Co Ferrites as Thermosensitive Heat Sources for Magnetic Fluid Hyperthermia. J. Phys. Chem. C 2018, 122, 3028. [Google Scholar] [CrossRef]
- Tourinho, F.A.; Franck, R.; Massart, R.; Perzynski, R. Synthesis and magneitc properties of managanese and cobalt ferrite ferrite ferrofluids. Prog. Colloid Polym. Sci. 1989, 79, 128–134. [Google Scholar]
- Tourinho, F.A.; Franck, R.; Massart, R. Aqueous ferrofluids based on manganese and cobalt ferrites. J. Mater. Sci. 1990, 25, 3249–3254. [Google Scholar] [CrossRef]
- Gomes, J.A.; Sousa, M.H.; Tourinho, F.A.; Aquino, R.; Depeyrot, J.; Dubois, E.; Perzynski, R. Synthesis of Core-Shell Ferrite Nanoparticles for Ferrofluids: Chemical and Magnetic Analysis. J. Phys. Chem. C 2008, 112, 6220–6227. [Google Scholar] [CrossRef]
- Zaioncz, S.; Dahmouche, K.; Soares, B.G. SAXS Characterization of New Nanocomposites Based on Epoxy Resin/Siloxane/MMA/Acrylic Acid Hybrid Materials. Macromol. Mater. Eng. 2010, 295, 243–255. [Google Scholar] [CrossRef]
- Beaucage, G.; Ulibarri, T.; Black, E.P.; Schaefer, D.W. Hybrid Organic-Inorganic Composites; Mark, J.E., Lee, C.Y.-C., Bianconi, P.A., Eds.; ACS Symposium Series 585; American Chemical Society: Washington, DC, USA, 1985; p. 97. [Google Scholar]
- Svergun, D.I.; Koch, M.H.; Timmins, P.A.; May, R.P. Small Angle X-Ray and Neutron Scattering from Solutions of Biological Macromolecules; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Moreira, A.F.L.; Paula, F.L.O.; Depeyrot, J. Evidence of Structural Distortions in Mixed Mn-Zn ferrite. IOSR J. App. Phys. 2019, 11, 36–44. [Google Scholar] [CrossRef]
- Gomes, J.A.; Azevedo, G.M.; Depeyrot, J.; Mestnik-Filho, J.; Paula, F.L.O.; Tourinho, F.A.; Perzynski, R. Structural, Chemical, and Magnetic Investigations of Core-Shell Zinc Ferrite Nanoparticles. J. Phys. Chem. C 2012, 116, 24281–24291. [Google Scholar] [CrossRef]
- Available online: http://www.esrf.eu/computing/scientic/FIT2D (accessed on 21 July 2014).
- Mériguet, G.; Cousin, F.; Dubois, E.; Boué, F.; Cebers, A.; Farago, B.; Perzynski, R. What Tunes the Structural Anisotropy of Magnetic Fluids under a Magnetic Field? J. Phys. Chem. B 2006, 110, 4378–4386. [Google Scholar] [CrossRef]
- Robbes, A.S.; Cousin, F.; Meneau, F.; Dalmas, F.; Boué, F.; Jestin, J. Nanocomposite Materials with Controlled Anisotropic Reinforcement Triggered by Magnetic Self-Assembly. Macromolecules 2011, 44, 8858–8865. [Google Scholar] [CrossRef]
 ) log-normal distribution, and (b) Reduced magnetization of (
) log-normal distribution, and (b) Reduced magnetization of (  ) sample as function of the applied magnetic filed. The solid line (
) sample as function of the applied magnetic filed. The solid line (  ) is the fit to the data using the Langevin formalism.
) is the fit to the data using the Langevin formalism.
 ) log-normal distribution, and (b) Reduced magnetization of (
) log-normal distribution, and (b) Reduced magnetization of (  ) sample as function of the applied magnetic filed. The solid line (
) sample as function of the applied magnetic filed. The solid line (  ) is the fit to the data using the Langevin formalism.
) is the fit to the data using the Langevin formalism.

 ) unified Beaucage expression described in the text. Contribution of the (
) unified Beaucage expression described in the text. Contribution of the (  ) Guinier and (
) Guinier and (  ) components related to the first level of the structure corresponding to the largest object in the dispersion, (
) components related to the first level of the structure corresponding to the largest object in the dispersion, (  ) Guinier and (
) Guinier and (  ) Porod components referring to the second structure level are relative to the isolated NPs, and (
) Porod components referring to the second structure level are relative to the isolated NPs, and (  ) is the structure factor. (a) scattering curve without external field application; (b) scattering curve obtained in the integration of the 2D pattern in the direction parallel to the magnetic field; (c) scattering curve perpendicular to the magnetic field.
) is the structure factor. (a) scattering curve without external field application; (b) scattering curve obtained in the integration of the 2D pattern in the direction parallel to the magnetic field; (c) scattering curve perpendicular to the magnetic field.
 ) unified Beaucage expression described in the text. Contribution of the (
) unified Beaucage expression described in the text. Contribution of the (  ) Guinier and (
) Guinier and (  ) components related to the first level of the structure corresponding to the largest object in the dispersion, (
) components related to the first level of the structure corresponding to the largest object in the dispersion, (  ) Guinier and (
) Guinier and (  ) Porod components referring to the second structure level are relative to the isolated NPs, and (
) Porod components referring to the second structure level are relative to the isolated NPs, and (  ) is the structure factor. (a) scattering curve without external field application; (b) scattering curve obtained in the integration of the 2D pattern in the direction parallel to the magnetic field; (c) scattering curve perpendicular to the magnetic field.
) is the structure factor. (a) scattering curve without external field application; (b) scattering curve obtained in the integration of the 2D pattern in the direction parallel to the magnetic field; (c) scattering curve perpendicular to the magnetic field.
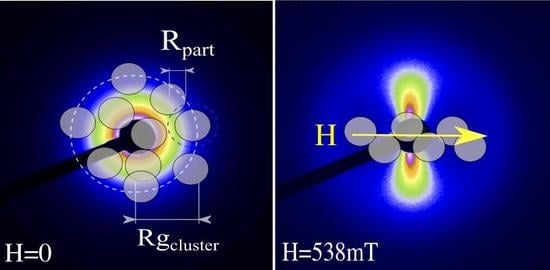
 ) corresponding to the Fourier transform to the Small Angle X-ray Scattering (SAXS) curves and the schematic drawing of the spatial configuration of the NPs, taking into account the information obtained by the Beaucage model and the curves of and the theoretical radius of gyration (, Equation (7b); , Equation (6b) is and the theoretical distance calculated with and without field; determination the size of the scattered object, that is the average of the scatter object; and is the number of NPs in the cluster with and without field; is the radius of the gyration): (a) H = 0 T; (b) with field, the formation of chains of particles with a mean inter-cluster distance of ∼ 181 Å.
) corresponding to the Fourier transform to the Small Angle X-ray Scattering (SAXS) curves and the schematic drawing of the spatial configuration of the NPs, taking into account the information obtained by the Beaucage model and the curves of and the theoretical radius of gyration (, Equation (7b); , Equation (6b) is and the theoretical distance calculated with and without field; determination the size of the scattered object, that is the average of the scatter object; and is the number of NPs in the cluster with and without field; is the radius of the gyration): (a) H = 0 T; (b) with field, the formation of chains of particles with a mean inter-cluster distance of ∼ 181 Å.
 ) corresponding to the Fourier transform to the Small Angle X-ray Scattering (SAXS) curves and the schematic drawing of the spatial configuration of the NPs, taking into account the information obtained by the Beaucage model and the curves of and the theoretical radius of gyration (, Equation (7b); , Equation (6b) is and the theoretical distance calculated with and without field; determination the size of the scattered object, that is the average of the scatter object; and is the number of NPs in the cluster with and without field; is the radius of the gyration): (a) H = 0 T; (b) with field, the formation of chains of particles with a mean inter-cluster distance of ∼ 181 Å.
) corresponding to the Fourier transform to the Small Angle X-ray Scattering (SAXS) curves and the schematic drawing of the spatial configuration of the NPs, taking into account the information obtained by the Beaucage model and the curves of and the theoretical radius of gyration (, Equation (7b); , Equation (6b) is and the theoretical distance calculated with and without field; determination the size of the scattered object, that is the average of the scatter object; and is the number of NPs in the cluster with and without field; is the radius of the gyration): (a) H = 0 T; (b) with field, the formation of chains of particles with a mean inter-cluster distance of ∼ 181 Å.
| Rg1 [Å] | P1 | Rg2 [Å] | P2 | k | ξ [Å] | Nclust | |
|---|---|---|---|---|---|---|---|
| 105 | 2.7 | 46 | 3.95 | - | - | ∼10 | |
| 81.5 | 2.79 | 45 | 4.00 | - | - | ∼5.3 | |
| 57.5 | 2.3 | 45 | 3.85 | 2.01 | 181 | ∼1.8 |
| [Å] | [Å] | [Å] | [Å] | |
|---|---|---|---|---|
| 210 | 90 | 103.2 | 105 | |
| ‖ | 160 | 74 | 84.0 | 53 |
| ⊥ | 90 | 51 | 58.2 | 37 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paula, F.L.d.O. SAXS Analysis of Magnetic Field Influence on Magnetic Nanoparticle Clusters. Condens. Matter 2019, 4, 55. https://doi.org/10.3390/condmat4020055
Paula FLdO. SAXS Analysis of Magnetic Field Influence on Magnetic Nanoparticle Clusters. Condensed Matter. 2019; 4(2):55. https://doi.org/10.3390/condmat4020055
Chicago/Turabian StylePaula, Fábio Luís de Oliveira. 2019. "SAXS Analysis of Magnetic Field Influence on Magnetic Nanoparticle Clusters" Condensed Matter 4, no. 2: 55. https://doi.org/10.3390/condmat4020055
APA StylePaula, F. L. d. O. (2019). SAXS Analysis of Magnetic Field Influence on Magnetic Nanoparticle Clusters. Condensed Matter, 4(2), 55. https://doi.org/10.3390/condmat4020055