Stochastic Kinematic Process Model with an Implemented Wear Model for High Feed Dry Grinding

Abstract

This paper considers heavy duty grinding with resin bonded corundum grinding wheels and without lubrication and cooling. A vertical turning machine redesigned to a grinding machine test bench with a power controlled grinding spindle is used in all of the experiments, allowing high tangential table feed rates up to 480 m/min. This special test-rig emulates the railway grinding usually done by a railway grinding train. The main test-rig components are presented and the resulting kinematics of the experimental set-up is described. A stochastic kinematic grinding model is presented. A wear model that is based on the kinematic description of the grinding process is set up. Grain breakage is identified as the main wear phenomenon, initiated by grain flattening and micro-splintering. The wear model is implemented into the stochastic kinematic modelling. The workpiece material side flow and spring back are considered. The simulation results are validated experimentally. The workpiece surface roughness is compared and a good agreement between simulation and experiment can be found, where the deviation between the experiment and the simulation is less than 15% for single-sided contact between the grinding wheel and the workpiece. Higher deviations between simulation and experiment, up to 24%, for double-sided contact is observed.

1. Introduction

Three important global trends of manufacturing technology in recent years were observed: moving towards increasing performance in material removal rate, higher resulting surface quality, and the reduction of coolant consumption. Chip transport from the cutting zone, cooling and lubrication are the main tasks of the coolant. Environmental impact, costs, swarf, recycling, and negative effects on the machine operator stand in contrast to the previously mentioned advantages. Grinding is often used for finishing applications to generate smooth surfaces with high integrity and low form deviations, but grinding is also yet increasingly challenging other manufacturing technologies such as high-speed or high-performance milling and turning. The implementation of high performance machining processes in general have become increasingly significant among cutting processes and could already modify many industrial manufacturing process chains by substituting one or more machining steps, and thus save cost.

As stated by Bhaduri and Chattopadhyay [1], but also by Kopac and Krajnik [2], high quality parts require high-performance grinding technologies when considering not only superior surface finish and high removal rate. The literature classifies high performance grinding not clearly distinguishable from conventional grinding and covers different grinding techniques such as: High Speed Grinding (HSG), High Efficiency Deep Grinding (HEDG), Speed-Stroke Grinding, High-Performance Surface Peel Grinding, High Work Speed Grinding, High Efficiency Grinding, Heavy Duty Grinding, and Creep Feed Grinding (CFG) [2,3,4,5,6,7,8,9,10,11]. All of these grinding techniques are used with metalworking fluids contrasting to the dry grinding process presented here.

Linke [12] gave in her review a broad overview on the recent grinding wheel wear examinations and modelling and classified four main wear mechanisms: grain surface layer wear, grain splintering, grain-bond-interface wear, and bond wear. Linke [12] distinguished between micro wear where cutting edge sharpness is lost and macro wear as loss of tool profile.

Jiang et al. [13] introduced a three-dimensional (3D) model predicting the surface roughness when considering wear and dressing effects indicating dressing as the most influential parameter. A kinematic simulation predicting the surface roughness from Liu et al. [14] modelled three different abrasive grain shapes and ductile and brittle fracture components by a single point diamond dressing tool. Jiang et al. [13,14] judged dressing to be the most influential parameter on the predicted surface roughness and grain shapes do not affect the resulting surface roughness. A stochastic process model of abrasive wear, which is based on the Poisson distribution of the wear phenomenon, was presented by Kacalak, Kasprzyk and Krzyżyński [15]. Meng and Ludema [16] presented 28 different erosion wear equations from the literature having surveyed 5466 different papers. The synthesis of those appears impossible to them.

In many dry grinding applications, resin bonded grinding wheels are used due to their self-sharpening ability, cool cut, and damping capability. In this work, the high-performance dry grinding process for surface face grinding with resin bonded corundum grinding cup wheels is analysed at high feed speeds. Especially, the self-sharpening effect is analysed. An analytical wear model considering grain failure phenomena is introduced.

2. Experimental Methods

The same test-rig as described in [17] is used. The following equipment is used for all experiments: vertical lathe SEDIN 1525 with 20 kW grinding spindle typical in rail grinding, 3D-dynamometer Kistler 9366CC, roughness measuring system Taylor Hobson Talysurf, profile, and waviness measurement sensor Micro Epsilon ILD 2300-10LL are used.

A detailed view of the experimental set-up is given in Figure 1. The marked tilt angle is adjusted with a hydraulic cylinder and can be positioned in a positive and negative direction within ±15°. The grinding wheel is clamped from outside with one fixed and two movable chuck jaws. The grinding spindle is connected directly with the cover plate of the Kistler force measuring platform. This guarantees the coordinate system conforms with force measurements without the need of coordinate transformation. The axial movement of the grinding spindle and the adjustment of depth of cut a_p during the process are performed with the pneumatic cylinder mounted behind the spindle. Two pillars guide the traverse with the spindle. The exact adjustment of the depth of cut is not possible due to the power controlled spindle support that is used in railway grinding. Force control is typical also for other high-performance dry grinding applications. The target current for the electric engine is set and the pressure is continuously adjusted during the process in the pneumatic cylinder. The tilt angle is adjusted with the hydraulic cylinder and the grinding spindle is guided on two milled slides. The ring-like workpiece is placed on the rotary table that is fixed by four chuck jaws. The whole grinding spindle construction is mounted in a frame. This frame guarantees the required stiffness and strength for the process forces and torques. A laser sensor mounted on the right-hand column is used for the surface measurements.

The cutting speed during all of the experiments is kept constant at 47 m/s at the outer circumference of the grinding wheel and the feed rate of the workpiece is 120 m/min. A resin bonded corundum grinding wheel with comparatively coarse mesh 20 is applied in the experiments. All of the experiments are carried out without metalworking fluid. Workpiece material used is 58CrMoV4 with hardness of 26 HRC. A 6 mm wide facet is ground in all of the experiments performed, however the workpiece could be turned prior to any experiment to the desired width.

Tilting the whole grinding spindle around the y-axis, as shown in Figure 2, adjusts the tilt angle while the approach angle of the grinding unit is connected to rotation around the x-axis.

Approach angle and tilt angle can be adjusted only in correlation to each other. A typical kinematic interaction between the grinding wheel and the workpiece is a single-sided contact. For the tilt angle −1.5°, the corresponding approach angle reaches zero leading to a dual-sided contact of the grinding wheel. This fundamental kinematic difference depending on the tilt angle is shown in Figure 3. Different surface patterns on the workpiece can be observed for both kinematic situations as shown later. Additionally, the self-sharpening behaviour for the dual-sided contact is significantly lowered due to the pressure being split on the two areas. Material removal rate and grinding wheel wear change between both kinematic situations.

3. Modelling

3.1. Stochastic Process Model

Based on the kinematic simulation presented in [17,18,19] a kinematic model with implemented wear model is developed for resin bonded grinding wheels. The general scheme of the stochastic process simulation with its main steps is shown in Figure 4.

The main input of the simulation is the grinding wheel geometry. Its generation is presented and follows in six steps: the generation of the basic grain form, the modification of the grain shape, the grain density definition, the extraction of the cutting profile, the positioning of the grain at the grinding wheel surface, and the height distribution of the grain. The grinding wheel macro geometry is defined by a circle formula. For abrasive grains modelled, five basic forms: cuboid, triangular prism, two triangular pyramid, and dodecahedron are defined. These are re-shaper by edge and corner fracture. This shape modification leads to a large amount of different abrasive grains corresponding with the real grinding wheel, where crushed corundum abrasive grains are used. The abrasive grain density is estimated experimentally leading and used as input for the grinding wheel generation. For the abrasive grain height distribution, a triangular distribution delivers the most accurate results, compared with uniform and normal distribution, and it is used in the grinding wheel topography modelling. The resulting modelled grinding wheel topography is then compared with the topography of the grinding wheel used experimentally by Abbott-Firestone curve. A good agreement can be found as shown in Figure 5. The deviation towards the higher profile ratio is due to the modelled grinding wheel, where only one layer of the abrasive grains is taken into account and the modelling concentrates on the cutting edge space that comes into contact with the material. The deviation in the valleys of the grinding wheel due to the approach of monolayer does not play any role for the process. The workpiece geometry is meshed with nodes in radial and tangential direction. The nodes can be chosen arbitrarily. In the meshed workpiece geometry, the resulting penetration between workpiece and grinding wheel grains is saved as a surface roughness. The result quality is directly dependent on node quantity.

Process parameters that are used in the experiment and listed in the previous section are used also in the simulation. The kinematic description used in the simulation is taken from [17].

After the definition of all the input parameters from Figure 4, including the grinding wheel, the kinematic simulation can be performed. Abrasive grains, which cannot be in contact with the workpiece, are deleted and only possible kinematic active grains are used for further calculation. This allows, particularly for small cutting depths, a huge reduction of computational time.

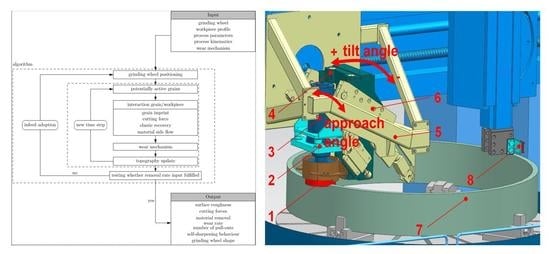
In the simulation an ideal grinding wheel shape is loaded. According to the defined approach angle, the geometry needs to be adapted. The dressed grinding wheel geometry is determined by the contact points of this idealised grinding wheel with the workpiece profile. All of the cutting points between the grinding wheel zero plane at outer and inner wheel diameter and between the workpiece profile need to be found. The approach angle can be gained by contact point height difference at the inner and outer grinding wheel diameter. In Figure 6, possible contact points are shown for grinding process where the dressing angle $\mathsf{\alpha }$ is defined.

The positioning vector of the contact point can be calculated in the workpiece and grinding wheel coordinate system. Transforming both positioning vectors in the global coordinate system and equalising them, an equation for each contact point can be defined. A cutting point on the grinding wheel surface follows according to the equation:

$${\underset{\_}{R}}_{0P,SS}={\underset{\_}{R}}_{0B}+{\underset{\_}{\underset{\_}{A}}}_{0B}\cdot {\underset{\_}{R}}_{BC}+{\underset{\_}{\underset{\_}{A}}}_{0B}\cdot {\underset{\_}{\underset{\_}{A}}}_{BC}\cdot \left({\underset{\_}{R}}_{CD}+{\underset{\_}{R}}_{DP}\right)$$

(1)

where the SS subscript indicates that point P is the cutting point from a grinding wheel point of view. R_0P,SS is the connecting vector between an arbitrary point P at the grinding wheel surface and the origin of the coordinate system indicated in Figure 6. R_0B is the connecting vector from the origin to the grinding wheel centre, R_BC is the connecting vector from grinding wheel centre to the tilting point, R_CD is the connecting vector from the tilting point to the already tilted centre of the grinding wheel, and R_DP is the connecting vector from the tilted grinding wheel centre to the arbitrary point on the grinding wheel surface P. The nomenclature of the vector is as follows: subscript describes the connection between two points in a coordinate system. $\underset{\_}{\underset{\_}{A}}$_0B and $\underset{\_}{\underset{\_}{A}}$_BC are then transformation matrices defined as:

$${\underset{\_}{\underset{\_}{A}}}_{0B}=\left(\begin{array}{ccc}\cos \left(\beta -{\beta }_0\right)& -\sin \left(\beta -{\beta }_0\right)& 0\\ \sin \left(\beta -{\beta }_0\right)& \cos \left(\beta -{\beta }_0\right)& 0\\ 0& 0& 1\end{array}\right)$$

(2)

and

$${\underset{\_}{\underset{\_}{A}}}_{BC}=\left(\begin{array}{ccc}\cos {\mathsf{\Omega }}_K& \sin {\mathsf{\Omega }}_A\sin {\mathsf{\Omega }}_K& \cos {\mathsf{\Omega }}_A\sin {\mathsf{\Omega }}_K\\ 0& \cos {\mathsf{\Omega }}_A& -\sin {\mathsf{\Omega }}_A\\ -\sin {\mathsf{\Omega }}_K& \sin {\mathsf{\Omega }}_A\cos {\mathsf{\Omega }}_K& \cos {\mathsf{\Omega }}_A\cos {\mathsf{\Omega }}_K\end{array}\right)$$

(3)

where Ω_A is the approach angle and Ω_K is the tilt angle. The transformation matrix $\underset{\_}{\underset{\_}{A}}$_0B describes the rotation of the local reference system $\mathrm{B}$ to the global coordinate system and $\underset{\_}{\underset{\_}{A}}$_BC is responsible for the adjustment of both, the tilt and approach angle.

The interaction between a pre-ground workpiece and a single grain is shown in Figure 7. From the irregular cross section in cutting speed direction multiple overlaps with the cutting surface of the grain might arise.

For every polygon, the cutting area can be calculated and summed up to a total cutting area for each abrasive grain. This is used then as input for the force calculation. To calculate the force for the whole grinding wheel, information about the force acting points for each grain is necessary. It is assumed that this acting point is in the centre of gravity of the respective cutting area. The radial position r and height position h of the centre of gravity are calculated with respect to the grinding wheel referential plane as:

$$r_t=\frac{1}{6\cdot A_t}\cdot {\displaystyle \sum _{i=1}^{i-1}\left[r\left(i\right)+r\left(i+1\right)\right]}\cdot \left[\left(h\left(i\right)-h\left(i+1\right)\right)\cdot \left(r\left(i\right)\cdot r\left(i-1\right)\right)\right]$$

(4)

$$h_t=\frac{1}{6\cdot A_t}\cdot {\displaystyle \sum _{i=1}^{i-1}\left[h\left(i\right)+h\left(i+1\right)\right]}\cdot \left[\left(h\left(i\right)-h\left(i+1\right)\right)\cdot \left(r\left(i\right)\cdot r\left(i-1\right)\right)\right]$$

(5)

A_t is the partial polygon area from the intersection between the abrasive grain and the workpiece. The centre of gravity can be then calculated from the partial polygon areas as:

$$r=\frac{1}{A}\cdot {\displaystyle \sum _{j=1}^i{r}_t\cdot A_t}$$

(6)

$$h=\frac{1}{A}\cdot {\displaystyle \sum _{j=1}^i{h}_t\cdot A_t}$$

(7)

The cutting force can be calculated according to an equation similar to the Kienzle equation as:

$$F_c=k_{c1,1}\cdot A_{cut}(t)$$

(8)

where k_c1,1 is the experimentally evaluated specific force and A represents the abrasive grain area that is engaged with the workpiece and is orthogonal to the cutting direction. The force magnitude delivered by the adapted Kienzle equation needs to be complemented by its direction. From the 3D abrasive grain geometry, as described in [17], the orthogonal cross-sectional cutting line is derived. In addition to this, the projection of all other grain faces in contact with the workpiece on the orthogonal cutting line is calculated. Each of these projected faces has its normal vector associated with it. This allows the 3D abrasive grain geometry simplification without losing information. Combining these projected normal vectors for one abrasive grain gives a resulting force direction on one abrasive grain:

$${\underset{\_}{F}}_i={\displaystyle \sum _{i=1}^{i_{\max }}\frac{v_i}{v_t}}\cdot \underset{\_}{n_i}$$

(9)

where i_max is the total number of projected normal faces of one cutting grain, v_i is the volume extracted by the single face i, v_t is the total volume extracted by the grain in the given time step, and n_i is the normal vector associated with the face i. This resulting force can be split into the cutting force F_c, showing in the direction of the cutting speed and the normal force F_N being perpendicular to the cutting force.

The resulting cutting force for the whole grinding wheel is then the sum of all the partial forces acting:

$${\underset{\_}{F}}_c={\displaystyle \sum _{i=0}^n{\underset{\_}{F}}_{ci}}$$

(10)

The normal forces are then calculated as:

$$F_N=\frac{F_c}{\mu }$$

(11)

where the friction coefficient μ = 0.3 is estimated from the experiment.

As a power controlled spindle is used in the experiment, the proper depth of cut needs to be calculated. As explained above, the nominal current of the grinding spindle electric engine is set and compared with the actually measured current. The measured current is a result of the contact condition between the grinding wheel and the workpiece, and thus of the axial force on the grinding wheel exerted by a pneumatic cylinder. This force needs to be counterbalanced by the sum of the penetration forces of the individual active grains. With increasing force, the amount of active abrasive grains and their penetration depth increases and the current rises. For each height of the grinding wheel, the penetration depth of every single stochastically distributed, oriented, and shaped active grain can be calculated, and thus the forces can be derived from the single grain force model. Iteration is then performed until the sum of the individual grain forces equals the externally applied axial force, pneumatic, and dead weight force, on the spindle. The resulting experimentally measured vertical force is used in the simulation as the nominal value. An estimate of the number of active abrasive grains is known, and thus the force can be distributed among them. The initial grinding wheel position is defined as one where the highest abrasive grain touches the workpiece surface. The simulation is performed with a stepwise increase of the depth of the cut by the amount of one percent of an average abrasive grain diameter, as schematically shown in Figure 8. If the sum of all vertical forces of the individual abrasive grains in contact with the workpiece is equal to the nominal, experimental, force value, then the simulation continues at this depth of cut. As the propagated wear of the abrasive grain can lead to an unbalance between the nominal and the real vertical force, the depth of cut needs to be adjusted iteratively. In case an abrasive grain is completely worn and is out of contact, the resulting forces are lowered and the depth of cut needs to be increased again. The worn abrasive grain is in contact again and, additionally, new abrasive grains are potentially cutting. The stepwise increase or decrease of the depth of cut is done until the balance between the nominal and simulated force is found again. When the equilibrium between the simulated and experimental forces is reached, the calculation of the workpiece surface roughness can start.

The workpiece material side flow and the workpiece spring back are modelled to determine the ground profile. Based on Li [20], the side burr is modelled as a triangular ridge accompanying the scratch. It is described by its base b and height h. Li [20] claims that the side flow is not significantly affected by the abrasive grain rake angle and that the triangle base b is three times its height h which gives for h:

$$h=1.27\cdot A_{cut}{}^{0.29}\cdot v_g^{-0.87}$$

(12)

where v_g is the grain velocity in m/s and A_cut the area of the cutting profile being engaged with the workpiece in m².

The material spring back model is based on a publication by Shaw and DeSalvo [21] about hardness measurements. They claim that the material actively reacting on the imposed pressure on the surface is maximum ten times the penetration of the indenter. The elastic material displacement can be calculated as:

$$\Delta l=\frac{F\cdot l}{E\cdot A}$$

(13)

where Δl is the elastic material displacement, F is the normal force acting on the workpiece surface, E is the elastic modulus, l is the material depth responding to the abrasive grain penetration, and A is the workpiece area responding to the applied pressure. The force from experiment is in the range from 1200 to 1400 N. This force is then divided between all of the active abrasive grains and an average force is attributed to a single active grain. The length l is attributed to the workpiece material amount, which answers to the pressure applied.

3.2. Wear Modelling

The main wear mechanism identified as responsible for the geometry change of the grinding wheel is a fracture of the abrasives. This is a result of an initial abrasive grain flattening causing force increase until fracture.

Grain fracture is observed experimentally, after reaching steady state, and is mainly in a vertical direction—the direction of the normal force. The vertical component comes from the high normal pressure due to the spindle weight and the power control. The horizontal component is resulting from the cutting process and thus the spindle torque.

The main parameters influencing the grinding wheel wear are the cutting force, the cutting speed, and the contact temperature. With increasing active time of the abrasive grain, the wear is propagating until a critical load is reached. This behaviour can be expressed as:

$$\frac{dW}{dt}=K·F_c(t)\cdot v_c\cdot e^{-\frac{B}{T_{grind}}}$$

(14)

where dW/dt is the wear rate in mm/s, K is the wear factor, B is a constant coming from the Arrhenius equation, where activating energy and universal gas constant are considered, F_c is the cutting force, v_c is the cutting speed for the abrasive grain, and T_grind is the contact temperature between the abrasive grain and the workpiece. Evaluation of the wear factor K is based on an experimental macroscopic wear evaluation.

The cutting area A_cut in Equation (8) changes with the wear progress W(t) and can be calculated as:

$$A_{cut}(h(t))=\left[(h_0-W(t)\right]\cdot b$$

(15)

where h₀ is the initial abrasive grain height and b is the abrasive grain width assumed to be constant during the whole cutting process as shown in Figure 9.

The cutting force also depends on the cutting edge condition, which by wear becomes duller. This leads to cutting force increase and can be considered by the introduction of a cutting edge dulling factor M. The force can be then calculated as:

$$F_c=k_{c1,1}\cdot \left(1+M\cdot \frac{W(t)}{h_0}\right)\cdot A_{cut}(h(t))$$

(16)

With the cutting area being calculated according to Equation (15), the cutting force can be calculated as:

$$F_c=k_{c1,1}\cdot b\cdot \left(h_0-W(t)+M\cdot W(t)-M\cdot \frac{W^2(t)}{h_0}\right)$$

(17)

Substituting Equation (17) into Equation (14) leads to:

$$\frac{dW}{dt}=K\cdot v_c\cdot e^{\left(-\frac{B}{T_{grind}}\right)}\cdot k_{c1,1}\cdot b\cdot \left(h_0-W(t)+M\cdot W(t)-M\cdot \frac{W^2(t)}{h_0}\right)$$

(18)

The whole term in front of the bracket is a constant in time and is renamed by H leading to:

$$\frac{dW}{dt}=H\cdot \left(h_0-W(t)+M\cdot W(t)-M\cdot \frac{W^2(t)}{h_0}\right)$$

(19)

This differential equation only for the wear and can be analytically solved to:

$$W(t)=h_0\cdot \frac{e^{c_1{h}_{0}M+c_1{h}_0+HMt+Ht}+1}{e^{c_1{h}_{0}M+c_1{h}_0+HMt+Ht}-M}$$

(20)

where c₁ is a constant. As W(0) = 0 leads to:

$$c_1=\frac{\ln (-1/h_0)}{h_0\cdot (M+1)}$$

(21)

and thus to the solution:

$$W(t)=h_0\cdot \frac{e^{Ht(M+1)}-1}{e^{Ht(M+1)}+M}$$

(22)

The contact temperature between the abrasive grain and the workpiece defining H, given by comparison between Equations (18) and (19) is calculated according to [22] as:

$$T_{grind}=3.1\cdot \frac{2\cdot R_w\cdot q_f\cdot \alpha }{\pi \cdot k_T\cdot v_w}\cdot {\left(\frac{v_w\cdot l}{2\cdot \alpha }\right)}^{0.53}$$

(23)

where R_w is the energy partition coefficient, q_f is the heat flux, α is the workpiece thermal diffusivity, k_T is the thermal conductivity of the workpiece, v_w is the workpiece feed rate, and l is the half length of the band source.

A criterion needs to be established for the grain failure. Stresses acting on the abrasive grain are estimated and compared to the critical stress value. The stress in the cutting direction can be estimated as:

$${\sigma }_{cut}=\frac{F_c}{A_{cut}(h(t))}$$

(24)

The stress in the normal direction can be calculated as:

$${\sigma }_N=\frac{F_N}{A_{\perp }}$$

(25)

where F_N is the normal force and $A_{\perp }$ is the cross section of the abrasive grain projected in normal direction. The normal force can be calculated from Equation (11).

Additionally, a shear stress can be calculated as:

$${\tau }_{yz}=\frac{F_c}{b^2}$$

(26)

where F_c is the cutting force and b the width of abrasive grain.

For the calculation of the equivalent stress, the Rankine criterion is used:

$${\sigma }_{result}<{\sigma }_{critical}={300}_{}\mathrm{MPa}$$

(27)

Plotting this resulting stress ${\sigma }_{result}$ qualitatively for different wear factors K and with M = 1 as simplifying assumption, different progressions can be observed as shown in Figure 10.

From Figure 10 and together with the knowledge of the experimentally evaluated average time for an abrasive grain failure and the calculated resulting stress, the wear factor can be evaluated. Wear factor K = 508 × 10⁻⁴ 1/N is estimated as shown in Figure 11.

With the wear factor K, the propagation of wear with time can be calculated according to Equation (22).

4. Results and Discussion

In order to compare and validate the simulation with the experiment, the workpiece surface roughness measurements are done. An indirect measuring method is carried out for all of the roughness measurements. An imprint mass used for dental application is uniformly distributed on the workpiece surface by dispense pistol, as shown in Figure 12. The overall imprint length allows for the maximum measurement length of 80 mm. This imprinting method is time effective and allows for the conservation of the current surface ground for later evaluation without losing the information. The accuracy of this imprinting measuring method is proven in [23].

All of the roughness measurements on the imprints are performed with a tactile roughness measurement device Talysurf from Taylor Hobson, using diamond tip with 2 µm tip radius and cut-off filter 2.5 mm. The measuring direction is along the feed rate direction, perpendicular to the grinding grooves.

For all of the grinding experiments, the following process parameters were used: cutting speed v_c = 47 m/s, feed rate v_w = 120 m/min, and grinding time 6 s. The grinding wheel was in steady state. Pre-dressing, using the self-sharpening effect of the grinding wheel, was performed prior to every experiment.

Figure 13 compares experimental and simulated results between the workpiece surface topography for tilt angle 0.0°. Good agreement between the experimental and simulated roughness values can be achieved. The roughness values Ra and the mean roughness value Rz are summarised in

Table 1. Average roughness Ra and average roughness depth Rz for experiment and simulation.

Tilt Angle	Average Roughness Ra (μm)		Average Roughness Depth Rz (μm)
	Experiment	Simulation	Experiment	Simulation
2.5°	9.8	9.9	61.8	59.4
0.0°	9.5	9.4	61.7	55.7
−1.5°	5.3	6.6	35.7	39.9

. As validation of the model, the comparison of Ra and Rz might be used. For the purpose of this research it is sufficient to verify the prediction of surface properties by Ra and Rz roughness values. The workpiece surface anisotropy is in feed rate direction and in the cutting speed direction. As the workpiece surface roughness, by railway grinding, in the feed rate direction is of interest, Ra and Rz are sufficient.

It can be seen, that for the tilt angle −1.5° in Figure 14, where the grinding wheel is in dual-sided contact with the workpiece, the second part of the grinding wheel ruptures the roughness peaks. The workpiece surface and the corresponding roughness values are lower as for the tilt angle 0.0°. When considering the workpiece surface topology, a crisscross-like pattern can be observed for the tilt angle −1.5°.

The mean roughness Ra reaches Ra = 6.6 µm for the simulation and Ra = 5.3 µm for the experiment. The mean roughness depth Rz reaches Rz = 39.9 µm for the simulation and Rz = 35.7 µm for the experiment.

When comparing the average Ra and Rz roughness values for tilt angles −1.5°, 0.0°, and 2.5° in Table 1, the simulation results at a tilt angle of 2.5° differ by maximum 12.2% for the Ra values and by 14.4% for the Rz values. For the tilt angle 0.0°, the deviation by the Ra values is maximum 5.2% and by the Rz values is 11%. For the double-sided grinding wheel contact, where the tilt angle is −1.5°, the deviation for Ra is 24% and for Rz is 12%. This is caused by the associated approach angle not being equal to zero. The self-sharpening effect of the resin bonded corundum grinding wheel causes grinding wheel adaption on the workpiece geometry. Despite the relatively large difference in the process kinematics for these both tilt angles, one size of the grinding wheel cutting surface is always planar on the ground surface. This condition causes similar roughness values for all different tilt approaches, except the one where the approach angle is zero (only for tilt angle −1.5°).

5. Conclusions

A kinematic process model with the focus on the wear modelling was presented. Time dependent wear behaviour was presented. High feed rates were used for all of the experiments. The dependence of surface roughness on the kinematic situation could be shown. With a dressed grinding wheel, any adjusted tilt angle between ±15° shows the same workpiece roughness. This is because of the self-sharpening of the resin bonded corundum grinding wheel and the adaption to the workpiece geometry. The self-sharpening effect of the corundum grinding wheel shows that only the approach angle 0.0° can improve the surface roughness, where a dual-sided grinding wheel contact is used.

An analytical approach for the wear modelling has been chosen based on previous studies. The wear rate has been modelled as a function of the cutting force, the cutting speed, and the temperature for every abrasive grain. The resulting exponential behaviour of the wear propagation was used for subsequently determining the resulting stress on the abrasive grain, which is compared to some critical stress level to determine the grain failure. With this model, the time delayed failure of a grain could be described. Three wear parameters K, M, and B were introduced based on experimental investigations. The average time for a grain failure was calculated and the wear factor K = 508 × 10⁴ 1/N was estimated.

The simulation results show good agreement with the measured workpiece surface roughness. When comparing the roughness values Ra and Rz, the deviation is by maximum 14.4% for tilt angle 2.5°, 11% for 0.0° and 24% for −1.5°.