Influence of Dimple Height on Turbulent Heat Transfer of Fin Array with Alternate Convex/Concave Dimples
Abstract
:1. Introduction
2. Numerical Method
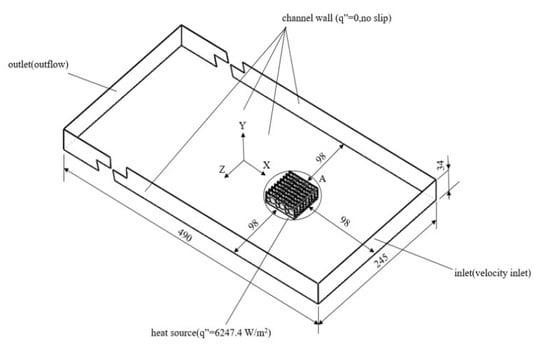
2.1. Geometric Model
2.2. Governing Equations
- for i = 1–3.
- where is the SGS stress tensor [38]:
2.3. Subgrid-Scale (SGS) Model
2.4. Boundary Conditions and Solution Scheme
2.5. Grid and Time-Step Independence Test
- Run the densest model (M3) with three time intervals (T1, T2, T3).
- Check the errors if they are less than 1%. If the errors are less than 1%, choose the middle time interval (T2). Otherwise, change the time interval and run the program again.
- Run the program using the other models (M1, M2) with the chosen time interval (T2).
- Check if the errors are less than 1%. If the errors are less than 1%, choose the model that has middle number of mesh (M2). Otherwise, change the mesh and run the program again.
- Run the program using the M2 model with other time interval (T1, T3).
- Check if the errors of M2 with T1, T2, and T3 are less than 1%. If the errors are less than 1%, the M2 with T1 is the model used for simulating. Otherwise, run steps 1–6 again.
2.6. Verification
3. Results and Discussion
3.1. Influence of Protrusion Height on Flow Field
3.2. Influence of Different Heights of Protrusion on Heat Transfer Performance
3.3. Analysis of Enthalpy Flow Rate (EFR)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Area |
| Drag coefficient () | |
| Specific heat | |
| Smagorinsky constant | |
| D | Height of convex dimple or depth of concave dimple |
| EFR | Enthalpy flow rate (kW) (=) |
| Drag force | |
| h | Specific enthalpy |
| K | Thermal conductivity () |
| L | Length |
| L1 | Length of fin |
| Nu | Nusselt number () |
| p | Pressure () |
| Pr | Prandtl number () |
| Heat flux () | |
| R | Dimple inner radius (mm) |
| Re | Reynolds number () |
| Rate of strain tensor | |
| T | Temperature(K) |
| T | Time(s) |
| Friction velocity () | |
| Dimensionless distance from the wall () | |
| X, Y, Z | Cartesian coordinates (m) |
Greek Symbols
| Filter width | |
| Dynamic viscosity () | |
| Kinematic viscosity () | |
| Thermal diffusivity () | |
| Density () | |
| Stress tensor | |
| Shear stress | |
| SGS stress tensor |
Superscript
| ̶ | Time mean |
| ~ | Spatial filtering indication |
Subscripts
| avg | Averaged area |
| i | Component or grid |
| w | Wall |
| T | Turbulence |
| Ambient |
References
- Zografos, A.I.; Sunderland, J.E. Natural convection from pin fin arrays. Exp. Therm. Fluid Sci. 1990, 3, 440–449. [Google Scholar] [CrossRef]
- Ledezma, G.; Bejan, A. Heat sinks with sloped plate fins in natural and forced convection. Int. J. Heat Mass Transf. 1996, 39, 1773–1783. [Google Scholar] [CrossRef]
- Goshayeshi, H.R.; Fahiminia, M.; Naserian, M.M. Numerical modeling of natural convection on various configuration of rectangular fin arrays on vertical base plates. World Acad. Sci. Eng. Techno. 2011, 73, 91–96. [Google Scholar]
- Chang, S.-W.; Wu, H.W.; Guo, D.-Y.; Shi, J.-J.; Chen, T.-H. Heat transfer enhancement of vertical dimpled fin array in natural convection. Int. J. Heat Mass Transf. 2017, 106, 781–792. [Google Scholar] [CrossRef]
- Afanasyev, V.; Chudnovsky, Y.; Leontiev, A.; Roganov, P. Turbulent flow friction and heat transfer characteristics for spherical cavities on a flat plate. Exp. Therm. Fluid Sci. 1993, 7, 1–8. [Google Scholar] [CrossRef]
- Chang, S.; Chiang, K.; Yang, T.; Huang, C. Heat transfer and pressure drop in dimpled fin channels. Exp. Therm. Fluid Sci. 2008, 33, 23–40. [Google Scholar] [CrossRef]
- Ligrani, P.; Mahmood, G.I.; Harrison, J.; Clayton, C.; Nelson, D. Flow structure and local Nusselt number variations in a channel with dimples and protrusions on opposite walls. Int. J. Heat Mass Transf. 2001, 44, 4413–4425. [Google Scholar] [CrossRef]
- Fazli, M.; Raisee, M. Computation of flow and heat transfer through channels with periodic dimple/protrusion walls using low-Reynolds number turbulence models. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 1178–1207. [Google Scholar] [CrossRef]
- Luo, L.; Du, W.; Wang, S.; Wu, W.; Zhang, X. Multi-objective optimization of the dimple/protrusion channel with pin fins for heat transfer enhancement. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 790–813. [Google Scholar] [CrossRef]
- Sobhani, E.; Ghaffari, M.; Maghrebi, M.J. Numerical investigation of dimple effects on darrieus vertical axis wind turbine. Energy 2017, 133, 231–241. [Google Scholar] [CrossRef]
- Jung, H.-Y.; Kim, K.-Y. Thermal-hydraulic performance of a multiple jet cooling module with a concave dimple array in a helium-cooled divertor. Fusion Eng. Des. 2017, 114, 102–112. [Google Scholar] [CrossRef]
- Kim, S.-M.; Jo, J.-H.; Lee, Y.-E.; Yoo, Y.-S. Comparative study of shell and helically-coiled tube heat exchangers with various dimple arrangements in condensers for odor control in a Pyrolysis System. Energies 2016, 9, 1027. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.; Wang, G.; Ding, Y.; Yang, J.; Zhai, H. Investigation of the effect of dimple bionic nonsmooth surface on tire antihydroplaning. Appl. Bionics Biomech. 2015, 2015, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Xie, G.; Liu, J.; Ligrani, P.M.; Zhang, W. Numerical analysis of flow structure and heat transfer characteristics in square channels with different internal-protruded dimple geometrics. Int. J. Heat Mass Transf. 2013, 67, 81–97. [Google Scholar] [CrossRef]
- Rao, Y.; Wan, C.; Zang, S. An experimental and numerical study of flow and heat transfer in channels with pin fin-dimple combined arrays of different configurations. J. Heat Transf. 2012, 134, 121901. [Google Scholar] [CrossRef]
- Sethi, M. An experimental and numerical study of flow and heat transfer in channels with Pin Fin-dimple combined arrays of different configurations. J. Renew. Sustain. Energy 2012, 4, 023112. [Google Scholar] [CrossRef]
- Lan, J.; Xie, Y.; Zhang, D. Effect of leading edge boundary layer thickness on dimple flow structure and separation control. J. Mech. Sci. Technol. 2011, 25, 3243–3251. [Google Scholar] [CrossRef]
- Dees, J.E.; Bogard, D.G.; Bunker, R.S. Heat transfer augmentation downstream of rows of various dimple geometries on the suction side of a gas turbine airfoil. J. Turbomach. 2010, 132, 031010. [Google Scholar] [CrossRef]
- Mitsudharmadi, H.; Tay, C.M.J.; Tsai, H.M. Effect of rounded edged dimple arrays on the boundary layer development. J. Vis. 2009, 12, 17–25. [Google Scholar] [CrossRef]
- Won, S.Y.; Ligrani, P.M. Flow characteristics along and above dimpled surfaces with three different dimple depths within a channel. J. Mech. Sci. Technol. 2007, 21, 1901–1909. [Google Scholar] [CrossRef]
- Rao, Y.; Wan, C.; Xu, Y. An experimental study of pressure loss and heat transfer in the pin fin-dimple channels with various dimple depths. Int. J. Heat Mass Transf. 2012, 55, 6723–6733. [Google Scholar] [CrossRef]
- Li, M.; Chen, X.; Ruan, X. Investigation of flow structure and heat transfer enhancement in rectangular channels with dimples and protrusions using large eddy simulation. Int. J. Therm. Sci. 2020, 149, 106207. [Google Scholar] [CrossRef]
- Elyyan, M.A.; Tafti, D.K. Large eddy simulation investigation of flow and heat transfer in a channel with dimples and protrusions. J. Turbomach. 2008, 130, 041016. [Google Scholar] [CrossRef]
- Sato, N.; Inagaki, M.; Kaneda, K.; Horinouchi, N.; Ota, A. Numerical investigation of the effect of Prandtl number on heat transfer in a dimpled-channel flow. Int. J. Heat Fluid Flow 2017, 68, 139–150. [Google Scholar] [CrossRef]
- Torregrosa, A.; Gil, A.; Quintero, P.; Ammirati, A.; Denayer, H.; Desmet, W. Prediction of flow induced vibration of a flat plate located after a bluff wall mounted obstacle. J. Wind. Eng. Ind. Aerodyn. 2019, 190, 23–39. [Google Scholar] [CrossRef]
- Le Hocine, A.E.B.; Lacey, R.W.J.; Poncet, S. Turbulent flow over a D-section bluff body: A numerical benchmark. Environ. Fluid Mech. 2018, 19, 435–456. [Google Scholar] [CrossRef]
- Alam, J.; Fitzpatrick, L.P. Large eddy simulation of flow through a periodic array of urban-like obstacles using a canopy stress method. Comput. Fluids 2018, 171, 65–78. [Google Scholar] [CrossRef]
- Lu, H.; Zhao, W.; Zhang, H.; Wang, B.; Wang, X.-L. Three-dimensional turbulent flow over cube-obstacles. Chin. Phys. B 2017, 26, 14703. [Google Scholar] [CrossRef]
- Saeedi, M.; Wang, B.-C. Large-eddy simulation of turbulent flow around a finite-height wall-mounted square cylinder within a thin boundary layer. Flow, Turbul. Combust. 2016, 97, 513–538. [Google Scholar] [CrossRef]
- Hao, Z.; Gorlé, C. Large eddy simulations of forced heat convection in a pin-fin array with a priori examination of an eddy-viscosity turbulence model. Int. J. Heat Fluid Flow 2019, 77, 73–83. [Google Scholar] [CrossRef]
- Toubiana, E.; Russeil, S.; Bougeard, D.; François, N. Large Eddy simulation and Reynolds-averaged Navier–Stokes modeling of flow in staggered plate arrays: Comparison at various flow regimes. Appl. Therm. Eng. 2015, 89, 405–420. [Google Scholar] [CrossRef]
- Paniagua, L.; Lehmkuhl, O.; Oliet, C.; Pérez-Segarra, C.D. Large eddy simulations (LES) on the flow and heat transfer in a wall-bounded pin matrix. Numer. Heat Transf. Part B Fundam. 2014, 65, 103–128. [Google Scholar] [CrossRef]
- Chen, J.G.; Zhou, Y.; Zhou, T.M.; Antonia, R.A. Three-dimensional vorticity, momentum and heat transport in a turbulent cylinder wake. J. Fluid Mech. 2016, 809, 135–167. [Google Scholar] [CrossRef]
- Yang, K.-S.; Ferziger, J.H.; Ferzigert, J.H. Large-eddy simulation of turbulent obstacle flow using a dynamic subgrid-scale model. AIAA J. 1993, 31, 1406–1413. [Google Scholar] [CrossRef]
- Franke, J.; Frank, W. Large eddy simulation of the flow past a circular cylinder at ReD= 3900. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1191–1206. [Google Scholar] [CrossRef]
- Ma, X.; Karamanos, G.-S.; Karniadakis, G. Dynamics and low-dimensionality of a turbulent near wake. J. Fluid Mech. 2000, 410, 29–65. [Google Scholar] [CrossRef] [Green Version]
- Ong, L.; Wallace, J. The velocity field of the turbulent very near wake of a circular cylinder. Exp. Fluids 1996, 20, 441–453. [Google Scholar] [CrossRef]
- Johnson, R.W. The Handbook of Fluid Dynamics; CRC Press: New York, NY, USA, 1998; pp. 1487–1488. [Google Scholar]
- Smagorinsky, J. General circulation experiments with the primitive equations. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Jayatilleke, C.L.V. The influence of Prandtl number and surface roughness on the resistance of the laminar sublayer to momentum and heat transfer. Prog. Heat Mass Transf. 1969, 1, 193–329. [Google Scholar]
- Lockett, J.F. Heat Transfer from Toughened Surfaces Using Laser Interferometers. Ph.D. Thesis, Department of Mechanical Engineering, The City University, London, UK, 1987. [Google Scholar]
- Tsui, Y.-Y. A study of upstream-weighted high-order differencing for approximation to flow convection. Int. J. Numer. Methods Fluids 1991, 13, 167–199. [Google Scholar] [CrossRef]
- Deng, G.B.; Piquet, J.; Queutey, P.; Visonneau, M. A new fully coupled solution of the Navier-Stokes equations. Int. J. Numer. Methods Fluids 1994, 19, 605–639. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Informa UK Limited: London, UK, 2018. [Google Scholar]
- Ahn, J.; Lee, J.S. Large eddy simulation of flow and heat transfer in a channel with a detached rib array. Int. J. Heat Mass Transf. 2010, 53, 445–452. [Google Scholar] [CrossRef]












| Model | Mesh Symbol | Mesh | Time Step Symbol | Time Step (Sec) |
|---|---|---|---|---|
| F0 | M1 | 2,201,819 | T1 | 0.2 |
| M2 | 2,969,578 | T2 | 0.3 | |
| M3 | 3,365,018 | T3 | 0.4 | |
| F1 | M1 | 2,054,326 | T1 | 0.2 |
| M2 | 2,986,580 | T2 | 0.3 | |
| M3 | 3,280,354 | T3 | 0.4 | |
| F2 | M1 | 2,029,788 | T1 | 0.2 |
| M2 | 2,717,655 | T2 | 0.3 | |
| M3 | 3,258,359 | T3 | 0.4 | |
| F3 | M1 | 2,086,485 | T1 | 0.2 |
| M2 | 2,820,624 | T2 | 0.3 | |
| M3 | 3,310,515 | T3 | 0.4 |
| F0 | F1 | ||
| Symbol | Symbol | ||
| F0M3T1 | 0 | F1M3T1 | 0 |
| F0M3T2 | 0.0194% | F1M3T2 | 0.0226% |
| F0M3T3 | 0.0316% | F1M3T3 | 0.0343% |
| F0M1T2 | 0.0029% | F1M1T2 | 0.0239% |
| F0M2T2 | 0.0199% | F1M2T2 | 0.2365% |
| F0M2T1 | 0.0666% | F1M2T1 | 0.0133% |
| F0M2T3 | 0.0316% | F1M2T3 | 0.0359% |
| F2 | F3 | ||
| Symbol | Symbol | ||
| F2M3T1 | 0 | F3M3T1 | 0 |
| F2M3T2 | 0.0259% | F3M3T2 | 0.0233% |
| F2M3T3 | 0.0389% | F3M3T3 | 0.0346% |
| F2M1T2 | 0.273% | F3M1T2 | 0.0246% |
| F2M2T2 | 0.0752% | F3M2T2 | 0.0066% |
| F2M2T1 | 0.04364% | F3M2T1 | 0.0663% |
| F2M2T3 | 0.0912% | F3M2T3 | 0.0353% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.-W.; Chen, T.-H.; Kelana, N.-P.; Huang, D.-A. Influence of Dimple Height on Turbulent Heat Transfer of Fin Array with Alternate Convex/Concave Dimples. Inventions 2020, 5, 33. https://doi.org/10.3390/inventions5030033
Wu H-W, Chen T-H, Kelana N-P, Huang D-A. Influence of Dimple Height on Turbulent Heat Transfer of Fin Array with Alternate Convex/Concave Dimples. Inventions. 2020; 5(3):33. https://doi.org/10.3390/inventions5030033
Chicago/Turabian StyleWu, Horng-Wen, Tang-Hong Chen, Nugroho-Putra Kelana, and De-An Huang. 2020. "Influence of Dimple Height on Turbulent Heat Transfer of Fin Array with Alternate Convex/Concave Dimples" Inventions 5, no. 3: 33. https://doi.org/10.3390/inventions5030033
APA StyleWu, H. -W., Chen, T. -H., Kelana, N. -P., & Huang, D. -A. (2020). Influence of Dimple Height on Turbulent Heat Transfer of Fin Array with Alternate Convex/Concave Dimples. Inventions, 5(3), 33. https://doi.org/10.3390/inventions5030033