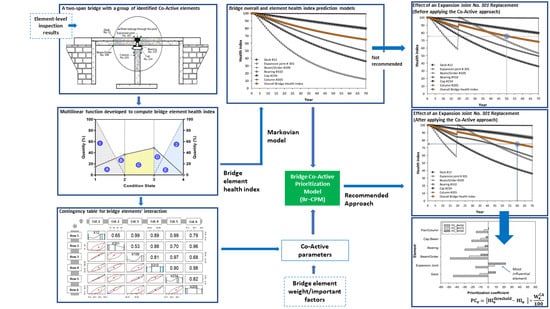
Co-Active Prioritization by Means of Contingency Tables for Analyzing Element-level Bridge Inspection Results and Optimizing Returns
Abstract
:1. Introduction
1.1. General Background on Bridge Elements
1.2. Motivation
1.3. Research Goals
- Can one define inter-dependent relationships among bridge elements’ health indices?
- How should one optimize a return on investment (ROI) in terms of bridge service life extension? That is, how should one quantify the effects of inter-element relationships as a function of time and evaluate bridge long-term performance?
- Do inter-element relationships affect importance weighting factors and help prioritize actions (preventive maintenance, rehabilitation, or replacement) on bridge elements?
1.4. Research Scope
- In Part 1, inter-element relationships are defined and described as a function of time (time-dependent Co-Active coefficient).
- In Part 2, collaboration factors are computed to determine the Prioritization Coefficient (PC), by applying Co-Active coefficients from a contingency table.
- In part 3, bridge elements and overall health indices are assessed.
1.5. Significance
2. Literature Review
3. Methodology
3.1. Development of Contingency Tables
3.1.1. Identify Groups by Bridge Types
- Steel open girder/beam bridge (SO107): This group consisted of bridges with steel open girder (I section) as the means of supporting the overlying reinforced concrete deck, and in transmitting loads from the reinforced concrete deck into the underlying substructure. There were 598 bridges in this group. The last three numbers, ‘107’, in ‘SO107’, is an element identification number for steel open girder/beam bridge element. The first two letters, ‘SO’, means steel open, added to emphasize this group and make it unique in representation.
- Prestressed concrete open girder/beam bridge (PC109): In this group, each bridge contained prestressed concrete as the open girder/beam element’s material. The open girder/beam element in this bridge group performed similar functions as described in the group ‘SO107’, steel open girder/beam bridge. There were 1439 bridges in this group. Figure 2 shows a typical in-service prestressed concrete girder/beam bridge, which is the most common type in Georgia.
- Reinforced concrete open girder/beam with pile foundation bridge (RC110): Unlike the other two groups, bridges in this group contained reinforced concrete as a construction material for the open girder/beam element. In addition, each bridge contained a pile foundation. There were 1098 bridges in this group.
3.1.2. Create 12 Age Bins for Bridges in Each Group
3.1.3. Compute Health Indexes for Elements in Each Age Bin
3.1.4. Develop Deterioration Prediction for Each Element
3.1.5. Develop Contingency Tables and Determine Element Co-Active Coefficients
3.2. Computation of Element Collobaration Factors
3.2.1. Existing Element Weight Factors
3.2.2. Collaboration Factors
- = Collaboration factor,
- = Weight factor [10] given to element, ‘e’,
- = Co-Active correlation coefficient between two elements’ HIs (from Equation (2)),
- = the number of Co-Active elements.
3.3. Bridge Health Index Assessment
4. Analytical Investigation of Co-Active Elements in Three Bridge Groups
4.1. Contingency Table for Co-Active Coefficients
4.2. Collaboration Factors
4.3. Effect of Co-Active Elements on the Bridge Health Index
4.3.1. Results Obtained without Co-Active Model
4.3.2. Results Obtained with Co-Active Model
- The year in which a Co-Active element was maintained, rehabilitated, or replaced (MRR).
- The condition of a Co-Active element (i.e., an element HI) before MRR and the type of MRR action. The more the performance gap (i.e., the difference between an element’s HI before and after MRR), the more influential the element’s MRR was on the HI predictions.
- The inter-dependencies among the Co-Active elements. The elements’ inter-dependency was a function of their Co-Active coefficients. The higher the value of an element Co-Active coefficient, the more dependent the element was.
5. Analysis and Interpretation of Results and Implementation
5.1. Prioritization for Bridge Maintenance
- = Prioritization coefficient,
- = Health index,
- = Threshold health index,
- = Collaboration factor.
5.2. Discussion of Results
6. Conclusions
7. Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- AASHTO. Manual for Bridge Element Inspection, 2nd ed.; American Association of State Highway and Transportation Officials: Washington, DC, USA, 2019. [Google Scholar]
- Phillips, P.S.T. Predicting Costs for Bridge Replacement Projects; The University of North Carolina at Charlotte: Charlotte, NC, USA, 2017. [Google Scholar]
- Puls, E.; Hueste, M.B.D.; Hurlebaus, S.; Damnjanovic, I. Prioritization of a bridge inventory for historic preservation: A case study for Tarrant County, Texas. Publ. Works Manag. Pol. 2018, 23, 205–220. [Google Scholar] [CrossRef]
- Sabatino, S.; Frangopol, D.M. Decision support system for optimum lifetime sustainability-based maintenance planning of highway bridges. In Proceedings of the International Conference on Sustainable Infrastructure, New York, NY, USA, 26–28 October 2017. [Google Scholar]
- Inkoom, S.; Sobanjo, J. Availability function as bridge element’s importance weight in computing overall bridge health index. Struct. Infrastruct. Eng. 2018, 14, 1–13. [Google Scholar] [CrossRef]
- Jiang, X.; Rens, K.L. Bridge health index for the city and county of Denver, Colorado. I: Current methodology. J. Perform. Constr. Facil. 2010, 24, 580–587. [Google Scholar] [CrossRef]
- Jiang, X.; Rens, K.L. Bridge health index for the city and county of Denver, Colorado. II: Denver bridge health index. J. Perform. Constr. Facil. 2010, 24, 588–596. [Google Scholar] [CrossRef]
- Inkoom, S.; Sobanjo, J.O.; Thompson, P.D.; Kerr, R.; Twumasi-Boakye, R. Bridge health index: study of element condition states and importance weights. Transport. Res. Rec. 2017, 2612, 67–75. [Google Scholar] [CrossRef]
- Adhikari, R.S.; Moselhi, O.; Bagchi, A. A study of image-based element condition index for bridge inspection. In Proceedings of the International Symposium on Automation and Robotics in Construction, Montréal, QC, Canada, 11–15 August 2013. [Google Scholar]
- Sobanjo, J.O.; Thompson, P.D. Implementation of the 2013 AASHTO manual for bridge element inspection; Report No. BDV30-977-07; Florida State University: Tallahassee, FL, USA, 2016; p. 179. [Google Scholar]
- Anderson, I.; Rizzo, D.M.; Huston, D.R.; Dewoolkar, M.M. Analysis of bridge and stream conditions of over 300 Vermont bridges damaged in Tropical Storm Irene. Struct. Infrastruct. Eng. 2017, 13, 1437–1450. [Google Scholar] [CrossRef]
- Weidner, J.; Prader, J.; Dubbs, N.; Moon, F.; Aktan, A.E.; Taylor, J.; Skeens, C. Extending the life of aged, reinforced concrete arch bridges through load testing and monitoring. ACI Spec. Publ. 2018, 323, 12.11–12.16. [Google Scholar]
- Chase, S.B.; Adu-Gyamfi, Y.; Aktan, A.; Minaie, E. Synthesis of National and International Methodologies Used for Bridge Health Indices; FHWA-HRT-15-081; Federal Highway Administration: McLean, VA, USA, 2016.
- Lake, N.; Seskis, J. Bridge Management Using Performance Models; AP-T258/13; Austroads: New South Wales, Australia, 2013. [Google Scholar]
- Jonnalagadda, S.; Ross, B.E.; Khademi, A. A modelling approach for evaluating the effects of design variables on bridge condition ratings. J. Struct. Integrity Maint. 2016, 1, 167–176. [Google Scholar] [CrossRef]
- Fereshtehnejad, E.; Hur, J.; Shafieezadeh, A.; Brokaw, M.; Backs, J.; Noll, B.; Waheed, A. A bridge performance index with objective incorporation of safety risks. In Proceedings of the Transportation Research Board 97th Annual Meeting, Washington, DC, USA, 7–11 January 2018. [Google Scholar]
- Jeong, Y.; Kim, W.; Lee, I.; Lee, J. Bridge inspection practices and bridge management programs in China, Japan, Korea, and US. J. Struct. Integrity Maint. 2018, 3, 126–135. [Google Scholar] [CrossRef]
- Verhoeven, J.; Flintsch, G. Generalized framework for developing a corridor-level infrastructure health index. Transport. Res. Rec. 2011, 20–27. [Google Scholar] [CrossRef]
- Matteo, A.; Milton, J.; Springer, T. Using Asset Valuation as a Basis for Bridge Maintenance and Replacement Decisions. Available online: http://onlinepubs.trb.org/Onlinepubs/webinars/160411.pdf (accessed on 18 September 2017).
- Matteo, A. State of Good Reapir (SGR) Program: Bridge Prioritization Formula. Available online: http://www.virginiadot.org/business/resources/local_assistance/StateofGoodRepair/SGR_Locally_Owned_Bridges_Prioritization_Process_-_Adam_Matteo_PowerPoint.pdf (accessed on 15 January 2020).
- Shepard, R.W.; Johnson, M.B. California Bridge Health Index: A Diagnostic Tool to Maximize Bridge Longevity, Investment; Transportation Research Board: Washington, DC, USA, 2001; pp. 6–11. [Google Scholar]
- Spyrakos, C.; Loannidis, G. Seismic behavior of a post-tensioned integral bridge including soil–structure interaction (SSI). Soil Dyn. Earthq. Eng. 2003, 23, 53–63. [Google Scholar] [CrossRef]
- Mehrabi, A.B. In-service evaluation of cable-stayed bridges, overview of available methods and findings. J. Bridge Eng. 2006, 11, 716–724. [Google Scholar] [CrossRef]
- Enright, M.P.; Frangopol, D.M. Survey and evaluation of damaged concrete bridges. J. Bridge Eng. 2000, 5, 31–38. [Google Scholar] [CrossRef]
- Yianni, P.C.; Rama, D.; Neves, L.C.; Andrews, J.D.; Castlo, D. A Petri-Net-based modelling approach to railway bridge asset management. Struct. Infrastruct. Eng. 2017, 13, 287–297. [Google Scholar] [CrossRef] [Green Version]
- Yarnold, M.; Weidner, J. Monitoring of a bascule bridge during construction. In Proceedings of the Transportation Research Board 95th Annual Meeting, Washington, DC, USA, 10–14 January 2016. [Google Scholar]
- De Risi, R.; Di Sarno, L.; Paolacci, F. Probabilistic seismic performance assessment of an existing RC bridge with portal-frame piers designed for gravity loads only. Eng. Struct. 2017, 145, 348–367. [Google Scholar] [CrossRef]
- Thompson, P.D.; Bye, P.; Western, J.; Valeo, M. Risk assessment for bridge management systems. In Proceedings of the 9th International Conference on Bridge Maintenance, Safety and Management, Melbourne, Australia, 9–13 July 2018. [Google Scholar]
- Thomas, O.; Sobanjo, J. Semi-Markov models for the deterioration of bridge elements. J. Infrastruct. Syst. 2016, 22, 04016010. [Google Scholar] [CrossRef]
- Thomas, O.; Sobanjo, J. Comparison of Markov chain and semi-Markov models for crack deterioration on flexible pavements. J. Infrastruct. Syst. 2012, 19, 186–195. [Google Scholar] [CrossRef]
- Salim, W.S.W.; Liew, M.S.; Shafie, A.f. Qualitative fault tree and event tree model of bridge defect for reinforced concrete highway bridge. In Proceedings of the International Civil and Infrastructure Engineering Conference Kota Kinabalu, Sabah, Malaysia, 28 September–1 October 2014; pp. 639–650. [Google Scholar]
- Patidar, V.; Labi, S.; Sinha, K.; Thompson, P. Multi-Objective Optimization for Bridge Management Systems; Report No. 590; Transportation Research Board: Washington, DC, USA, 2007. [Google Scholar]
- Hearn, G. Element-Level Performance Measures for Bridge Preservation; Transportation Research Board: Washington, DC, USA, 2015; pp. 10–17. [Google Scholar]
- Kosgodagan-Dalla Torre, A.; Yeung, T.G.; Morales-Nápoles, O.; Castanier, B.; Maljaars, J.; Courage, W. A two-dimension dynamic Bayesian network for large-scale degradation modeling with an application to a bridges network. Comput-Aided Civ. Infrastruct. Eng. 2017, 32, 641–656. [Google Scholar] [CrossRef] [Green Version]
- Dori, G.; Wild, M.; Borrmann, A.; Fischer, O. A system model based approach for lifecycle monitoring of bridges. In Proceedings of the 3rd International Conference on Soft Computing Technology in Civil, Structural and Environmental Engineering, Cagliari, Sardinia, Italy, 3–6 September 2013. [Google Scholar]
- LeBeau, K.; Wadia-Fascetti, S. A fault tree model of bridge deterioration. In Proceedings of the 8th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliability, Notre Dame, IN, USA, 24–26 July 2000. [Google Scholar]
- Sianipar, P.R.; Adams, T.M. Fault-tree model of bridge element deterioration due to interaction. J. Infrastruct. Syst. 1997, 3, 103–110. [Google Scholar] [CrossRef]
- NCHRP. Performance measures and targets for transportation asset management; 551; Transportation Research Board: Washington, DC, USA, 2006. [Google Scholar]
- Bu, G.; Lee, J.; Guan, H.; Blumenstein, M.; Loo, Y.-C. Improving reliability of Markov-based bridge deterioration model using Artificial Neural Network. In Proceedings of the IABSE-IASS Symposium - Taller, Longer, Lighter, London, UK, 20–23 September 2011. [Google Scholar]
- Chang, M.; Maguire, M. Developing Deterioration Models for Wyoming Bridges; FHWA-WY-16/09F; Utah State University: Logan, UT, USA, 2016. [Google Scholar]
- Chorzepa, M.G.; Durham, S.; Kim, S.K.; Oyegbile, O.B. Bridge Asset Valuation Utilizing Condition States Obtained from Element-Based Inspection Inventories and Depreciation Models over the Life Cycle of the Assets; Report No. FHWA-GA-19-1728; University of Georgia: Atlanta, GA, USA, 2019; p. 101. [Google Scholar]
- Embrechts, P.; McNeil, A.J.; Straumann, D. Correlation and dependence in risk management: properties and pitfalls. In Risk Management: Value at Risk and Beyond; Cambridge University Press: Cambridge, UK, 2002; Volume 1, pp. 176–223. [Google Scholar]
- Agrawal, A.K.; Kawaguchi, A.; Chen, Z. Deterioration rates of typical bridge elements in New York. J. Bridge Eng. 2010, 15, 419–429. [Google Scholar] [CrossRef]
- FHWA. Bridge Preservation Guide: Maintaining a Resilient Infrastructure to Preserve Mobility; FHWA-HIF-18-022; Federal Highway Administration: Washington, DC, USA, 2018.
















| STRUCNUM | EN | TOTAL QTY (m2) | CS1 (m2) | CS2 (m2) | CS3 (m2) | CS4 (m2) |
|---|---|---|---|---|---|---|
| 20700220 | 12 | 310 | 0 | 264 | 46 | 0 |
| 19950080 | 12 | 67 | 67 | 0 | 0 | 0 |
| 28500340 | 12 | 1526 | 0 | 0 | 1526 | 0 |
| 19950740 | 12 | 42 | 0 | 42 | 0 | 0 |
| 26300160 | 12 | 499 | 487 | 11 | 0 | 0 |
| 6300860 | 12 | 191 | 0 | 0 | 191 | 0 |
| 19950490 | 12 | 36 | 0 | 36 | 0 | 0 |
| 19900470 | 12 | 328 | 0 | 317 | 10 | 0 |
| 20700210 | 12 | 310 | 0 | 294 | 16 | 0 |
| 25550440 | 12 | 85 | 0 | 85 | 0 | 0 |
| 19950520 | 12 | 279 | 0 | 0 | 279 | 0 |
| 19950680 | 12 | 80 | 0 | 80 | 0 | 0 |
| 17100110 | 12 | 232 | 0 | 231 | 0 | 0 |
| 19950620 | 12 | 72 | 72 | 0 | 0 | 0 |
| 20700140 | 12 | 226 | 0 | 213 | 13 | 0 |
| Row A—Quantity Sum | 4283(a) | 626(b) | 1573(c) | 2081(d) | 0(e) | |
| *Row B—% Quantity | 100 | 14.62(f) | 36.73(g) | 48.59(h) | 0(i) | |
| Age-bin | % Quantities in each condition state | ||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| (Good) | (Fair) | (Poor) | (Severe) | ||
| 2020 | 99.52 | 0.48 | 0 | 0 | |
| 2010 | 90.39 | 8.10 | 1.51 | 0 | |
| 2000 | 76.17 | 22.27 | 1.56 | 0 | |
| 1990 | 75.41 | 21.26 | 3.33 | 0 | |
| 1980 | 60.19 | 39.70 | 0.11 | 0 | |
| 1970 | 25.61 | 62.58 | 11.81 | 0 | |
| 1960 | 18.57 | 70.63 | 10.8 | 0 | |
| 1950 | 24.77 | 54.96 | 20.28 | 0 | |
| ** 1940 | 14.62 | 36.73 | 48.59 | 0 | (See “Row B”, in Table 1) |
| 1930 | 0 | 0 | 0 | 0 | |
| 1920 | 0 | 0 | 0 | 0 | |
| 1910 | 0 | 0 | 0 | 0 | |
| (a) Age-bin | Aggregated Percentage Quantity | HI12 | ||||
|---|---|---|---|---|---|---|
| (Area ‘A’) | (Area ‘B’) | (Area ‘C’) | (Area ‘D’) | (Area ‘E’) | ||
| 2020 | 49.90 | 0.10 | 0.20 | 0 | 0 | 99.80 |
| 2010 | 47.40 | 1.90 | 4.80 | 0 | 0.70 | 96.20 |
| 2000 | 43.80 | 5.40 | 11.90 | 0 | 0.80 | 91.40 |
| 1990 | 43.40 | 4.90 | 12.30 | 0.10 | 1.60 | 90.50 |
| 1980 | 40.00 | 9.90 | 19.90 | 0 | 0.10 | 86.40 |
| 1970 | 29.80 | 14.30 | 37.20 | 0.60 | 5.30 | 70.50 |
| 1960 | 28.20 | 16.40 | 40.70 | 0.50 | 4.90 | 68.50 |
| 1950 | 28.30 | 11.60 | 37.60 | 1.70 | 8.40 | 67.00 |
| 1940 | 20.20 | 5.50 | 42.70 | 8 | 16.40 | 51.20 |
| 1930 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1920 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1910 | 0 | 0 | 0 | 0 | 0 | 0 |
| (b) Weighing factors [8] | 2.0 | 0.24 | 0.20 | 0.12 | 0.0 | |
| Age-bin | Deck | Expansion Joint | Beam/Girder | Bearing | Cap Beam | Pier/Column |
|---|---|---|---|---|---|---|
| 2020 | 95.26 | 83.58 | 97.65 | 88.41 | 99.92 | 100.00 |
| 2010 | 92.30 | 74.34 | 98.92 | 95.95 | 93.28 | 97.68 |
| 2000 | 90.15 | 75.05 | 98.97 | 87.42 | 95.67 | 96.20 |
| 1990 | 83.73 | 53.36 | 98.02 | 93.99 | 95.79 | 95.34 |
| 1980 | 89.15 | 67.42 | 97.87 | 89.25 | 96.87 | 94.82 |
| 1970 | 77.76 | 67.50 | 95.03 | 84.22 | 94.57 | 94.60 |
| 1960 | 73.51 | 60.03 | 91.82 | 78.77 | 92.86 | 89.23 |
| 1950 | 63.32 | 34.68 | 82.26 | 66.45 | 93.14 | 81.31 |
| 1940 | 61.28 | 59.72 | 80.71 | 69.66 | 74.41 | 89.06 |
| (a) On the element below | The Effect of the Following Element’s Condition Change | |||||
|---|---|---|---|---|---|---|
| Deck | Expansion Joint | Beam/Girder | Bearing | Cap Beam | Pier/Column | |
| Deck | 1.00 | |||||
| Expansion Joint | 0.78 | 1.00 | ||||
| Beam/Girder | 0.94 | 0.68 | 1.00 | |||
| Bearing [a] = | ‘A’ = 0.90 | 0.64 | 0.95 | 1.00 | ||
| Cap Beam | 0.72 | 0.28 | 0.75 | 0.60 | 1.00 | |
| Pier/Column | 0.90 | 0.89 | 0.86 | 0.88 | 0.44 | 1.00 |
| (b) Aggregated Co-Active coefficient | ||||||
| 5.24 (Rank 1) | 3.49 (Rank 2) | 3.56 (Rank 3) | 2.48 | 1.44 | 1.00 | |
| (c) Importance weight [10] factor, [c]= | ||||||
| 25.00 (Rank 3) | 12.00 | 49.00 (Rank 1) | 12.00 | 13.00 | 40.00 (Rank 2) | |
| (d) Collaboration factor = [c][a] | ||||||
| 136.58 (Rank 1) | 92.24 (Rank 3) | 104.55 (Rank 2) | 55.00 | 30.60 | 40.00 | |
| On the element below | The Effect of the Following Element’s Condition Change | |||||
|---|---|---|---|---|---|---|
| Deck | Expansion Joint | Beam/Girder | Bearing | Cap Beam | Pier/Column | |
| Deck | 1.00 | |||||
| Expansion Joint | 0.65 | 1.00 | ||||
| Beam/Girder | 0.99 | 0.53 | 1.00 | |||
| Bearing | 0.89 | 0.88 | 0.81 | 1.00 | ||
| Cap Beam | 0.99 | 0.70 | 0.97 | 0.90 | 1.00 | |
| Pier/Column | 0.79 | ‘B’ = 0.96 | 0.68 | 0.98 | 0.82 | 1.00 |
| (b) Aggregated Co-Active coefficient | ||||||
| 5.31 (Rank 1) | 4.07 (Rank 2) | 3.46 (Rank 3) | 2.88 | 1.82 | 1.00 | |
| (c) Importance weight [10] factor | ||||||
| 25.00 (Rank 3) | 12.00 | 46.00 (Rank 1) | 13.00 | 13.00 | 40.00 (Rank 2) | |
| (d) Collaboration factor | ||||||
| 134.38 (Rank 1) | 95.32 (Rank 3) | 96.34 (Rank 2) | 63.90 | 45.80 | 40.00 | |
| (a) On the Element Below | The Effect of the Following Element’s Condition Change | ||||
|---|---|---|---|---|---|
| Deck | Expansion Joint | Beam/Girder | Cap Beam | Pile | |
| Deck | 1.00 | ||||
| Expansion Joint | 0.84 | 1.00 | |||
| Beam/Girder | 0.85 | 0.62 | 1.00 | ||
| Cap Beam | 0.94 | 0.97 | 0.80 | 1.00 | |
| Pile | 0.63 | 0.95 | 0.38 | 0.83 | 1.00 |
| (b) Aggregated Co-Active coefficient | |||||
| 4.26 (Rank 1) | 3.54 (Rank 2) | 2.18 (Rank 3) | 1.83 | 1.00 | |
| (c) Importance weight [10] factor | |||||
| 25.00 (Rank 2) | 12.00 | 33.00 (Rank 1) | 13.00 | 17.00 (Rank 3) | |
| (d) Collaboration factor | |||||
| 86.06 (Rank 1) | 61.22 (Rank 2) | 49.86 (Rank 3) | 27.11 | 17.00 | |
| Negative (-) PC | Positive (+) PC | ||
|---|---|---|---|
| Coefficient | Description | Coefficient | Description |
| PC ≥ 100 | Very Low Priority | PC ≥ 100 | Very High Priority |
| 90 ≤ PC < 100 | Low Priority | 90 ≤ PC < 100 | High Priority |
| 80 ≤ PC < 90 | 80 ≤ PC < 90 | ||
| 70 ≤ PC < 80 | 70 ≤ PC < 80 | ||
| 60 ≤ PC < 70 | 60 ≤ PC < 70 | ||
| 50 ≤ PC < 60 | Medium Priority | 50 ≤ PC < 60 | Medium Priority |
| 40 ≤ PC < 50 | 40 ≤ PC < 50 | ||
| 30 ≤ PC < 40 | High Priority | 30 ≤ PC < 40 | Low Priority |
| 20 ≤ PC < 30 | 20 ≤ PC < 30 | ||
| 10 ≤ PC < 20 | 10 ≤ PC < 20 | ||
| 0 ≤ PC < 10 | Very High Priority | 0 ≤ PC < 10 | Very Low Priority |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oyegbile, O.B.; Chorzepa, M.G. Co-Active Prioritization by Means of Contingency Tables for Analyzing Element-level Bridge Inspection Results and Optimizing Returns. Infrastructures 2020, 5, 13. https://doi.org/10.3390/infrastructures5020013
Oyegbile OB, Chorzepa MG. Co-Active Prioritization by Means of Contingency Tables for Analyzing Element-level Bridge Inspection Results and Optimizing Returns. Infrastructures. 2020; 5(2):13. https://doi.org/10.3390/infrastructures5020013
Chicago/Turabian StyleOyegbile, O. Brian, and Mi G. Chorzepa. 2020. "Co-Active Prioritization by Means of Contingency Tables for Analyzing Element-level Bridge Inspection Results and Optimizing Returns" Infrastructures 5, no. 2: 13. https://doi.org/10.3390/infrastructures5020013
APA StyleOyegbile, O. B., & Chorzepa, M. G. (2020). Co-Active Prioritization by Means of Contingency Tables for Analyzing Element-level Bridge Inspection Results and Optimizing Returns. Infrastructures, 5(2), 13. https://doi.org/10.3390/infrastructures5020013