Intrinsic Thermal Shock Behavior of Common Rutile Oxides
Abstract
:1. Introduction
2. Methods
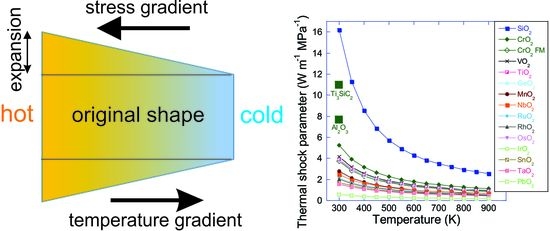
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baur, W.H. Rutile-type compounds. Acta Cryst. B 1976, 32, 2200. [Google Scholar] [CrossRef]
- Maddox, B.R.; Yoo, C.S.; Kasinathan, D.; Pickett, W.E.; Scalettar, R.T. High-pressure structure of half-metallic CrO2. Phys. Rev. B 2006, 73, 144111. [Google Scholar] [CrossRef]
- Pascual, J.; Camassel, J.; Mathieu, H. Fine structure in the intrinsic absorption edge of TiO2. Phys. Rev. B 1978, 18, 5606. [Google Scholar] [CrossRef]
- Lee, J.M.; Shin, J.C.; Hwang, C.S.; Kim, H.J.; Suk, C.-G. Preparation of high quality RuO2 electrodes for high dielectric thin films by low pressure metal organic chemical vapor deposition. J. Vac. Sci. Technol. A 1998, 16, 2768. [Google Scholar] [CrossRef]
- O’Hara, A.; Nunley, T.N.; Posadas, A.B.; Zollner, S.; Demkov, A.A. Electronic and optical properties of NbO2. J. Appl. Phys. 2014, 116, 213705. [Google Scholar] [CrossRef]
- Joshi, T.; Senty, T.R.; Borisov, P.; Bristow, A.D.; Lederman, D. Preparation, characterization, and electrical properties of epitaxial NbO2 thin film lateral devices. J. Phys. D Appl. Phys. 2015, 48, 335308. [Google Scholar] [CrossRef]
- Bolzan, A.A.; Fong, C.; Kennedy, B.J.; Howard, C.J. A powder neutron diffraction study of semiconducting and metallic niobium dioxide. J. Solid State Chem. 1994, 113, 9. [Google Scholar] [CrossRef]
- Qazilbash, M.M.; Brehm, M.; Chae, B.-G.; Ho, P.-C.; Andreev, G.O.; Kim, B.-J.; Yun, S.J.; Balatsky, A.V.; Maple, M.B.; Keilmann, F.; et al. Mott transition in VO2 revealed by infrared spectroscopy and nano-imaging. Science 2007, 318, 1750. [Google Scholar] [CrossRef]
- Lu, T.J.; Fleck, N.A. The thermal shock resistance of solids. Acta Mater. 1998, 46, 4755. [Google Scholar] [CrossRef]
- Rao, C.N.R. Transition metal oxides. Annu. Rev. Phys. Chem. 1989, 40, 291. [Google Scholar] [CrossRef]
- Saidi, H.; Roudini, G.; Afarani, M.S. High-volume-fraction Cu/Al2O3-SiC hybrid interpenetrating phase composite. Appl. Phys. A 2015, 121, 109. [Google Scholar] [CrossRef]
- Xin, D.Y.; Komatsu, K.; Abe, K.; Costa, T.; Ikeda, Y.; Nakamura, A.; Ohshio, S.; Saitoh, H. Heat-shock properties in yttrium-oxide films synthesized from metal-ethylenediamine tetraacetic acid complex through flame-spray apparatus. Appl. Phys. A 2017, 123, 194. [Google Scholar] [CrossRef]
- Case, E.D. Thermal fatigue and waste heat recovery via thermoelectrics. J. Electron. Mater. 2012, 41, 1811. [Google Scholar] [CrossRef]
- Krupke, W.F.; Shinn, M.D.; Marion, J.E.; Caird, J.A.; Stokowski, S.E. Spectroscopic, optical, and thermomechanical properties of neodymium- and chromium-doped gadolinium scandium gallium garnet. J. Opt. Soc. Am. B 1986, 3, 102. [Google Scholar] [CrossRef]
- Music, D.; Bliem, P.; Hans, M. Holistic quantum design of thermoelectric niobium oxynitride. Solid State Commun. 2015, 212, 5. [Google Scholar] [CrossRef]
- Music, D.; Geyer, R.W.; Schneider, J.M. Recent progress and new directions in density functional theory based design of hard coatings. Surf. Coat. Technol. 2016, 286, 178. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Slack, G.A. Nonmetallic crystals with high thermal conductivity. J. Phys. Chem. Solids 1973, 34, 321. [Google Scholar] [CrossRef]
- Söderlind, P.; Nordström, L.; Yongming, L.; Johansson, B. Relativistic effects on the thermal expansion of the actinide elements. Phys. Rev. B 1990, 42, 4544. [Google Scholar] [CrossRef] [PubMed]
- El-Raghy, T.; Barsoum, M.W.; Zavaliangos, A.; Kalidini, S.R. Processing and mechanical properties of Ti3SiC2: II, effect of grain size and deformation temperature. J. Am. Ceram. Soc. 1999, 82, 2855. [Google Scholar] [CrossRef]
- Feng, B.; Li, Z.; Zhang, X. Prediction of size effect on thermal conductivity of nanoscale metallic films. Thin Solid Films 2009, 517, 2803. [Google Scholar] [CrossRef]
- Music, D.; Kremer, O.; Pernot, G.; Schneider, J.M. Designing low thermal conductivity of RuO2 for thermoelectric applications. Appl. Phys. Lett. 2015, 106, 063906. [Google Scholar] [CrossRef]
- Daniel, R.; Holec, D.; Bartosik, M.; Keckes, J.; Mitterer, C. Size effect of thermal expansion and thermal/intrinsic stresses in nanostructured thin films: Experiment and model. Acta Mater. 2011, 59, 6631. [Google Scholar] [CrossRef]
- Zhang, J.; Estévez, D.; Zhao, Y.-Y.; Huo, L.; Chang, C.; Wang, X.; Li, R.-W. Flexural strength and Weibull analysis of bulk metallic glasses. J. Mater. Sci. Technol. 2016, 32, 129. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal-amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14271. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [Green Version]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA: A three-dimensional visualization system for electronic and structural analysis. J. Appl. Cryst. 2008, 41, 653. [Google Scholar] [CrossRef]
- Morelli, D.T.; Heremans, J.P. Thermal conductivity of germanium, silicon, and carbon nitrides. Appl. Phys. Lett. 2002, 81, 5126. [Google Scholar] [CrossRef]
- Sanditov, B.D.; Tsydypov, S.B.; Sanditov, D.S. Relation between the Grüneisen constant and Poisson’s ratio of vitreous systems. Acoust. Phys. 2007, 53, 594. [Google Scholar] [CrossRef]
- Wang, H.-F.; Chu, W.-G.; Guo, Y.-J.; Jin, H. Thermal transport property of Ge34 and d-Ge investigated by molecular dynamics and the Slack’s equation. Chin. Phys. B 2010, 19, 076501. [Google Scholar] [CrossRef]
- Sun, Z.; Li, S.; Ahuja, R.; Schneider, J.M. Calculated elastic properties of M2AlC (M = Ti, V, Cr, Nb and Ta). Solid State Commun. 2004, 129, 589. [Google Scholar] [CrossRef]
- Mehl, M.J.; Osburn, J.E.; Papaconstantopoulos, D.A.; Klein, B.M. Structural properties of ordered high-melting-temperature intermetallic alloys from first-principles total-energy calculations. Phys. Rev. B 1990, 41, 10311. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. Lond. 1952, 65, 349. [Google Scholar] [CrossRef]
- Music, D.; Geyer, R.W.; Keuter, P. Thermomechanical response of thermoelectrics. Appl. Phys. Lett. 2016, 109, 223903. [Google Scholar] [CrossRef]
- Evertz, S.; Music, D.; Schnabel, V.; Bednarcik, J.; Schneider, J.M. Thermal expansion of Pd-based metallic glasses by ab initio methods and high energy x-ray diffraction. Sci. Rep. 2017, 7, 15744. [Google Scholar] [CrossRef]
- Birch, F. Finite strain isotherm and velocities for single-crystal and polycrystalline NaCl at high pressures and 300 K. J. Geophys. Res. 1978, 83, 1257. [Google Scholar] [CrossRef]
- Blanco, M.A.; Pendás, A.M.; Francisco, E.; Recio, J.M.; Franco, R. Thermodynamical properties of solids from microscopic theory: Applications to MgF2 and Al2O3. J. Mol. Struct. 1996, 368, 245. [Google Scholar] [CrossRef]
- Rao, K.V.K.; Naidu, S.V.N.; Iyengar, L. Thermal expansion of rutile and anatase. J. Am. Ceram. Soc. 1970, 53, 124. [Google Scholar] [CrossRef]
- Kim, D.J.; Kim, D.S.; Cho, S.; Kim, S.W.; Lee, S.H.; Kim, J.C. Measurement of thermal conductivity of TiO2 thin films using 3ω method. Int. J. Thermophys. 2004, 25, 281. [Google Scholar] [CrossRef]
- Wu, M.; Liang, Y.; Jiang, J.-Z.; Tse, J.S. Structure and properties of dense silica glass. Sci. Rep. 2012, 2, 398. [Google Scholar] [CrossRef] [PubMed]
- Scanlon, D.O.; Kehoe, A.B.; Watson, G.W.; Jones, M.O.; David, W.I.F.; Payne, D.J.; Egdell, R.G.; Edwards, P.P. Nature of the band gap and origin of the conductivity of PbO2 revealed by theory and experiment. Phys. Rev. Lett. 2011, 107, 246402. [Google Scholar] [CrossRef] [PubMed]
- Nordling, C.; Österman, J. Physics Handbook for Science and Engineering; Studentlitteratur: Lund, Sweden, 1996. [Google Scholar]
- Bodnar, I.V. Thermal expansion and thermal conductivity of In2S3 and CuIn5S8 compounds and (CuIn5S8)1−x(In2S3)x alloys. Semiconductors 2014, 48, 557. [Google Scholar] [CrossRef]
- Munro, R.G. Material properties of a sintered α-SiC. J. Phys. Chem. Ref. Data 1997, 26, 1195. [Google Scholar] [CrossRef]
- Talwar, D.N.; Sherbondy, J.C. Thermal expansion coefficient of 3C-SiC. Appl. Phys. Lett. 1995, 67, 3301. [Google Scholar] [CrossRef]
- Roder, C.; Einfeldt, S.; Figge, S.; Hommel, D. Temperature dependence of the thermal expansion of GaN. Phys. Rev. B 2005, 72, 085218. [Google Scholar] [CrossRef]
- Shibata, H.; Waseda, Y.; Ohta, H.; Kiyomi, K.; Shimoyama, K.; Fujito, K.; Nagaoka, H.; Kagamitani, Y.; Simura, R.; Fukuda, T. High thermal conductivity of gallium nitride (GaN) crystals grown by HVPE process. Mater. Trans. 2007, 48, 2782. [Google Scholar] [CrossRef]
- Pavlova, L.M.; Shtern, Y.I.; Mironov, R.E. Thermal expansion of bismuth telluride. High Temp. 2011, 49, 369. [Google Scholar] [CrossRef]
- Tian, Z.; Garg, J.; Esfarjani, K.; Shiga, T.; Shiomi, J.; Chen, G. Phonon conduction in PbSe, PbTe, and PbTe1-xSex from first-principles calculations. Phys. Rev. B 2012, 85, 184303. [Google Scholar] [CrossRef]
- Ouyang, T.; Hu, M. Competing mechanism driving diverse pressure dependence of thermal conductivity of XTe (X = Hg, Cd, and Zn). Phys. Rev. B 2015, 92, 235204. [Google Scholar] [CrossRef]
- Albertsson, J.; Abrahms, S.C. Atomic displacement, anharmonic thermal vibration, expansivity and pyroelectric coefficient thermal dependences in ZnO. Acta Cryst. B 1989, 45, 34. [Google Scholar] [CrossRef]
- Xu, Y.; Goto, M.; Kato, R.; Tanaka, Y.; Kagawa, Y. Thermal conductivity of ZnO thin film produced by reactive sputtering. J. Appl. Phys. 2012, 111, 084320. [Google Scholar] [CrossRef]
- Ligny, D.D.; Richet, P. High-temperature heat capacity and thermal expansion of SrTiO3 and SrZrO3 perovskites. Phys. Rev. B 1996, 53, 3013. [Google Scholar] [CrossRef]
- Yu, C.; Scullin, M.L.; Huijben, M.; Ramesh, R.; Majumdar, A. Thermal conductivity reduction in oxygen-deficient strontium titanates. Appl. Phys. Lett. 2008, 92, 191911. [Google Scholar] [CrossRef]
- Tong, H.M.; Hsuen, H.K.D.; Saenger, K.L.; Su, G.W. Thickness-direction coefficient of thermal expansion measurement of thin polymer films. Rev. Sci. Instrum. 1991, 62, 422. [Google Scholar] [CrossRef]
- Al-Ghamdi, A.A.; Al-Salamy, F.; Al-Hartomy, O.A.; Al-Ghamdi, A.A.; Daiem, A.M.A.; El-Tantawy, F. Thermophysical properties of foliated graphite/nickel reinforced polyvinyl chloride nanocomposites. J. Appl. Polym. Sci. 2012, 124, 1144. [Google Scholar] [CrossRef]
- Yue, S.-Y.; Qin, G.; Zhang, X.; Sheng, X.; Su, G.; Hu, M. Thermal transport in novel carbon allotropes with sp2 or sp3 hybridization: An ab initio study. Phys. Rev. B 2017, 95, 085207. [Google Scholar] [CrossRef]
- Liu, H.; Qin, G.; Lin, Y.; Hu, M. Disparate strain dependent thermal conductivity of twodimensional penta-structures. Nano Lett. 2016, 16, 3831. [Google Scholar] [CrossRef] [PubMed]
- Shojaee, E.; Mohammadizadeh, M.R. First-principles elastic and thermal properties of TiO2: A phonon approach. J. Phys. Condens. Matter 2010, 22, 015401. [Google Scholar] [CrossRef] [PubMed]
- Bohnen, K.-P.; Heid, R.; de la Pena Seaman, O.; Renker, B.; Adelmann, P.; Schober, H. Lattice dynamics of RuO2: Theory and experiment. Phys. Rev. B 2007, 75, 092301. [Google Scholar] [CrossRef]
- Isaak, D.G.; Carnes, J.D.; Anderson, O.L.; Cynn, H.; Hake, E. Elasticity of TiO2 rutile to 1800 K. Phys. Chem. Minerals 1998, 26, 31. [Google Scholar] [CrossRef]
- Haines, J.; Léger, J.M.; Hoyau, S. Second-order rutile-type to CaCl2-type phase transition in β-MnO2 at high pressure. J. Phys. Chem. Solids 1995, 56, 965. [Google Scholar] [CrossRef]
- Haines, J.; Léger, J.M.; Pereira, A.S.; Häusermann, D.; Hanfland, M. High-pressure structural phase transitions in semiconducting niobium dioxide. Phys. Rev. B 1999, 59, 13650. [Google Scholar] [CrossRef]
- Zheng, J.-C. Superhard hexagonal transition metal and its carbide and nitride: Os, OsC, and OsN. Phys. Rev. B 2005, 72, 052105. [Google Scholar] [CrossRef]
- Ono, S.; Kikegawa, T.; Ohishi, Y. High-pressure and high-temperature synthesis of a cubic IrO2 polymorph. Physica B 2005, 363, 140. [Google Scholar] [CrossRef]
- Grocholski, B.; Shim, S.-H.; Cottrell, E.; Prakapenka, V.B. Crystal structure and compressibility of lead dioxide up to 140 GPa. Am. Mineral. 2014, 99, 170. [Google Scholar] [CrossRef]
- Ross, N.L.; Shu, J.-F.; Hazen, R.M.; Gasparik, T. High-pressure crystal chemistry of stishovite. Am. Mineral. 1990, 75, 739. [Google Scholar]
- Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, I.C.; Ángyán, J.G. Screened hybrid density functionals applied to solids. J. Chem. Phys. 2006, 124, 154709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Burdett, J.K.; Hughbanks, T.; Miller, G.J.; Richardson, J.W., Jr.; Smith, J.V. Structural-electronic relationships in inorganic solids: Powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K. J. Am. Chem. Soc. 1987, 109, 3639. [Google Scholar] [CrossRef]
- Zhang, H.B.; Zhou, Y.C.; Bao, Y.W.; Li, M.S. Abnormal thermal shock behavior of Ti3SiC2 and Ti3AlC2. J. Mater. Res. 2006, 21, 2401. [Google Scholar] [CrossRef]
- Barsoum, M.W.; Radovic, M. Elastic and mechanical properties of the MAX phases. Annu. Rev. Mater. Res. 2011, 41, 195. [Google Scholar] [CrossRef]
- Chen, H.C.; Pfender, E.; Heberlein, J. Plasma-sprayed ZrO2 thermal barrier coatings doped with an appropriate amount of SiO2. Thin Solid Films 1998, 315, 159. [Google Scholar] [CrossRef]





© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Music, D.; Stelzer, B. Intrinsic Thermal Shock Behavior of Common Rutile Oxides. Physics 2019, 1, 290-300. https://doi.org/10.3390/physics1020022
Music D, Stelzer B. Intrinsic Thermal Shock Behavior of Common Rutile Oxides. Physics. 2019; 1(2):290-300. https://doi.org/10.3390/physics1020022
Chicago/Turabian StyleMusic, Denis, and Bastian Stelzer. 2019. "Intrinsic Thermal Shock Behavior of Common Rutile Oxides" Physics 1, no. 2: 290-300. https://doi.org/10.3390/physics1020022
APA StyleMusic, D., & Stelzer, B. (2019). Intrinsic Thermal Shock Behavior of Common Rutile Oxides. Physics, 1(2), 290-300. https://doi.org/10.3390/physics1020022