Integrated Braking Control for Electric Vehicles with In-Wheel Propulsion and Fully Decoupled Brake-by-Wire System

Abstract

This paper introduces a case study on the potential of new mechatronic chassis systems for battery electric vehicles, in this case a brake-by-wire (BBW) system and in-wheel propulsion on the rear axle combined with an integrated chassis control providing common safety features like anti-lock braking system (ABS), and enhanced functionalities, like torque blending. The presented controller was intended to also show the potential of continuous control strategies with regard to active safety, vehicle stability and driving comfort. Therefore, an integral sliding mode (ISM) and proportional integral (PI) control were used for wheel slip control (WSC) and benchmarked against each other and against classical used rule-based approach. The controller was realized in MatLab/Simulink and tested under real-time conditions in IPG CarMaker simulation environment for experimentally validated models of the target vehicle and its systems. The controller also contains robust observers for estimation of non-measurable vehicle states and parameters e.g., vehicle mass or road grade, which can have a significant influence on control performance and vehicle safety.

1. Introduction

Electric vehicles (EVs) with individually controlled in-wheel motors (IWMs) are receiving more and more attention by the automotive industry and in research due to their high performance, design flexibility and other factors addressing requirements of transportation electrification and automation. One of the most attractive but also challenging features of EVs with in-wheel propulsion is the possibility of blended operation of the friction brake system and the regenerative brake system (represented by IWMs working in a generator mode) that can essentially improve energy efficiency, fail-safety, and motion control performance in critical driving situations. To realize such blended operation, the friction brake system should preferably have a decoupled architecture, where the connection between the driver and brake callipers is realized through the brake pedal simulator, and the callipers can be individually controlled with precisely metered clamping force. Such decoupling is an inherent feature of most brake-by-wire systems.

BBW systems can be implemented with electro-hydraulic [1,2,3], electro-mechanical [4,5,6], or, rarely, magnetorheological [7] actuators as well as with hybrid actuation [8,9,10]. Electro-hydraulic brakes (EHBs) and electro-mechanical brakes (EMBs) are using different methods to control the clamping forces generating the friction contact between the brake pad and the brake disc. However, there are still no well-established approaches in this regard.

As for EHBs, relevant studies often propose various options of pulse-width modulation (PWM) for controlling the valves, for instance, closed-loop pressure-difference-limiting modulation [11] and current amplitude modulation [12], usually supplemented with rule-based control for the brake pressure modes (increase, decrease and hold). One of the commonly observed problems by the EHB operations relates to undesirable pressure peaks and oscillations that can be caused, for example, by misalignment between the clamping force control and the anti-lock braking system (ABS) control. Therefore, relevant attenuation mechanisms, such as model-based friction compensation can be included in the EHB control loop [13].

A variety of clamping force control methods can also be found in studies on electro-mechanical BBW systems. For instance, the work [14] illustrated an EMB design with permanent magnet synchronous motor and planetary gear, where the clamping force is being estimated using recursive least square approach and then controlled with the adaptive sliding mode control. Another variant with the brain limbic system-based method and the genetic algorithm in [15]. As for EMBs, the clamping force control has also to consider minimization of the energy consumption by actuators [16] and the brake judder [17].

BBW design should pay proper attention not only to the clamping force control but also to the brake blending procedures to address efficient and reliable joint operation of electric motors and friction brakes. In this regard various studies propose to use variable structure control [18], sliding mode control with switching compensation [19], optimal predictive control [20], and fuzzy logic [20,21]. However, most of known brake blending procedures are still using rule-based control due to such factors as real-time applicability and fault-tolerance. The same statement is valid for the ABS/wheel slip control systems of electric vehicles with friction and regenerative actuators [22]. Nevertheless, recent advancements in control techniques are proposing more and more robust real-time-capable continuous control methods that allow their consideration by designing integrated braking control [23].

In line with the presented aspects, this paper introduces an approach for integrated braking control with a hybrid BBW design for a vehicle, in whichthe front axle is equipped with EHBs and the rear axle uses EMBs [24]. Additionally, the advantages of continuous control approaches are investigated. The next sections of the paper outline the system architecture, the main elements of the controller design, and validation of the system in the real-time model-in-the-loop environment.

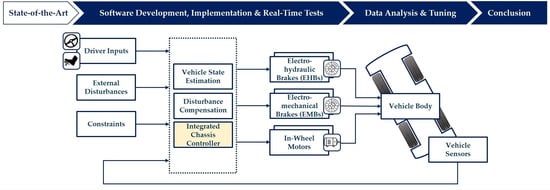
2. Description of the Mechatronic Systems

The target vehicle, discussed in this study, uses a hybrid brake-by-wire system of Brembo Company (Stezzano, Italy). Figure 1 shows the hydraulic circuit of the electro-hydraulic callipers in the front and the wiring to the electro-mechanical sliding callipers in the rear, including all applied sensors and control units. The indices FL, FR, RL, and RR indicate the front left, front right, rear left, and rear right corners, respectively.

The driver’s brake demand is measured via stroke sensors. In order to be fail-safe, the system uses two redundant stroke sensors. Through the pressure sensor, the vehicle control unit (VCU) can make a plausibilization between stroke and pressure, increasing the redundancy and reliability of the system. Within the VCU, the brake demand is converted into an equivalent torque demand and distributed to the corners as defined by the incorporated electronic brake force distribution (EBD). Therefore, K_f and K_r are introduced as factors for torque-to-pressure- and torque-to-force-transmission for generation of the input signals for the EHB and the EMB, respectively. Those signals are transmitted by the braking control units (BCUs).

$$K_f=\frac{1}{{2\mu }_{br}{A}_{pist}{R}_{disc}}=\frac{K_r}{A_{pist}}$$

(1)

Table 1. Main parameters of the brake-by-wire system used.

Symbol	Description	Value	Unit
Rdisc	Effective brake disc radius	0.167	m
APist	Cross-section of brake caliper piston	317.615	mm2
µbr	Brake disc-to-pad friction coefficient	0.43	-

shows the parameter values for the system used, for which K_f = 0.02 bar/Nm and K_r = 6.963 N/Nm.

The used, hybrid brake-by-wire system originally incorporates blending functionality, but without any switching valves, as typically used in centralized systems, its distributed architecture allows individual and continuous control of the clamping force (or pressure) over the four corners. The dynamics of the system are shown by the transfer function in Figure 2. It can be seen, that the maximum modulation frequency is about 12–13 Hz, which is mainly based on the characteristics of the electro-mechanical components and software calibration and has to be considered in the controller design.

Besides the decoupled braking system, the target vehicle is equipped with in-wheel machines on the rear axle, see Figure 3, provided by Elaphe Propulsion Technologies Ltd. (Ljubljana, Slovenia). The machines used are based on liquid-cooled synchronous machines with a maximum power of 110 kW and a maximum torque of 1.500 Nm in boost mode. Additionally, they are designed for a wide range of vehicular applications such as sedans, SUVs, pick-ups or small cargo trucks. The knuckle adapter fits most vehicles on the market, enabling easy implementation. It also includes a friction brake device with Electronic Parking Brake (EPB), which was replaced in the presented application to install the electro-mechanical sliding callipers from Brembo.

Contrary to classical electric drivetrains, this type of electric drive is connected directly to the wheels, which has many advantages in terms of weight, packaging and efficiency. As shown in the efficiency map plot (Figure 4), the power is transmitted with efficiencies up to 95%. Moreover, it also allows a highly dynamic actuation, which makes it interesting for vehicle control engineering, especially compared to the brake system’s dynamics, see Figure 2.

3. Observer Design

Even if many sensors in modern vehicles are able to measure different signals, there are also some parameters that cannot be quantified directly or only with high technical and cost efforts. As some of these non-measurable parameters are quite important for vehicle dynamics control, these parameters are estimated instead, which means that they are calculated from other known values or measured signals in combination with physical laws or geometrical dependencies. Here, vehicle mass and road slope observers are presented, since Equation (5) shows, that vehicle mass is linked directly to the calculation of the torque demand and the road slope generates an additional resistance (see Equation (2)), which also needs to be considered.

Using the second Newtonian approach the equilibrium of longitudinal forces is given by Equation (2) where m_v is the vehicle’s total mass, v_x is the longitudinal velocity, F_d and F_air are the driving and air drag force, respectively, g is the gravitational acceleration and χ is the road slope angle.

$$m_v{\stackrel{·}{v}}_x=\underset{≔F_d}{\underbrace{T_d{r}_w}}-\underset{≔F_{air}}{\underbrace{\frac{1}{2}{c}_w{\rho }_{air}{A}_v{v}_{air}{}^2}}-\underset{≔F_{slope}}{\underbrace{m_{v}gsin\left(\chi \right)}}$$

(2)

Assuming that the vehicle is equipped with an inertial measurement unit (IMU), a_x as longitudinal acceleration and g are measurable directly on flat road. However, every time the vehicle drives up- or downhill, the signal of a_x is overlaid by a gravitational component, reflected by the measurement signal a_IMU, see [25]. Hence, the real acceleration is higher or lower than the measured one. With this knowledge, Equation (2) can be modified.

$$m_v\underset{≔a_{\mathit{IMU}}}{\underbrace{\left({\stackrel{·}{v}}_x+g\mathit{sin}\left(\chi \right)\right)}}{=F}_d-F_{air}$$

(3)

Considering that the linear system with unknown parameter θ (see Equation (4)) and coefficient matrix X can be solved for every time step k via a discrete recursive least squares algorithm (RLSA), vehicle mass estimation is set to y = [F_d − F_air], X = a_IMU and θ = m_v, while the RLSA problem for road slope contains y = [a_IMU − a_x], X = g and θ = sin(χ).

$$y_k{=X}_k{\theta }_k$$

(4)

To avoid quick oscillations in the estimated states, the forgetting factor is set to 0.9995 and additionally combined with high a gain derivative with a 2 Hz cut-off frequency.

For optimal performance, some additional specifications are made below:

i

The observer becomes inactive if the steering angle (δ_SW, see Figure 5) or the corresponding yaw rate ($\dot{\psi }$) exceeds a fixed threshold because of its inability to account for inertial components associated with cornering.

ii

At vehicle speeds under 5 km/h, the vehicle mass observer is switched off to avoid unnecessary noise.

iii

Solving Equation (3) requires the driving force, so observation of vehicle mass is only active when the gas pedal displacement exceeds a minimum of 20%.

iv

Upon exceeding a minimum gas pedal position, the wheel load observer becomes inactive, provided that no excessive wheel slip is detected.

Figure A1 shows the functionality of the developed observers for acceleration/deceleration maneuvres with multiple slopes. It can be seen that the estimation follows the real values quite well. The vehicle mass especially remains stable, as the small offset between the estimated and real values is related to uncertainties of the virtual sensors.

4. Controller Design

To bring the benefits and functionality of the drivetrain and brake system together, a suitable control strategy is needed. Therefore, a combined and integrated controller was developedthat was able to provide common safety functions, such ABS and was also enhanced by functionalities such as regenerative braking through the IWMs. The present article was intended as a case study for the adaptation of the outcomes of [22,23,26] to the new, mechatronic systems. Figure 5 shows the controller structure as a block scheme.

Since the vehicle is driven by a human, the first signals are the driver inputs, given by the pedal application force (F_Ped) and the steering wheel torque (T_SW), whichcausing a pedal displacement (s_ped) or an angular displacement, namely the steering wheel angle (δ_SW). Of course, both signals also display the parameters of the driver feedback, which informs the driver about e.g., road irregularities or changing friction conditions.

4.1. Base Brake Controller

Right after the detection of the driver inputs, the base brake controller converts the brake pedal displacement into a corresponding torque request T_dem. Equation (5) contains the mathematical description, where r_w is the wheel radius and a_ref describes the reference deceleration that relates to the pedal feel characteristic as shown for the target vehicle in Figure 6.

$$T_{\mathit{dem}}{=m}_v{a}_{\mathit{ref}}{r}_w$$

(5)

Normally, these characteristics strongly depend on the parameters of the hydraulic components, especially pipe diameters and lengths. Since these investigations concern a BBW system, the pedal feeling is generated by the pedal simulator artificially. In case of system failure (e.g., power loss), all valves open up, so that there is a direct hydraulic linkage between the master cylinder and the front actuators. The pedal simulator becomes inactive and the pedal feel is as for a hydraulic system without the brake booster’s support.

After generation of the total torque demand, this amount has to be distributed to the corners. Equation (6) shows the ideal torque allocation assuming the utilization of both axles

$${\mathit{fi}}_{\mathit{id}}=\frac{a_x}{g}\left(\frac{h}{L}+\frac{1}{z}\frac{l_r}{L}\right){=\mu }_f\left(\frac{h}{L}+\frac{1}{z}\frac{l_r}{L}\right)$$

(6)

where h is the height of the center of gravity (COG), L is the vehicle’s wheel base, l_r is the distance between rear axle and the COG along the vehicle’s x-axis, z is the braking intensity as defined in [27] and µ_f is the friction coefficient in the tire road contact point of the front axle, which should be satisfied as in Equation (7) to avoid early lock of the rear wheels.

$${\mu }_f<\frac{1}{0.85}\left(\frac{a_x}{g}+0.07\right)$$

(7)

Since the front axles usually carry a greater load caused by the dynamic wheel loads while braking, Equation (7) can be included in Equation (6). As F_x,max = µ_maxF_z and µ_f > µ_r, the formula can then be rewritten in the form of Equation (8) as the formulation for the best tire-road friction conditions of the front-to-total constraint fi_grip. This parameter is used to split the total demand onto the wheels (T_dem^ij), where i stands for the axle (front, rear) and j for the side (left, right).

$${\mathit{fi}}_{\mathit{grip}}{=1+\mu }_{\mathit{max}}\left(\frac{h}{L}+\frac{1}{z}\frac{l_r}{L}\right)$$

(8)

4.2. Torque Blending Controller

The target vehicle utilizes in-wheel propulsion, which can be used for deceleration while the electric machines are running in generator mode. This recovers kinetic energy which is usable for re-charging the battery e.g., to enhance the mileage. If the requested electric motor torque T_dem,EM is higher than the maximum achievable electric torque T_max,EM, friction brakes are activated parallel to the electric machines (T_dem,FB) to increase the wheel torque (T_w) up to the total requested amount (T_WSC). The torque blending control serves as the coordinator and supervisor of this procedure. Therefore, the blending factor α is introduced, which defines the level at which the actuators should intervene at every corner: parallel phasing is used if 0 < α^ij < 1 and series phasing if α^ij = 1. Both methods are depicted in Figure A2.

$$\left[\begin{array}{c}{T}_{\mathit{dem},\mathit{EM}}{}^{ij}\\ T_{\mathit{dem},\mathit{FB}}{}^{ij}\end{array}\right]=\left[\begin{array}{c}{\mathrm{sat}}_0^{T_{\mathit{max},\mathit{EM}}{}^{ij}}{(\alpha }^{ij}{T}_{\mathit{WSC}}{}^{ij})\\ \begin{array}{c}\\ (1-{\alpha }^{ij}{)T}_{\mathit{WSC}}{}^{ij}+\underset{\mathrm{ECE}13\mathrm{H}}{\underbrace{{(T}_{\mathit{dem},\mathit{EM}}{}^{ij}-T_{\mathit{dem},\mathit{FB}}{}^{ij})}}\end{array}\end{array}\right]$$

(9)

The implemented algorithm can also consider limiting parameters to limit the torque demand after wheel slip correction (T_WSC^ij):

i

Battery state of X (SOX): in particular, the charging current (I_B) and cell voltages are used for prediction of the state of charge (SOC).

ii

Vehicle speed (v_x) at higher speeds, the maximum electric torque is reduced by power restrictions and, at low speeds, only friction torque is usedas energy recuperation is not provided.

iii

Motor/battery temperature (θ_EM, θ_B): it might be necessary to reduce the electric motor torque request to avoid excessive overheating of components.

According to all these limitations, the blending factor α is changed. Figure A3 shows the results for a test run in a real-time environment with a parallel phasing at α = 0.75 for reaching the speed and SOC limit. (The temperature limit was not implemented, due to boundaries of the battery model for simulation of heating/cooling processes).

In compliance with [28] it is worth noticing that, upon reaching saturation on the electric motors, friction brakes are activated independently of the chosen phasing. To smooth out the transition between friction brakes and electric motors, a first order filter with 5 Hz cut-off corrects the blending factor to be sent to the controller.

4.3. Wheel Slip Controller

Wheel slip describes the deviation of the wheels’ speed (ω^ij) at the tire road contact point compared to the vehicle speed see Equation (10), where r_dyn^ij is the dynamic wheel radius of the loaded wheel after one full rotation.

$${\lambda }_x{}^{ij}=\frac{v_x-v_w}{v_x}=\frac{v_x-{\omega }^{ij}{r}_{\mathit{dyn}}{}^{ij}}{v_x}$$

(10)

Wheel slip control systems are quite important for driving safety to suppress excessive skidding (λ < 0) and spinning (λ > 0) of the wheel during braking (ABS) or driving (traction control, TC) maneuvers, respectively. To do this, the controller becomes activated every time the slip exceeds a fixed threshold, named the reference slip λ_ref^ij, and stays active, until the driver input on the brake or accelerator pedal disappears. To get the slip under the threshold again, the demanded torque is corrected by a so-called reactive component (T_react^ij). Related to the statements and results in [26], the WSC presented in this paper involves a comparison between the continuous approaches of integral sliding mode control with classical PI control. Latter one will be introduced first.

4.3.1. Proportional Integral Control with Anti-Windup

Proportional integral (PI) control is very easy to implement. Normally, an additional derivative part is included to suppress any upswing of the output signal. In the present case, this derivative part is ignored because it makes the controller more sensitive to noise. The implemented anti-windup part compensates the integral component if the control error saturates, but otherwise it is inactive. Equation (11) defines this error as the difference between the real and reference slip. Because the slip cannot be measured directly, it is marked as estimation value by the hat index.

$${\lambda }_e=\{\begin{array}{c}\hat{\lambda }-{\lambda }_{\mathit{ref}}\mathit{if}\mathit{WSC}\mathit{is}\mathit{activated}\\ \hspace{0.17em}0\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathit{else}\hfill \end{array}$$

(11)

The defined error is the input for the wheel slip controller and leads to the general PI control law given by

$$u_{\mathit{PI}}{(\lambda }_e{)=K}_P{\lambda }_e+\int \left[\frac{K_P{\lambda }_e}{{\tau }_i}-\frac{1}{{\tau }_a}\left[u_{\mathit{PI}}-{\mathrm{sat}}_0^{u_{\mathit{max}}}{(u}_{\mathit{PI}})\right]\right]d\tau$$

(12)

where K_P is the proportional gain, τ_i the time constant of integral, and τ_a the time constant of the anti-windup part. Even if this control provides good results, there was nevertheless a second approach realized for benchmarking purposes.

4.3.2. Integral Sliding Mode Control

The integral sliding mode (ISM) control provides a potentially better performance than the presented PI control, because the ISM combines the advantages of the integral part for smooth tracking of the reference slip with the fast switching control of the sliding mode approach. In summary, this should guarantee much more accurate error compensation with less chattering effects. Equation (13) shows the control law for ISM control, which is given by a continuous and a discontinuous part, with the continuous part equaling the presented PI control.

$$u_{\mathit{ISM}}{=u}_c{+u}_d$$

(13)

$$u_d=-K_{\mathit{ISM}}\mathrm{sign}\left(s\right)$$

(14)

The discontinuous part can be described by Equation (14) where s is the sliding surface given by the sliding variable s₀ = λ_e (see Equation (11)) and an integral part

$${\stackrel{·}{z}}_{\mathit{ISM}}{=\stackrel{·}{\lambda }}_{\mathit{ref}}-{B(u}_{\mathit{ISM}}-u_d)$$

(15)

where input matrix B has its origin in the quarter dynamics vehicle model formulation of the wheel slip as given by

$$\stackrel{·}{\lambda }=-\frac{1}{v_x}\left(\frac{1-\lambda }{m_w}+\frac{r_w{}^2}{J_w}\right)F_x\left(\lambda \right)+\frac{r_w}{J_w{v}_x}{T}_w$$

(16)

where m_w is the unsprung mass, r_w the wheel’s radius, J_w the inertia of the wheel, F_x the longitudinal wheel force(s) and the applied torque T_w as the controller’s output (u_ISM).

Assuming that (1 − λ)m⁻¹ << r_w²J_w and that all brake system related uncertainties can be summarized in a parameter T_unc, Equation (16) comes to

$$\widehat{\stackrel{·}{\lambda }}\approx -\underset{B}{\underbrace{\frac{r_w}{J_w{v}_x}}}{r}_w{F}_x\left(\hat{\lambda }\right)+\underset{B}{\underbrace{\frac{r_w}{J_w{v}_x}}}\underset{u_{\mathit{ISM}}}{(\underbrace{T_w}}{+T}_{\mathit{unc}}).$$

(17)

To avoid control degradation caused by estimation uncertainties, the system uncertainty h = −B(r_wF_x($\hat{\lambda }$) − T_unc) is introduced; so Equation (17) becomes

$$\widehat{\stackrel{·}{\lambda }}{=h+\mathit{BT}}_w{=h+\mathit{Bu}}_{\mathit{ISM}}.$$

(18)

To reduce the chattering, the discontinuous part is low-pass filtered, described by the following expression where τ_f is the time constant of first order filter.

$$u_{d,\mathit{filt}}{=\stackrel{·}{u}}_{d,\mathit{filt}}{\tau }_f {+u}_d$$

(19)

Proof of stability leads to Equation (20) which can be solved by adding Equation (18).

$$\dot{V}=\frac{s}{2}\left[\underset{{\dot{s}}_0}{\underbrace{\widehat{\dot{\lambda }}-{\dot{\lambda }}_{\mathit{ref}}}}+\underset{{\stackrel{·}{z}}_{\mathit{ISM}}}{\underbrace{{\dot{\lambda }}_{\mathit{ref}}-{B(u}_{\mathit{ISM}}{+K}_{\mathit{ISM}}\mathrm{sign}\left(s\right))}}\right]\stackrel{!}{<}0$$

(20)

As it can be seen in Equation (21), the term fulfills Lyapunov stability criterion for any K_ISM > |h_max/B|.

$$\dot{V}=\frac{s}{2}\left[h-{\mathit{BK}}_{\mathit{ISM}}\mathrm{sign}\left(s\right)\right]\stackrel{!}{<}0$$

(21)

Figure 7 shows the comparison between both strategies for performing an emergency braking manoeuver on a wet surface. Compared with the PI control, the ISM control shows much faster convergence towards the reference values. Moreover, the remaining error is lower. In addition, the figure proves that the IWMs show a higher dynamic for control.

5. Real-Time Integration and Experimental Studies

The presented investigations were done with subsystem models, validated from the industrial partners, since the real hardware was not available on schedule due to the COVID-19 pandemic.

The vehicle dynamics’ model of the target sport utility vehicle (SUV) was created and experimentally validated in former investigations with CarMaker environment from IPG Automotive GmbH in collaboration with the related OEM. It used 255/50 R20 tires.

As there are different controller functionalities and even because the scenarios vary in their circumstances, some key performance indicators (KPIs (see Equations (22)–(24)) were needed for an optimal comparison.

(A) 

Braking distance (safety criterion)

This parameter was directly extracted from IPG CarMaker environment.

(B) 

Root-mean square error (RMSE) of the vehicle yaw rate (stability criterion)

$${\mathit{RMSE}}_{\dot{\psi }}=\sqrt{\frac{1}{N}{\displaystyle \sum }_{k=1}^N{{(\dot{\psi }}_k-\overline{\dot{\psi }})}^2}$$

(22)

(C) 

Root-mean square error of the vehicle longitudinal jerk (comfort criterion)

$${\mathit{RMSE}}_{\stackrel{⃛}{x}}=\sqrt{\frac{1}{N}{\displaystyle \sum }_{k=1}^N{{(\stackrel{⃛}{x}}_k-\overline{\stackrel{⃛}{x}})}^2}$$

(23)

(D) 

Normalized integral of the absolute value of the control action (IACA)

$${\mathit{IACA}}_{\mathit{WSC}}={{\displaystyle \int }}_{t_0}^{t_N}\left[\frac{1}{4}\mathrm{sum}(\left|T_{\mathit{WSC}}{}^{ij}\right|)-{\overline{T}}_{\mathit{WSC}}{}^{ij}\right]\mathit{dt}$$

(24)

T_WSC stands for the control effort of both the IWMs’ and the brake-by-wire-system’s actuators on each corner. With the IACA parameter, a statement about the actuator wear is possible, but any specification of a critical value was not the aim of the authors in this study and is therefore be left to the scope of other publications.

To demonstrate the advantages of the continuous approach, a rule-based controller, adopted from [29], was additionally implemented. The background is, that most common ABS algorithms use a rule-based control approach. This rule-based and the two other described approaches were compared against the case without any wheel slip control.

Table 2. Test case matrix.

Test-ID	Friction Coefficient µr (–)	Pedal Application Speed dsPed/dt (mm/s)	Initial Vehicle Speed vinit (km/h)
Test 1	0.4 | 0.4	200	40
Test 2		50
Test 3		200	60
Test 4		50
Test 5	0.9 | 0.9	200	60
Test 6			120
Test 7	0.4 | 0.9		60
Test 8			90
Test 9	patch		120

includes all the different test cases that were part of the simulative studies in IPG CarMaker under real-time conditions. Every described Test-ID was run with rule-based, PI and ISM control and compared to the performance without wheel slip control system. Moreover, the tests were done with and without torque blending control, providing 72 simulation sets in total.

Figure 8 and Figure 9 show the results of the studies. All the listed test cases were performed with a pedal travel speed of 200 mm/s, excluding test cases 2 and 4, which were performed with 50 mm/s to investigate whether this had any influence.

First, the results for high and low µ conditions are not surprising and match the expectations for performance with and without torque blending. In particular, it is worth noticing that the continuous approaches reduced the braking distance by over 13% compared with deactivated wheel slip control. This effect was strengthened at higher initial vehicle speeds, as shown for test case 5 (v_init = 120 km/h).

Naturally, the improvements were also higher with faster pedal application speed. Hence, in cases in which no emergency braking is necessary, lower pedal application speed can nevertheless bring some improvements, e.g., with regard to ride comfort since the longitudinal jerk was significantly reduced without major safety or stability compromise. In the investigations, the comfort improvements between test cases with different pedal application speeds amounted to ~39% for the continuous approaches, while the braking distance and yaw rate variations were below 1%. For rule-based control, the longitudinal jerk amount was nearly three times higher than for the continuous approaches. This resulted from the missing modulation of the brake calipers’ clamping forces using rule-based control, which makes it jerkier and remarkably uncomfortable. Moreover, the deactivated WSC seemed to be best with regard to non-jerky brake performance but, as a consequence of the locked wheels, safety was not properly ensured, especially for the lateral dynamics.

Regarding vehicle stability, test cases 1 to 6 were quite uninteresting since a homogeneous surface with a constant friction coefficient was assumed. The results on underground surfaces with inhomogeneous friction conditions (µ-split, test cases 7–8) or even randomly distributed patches with different friction coefficients (test case 9) were more interesting, as the vehicle tended to turn around its COG because of the emerging yaw moment produced by different longitudinal forces on the left and right wheels.

Therefore, the braking distance became less interesting for those test cases, but the stability criterion stepped into the foreground. As described at the beginning of this section, deactivated control seemed to be advantageous in ride comfort, but it failed in terms of vehicle stability as the blocked wheels did not guarantee a sufficient transmission of lateral forces. It can be seen in this case that the continuous approaches are showing similar performances, while there are significant improvements with −93.6% (case 7)/97.1% (case 8) for PI and −54.6% (case 7)/−97.1% (case 8) for ISM compared with the deactivated control. Compared to the rule-based control, which already showed much better performance than deactivated WSC, the continuous approaches showed noticeable improvements of −46.3% (case 7)/−51% (case 8) for PI control and −46.5% (case 7)/52.3% (case 8) for ISM. It becomes clearthen, that there was no scenario with higher improvements through continuous control than in the braking manoeuver from 60 km/h to standstill on µ-split road (test case 8). Additionally to the stability improvements, there was also a reduction of the longitudinal jerk by ~30%.

For test case 9, the improvements were −62.6%/−78.6 (PI) against the deactivated control and rule-based control, while the ISM reduced the yaw rate by ~31% for both.

As specified in Table 2, the second half of the experiments was done with the activated toque blending algorithm described in Section 4.2. The blending factor was set to α = 1 (serial phasing) in accordance with the original blending strategy of the target vehicle. Observing Figure 9, it can be stated that the behavior for test cases 1 to 4 was comparable to that for the cases without blended torque, with some minor improvements in vehicle safety and stability criteria. To avoid misunderstandings, we should note that active torque blending can remarkably influence vehicle safety too, but in the case of emergency braking maneuver, the brake torque should be applied fully to the EHB on the front and the EMB on the rear axle. This is given by [28]. There is only a short time slot for using the electric machines, given by the duration of the switching of the blending factor, see Figure A3.

Nevertheless, it is clear that the longitudinal jerk was reduced by up to >20% with PI and ~15% with ISM by using the blending. This is consistent with the expectation, since the negative influences during ABS braking can occur due to brake force fluctuations. If so, the deceleration signal oscillates. When using the electric machines, those fluctuations do not exist, which was reflected in the specified reductions of vehicle longitudinal jerk.

Again, the most interesting scenarios were test cases 7 and 8 with a µ-split road. As before, the stability criterion prevailed as the KPI of braking distance. The yaw rate could be decreased by 40.2% (test case 7)/46.6% (test case 8) for PI and 42.8% (test case 7)/48.6% (test case 8) for ISM in those scenarios, compared with the rule-based approach.

Finally, PI and ISM control seemed to be differently effective with regard to blending status. The ISM controller mostly provided better results or improvements than the PI control in comparison with the rule-based variant. In the simulation sets with activated torque blending, the results were the other way round. This may relate to the controller tuning, but is ignored at this point since the deviations are not significant. Further investigations on that point could be part of future publications.

6. Conclusions

This paper described the set-up, implementation, and real-time testing of an integrated braking control, providing safety systems, like wheel slip control, and enhanced functionality, such as torque blending as well. For wheel slip regulation, a benchmarking test comparing continuous control strategies with a classical rule-based approach was performed.

During these tests, the following results have been achieved:

i

The developed observers were able to detect variations in vehicle mass and road slope for internal compensation properly.

ii

The enhanced blending functionality was able to consider limitation factors in order to switch between torque blending and full electric/friction braking.

iii

Due to their higher dynamics, the usage of electric in-wheel motors showed advantages for wheel slip control compared with the rule-based control, especially in terms of vehicle stability and ride comfort.

iv

The experimental investigations showed the PI and ISM robustness for variation of the tire-road-friction coefficient and different initial vehicle speeds.

v

On a µ-split surface, the continuous control improved vehicle stability by up to >97%, which is nearly 10% more than the rule-based approach.

vi

PI and ISM control showed a significant reduction of vehicle longitudinal jerk of ~30%, while the rule-based improvement was only about 22%.

Hence, it is clear that there is a conflict between the criteria of safety, stability, and comfort, that has to be solved during the development and tuning of such controllers in order to achieve a satisfactory result. The results achieved in this investigation reflect the best compromise of all these parameters, taking into account the tunable controller gains and limitations through the methodology. Moreover, the performance of these active safety systems strongly depends on the tire road interaction. For simulative studies, an entirely validated and well-parameterized tire and contact model is needed to show realistic behavior. Since the investigations did not focus on these models, a standard Magic Formula model was used.

Nevertheless, the results showed the very high potential of continuous wheel slip control for automotive applications in general and the presented case study shows the feasibility for modern battery electric vehicles with hybrid brake systems containing EHB and EMB actuators and in-wheel propulsion in particular. The methodology presented is applicable to future drivetrains and components, that differ from those of the current study through the implementation of minor changes.