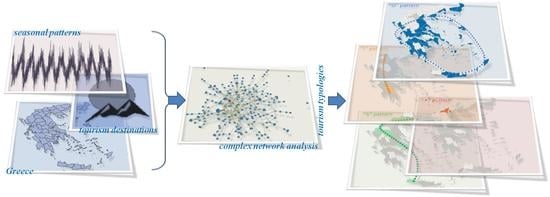
Detecting Tourism Typologies of Regional Destinations Based on Their Spatio-Temporal and Socioeconomic Performance: A Correlation-Based Complex Network Approach for the Case of Greece
Abstract
:1. Introduction
2. Methodology and Data
3. Results and Discussion
3.1. Data Visualization
3.2. Correlation Analysis
3.3. Classification of Seasonality Patterns Based on Community Detection
3.4. Socio-Economic Determination of the Modularity Seasonal Groups
4. Further Analysis and Overall Assessment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| TOURISM SEASONALITY | |||||||
|---|---|---|---|---|---|---|---|
| A. CONCEPTUALIZATION | B. MODELING | C. IMPLEMENTATION | |||||
| A1. Definition | A2. Space of Embedding | B1. Variable Complexity | B2. Data | B3. Attribute/Aspect | B4. Models | B5. Approach | C1. Geographical Scale |
| 1. Tourism Demand [1,6,9,12,14,15,16,18,20,21,22,28,30,31,32,34,37,38,39,40,41,44,45], | 1. Socioeconomic [1,9,12,15,16,17,18,20,21,22,28,32,37,41,42,44,45] | 1. Uni-variable (one attribute) [6,14,32,33,40,41,43,45] | 1. Visitors [6,22,30,31,34,39] | 1. Concentration [9,39,40,42,45] | 1. Indicators [6,12,14,18,19,22,28,29,30,31,32,34,35,36,38,39,40,41,45] | 1. Single discipline [6,12,13,14,29,30,31,32,35,38,39,40,41,42,43] | |
| 2. Multivariable (many attributes) [9,15,16,20,21,22,28,31,34] | 2. Arrivals [13,15,16,32,33,34,41,42] | 2. Synergy [5] | 2. Measures/metrics [9,14,21,31,36,40,43] | 2.Multidisciplinary [9,15,16,17,21,22,28,33,34,44,45] | |||
| 3. Overnight-stays [9,12,14,17,18,29,31,32,36,38,40,45] | 3. Traditions [4,6,12,18] | 3. Econometric [15,17,21,22,44,45] | |||||
| 4. Income [16]. | 4. Tourism-capacity [42]. | ||||||
| 5. Occupancy [12,16,17,18,31,35] | 5. Competitiveness [22,23,32,42] | ||||||
| 6. Number of trips [28] | 6. Attractiveness [19,29,44] | ||||||
| 7. Staff [31,45] | 7. Economic structure/configuration [15,44,45] | ||||||
| 8. Prices [31] | 8. Type of tourism product [6,12,17,18,28,30,31,32,35,37,39,40,44] | ||||||
| 2. Time References [1,6,9,11,12,15,17,20,27,29,33,35,40,43,45] | 2. Temporal (time dimension) [9,13,18,29,33,34,35,38,39,41] | 1. Uni-variable [13,29,35,38,39] | 9. Daily [34,35,41] | 9. Scale [4,5,17,27,36,40] | 4. Measures/metrics [5,13,35,36] | 1. Single discipline [6,12,29,35,38,39,40,43] | |
| 10. Weekly [34,41,43] | 10.Variability [4,5,15,28,35,36,41] | 5. Time-series [9,13,29,33,35] | |||||
| 11. Monthly [6,9,12,13,15,16,18,28,29,30,31,33,35,38,39,40,41,43,45] | 11. Periodicity [4,13,15,35,36,38,40,41] | 6. TALC [42,49]. | 2. Multidisciplinary [9,15,17,33,45] | ||||
| 12.Annual [14,19,21,35,40] | 12. Cyclical performance [9,14,29,35,36] | 7. Pattern recognition [9,29,35,36,38,39] | |||||
| 3. Spatial References [6,9,12,14,15,16,17,18,19,20,21,25,28,30,32,34,37,39,40,42,43] | 3. Geography (spatial dimension) [9,12,14,15,16,17,18,19,29,31,34,40,42,43] | 1. Uni-variable (one destination) [12,18,30,32,33,34,35,41] | 13. Location [12,13,18,21,30,32,34,35,41,42] | 13. Geographical scale [6,9,19,28,42,44] | 7. Pattern recognition [12,14,18,42] | 1. Single discipline [6,12,14,29,30,39,40,42,43] | 1. Local [13,17,21,30,32,34,35,41,42] |
| 2. Multivariable (many destinations) [6,9,14,15,16,17,19,28,34,36,38,39,40,43,44,45] | 14. Destination [9,14,15,16,17,22,28,31,33,34,36,38,41,42,43,44,45] | 14. Geomorphology [9,16] | 8. Classification [6,9,14,19,22,44] | 2. Multidisciplinary [9,15,16,17,21,28,34] | 2.Urban [34] | ||
| 3. Climate [15,16],19] | 3. Regional [6,9,16,19,28,29,31,34,38,39,40,43,44,45] | ||||||
| 15. Accessibility [16,30] | 4. National [12,18,22,33,34,40] | ||||||
| 5. International [14,15,36] | |||||||
| Prefecture | Variable Code | Prefecture | Variable Code | Prefecture | Variable Code | Prefecture | Variable Code |
|---|---|---|---|---|---|---|---|
| ACHAIA | 34 | EVROS | 3 | KEFALONIA | 32 | PIERIA | 10 |
| AITOLOAKARNANIA | 35 | EVRYTANIA | 28 | KERKYRA | 30 | PREVEZA | 20 |
| ARGOLIDA | 38 | FLORINA | 16 | KILKIS | 8 | RETHYMNO | 50 |
| ARKADIA | 37 | FOKIDA | 29 | KORINTHIA | 39 | RODOPI | 1 |
| ARTA | 18 | FTHIOTIDA | 25 | KOZANI | 13 | SAMOS | 44 |
| ATTIKI | 42 | GREVENA | 14 | LAKONIA | 40 | SERRES | 11 |
| CHALKIDIKI | 12 | HELEIA | 36 | LARISSA | 21 | THESPOTIA | 19 |
| CHANIA | 51 | HERAKLION | 48 | LASITHI | 49 | THESSALONIKI | 6 |
| CHIOS | 45 | HMATHIA | 7 | LEFKADA | 33 | TRIKALA | 24 |
| CYCLADES | 46 | IOANNINA | 17 | LESVOS | 43 | VIOTIA | 26 |
| DODECANESE | 47 | KARDITSA | 22 | MAGNESIA | 23 | XANTHI | 5 |
| DRAMA | 2 | KASTORIA | 15 | MESSENIA | 41 | ZAKEENTHOS | 31 |
| EVIA | 27 | KAVALA | 4 | PELLA | 9 |
| Code | Variable’s Symbol | Description | Source |
|---|---|---|---|
| SEG.1 | LAT | Latitude, defined by the geographical center of the prefecture. | [63] |
| SEG.2 | LONG | Longitude, defined by the geographical center of the prefecture. | [63] |
| SEG.3 | RSI | The Relative Seasonality Index of the prefectures’ seasonality patterns | [9] |
| SEG.4 | GINI | The Gini coefficient of the prefectures’ seasonality patterns | [9] |
| SEG.5 | ROAD DENSITY | The road density (road length/area) of each prefecture (measured in km/km2). | [64,65,66,67,68] |
| SEG.6 | ROAD LENGTH | The road length of each prefecture (measured in km). | [64,65,66,67,68] |
| SEG.7 | COASTAL | Dummy variable capturing coastal configuration (1 = coastal perfectures; 0 = non-coastal perfectures). | [67] |
| SEG.8 | ISLAND | Dummy variable capturing island configuration. | [59] |
| SEG.9 | INLAND | Dummy variable capturing inland configuration. | [59] |
| SEG.10 | RAIL | The length of the rail network. | [48,68] |
| SEG.11 | PORTS | The number of ports. | [59,68] |
| SEG.12 | AIRPORTS | The number of airports. | [59,68] |
| SEG.13 | AREA | The geographical area (measured in km2). | [59] |
| SEG.14 | POP | The regional population (2011 national census). | [65] |
| SEG.15 | URB | The urbanization level (i.e., the proportion of the capital city’s population to the regional population). | [65] |
| SEG.16 | GDP | Gross Domestic Product. | [65] |
| SEG.17 | Human Capital | Defined by the proportion of labor-force (i.e., population between 18 and 65 years old) to the total population. | [1] |
| SEG.18 | ASEC | The specialization (% of the GDP) in the primary (A) sector. | [66,69] |
| SEG.19 | BSEC | The specialization (% of the GDP) in the secondary (B) sector. | [66,69] |
| SEG.20 | CSEC | The specialization (% of the GDP) in the tertiary (C) sector. | [66,69] |
| SEG.21 | TOURISM GDP | The specialization (% of the GDP) in the tourism sector. | [66] |
| SEG.22 | TILLING LAND | The proportion of the tilling-land areas to the total regional area. | [67] |
| SEG.23 | FORESTS | The proportion of forest-areas to the total regional area. | [67] |
| SEG.24 | INLAND WATERS | The proportion of the inland-water-areas to the total regional area. | [67] |
| SEG.25 | INDUSTRIAL AREA | The proportion of the industrial-areas to the total regional area. | [67,69] |
| SEG.26 | LAND AREA | The proportion of (non-mountainous) land-areas to the total regional area. | [67] |
| SEG.27 | SEMI MOUNTAIN AREA | The proportion of the semi-mountain areas to the total regional area. | [67] |
| SEG.28 | MOUNTAIN AREA | The proportion of the mountain-areas to the total regional area. | [67] |
| SEG.29 | MOUNT ACTIVITIES | The number of mountain-activities (e.g., walking paths, mount sports, climb fields). | [67] |
| SEG.30 | CLIMB FIELDS | The number of climb-fields. | [67] |
| SEG.31 | MOUNT ROUTES | The number of mountain-routes. | [67] |
| SEG.32 | RAFTING POINTS | The number of rafting-points. | [67] |
| SEG.33 | CANYONING POINTS | The number of canyoning-points. | [67] |
| SEG.34 | SKI CENTERS | The number ski-centers. | [67] |
| SEG.35 | SKI ROUTES LENGTH | The length of the ski-routes (measured in km). | [67] |
| SEG.36 | RESTAURANTS | The number of restaurants. | [67] |
| SEG.37 | NATURA AREA | The geographical area of the Natura parks (i.e., environmentally protected areas). | [67] |
| SEG.38 | WOODLANDS PARKS | The number of woodland-parks. | [67] |
| SEG.39 | HOTELS | The number of hotels. | [66] |
| SEG.40 | CAMPING | The number of camping sites. | [66] |
| SEG.41 | BLUE FLAG | The number of beaches that are granted a blue flag. | [66] |
| SEG.42 | BEACHES | The number of organized beaches. | [66] |
| SEG.43 | ANC MONUMENTS | The number of ancient monument sites. | [66] |
| SEG.44 | UNESCO MONUMENTS | The number of UNESCO monument sites. | [66] |
| SEG.45 | HOTEL BEDS | The number of hotel beds (bed capacity). | [66] |
| SEG.46 | ROOMS | The number of rooms to let (non-hotel accommodation). | [66] |
| SEG.47 | ROOMS BEDS | The number of rooms’ beds (non-hotel accommodation capacity). | [66] |
| SEG.48 | ACCOMMODATION BEDS | The number of other types of accommodation beds. | [66] |
| SEG.49 | CULTURAL RESOURCES | The number of cultural-resources sites. | [67] |
| SEG.50 | BEACHES LENGTH | The length of beaches. | [67] |
| SEG.51 | SAND BEACHES LENGTH | The length of sand beaches. | [67] |
| MODULARITY GROUPS | |||||
|---|---|---|---|---|---|
| Variable Code | Variable Name | (0,0,1) | (1,1,0) | (1,1,1) | (2,2,0) |
| GEOGRAPHIC | |||||
| SEG1 | LAT | MAX | MAX | MIN | |
| SEG2 | LONG | MAX | MIN | MAX | |
| SEG3 | COASTAL | MIN | MIN | MAX | |
| SEG4 | ISLAND | MIN | MIN | MAX | |
| SEG5 | INLAND | MIN | MAX | ||
| SEG6 | AREA | MIN | MAX | MIN | |
| SEG7 | TILLING LAND | MAX | MIN | MIN | |
| SEG8 | FORESTS | MAX | MIN | ||
| SEG9 | INLAND WATERS | MIN | MAX | MIN | |
| SEG10 | LAND AREA | MAX | MIN | ||
| SEG11 | SEMI MOUNTAIN AREA | MIN | MAX | MIN | MIN |
| SEG12 | MOUNTAIN AREA | MAX | MIN | ||
| SEASONALITY | |||||
| SEG13 | RSI | MIN | MIN | MAX | |
| SEG14 | GINI | MIN | MIN | MIN | MAX |
| TRANSPORT | |||||
| SEG15 | ROAD DENSITY | MIN | MAX | ||
| SEG16 | ROAD LENGTH | ||||
| SEG17 | RAIL | MAX | MIN | ||
| SEG18 | PORTS | MIN | MIN | MIN | MAX |
| SEG19 | AIRPORTS | MAX | MIN | ||
| DEMOGRAPHIC | |||||
| SEG20 | POP | MAX | MIN | ||
| SEG21 | URB | MAX | MIN | MAX | MAX |
| SEG22 | HUMAN CAPITAL | MAX | MIN | ||
| PRODUCTIVITY | |||||
| SEG23 | GDP | MAX | MIN | ||
| SEG24 | ASEC | MIN | MAX | ||
| SEG25 | BSEC | MIN | MAX | MIN | MIN |
| SEG26 | CSEC | MIN | MAX | MAX | |
| SEG27 | TOURISM GDP | MAX | MIN | ||
| SEG28 | INDUSTRIAL AREA | MIN | MAX | MIN | MIN |
| TOURISM | |||||
| SEG29 | HOTELS | MIN | MIN | MAX | |
| SEG30 | HOTEL BEDS | MIN | MIN | MAX | |
| SEG31 | ROOMS | MIN | MIN | MAX | |
| SEG32 | ROOMS BEDS | MIN | MIN | MAX | |
| SEG33 | ACCOMMODATION BEDS | MIN | MIN | MAX | |
| SEG34 | CAMPING | MIN | MIN | MIN | MAX |
| SEG35 | RESTAURANTS | MIN | MIN | MAX | |
| SEG36 | MOUNT ACTIVITIES | MAX | MIN | MIN | |
| SEG37 | CLIMB FIELDS | MAX | MIN | MAX | MAX |
| SEG38 | MOUNT ROUTES | MAX | MIN | MIN | |
| SEG39 | RAFTING POINTS | ||||
| SEG40 | CANYONING POINTS | MIN | MAX | ||
| SEG41 | SKI CENTERS | MAX | MIN | MAX | MIN |
| SEG42 | SKI ROUTES LENGTH | MAX | MIN | ||
| ENVIRONMENTAL | |||||
| SEG43 | NATURA AREA | MAX | MIN | MAX | MAX |
| SEG44 | WOODLANDS PARKS | MAX | MIN | ||
| SEG45 | BLUE FLAG BEACHES | MIN | MIN | MAX | |
| SEG46 | BEACHES | MIN | MIN | MIN | MAX |
| SEG47 | BEACHES LENGTH | MIN | MIN | MIN | MAX |
| SEG48 | SAND BEACHES LENGTH | MIN | MIN | MIN | MAX |
| CULTURAL | |||||
| SEG49 | ANC MONUMENTS | MIN | MAX | ||
| SEG50 | UNESCO MONUMENTS | MIN | MIN | MAX | |
| SEG51 | CULTURAL RESOURCES | MIN | MAX | ||
References
- Polyzos, S. Regional Development; Kritiki: Athens, Greece, 2019; ISBN 9789602187302. [Google Scholar]
- Mastronardi, L.; Cavallo, A. The Spatial Dimension of Income Inequality: An Analysis at Municipal Level. Sustainability 2020, 12, 1622. [Google Scholar] [CrossRef] [Green Version]
- Vo, D.H.; Nguyen, T.C.; Tran, N.P.; Vo, A.T. What Factors Affect Income Inequality and Economic Growth in Middle-Income Countries? J. Risk Financial Manag. 2019, 12, 40. [Google Scholar] [CrossRef] [Green Version]
- Charles-Edwards, E.; Bell, M. Seasonal Flux in Australia’s Population Geography: Linking Space and Time. Popul. Space Place 2013, 21, 103–123. [Google Scholar] [CrossRef]
- Romão, J.; Saito, H. A spatial analysis on the determinants of tourism performance in Japanese Prefectures. Asia-Pac. J. Reg. Sci. 2017, 1, 243–264. [Google Scholar] [CrossRef] [Green Version]
- Batista e Silva, F.; Kavalov, B.; Lavalle, C. Socio-Economic Regional Microscope Series—Territorial Patterns of Tourism Inten-Sity and Seasonality in the EU; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar] [CrossRef]
- Ulbrich, P.; de Albuquerque, J.P.; Coaffee, J. The Impact of Urban Inequalities on Monitoring Progress towards the Sustainable Development Goals: Methodological Considerations. ISPRS Int. J. Geo-Inf. 2018, 8, 6. [Google Scholar] [CrossRef] [Green Version]
- Băndoi, A.; Jianu, E.; Enescu, M.; Axinte, G.; Tudor, S.; Firoiu, D. The Relationship between Development of Tourism, Quality of Life and Sustainable Performance in EU Countries. Sustainability 2020, 12, 1628. [Google Scholar] [CrossRef] [Green Version]
- Tsiotas, D.; Krabokoukis, T.; Polyzos, S. Detecting Interregional patterns in tourism-seasonality of Greece: A principal components analysis approach. Reg. Sci. Inq. 2020, 12, 91–112. [Google Scholar]
- Krabokoukis, T.; Polyzos, S. An Investigation of Factors Determining the Tourism Attractiveness of Greece’s Prefectures. J. Knowl. Econ. 2020. [Google Scholar] [CrossRef]
- Saarinen, J.; Rogerson, C.M.; Hall, C.M. Geographies of tourism development and planning. Tour. Geogr. 2017, 19, 307–317. [Google Scholar] [CrossRef]
- Butler, R.W. Seasonality in tourism: Issues and implications. In Tourism: The State of the Art; Seaton, A., Ed.; Wiley: Chichester, UK, 1994; ISBN 978-0471950929. [Google Scholar]
- Gil-Alana, L.A. International Arrivals in the Canary Islands: Persistence, Long Memory, Seasonality and other Implicit Dynamics. Tour. Econ. 2010, 16, 287–302. [Google Scholar] [CrossRef]
- Ferrante, M.; Magno, G.L.L.; De Cantis, S. Measuring tourism seasonality across European countries. Tour. Manag. 2018, 68, 220–235. [Google Scholar] [CrossRef]
- Duro, J.A.; Turrión-Prats, J. Tourism seasonality worldwide. Tour. Manag. Perspect. 2019, 31, 38–53. [Google Scholar] [CrossRef] [Green Version]
- Sæþórsdóttir, A.D.; Hall, C.M.; Stefánsson, Þ. Senses by Seasons: Tourists’ Perceptions Depending on Seasonality in Popular Nature Destinations in Iceland. Sustainability 2019, 11, 3059. [Google Scholar] [CrossRef] [Green Version]
- Corluka, G.; Mikinac, K.; Milenkovska, A. Classification of tourist season in coastal tourism. UTMS J. Econ. 2016, 7, 71–83. [Google Scholar]
- Butler, R.W. Seasonality in Tourism: Issues and Implication. In Seasonality in Tourism; Baum, T., Lundtorp, S., Eds.; Elsevier Ltd.: Oxford, UK, 2001; ISBN 9780080436746. [Google Scholar]
- Fang, Y.; Yin, J. National Assessment of Climate Resources for Tourism Seasonality in China Using the Tourism Climate Index. Atmosphere 2015, 6, 183–194. [Google Scholar] [CrossRef] [Green Version]
- De Almeida, A.L.; Kastenholz, E. Towards a Theoretical Model of Seasonal Tourist Consumption Behaviour. Tour. Plan. Dev. 2018, 16, 533–555. [Google Scholar] [CrossRef]
- Choe, Y.; Kim, H.; Joun, H.-J. Differences in Tourist Behaviors across the Seasons: The Case of Northern Indiana. Sustainability 2019, 11, 4351. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Li, Y.; Parkpian, P. Inbound tourism in Thailand: Market form and scale differentiation in ASEAN source countries. Tour. Manag. 2018, 64, 22–36. [Google Scholar] [CrossRef]
- Gómez-Vega, M.; Picazo-Tadeo, A.J. Ranking world tourist destinations with a composite indicator of competitiveness: To weigh or not to weigh? Tour. Manag. 2019, 72, 281–291. [Google Scholar] [CrossRef]
- Niavis, S.; Tsiotas, D. Decomposing the price of the cruise product into tourism and transport attributes: Evidence from the Mediterranean market. Tour. Manag. 2018, 67, 98–110. [Google Scholar] [CrossRef]
- Tsiotas, D.; Niavis, S.; Sdrolias, L. Operational and geographical dynamics of ports in the topology of cruise networks: The case of Mediterranean. J. Transp. Geogr. 2018, 72, 23–35. [Google Scholar] [CrossRef]
- Niavis, S.; Tsiotas, D. Assessing the tourism performance of the Mediterranean coastal destinations: A combined efficiency and effectiveness approach. J. Destin. Mark. Manag. 2019, 14, 100379. [Google Scholar] [CrossRef]
- Romão, J.; Guerreiro, J.; Rodrigues, P.M.M. Territory and Sustainable Tourism Development: A Space-Time Analysis on European Regions. Region 2017, 4, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Fernández-Morales, A.; Cisneros-Martínez, J.D.; McCabe, S. Seasonal concentration of tourism demand: Decomposition analysis and marketing implications. Tour. Manag. 2016, 56, 172–190. [Google Scholar] [CrossRef]
- Cuccia, T.; Rizzo, I. Tourism seasonality in cultural destinations: Empirical evidence from Sicily. Tour. Manag. 2011, 32, 589–595. [Google Scholar] [CrossRef]
- Lundtorp, S.; Rassing, C.R.; Wanhill, S. The off-Season is ‘No Season’: The Case of the Danish Island of Bornholm. Tour. Econ. 1999, 5, 49–68. [Google Scholar] [CrossRef]
- Martín, J.M.M.; Fernández, J.A.S. Comprehensive evaluation of the tourism seasonality using a synthetic DP2 indicator. Tour. Geogr. 2019, 21, 284–305. [Google Scholar] [CrossRef]
- Andriotis, K. Seasonality in Crete: Problem or a Way of Life? Tour. Econ. 2005, 11, 207–224. [Google Scholar] [CrossRef]
- Assaf, A.G.; Barros, C.P.; Gil-Alana, L.A. Persistence in the Short- and Long-Term Tourist Arrivals to Australia. J. Travel Res. 2010, 50, 213–229. [Google Scholar] [CrossRef]
- Þórhallsdóttir, G.; Ólafsson, R. A method to analyse seasonality in the distribution of tourists in Iceland. J. Outdoor Recreat. Tour. 2017, 19, 17–24. [Google Scholar] [CrossRef]
- De Cantis, S.; Ferrante, M.; Vaccina, F. Seasonal Pattern and Amplitude—A Logical Framework to Analyse Seasonality in Tourism: An Application to Bed Occupancy in Sicilian Hotels. Tour. Econ. 2011, 17, 655–675. [Google Scholar] [CrossRef]
- Magno, G.L.L.; Ferrante, M.; De Cantis, S. A new index for measuring seasonality: A transportation cost approach. Math. Soc. Sci. 2017, 88, 55–65. [Google Scholar] [CrossRef]
- Koenig-Lewis, N.; Bischoff, E.E. Seasonality research: The state of the art. Int. J. Tour. Res. 2005, 7, 201–219. [Google Scholar] [CrossRef]
- Fernández-Morales, A. Decomposing seasonal concentration. Ann. Tour. Res. 2003, 30, 942–956. [Google Scholar] [CrossRef]
- Cisneros-Martínez, J.D.; Fernández-Morales, A. Cultural tourism as tourist segment for reducing seasonality in a coastal area: The case study of Andalusia. Curr. Issues Tour. 2013, 18, 765–784. [Google Scholar] [CrossRef]
- Duro, J.A. Seasonality of hotel demand in the main Spanish provinces: Measurements and decomposition exercises. Tour. Manag. 2016, 52, 52–63. [Google Scholar] [CrossRef] [Green Version]
- Rosselló, J.; Sansó, A. Yearly, monthly and weekly seasonality of tourism demand: A decomposition analysis. Tour. Manag. 2017, 60, 379–389. [Google Scholar] [CrossRef]
- Terkenli, T.S. Human Activity in Landscape Seasonality: The Case of Tourism in Crete. Landsc. Res. 2005, 30, 221–239. [Google Scholar] [CrossRef]
- Ahas, R.; Aasa, A.; Mark, Ü.; Pae, T.; Kull, A. Seasonal tourism spaces in Estonia: Case study with mobile positioning data. Tour. Manag. 2007, 28, 898–910. [Google Scholar] [CrossRef]
- Connell, J.; Page, S.J.; Meyer, D. Visitor attractions and events: Responding to seasonality. Tour. Manag. 2015, 46, 283–298. [Google Scholar] [CrossRef] [Green Version]
- Cisneros-Martínez, J.D.; McCabe, S.; Morales, A.F. The contribution of social tourism to sustainable tourism: A case study of seasonally adjusted programmes in Spain. J. Sustain. Tour. 2018, 26, 85–107. [Google Scholar] [CrossRef]
- World Bank. World Development Indicators: Travel and Tourism. 2020. Available online: http://wdi.worldbank.org/table/6.14 (accessed on 18 December 2020).
- INSETE. The Contribution of Tourism to the Greek Economy. 2020. Available online: https://insete.gr/bi/ (accessed on 18 December 2020).
- Tsiotas, D. The imprint of tourism on the topology of maritime networks: Evidence from Greece. Anatolia 2016, 28, 52–68. [Google Scholar] [CrossRef]
- Polyzos, S.; Tsiotas, D.; Kantlis, A. Determining the Tourism Developmental Dynamics of the Greek Regions, by using TALC Theory, Tourismos: An International Multidisciplinary. J. Tour. 2013, 8, 159–178. [Google Scholar]
- Kalantzi, O.; Tsiotas, D.; Polyzos, S. The contribution of tourism in national economies: Evidence of Greece. EJBSS 2016, 5, 41–64. [Google Scholar]
- Barabási, A.-L. Network science. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120375. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Networks: An Introduction; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Boccaletti, S.; Bianconi, G.; Criado, R.; del Genio, C.; Gómez-Gardeñes, J.; Romance, M.; Sendiña-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef] [Green Version]
- Tsiotas, D. Detecting different topologies immanent in scale-free networks with the same degree distribution. Proc. Natl. Acad. Sci. USA 2019, 116, 6701–6706. [Google Scholar] [CrossRef] [Green Version]
- Baggio, R.; Valeri, M. Network science and sustainable performance of family businesses in tourism. J. Fam. Bus. Manag. 2020. [Google Scholar] [CrossRef]
- Valeri, M.; Baggio, R. Italian tourism intermediaries: A social network analysis exploration. Curr. Issues Tour. 2020, 1–14. [Google Scholar] [CrossRef]
- Valeri, M.; Baggio, R. Social network analysis: Organizational implications in tourism management. Int. J. Organ. Anal. 2020. [Google Scholar] [CrossRef]
- Tsiotas, D.; Tselios, V. Understanding the uneven spread of COVID-19 in the context of the global interconnected economy. arXiv 2021, arXiv:2101.11036. [Google Scholar]
- Hellenic Statistical Authority—ELSTAT 2019a. Number of Monthly Overnight-Stays in the Greek Prefectures for the Period 1998–2018. Available online: www.statistics.gr (accessed on 18 December 2020).
- Walpole, R.E.; Myers, R.H.; Myers, S.L.; Ye, K. Probability & Statistics for Engineers & Scientists, 9th ed.; Prentice Hall Publications: New York, NY, USA, 2012; ISBN 9780321629111. [Google Scholar]
- Fortunato, S. Community detection in graphs. Phys. Rep. 2010, 486, 75–174. [Google Scholar] [CrossRef] [Green Version]
- Blondel, V.D.; Guillaume, J.-L.; Lambiotte, R.; Lefebvre, E. Fast unfolding of communities in large networks. J. Stat. Mech. Theory Exp. 2008, 2008, P10008. [Google Scholar] [CrossRef] [Green Version]
- Google Maps. Google Mapping Services. 2020. Available online: www.google.gr/maps?hl=el (accessed on 18 December 2020).
- Tsiotas, D. Links between network topology and socio-economic framework of railway transport: Evidence from Greece. J. Eng. Sci. Technol. Rev. 2017, 10, 175–187. [Google Scholar] [CrossRef]
- Hellenic Statistical Authority—ELSTAT. Population and Social Conditions. 2019. Available online: https://www.statistics.gr/el/statistics/pop (accessed on 3 June 2020).
- Hellenic Statistical Authority—ELSTAT. Economy, Indices. 2019. Available online: https://www.statistics.gr/el/statistics/eco (accessed on 3 June 2020).
- Hellenic Statistical Authority—ELSTAT. Environment and Energy. 2019. Available online: https://www.statistics.gr/el/statistics/env (accessed on 3 June 2020).
- Polyzos, S.; Tsiotas, D. The contribution of transport infrastructures to the economic and regional development. Theor. Empir. Res. Urban Manag. 2020, 15, 5–23. [Google Scholar]
- Polyzos, S.; Tsiotas, D. Measuring structural changes of the Greek economy during the period of economic crisis. Manag. Res. Pract. 2020, 12, 5–24. [Google Scholar]










| Modularity Groups (Size) | Socio-Economic and Geographical Semiology | |
|---|---|---|
| MAX (a) | MIN (b) | |
| Group (0,0,1) (13 prefectures) | Northern and eastern location; urbanization; specialization in winter tourism activities; environmental wealth. | Area; seasonality; ports; camping; beaches. |
| Group (1,1,0) (1 prefecture) | Northern and west location; rich geomorphological configuration; mainland geomorphology; rich rail and airport configuration; high secondary sector specialization; high mountainous activities. | Coastal or island area; seasonality; poor road density and roads; low primary and tertiary sector specialization; low tourism profile; low environmental wealth, low cultural resources profile. |
| Group (1,1,1) (5 prefectures) | Mainland geomorphology; urbanization; high tertiary sector specialization; high environmental wealth. | Coastal or island area; poor geomorphological configuration; seasonality; poor ports and airports configuration; population and human capital; low income; low secondary sector specialization; low tourism profile; low beach environment; low cultural resources profile. |
| Group (2,2,0) (32 prefectures) | Southern and eastern location; coastal or island area, high seasonality; rich road density and ports configuration; high urbanization; high primary and tertiary sector specialization; high tourism profile; high environmental quality; high capacity of cultural resources. | Poor geomorphological configuration; poor rail configuration; low secondary sector specialization; low mountainous activities. |
| Modularity Group | |||||||||||||||||||
| Group Size | |||||||||||||||||||
| 32 | 13 | 5 | 1 | 32 | 13 | 5 | 1 | 32 | 13 | 5 | 1 | 32 | 13 | 5 | 1 | ||||
| Group Label | |||||||||||||||||||
| (2,2,0) | (0,0,1) | (1,1,1) | (1,1,0) | (2,2,0) | (0,0,1) | (1,1,1) | (1,1,0) | (2,2,0) | (0,0,1) | (1,1,1) | (1,1,0) | (2,2,0) | (0,0,1) | (1,1,1) | (1,1,0) | ||||
| Common Cases Between MOD and PCA Groups (intersection) | |||||||||||||||||||
| Group Size | Group Label | ◂Relevance to PCA Groups | Intersection Frequencies | ▴Relevance to MOD Groups | Differences in Relevance (MOD-PCA) | ||||||||||||||
| PCA Group | #1 (max filtering) | 38 | PCM#1 | 84.2% | 13.2% | 2.6% | 32 | 5 | 1 | 100% | 38.5% | 20.0% | 15.8% | 25.3% | 17.4% | ||||
| 7 | PCM#2 | 100% | 7 | 53.8% | −46.2% | ||||||||||||||
| 4 | PCM#3 | 100% | 4 | 80.0% | −20.0% | ||||||||||||||
| 1 | PCM#4 | 100% | 1 | 100% | |||||||||||||||
| 1 | PCM#5 | 100% | 1 | 7.7% | −92.3% | ||||||||||||||
| #2 (min filtering) | 1 | PCM#1 | 100% | 1 | 7.7% | −92.3% | |||||||||||||
| 7 | PCM#2 | 85.7% | 14.3% | 6 | 1 | 18.8% | 20.0% | −67.0% | 5.7% | ||||||||||
| 13 | PCM#3 | 69.2% | 30.8% | 9 | 4 | 28.1% | 30.8% | −41.1% | |||||||||||
| 14 | PCM#4 | 7.1% | 14.3% | 14.3% | 1 | 2 | 2 | 3.1% | 15.4% | 40.0% | −4.0% | 1.1% | 25.7% | ||||||
| 8 | PCM#5 | 50.0% | 37.5% | 12.5% | 4 | 3 | 1 | 12.5% | 23.1% | 100% | −37.5% | −14.4% | 87.5% | ||||||
| 5 | PCM#6 | 20.0% | 40.0% | 40.0% | 1 | 2 | 2 | 3.1% | 15.4% | 40.0% | −16.9% | −24.6% | |||||||
| 3 | PCM#7 | 66.7% | 33.3% | 2 | 1 | 6.3% | 7.7% | −60.4% | −25.6% | ||||||||||
| Lagend | 0% | 0–20% | 20–40% | 40–60% | 60–80% | ≥80%% | PCA < 0 | MOD > 0 | |||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsiotas, D.; Krabokoukis, T.; Polyzos, S. Detecting Tourism Typologies of Regional Destinations Based on Their Spatio-Temporal and Socioeconomic Performance: A Correlation-Based Complex Network Approach for the Case of Greece. Tour. Hosp. 2021, 2, 113-139. https://doi.org/10.3390/tourhosp2010007
Tsiotas D, Krabokoukis T, Polyzos S. Detecting Tourism Typologies of Regional Destinations Based on Their Spatio-Temporal and Socioeconomic Performance: A Correlation-Based Complex Network Approach for the Case of Greece. Tourism and Hospitality. 2021; 2(1):113-139. https://doi.org/10.3390/tourhosp2010007
Chicago/Turabian StyleTsiotas, Dimitrios, Thomas Krabokoukis, and Serafeim Polyzos. 2021. "Detecting Tourism Typologies of Regional Destinations Based on Their Spatio-Temporal and Socioeconomic Performance: A Correlation-Based Complex Network Approach for the Case of Greece" Tourism and Hospitality 2, no. 1: 113-139. https://doi.org/10.3390/tourhosp2010007
APA StyleTsiotas, D., Krabokoukis, T., & Polyzos, S. (2021). Detecting Tourism Typologies of Regional Destinations Based on Their Spatio-Temporal and Socioeconomic Performance: A Correlation-Based Complex Network Approach for the Case of Greece. Tourism and Hospitality, 2(1), 113-139. https://doi.org/10.3390/tourhosp2010007