Adaptive Computation of Multiscale Entropy and Its Application in EEG Signals for Monitoring Depth of Anesthesia During Surgery

Abstract

Entropy as an estimate of complexity of the electroencephalogram is an effective parameter for monitoring the depth of anesthesia (DOA) during surgery. Multiscale entropy (MSE) is useful to evaluate the complexity of signals over different time scales. However, the limitation of the length of processed signal is a problem due to observing the variation of sample entropy (S_E) on different scales. In this study, the adaptive resampling procedure is employed to replace the process of coarse-graining in MSE. According to the analysis of various signals and practical EEG signals, it is feasible to calculate the S_E from the adaptive resampled signals, and it has the highly similar results with the original MSE at small scales. The distribution of the MSE of EEG during the whole surgery based on adaptive resampling process is able to show the detailed variation of S_E in small scales and complexity of EEG, which could help anesthesiologists evaluate the status of patients.

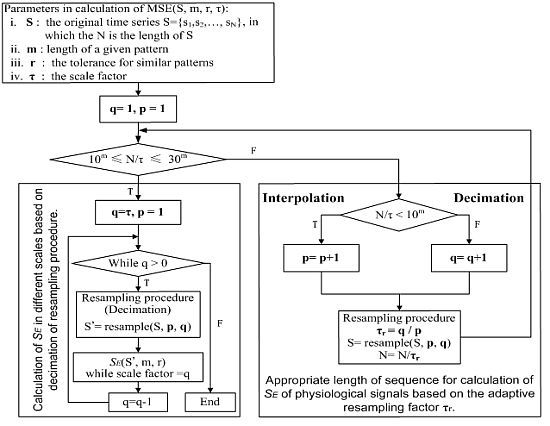
1. Introduction

Accurate measurement of the depth of anesthesia (DOA) has been a longstanding project in medical and biomedical engineering research. Nowadays, the combination of clinical observations of experienced anesthesiologists and the physiological signals detected by various monitoring devices contributes to guarantee the safety of patients and avoid mortality caused by excessive anesthetic dose and the intra-operative awareness caused by inadequate anesthesia during different kinds of surgeries. Moreover, the physiological signals of the patient can offer evidence to determine the status of the patient directly and objectively. Electroencephalography (EEG), normally measured non-invasively through scalp electrodes, reflects the spontaneous electrical activities of the human brain over a short period of time, according to the analysis of which the state of human can be determined [1,2]. However, EEG signals are difficult to detected by linear analysis techniques because of their integration of nonlinear and complex components like the rhythmic activity of brain, biological artifacts, and environmental artifacts. Therefore, with respect to the characteristics of EEG, EEG signals are analyzed through nonlinear complexity methods, which is estimated based on various algorithms of entropy theory in the time domain.

On the basis of continuous development of research on the relationship between EEG and status of the patient, the main analytic target has been to monitor DOA in studies and clinical applications, and most of current electrophysiological monitors on the market are based on the analysis of EEG, such as the Narcotrend monitor [3], the bispectral index (BIS) monitor [4], and the response entropy (RE) and state entropy (SE) in the Datex-Ohmeda S/5 entropy module [5]. However, these all monitors have some limitations. The Narcotrend unit does not adequately detect the transition between awareness and unconsciousness in surgical patients [6]. The BIS index has been recently proposed to be unresponsive to some anesthetic agents such as ketamine and nitrous oxide [7]. In addition, the BIS monitor only provides highly reliable EEG signals uncorrupted by any kind of artifacts, and the artifacts do not appear if they are not detected or excessive. Nevertheless, the RE and SE consider the different frequency ranges of the EEG signals, which is from 0.8 Hz to 47 Hz and 0.8 Hz to 32 Hz respectively. Either the relatively reliable EEG signals or the artifacts are needed to assist anesthesiologists to estimate the anesthetic state of patients under general anesthesia.

Recently, several entropy-derived parameters utilized in analyzing nonlinear EEG signals have been proposed for the assessment of depth of anesthesia. The approximate entropy (A_E) [8] of EEG signals offered a monotonic response to the induction of propofol anesthesia under certain conditions [9]. The sample entropy (S_E) [10] is an improvement of A_E with respect to computation and accuracy of signal regularity. Furthermore, the permutation entropy (P_E) is a complexity measure developed specifically for the analysis of noisy chaotic time series [11]. In recent studies, the P_E has shown promising results as an indicator of depth of anesthesia [12]. But all these parameters emphasize the fixed range of time series without the consideration of multiple time scales. The multiscale entropy (MSE) developed by Costa et al. [13,14] is used to evaluate the complexity of signals over different time scales, thus, it has been applied effectively in analysis of physiology, biology, and geosciences data. Recently, it was also used in the analysis of EEG in epileptic rats [15] and during sevoflurane anesthesia [16]. The coarse graining procedure in MSE is considered a shortcoming that decreases the entropy rate artificially [17]. In practice, it is impossible to calculate the MSE with the scale as large as possible for clinical applications. In order to adopt both long and short sequences for real clinical applications, simulation signals have been used to prove this concept. Then, practical short sequence EEG signals are applied to monitor DOA as a comparison of the adaptive resampling procedure to the original coarse-graining of the MSE.

2. Methods

2.1. Multiscale Entropy

In order to measure the complexity of a finite length time series, MSE has two steps: at first, a “coarse-graining” procedure is applied to the entire time series. For a given time series, multiple coarse-grained time series are constructed by averaging the data points within non-overlapping windows of increasing length $\tau$. Each element of the coarse-grained time series, $y_j^{\left(\tau \right)}$ is calculated according to equation (1):

$$[y_j^{\left(\tau \right)}=\frac{1}{\tau }{{\displaystyle \sum }}_{i=\left(j-1\right)\tau +1}^{j\tau }{x}_i]$$

(1)

where $\tau$ represents the scale factor and $1\le j\le N/\tau$. The length of each coarse-grained time series is$N/\tau$. For $\tau$ = 1, the coarse-grained time series is simply the original time series itself. Secondly, S_E is calculated for each coarse-grained time series. For the coarse-grained results$\left\{y_1,y_2,y_3,\dots ,y_N\right\}$, firstly two patterns of length m $X_m\left(i\right)=\left\{y_i,\dots ,y_{i+m-1}\right\}$ and $X_m\left(j\right)=\left\{y_j,\dots ,y_{j+m-1}\right\}$ are selected to compute the number of $X_m\left(j\right)$ that meets the condition:

$$d\left[X_m\left(i\right) , X_m\left(j\right)\right]\le r\left(r\ge 0\right)$$

(2)

in which $d\left[X_m\left(i\right) , X_m\left(j\right)\right]=\text{max}\left[\left|y_{i+k},y_{j+k} \right|\right]\left(k\in \left[0,m-1\right]\right)$ and $j\in \left[1,N-m\right],i\ne j$. The $B_i^m\left(r\right)$ is the result of all $X_m\left(j\right)$similar to $X_m\left(j\right)$, and the average for $i\in \left[1,N-m\right]$ is:

$${\text{B}}^{\text{m}}\left(\text{r}\right)={\left(\text{N}-\text{m}\right)}^{-1}{{\displaystyle \sum }}_{\text{i}=1}^{\text{N}-\text{m}}{\text{B}}_{\text{i}}^{\text{m}}\left(\text{r}\right)$$

(3)

when the length increases to m + 1:

$${\text{A}}^{\text{m}}\left(\text{r}\right)={\left(\text{N}-\text{m}\right)}^{-1}{{\displaystyle \sum }}_{\text{i}=1}^{\text{N}-\text{m}}{\text{A}}_{\text{i}}^{\text{m}}\left(\text{r}\right)$$

(4)

and the function of S_E is:

$${\text{S}}_{\text{E}}\left(\text{N},\text{m},\text{r}\right)=-\text{ln}\left[{\text{A}}^{\text{m}}\left(\text{r}\right)/{\text{B}}^{\text{m}}\left(\text{r}\right)\right]$$

(5)

As suggested by [1], it is preferred that $N/\tau$ be in the range of 10^m to 30^m [18] and r can be taken as 0.1~0.2SDx, where SDx is the standard deviation of the original time series. In the whole study, the MSE is calculated with m = 2 and r = 0.15 [13].

2.2. Adaptive Resampling Procedure

The process of resampling includes the interpolation in that a sequence of zero-valued samples is inserted into the input sample first, then a low-pass finite impulse response (FIR) filter is used to filter the sequence with new length, and the decimation in which a polyphase filter is applied to downsampling [19]. The sequence is interpolated by the factor p and then is decimated by the factor q, so that the resampling rate is changed into $\text{p}/\text{q}$ times the original sampling rate. ${\mathsf{\tau }}_{\text{r}}$ is referred to as a resampling factor which is equal to q divided by p. Note that p and q must be positive integers. The length of resampled sequence is the integer of the product of length of input x and $1/{\mathsf{\tau }}_{\text{r}}$. Furthermore, according to the Nyquist’s theorem, the frequency range of resampled sequence is less than or equal to $1/2{\mathsf{\tau }}_{\text{r}}$ times original sampling frequency. When p = 1 and q > 1, the resampling process is the decimation with the factor q, and the sampling rate is lower. When q > 1 and p > 1, the resampling process is the interpolation with the factor p and the sampling rate is greater. Figure 1 describes the resampling results of a simulated signal. Figure 1(a) is the original signal combining two sine waves with 30 Hz and 60 Hz, Figure 1(b) is the result of decimation of (a) with ${\mathsf{\tau }}_{\text{r}}=4$, so the resampling rate is 1/4 times original one, and Figure 1(c) result of interpolation of (a) with ${\mathsf{\tau }}_{\text{r}}=4/3$, the resampling rate is 3/4 times original one.

Figure 1. (a) The original signal combining two sine waves with 30 Hz and 60 Hz. (b) The result of decimation of (a) with ${\tau }_r=4$. (c) The result of interpolation and decimation of (a) with ${\tau }_r=4/3$.

Figure 1. (a) The original signal combining two sine waves with 30 Hz and 60 Hz. (b) The result of decimation of (a) with ${\tau }_r=4$. (c) The result of interpolation and decimation of (a) with ${\tau }_r=4/3$.

According to the function of resampling procedure, the interpolation can increase the sampling rate to provide adequate data for calculating S_E, and the decimation can obtain the original time series in different scales based on decreasing the sampling rate. Therefore, with respect to the limitation of$N/\tau$ [18], the computation of MSE of the physiological signals based on an adaptive resampling procedure is implemented as follows:

(1)

The input for MSE includes: (i) S is the original time series, and S={s₁,s₂,…, s_N}, in which N is the length of time series S; (ii) m is the length of the given pattern; (iii) r is the tolerance for the similar patterns; (iv) τ is the self-defined scale factor.

(2)

Determination of the condition of 10^m ≤ N/τ ≤ 30^m for calculating the S_E in each scale.

(3)

Calculation of S_E in the scale ranging from 1 to τ based on the resampling procedure with decimation factor q = τ and interpolation factor p = 1 if the condition in (2) is satisfied.

(4)

If the condition in (2) is not satisfied, the original time series S is resampled based on the adaptive resampling factor ${\mathsf{\tau }}_{\text{r}}$ and the resampled results has the new length of N/${\mathsf{\tau }}_{\text{r}}$. Then go back to (2).

The flowchart of the whole process is shown in Figure 2. After the appropriate length of sequence for calculation of S_E of physiological signal is obtained, the adaptive resampling factor ${\mathsf{\tau }}_{\text{r}}$ is used to change the resampling rate, the S_E in each scale is calculated according to the scale factor τ based on the decimation of resampling procedure when p = 1. If p > 1, then the S_E in each scale is computed by the resampled results based on both of the interpolation factor p and the decimation factor q. Thereby, it is possible to overcome the limitation of original MSE in analysis of physiological signals and set the relevant parameters as required.

Figure 2. The flowchart of computation of MSE based on adaptive resampling procedure.

Figure 2. The flowchart of computation of MSE based on adaptive resampling procedure.

3. Comparative Analysis of Coarse-Graining and Adaptive Resampling Procedure in MSE

In order to compare coarse-graining with the adaptive resampling procedure in MSE, the algorithm is tested on two synthetic signals of known MSE expression from a previous study [13]. The first one is a 1/f noise that is also called pink noise, its feature is that the power spectral density is inversely proportional to the frequency (long-range correlated). The second synthetic signal is a white Gaussian noise, which has normal distribution and statistically independent values at any pairs of times (random noise). A long sequence with 30,000 samples is enough to calculate MSE into a big scale. The scale factor can be up to 50 if S_E is computed in each 600 samples once. Adaptive resampled results are obtained while ${\mathsf{\tau }}_{\text{r}}=\mathsf{\tau }$, so the ${\mathsf{\tau }}_{\text{r}}$ is the decimal factor and the decimation is applied to these noises. Consequently, the coarse-grained results are compared to the adaptive resampled ones in each scale statistically. The correlation coefficients of the two noises are displayed in Figure 3(a). The red circles and blue stars are the mean of 100 subsamples of two noises obtained by the bootstrap in each scale, and bar is the standard deviation. It is obvious that the mean of correlation coefficient of 1/f noise decreases at first 10 scale factors, then keeps relatively stable above 0.9. However, the correlation coefficient of white Gaussian noise is less and less following the increasing scale factor, and the standard deviation becomes bigger gradually. For the long-range correlated noise, the two procedures have some similarity, however, for the uncorrelated noise, they are totally different. Nevertheless, Figure 3(b) shows some interesting results. The S_E calculated by resampled results (red star) is also capable of representing properties of the two known synthetic signals too, even if adaptive resampling procedure (decimation) is different with the coarse-graining procedure in analysis of the white noises.

Figure 3. (a) The correlation coefficients of white Gaussian noise and 1/f noise processed by the coarse-graining and adaptive resampling (decimation) in long sequence (30,000 samples). (b) S_E based on coarse-graining (c-g) and resampling (r-s) procedures in each scale.

Figure 3. (a) The correlation coefficients of white Gaussian noise and 1/f noise processed by the coarse-graining and adaptive resampling (decimation) in long sequence (30,000 samples). (b) S_E based on coarse-graining (c-g) and resampling (r-s) procedures in each scale.

For the sequence with long enough length, the S_E calculated from coarse-grained and adaptive resampled results give similar results. Consequently, two kinds of these noises with 3,000 samples are generated, and every 150 samples is used to calculate the S_E. The interpolation of resampling is utilized to increase the sampling rate and length of sequences. Figure 4(a) is the original MSE of two noises. Figure 4(b–d) show the S_E of adaptive resampled results in different scales while $\mathsf{\tau }={\mathsf{\tau }}_{\text{r}}$, $\mathsf{\tau }={\mathsf{\tau }}_{\text{r}}/2$, and $\mathsf{\tau }={\mathsf{\tau }}_{\text{r}}/4$ respectively, in which $\text{ τ}\in \left[1,20\right]$. First of all, the MSE of two noises acquired through two different procedures are similar with each other for the short sequence, shown in Figure 4(a,b). In Figure 4(c,d), it is evident that the scale factor $\mathsf{\tau }$ is smooth and decimate while interpolation of resampling is employed to increase the length of original short sequence. Moreover, if the analyzed signal has clear frequency range, the resampling factor ${\mathsf{\tau }}_{\text{r}}$ can tell the particular frequency range that the resampled sequence has. However, due to the elimination of fast temporal scale by coarse-graining procedure and limitation of the length of sequence for S_E, the information in these scales is missed.

Figure 4. (a) The original MSE in short sequence (3,000 samples). (b) S_E based on resampling procedures in each scale while $\tau ={\tau }_r$(decimation), (c) while $\tau ={\tau }_r/2$ (interpolation), and (d) while $\tau ={\tau }_r/4$(interpolation).

Figure 4. (a) The original MSE in short sequence (3,000 samples). (b) S_E based on resampling procedures in each scale while $\tau ={\tau }_r$(decimation), (c) while $\tau ={\tau }_r/2$ (interpolation), and (d) while $\tau ={\tau }_r/4$(interpolation).

In addition, the computation time of coarse-graining and adaptive resampling procedure is used to acquire the white Gaussian noise in the scale ranging from 1 to 20 with increasing length as displayed in Figure 5. It is explicit that less time is spent through the adaptive resampling procedure than the coarse-graining procedure while the length of samples is bigger than 2.5 × 10⁴, and the coarse-graining procedure is close to the adaptive resampling procedure in the samples that has length less than 2.5 × 10⁴. For the calculation of S_E at each scale based on the two functions in adaptive resampling procedure, there is little difference between interpolation and decimation while$\text{ τ}={\mathsf{\tau }}_{\text{r}}/2$ and $\tau ={\tau }_r/4$before 9 × 10⁴. Nevertheless, when N is bigger than 9 × 10⁴, the computation time of both coarse-graining and adaptive resampling procedure while $\mathsf{\tau }={\mathsf{\tau }}_{\text{r}}/2,\tau ={\tau }_r/4$ increases suddenly. However, the latter is still less than that of the coarse-graining procedure. The experiment results are calculated by an ordinary computer (Inter® Core^TM2 Duo CPU T6400 2.00 GHz and RAM 1.20 GHz 3GB). Thus the adaptive resampling procedure has the advantage in computing speed of the sequence in different scales for long sequences.

Figure 5. The time of calculating the white Gaussian noise with an increasing length in scale range from 1 to 20 through the coarse-graining and adaptive resampling procedure respectively.

Figure 5. The time of calculating the white Gaussian noise with an increasing length in scale range from 1 to 20 through the coarse-graining and adaptive resampling procedure respectively.

In order to compare the coarse-graining and adaptive resampling (decimation) process in analysis of the frequency of complex signals by combining the 1/f noise with a sine wave with a fixed frequency. The frequency range of sine waves is from 1 Hz to 30 Hz, and the sampling rate is 100 Hz. The length of data is 30,000. The adaptive resampled results are obtained while ${\mathsf{\tau }}_{\text{r}}=\mathsf{\tau }$. Figure 6 shows the results of the original MSE and the MSE with adaptive resampling procedure. The horizontal axis is the scale factor and the vertical axis is the frequency of each sine wave added into the 1/f noise. The color represents the value of S_E, the color bar shows the value range. In Figure 6(a,b), the maximum of S_E locates at increasing scale following by the decreasing frequency of sine wave, which means the frequency range of signals analyzed by MSE is reduced by the scale factor. In Figure 6(a), the boundary among each scale is too vague to distinguish, and the distribution of frequency of the combined signal is also not obvious. But in Figure 6(b), the boundary is clear ant the main distribution of each sine wave has located in each scale evidently (see the deep red color, the entropy value of which is up to 2.3). For example, when ${\mathsf{\tau }}_{\text{r}}=\mathsf{\tau }=2$, the resampling frequency is one quarter of 100. The entropy value that is greater than 1.9 covers from 2 Hz to 24 Hz approximately.

Thereby, the adaptive resampling (decimation) procedure as an alternative to the coarse-graining procedure in MSE is proved to be feasible. The decimation of adaptive resampling produces similar results as coarse-graining in computing S_E, and the interpolation of adaptive resampling is able to improve the analysis of more scales in short sequences. Furthermore, the frequency range of resampled sequences can be figured out by the resampling frequency, so that it establishes a relationship between the complexity and the frequency range of signals.

Figure 6. (a) The distribution of original MSE of the combined signals (30,000 samples). (b) The MSE distribution of based on resampled results while $\tau ={\tau }_r$(decimation). [The combined signal is composed by a 1/f noise and a sine wave with a fixed frequency (1~30 Hz)].

Figure 6. (a) The distribution of original MSE of the combined signals (30,000 samples). (b) The MSE distribution of based on resampled results while $\tau ={\tau }_r$(decimation). [The combined signal is composed by a 1/f noise and a sine wave with a fixed frequency (1~30 Hz)].

4. Application of MSE to analysis of EEG for Monitoring DOA

In analysis of EEG signals through the MSE with the coarse-graining procedure and adaptive resampling (decimation) procedure, four kinds of EEG signals are selected, shown in Figure 7(a–d). They were recorded in: (a) eye opened with consciousness, (b) eye closed and rolling with consciousness, (c) filtered result of (b) through the method of noise-assisted multivariate empirical mode decomposition (N-A MEMD) [20], (d) anesthetic state during the surgery. The S_E of the two procedures in each scale are shown in Figure 7(e–h), coarse-grained results are blue dots, and the adaptive resampled results are red stars. It is significant that the electrooculography (EOG) should be eliminated because of its serious disturbances on the results of both. Figure 7(e,f) display the high complexity on only low frequency and big scale, the high frequency of consciousness can be reconstructed by IMF1~3 of N-A MEMD, shown in Figure 7(c) and thus it has the high complexity at small scale, shown in Figure 7(g). In anesthetic state, the complexity focus on the low frequency and big scale, and the entropy value is up to 2 while the scale is greater than 10, shown in Figure 7(h).

Figure 7. (a) EEG of eye opened with consciousness. (b) EEG of eye closed and rolling with consciousness. (c) filtered EEG of (b) through the method of N-A MEMD. (d) EEG of anesthetic state during the surgery; (e), (f) ,(g) and (h) are the MSE of (a), (b), (c) and (d) based on coarse-graining (blue dots) and resampled(decimation) (red stars) process respectively.

Figure 7. (a) EEG of eye opened with consciousness. (b) EEG of eye closed and rolling with consciousness. (c) filtered EEG of (b) through the method of N-A MEMD. (d) EEG of anesthetic state during the surgery; (e), (f) ,(g) and (h) are the MSE of (a), (b), (c) and (d) based on coarse-graining (blue dots) and resampled(decimation) (red stars) process respectively.

In this study, the EEG signals are collected from twenty patients, whose ages ranged from 15 to 60, undergoing urological surgery with general anesthesia at the Far Eastern Memorial Hospital of Taiwan after obtaining the permission of the patients and the hospital. The monitoring EEG device is a Datex-Ohmeda S/5^TM Compact Anesthesia Monitor within which the sampling rate of EEG signals is 100 Hz. The anesthetic in the operations is propofol. According to the operation standard procedure, the operation time has been divided into four procedures: the pre-operation, induction, maintenance and recovery. One set of EEG recordings of a male patient, age 15, who underwent urological surgery and experimental results are given and shown in the Figure 8. Figure 8(a) is the original EEG recording, and after the EOG in pre-operation is filtered by N-A-MEMD, as shown in Figure 8(b). The real time RE and SE recordings during the surgery are the black dashed line and red solid line respectively in Figure 8(c), Figure 8(d) shows the S_E of Figure 8(b) while ${\tau }_r=\tau =1$, which is calculated from EEG recordings in a time window of 30 seconds including 3,000 points of EEG signals. In order to be consistent with the RE and SE recordings, the sliding window moves every five seconds once for real time analysis. The S_E of EEG without the EOG is similar with the RE and SE.

Under these conditions, the correlation is calculated for the distribution of S_E in each scale during the entire operation based on coarse-graining and adaptive resampling procedure respectively. In Figure 9, the colored bar represents the variation of S_E and complexity intensity through different colors. The deep red color represents the EEG with high complexity and the blue color illustrates the EEG with low complexity, so the red color exists in the pre-operation and recovery and blue color exists in the maintenance at small scales. Figure 9(a) shows the original MSE during the whole surgery based coarse-graining procedure in scale 1 to 10. Figure 9(b–d) are the distribution of S_E in scale 1 to 10 during the entire operation by adaptive resampling procedure with $\tau ={\tau }_r$,$\tau ={\tau }_r/2$,$\tau ={\tau }_r/4$. Figure 9 (e–h) are the vertical views of (a–d), and Figure 9(i–l) are the side views of (a–d) from time axis.

Figure 8. (a) The original EEG recording during the urological surgery of a male patient, age 15. (b) The EEG recording without disturbance of EOG through N-A MEMD. (c) The entropy index of RE and SE collected by Datex-Ohmeda S/5^TM Compact Anesthesia Monitor during the whole surgery. (d) S_E of (b).

Figure 8. (a) The original EEG recording during the urological surgery of a male patient, age 15. (b) The EEG recording without disturbance of EOG through N-A MEMD. (c) The entropy index of RE and SE collected by Datex-Ohmeda S/5^TM Compact Anesthesia Monitor during the whole surgery. (d) S_E of (b).

Figure 9. The S_E calculated during the whole surgery by coarse-graining procedure and adaptive resampling procedure with three conditions$\tau ={\tau }_r$,$\tau ={\tau }_r/2$,$\tau ={\tau }_r/4$ in scale 1~10. (a) The original MSE. (b) The MSE based on adaptive resampled results while $\tau ={\tau }_r$. (c) The MSE based on adaptive resampled results while$\tau ={\tau }_r/2$. (d) The MSE based on adaptive resampled results while$\tau ={\tau }_r/4$. (e–h) The vertical views of (a–d). (i–l) The side views of (a–d) from time axis.

Figure 9. The S_E calculated during the whole surgery by coarse-graining procedure and adaptive resampling procedure with three conditions$\tau ={\tau }_r$,$\tau ={\tau }_r/2$,$\tau ={\tau }_r/4$ in scale 1~10. (a) The original MSE. (b) The MSE based on adaptive resampled results while $\tau ={\tau }_r$. (c) The MSE based on adaptive resampled results while$\tau ={\tau }_r/2$. (d) The MSE based on adaptive resampled results while$\tau ={\tau }_r/4$. (e–h) The vertical views of (a–d). (i–l) The side views of (a–d) from time axis.

The similarity is shown to be above 90 percent of S_E between coarse-graining and adaptive resampling process at small scales of EEG from 1 to 6 while $\tau ={\tau }_r$ for decimation, as shown in Table 1. While the interpolation is applied with $\tau ={\tau }_r/2$,$\tau ={\tau }_r/4$, the distribution of S_E within scale 1 to 5 in Figure 9(b) is amplified into 2 and 4 times in Figure 9(c,d), which is able to supply more information about the variation of complexity of EEG on the original small scales. Thus, the interpolation is a necessity in adaptive resampling procedure on the basis of its detailed function. Further statistical correlation coefficients between S_E and RE/SE in twenty urological surgeries are shown in Table 2. The S_E is calculated on a scale of 1 to 6 by the coarse-graining process and adaptive resampling process for three cases $\tau ={\tau }_r$,$\tau ={\tau }_r/2$,$\tau ={\tau }_r/4$, because the high correlation coefficients in Table 1 concentrate on the scales from 1 to 6 and the coefficients are expressed as mean ± S.D. When $\tau ={\tau }_r$=1, scale = 1 without interpolation, the S_E is highly relevant to the RE and SE, and both correlation coefficients are above 0.9. Thereby, the S_E of EEG at scale 1 is able to monitor the DOA during the whole operation. However, decreasing correlation coefficients follow the increasing scale factor in coarse-graining and adaptive resampling procedures, which means S_E at large scales of EEG only describes the complexity of EEG at lower frequency range and is inappropriate to express the status of patients undergoing operations. In this situation, interpolation factor of adaptive resampling process is helpful to get more details at the small scales. It is obvious to find high correlation coefficients between S_E and RE/SE among a scale of 1 to 6 when interpolation is used, as shown in Table 2. When $\tau ={\tau }_r/2$, there are scale 1 and 2 at which the S_E based on adaptive resampling procedure has at least 90 percent similarity with RE/SE, and it is the same in the almost 5 scales ranging from 1 to 5 when $\tau ={\tau }_r/4$. Therefore, the MSE is a useful tool for observing the distribution of the complexity of EEG in different scales, and the adaptive resampling procedure can give more detailed results than the coarse-graining procedure at small scales.

Table 1. Correlation coefficients of the S_E in scale 1 to 10 between coarse-graining and adaptive resampling processes while $\tau ={\tau }_r$(decimation) during the whole urological surgery.

Scale factor (τ = τr)	1	2	3	4	5	6	7	8	9	10
coarse-graining vs. adaptive resampling	1	0.9855	0.9233	0.9152	0.9142	0.9045	0.897	0.8847	0.8796	0.8672

Table 1. Correlation coefficients of the S_E in scale 1 to 10 between coarse-graining and adaptive resampling processes while $\tau ={\tau }_r$(decimation) during the whole urological surgery.

Scale factor (τ = τr)	1	2	3	4	5	6	7	8	9	10
coarse-graining vs. adaptive resampling	1	0.9855	0.9233	0.9152	0.9142	0.9045	0.897	0.8847	0.8796	0.8672

Table 2. Correlation coefficients between RE/SE and the S_E in scale 1 to 6 computed by coarse-graining and adaptive resampling processes in the twenty urological surgeries.

Scale factor	SE (τ, coarse-graining)		SE $\mathbf{(}\mathit{\tau }\mathbf{=}{\mathit{\tau }}_{\mathit{r}}$, decimation)		SE $\mathbf{(}\mathit{\tau }\mathbf{=}{\mathit{\tau }}_{\mathit{r}}\mathbf{/}\mathbf{2}$, interploation)		SE ($\mathit{\tau }\mathbf{=}{\mathsf{\tau }}_{\mathbf{r} }\mathbf{/}\mathbf{4}$, interpolation)
	RE	SE	RE	SE	RE	SE	RE	SE
1	0.917 ± 0.01	0.940 ± 0.01	0.917 ± 0.01	0.940 ± 0.01	0.917 ± 0.01	0.917 ± 0.01	0.899 ± 0.01	0.928 ± 0.01
2	0.678 ± 0.03	0.714 ± 0.03	0.655 ± 0.04	0.686 ± 0.03	0.919 ± 0.01	0.942 ± 0.005	0.907 ± 0.01	0.916 ± 0.01
3	−0.262 ± 0.03	−0.234 ± 0.02	−0.358 ± 0.02	−0.347 ± 0.03	0.86 ± 0.01	0.89 ± 0.01	0.920 ± 0.01	0.938 ± 0.01
4	−0.633 ± 0.02	−0.624 ± 0.02	−0.711 ± 0.02	−0.721 ± 0.01	0.655 ± 0.02	0.682 ± 0.03	0.918 ± 0.01	0.938 ± 0.01
5	−0.698 ± 0.01	−0.711 ± 0.01	−0.744 ± 0.01	−0.754 ± 0.01	0.278 ± 0.04	0.293 ± 0.04	0.902 ± 0.01	0.926 ± 0.00
6	−0.714 ± 0.02	−0.730 ± 0.01	−0.69 ± 0.02	−0.702 ± 0.01	−0.355 ± 0.01	−0.348 ± 0.01	0.862 ± 0.01	0.886 ± 0.01

Table 2. Correlation coefficients between RE/SE and the S_E in scale 1 to 6 computed by coarse-graining and adaptive resampling processes in the twenty urological surgeries.

Scale factor	SE (τ, coarse-graining)		SE $\mathbf{(}\mathit{\tau }\mathbf{=}{\mathit{\tau }}_{\mathit{r}}$, decimation)		SE $\mathbf{(}\mathit{\tau }\mathbf{=}{\mathit{\tau }}_{\mathit{r}}\mathbf{/}\mathbf{2}$, interploation)		SE ($\mathit{\tau }\mathbf{=}{\mathsf{\tau }}_{\mathbf{r} }\mathbf{/}\mathbf{4}$, interpolation)
	RE	SE	RE	SE	RE	SE	RE	SE
1	0.917 ± 0.01	0.940 ± 0.01	0.917 ± 0.01	0.940 ± 0.01	0.917 ± 0.01	0.917 ± 0.01	0.899 ± 0.01	0.928 ± 0.01
2	0.678 ± 0.03	0.714 ± 0.03	0.655 ± 0.04	0.686 ± 0.03	0.919 ± 0.01	0.942 ± 0.005	0.907 ± 0.01	0.916 ± 0.01
3	−0.262 ± 0.03	−0.234 ± 0.02	−0.358 ± 0.02	−0.347 ± 0.03	0.86 ± 0.01	0.89 ± 0.01	0.920 ± 0.01	0.938 ± 0.01
4	−0.633 ± 0.02	−0.624 ± 0.02	−0.711 ± 0.02	−0.721 ± 0.01	0.655 ± 0.02	0.682 ± 0.03	0.918 ± 0.01	0.938 ± 0.01
5	−0.698 ± 0.01	−0.711 ± 0.01	−0.744 ± 0.01	−0.754 ± 0.01	0.278 ± 0.04	0.293 ± 0.04	0.902 ± 0.01	0.926 ± 0.00
6	−0.714 ± 0.02	−0.730 ± 0.01	−0.69 ± 0.02	−0.702 ± 0.01	−0.355 ± 0.01	−0.348 ± 0.01	0.862 ± 0.01	0.886 ± 0.01

In our previous study [21], the sum of S_E in each scale at every second was thought to be a complexity index for monitoring DOA, like in analysis of heart rate [13,14]. Nevertheless, this complexity index seems not be adaptive to the analysis of EEG. The problems that have been met are: (1) the limitation of data length in real time analysis due to the low sampling rate of EEG signals; (2) only one line to describe the MSE in every second is insufficient to establish the relationship between MSE and the variation of patients’ status. After introduce of the adaptive resampling procedure in computing MSE of EEG in different scales, those problems are resolved. Because the MSE based on adaptive resampling process not only can provide the similar results of complexity of EEG with the original MSE at small scales, it also is able to give more information for observing the distribution of S_E at small scales during the whole time while $\mathsf{\tau }={\mathsf{\tau }}_{\text{r}}/\text{p}$, p is the factor for interpolation.

5. Discussion and Conclusions

According to the analysis of the coarse-graining and the adaptive resampling procedure in computing MSE, the adaptive resampling process can be an alternative to the coarse-graining procedure for computing the S_E in the two synthetic signals, which are the white Gaussian noise and 1/f noise. Moreover, so does in the analysis of various EEG signal recorded in different states of subjects. In addition, the interpolation as one aspect in adaptive resampling procedure can smooth the original MSE at small scales when the sampling rate of signal is small and there are not enough samples for computing S_E in more scales.

In monitoring the DOA during the whole surgeries, the MSE in every second has no direct index to evaluate the state of patients. However, the MSE with enough scales based on the adaptive resampling procedure can provide the variation of the in S_E at real time because it needs less computation time than the coarse-graining process. Additionally, it is important that the EOG should be filtered at first, thus, the algorithm and method for getting the pure EEG signals are important for our works at the same time. So far, the empirical mode decomposition (EMD) [22] and some extensive methods [23,24] should be used in our study in the near future.

In conclusion, the process of coarse-graining in MSE can be replaced with the adaptive resampling procedure for both long and short sequences because of the high speed of computation and more useful details at small scales. Furthermore, the distribution of MSE of EEG during the whole surgery based on adaptive resampling process is able to show the detailed variation of S_E in small scales and complexity of the patient’s EEG recordings, which could help anesthesiologists to evaluate the status of patients.