1. Introduction
The dynamics of the uppermost part of the atmosphere of the Sun, known as the solar corona, is one of the key elements of the magnetohydrodynamic (MHD) interaction of the Sun with the Earth and other planets and is important for basic plasma physics. Understanding how the solar corona is structured in three dimensional (3D) space is a challenging and not a trivial task. Excluding solar eclipses, which allow us to see the corona in visible light for only a few minutes, routine observations from telescopes or coronagraphs aboard spacecraft (such as the Solar and Heliospheric Observatory (SoHO), the Transition Region And Coronal Explorer (TRACE), the Solar TErrestrial RElations Observatory (STEREO), Hinode and, more recently, the Solar Dynamics Observatory (SDO) at extreme ultra-violet (EUV) and X-ray bandpasses are the main source of information about the complex dynamics of the corona. In these bands, the corona is usually an
optically thin medium: an emitted photon can go through it without experiencing any noticeable absorption or scattering. This seriously affects the identification or tracking of important features (e.g., coronal loops and plumes) in imaging data obtained from a single point of observation. A crucial parameter in this sense is the column depth [
1,
2], which gives a measure of how much the intensity of a given structure is integrated along the line-of-sight (LOS).
The launch of STEREO in 2006 has opened the possibility to make stereoscopy, thanks to the twin spacecraft observing the Sun at about 1 AU, but with two different LOS [
3]. The STEREO mission’s aim is to understand the 3D structure of coronal mass ejections (CMEs) and their impact on the solar system and Earth environment (see [
4]), but it is suitable also for 3D reconstruction of the geometry of loops in coronal active regions (ARs) (for a review of the topic, see [
5]). In particular, observations show that coronal loops are subject to transverse (kink) oscillations (e.g., [
6,
7,
8,
9,
10,
11]). These oscillations are a good tool for the diagnostics of the magnetic field inside the loop, which depends on the period of the kink oscillations, its length, the plasma density [
12] and the loop’s sub-resolution structuring [
13]. Therefore, a better estimate of the loop length could easily improve the inference of the field. The value of the field is one of the decisive parameters of AR for answering the enigmatic questions of solar and stellar physics, such as the mechanisms for coronal heating and flaring energy releases, coronal mass ejections and the solar and stellar wind acceleration.
A forward-modelling 3D loop reconstruction method has been developed by Verwichte [
14,
15] in the context of studying kink oscillations of coronal loops and reducing the error in measuring loop lengths. The method works as follows. In one view, the plane-of-sky loop coordinates are traced. A third coordinate that denotes the loop observed depth is added by assuming that the loop is planar (or non-planar, following a simple geometrical model). The problem is thus reduced to finding the value of one (or a few) parameters, such as the inclination angle of the loop plane with respect to the normal to the solar surface. For a range of inclination angles, the loop is forward-modelled to a new view, and the angle with the best fit is determined visually. In [
14,
15], a second viewpoint was absent. In the first study, a second viewpoint was created from the data from several days later, using the change of the LOS by the solar rotation. In many respects, this method is then akin to the dynamic stereoscopy method by Aschwanden [
16]. In the second study, the inclination angle is found by minimising the variation in curvature. Later, this method had been applied to loops seen simultaneously with SDO and STEREO [
10,
17,
18,
19]. This method has the advantage of not requiring accurate tracing of the loop from both views and does not impose a specific shape of the loop (e.g., semi-circular), except for planarity. Because of the difference in the spatial resolution between the Atmospheric Imaging Assembly (AIA) in SDO and the Extreme Ultra Violet Imager (EUVI) in STEREO, tracing a loop in the AIA view and forward-modelling to the EUVI view gives the best results.
In a strict sense, 3D reconstruction is performed by observations of a solar feature from at least two observers placed at different positions—a technique that is called “stereoscopy”—and allows for the determination of the 3D coordinates in the space of an observed point (for an explanation of the principles of stereoscopy, see [
5,
20,
21]; a description is given at [
22], The SolarSoftWare (SSW) package [
23] provides useful tools for making 3D reconstruction, e.g., the procedures
scc_measure.pro [
24] or
sunloop.pro [
25]. The former includes a widget application (see
Figure 1 for a typical graphical output) that enables the user to select with the cursor a solar feature of interest appearing in both perspectives from one of the STEREO spacecraft (but it is also possible to combine SDO and the one of STEREO spacecraft). By selecting a point in one image, the program displays a line in the other image representing the LOS from the first image (or the epipolar line). The user then selects the point along this line with the same feature. The 3D coordinates are then calculated as (Earth-based) Stonyhurst heliographic longitude and latitude, along with the radial distance in solar radii. The coordinates can be easily converted into the Heliocentric Earth Equatorial (HEEQ) coordinates for a Cartesian representation of the data (for a complete review of the coordinate systems, please refer to [
26]).
Figure 1.
Graphical output of the procedure
scc_measure: the windows give the field of view (FOV) from STEREO-A ( right) and STEREO-B ( left) spacecraft for a coronal loop on 27 June 2007, studied by Aschwanden [
5], Verwichte
et al. [
14].
Figure 1.
Graphical output of the procedure
scc_measure: the windows give the field of view (FOV) from STEREO-A ( right) and STEREO-B ( left) spacecraft for a coronal loop on 27 June 2007, studied by Aschwanden [
5], Verwichte
et al. [
14].
As we have seen, fitting a loop with a 1D curvilinear feature (circular or elliptical) depends on six parameters, namely: the heliographic longitude and latitude of the midpoint of the loop baseline on the solar surface, the baseline length between the two footpoints, the height of the loop, the inclination and the azimuth angle (see Section 3.4.4 of [
27]).
A representation of the loop and its main parameters are shown in
Figure 2. Recently, Gary
et al. [
28] proposed a fitting approach of loops by cubic Bézier curves, in order to distinguish between competing models for the magnetic field topology.
Figure 2.
Schematic representation of a coronal loop relative to the solar surface, with the baseline connecting the footpoints, the inclination angle relative to the normal surface and the azimuth angle relative to the east-west direction. Courtesy of Markus Aschwanden.
Figure 2.
Schematic representation of a coronal loop relative to the solar surface, with the baseline connecting the footpoints, the inclination angle relative to the normal surface and the azimuth angle relative to the east-west direction. Courtesy of Markus Aschwanden.
In this paper, we propose a new method allowing us to get the 3D shape of a loop by stereoscopic measurements, using principal component (PC) analysis. It reduces the number of parameters, dependencies and correlations between variables, by calculating a new basis of vectors, which defines the reference system relative to the loop. In the next section, we give an overview of PC analysis in the frame of 3D loop reconstruction. In
Section 4, we present some examples, discussing analysis and comparing results with previous methods, and conclusions are given in the last section.
2. Three-Dimensional Reconstruction by Principal Component Analysis
Given a set of variables, which can be interrelated, PC analysis allows us to transform this set into a new one of “uncorrelated” or independent variables, known as
principal components, but preserving the variation of the data distribution. Principal component analysis, also know as minimum variance analysis, has been applied in several research fields, e.g., in the determination of magnetic field geometry by
in situ multi-spacecraft measurements [
29]. Algebraically, PCs are particular linear combinations of the set of original variables, and geometrically, this is equivalent to the rotation of the original coordinate system into a new one, where the new axes represent the maximum variability of the dataset. Avoiding a rigorous mathematical treatment, which can be found in textbooks, such as Jolliffe [
30], Johnson and Wichern [
31], we give here a specific step-by-step description of how to fit coronal loops by PC analysis.
Given a set of
N 3D data points
(we use, for simplicity, the HEEQ system) that sample the loop shape and is represented by an
matrix
X, we can build the sample covariance matrix,
, defined as:
where
), with
and
the mean, identified as the centre
of the loop. Now, we would like to put this in a new reference frame, whose axes maximise the variances, minimise the covariances of the points and have means equal to zero. This is equivalent to finding the eigenvalues and eigenvectors that diagonalise the matrix,
S, in a matrix,
Λ. Let us obtain the eigenvalues and sort them in the ascending order, as:
The corresponding eigenvectors will be
, whose components are relative to the original frame. Thus, the matrix:
defines the basis change
, and diagonalises
S as
(since
E is the basis change matrix,
);
with
, are the coordinates of the data points in the new reference frame (they are also called “
scores” in PC analysis); the eigenvector,
, locates the normal to the loop plane,
is directed like the minor axis of the ellipse and
, like the major one. The axes values are related to the variance as (for statistical reasons, when
N is small, it can be replaced by
):
Indeed, since we have defined the covariance matrix,
, without dividing its elements by
N, this should be done for the eigenvalues (the eigenvectors remain the same despite the normalisation of
). A further justification for the presence of the factor,
, is given in
Appendix A.1. The “fitted” loop can be traced starting from the parametric equations of an ellipse:
with
, then, transformed in HEEQ coordinates,
, by the basis change with the matrix
. Those points, whose squared distance satisfies the condition
, defines the loop curve.
We can look at how much of the total variance of the data points is counted by each single eigenvalue. Let
Λ be the total variance defined as
. Then, the ratio
(with
) gives an indication of how much of the “energy” is carried out by
. According to
Table 1, most of the variance is stored in along the
directions, suggesting that the points are mostly distributed in a 2D plane. This is equivalent to saying that we have reduced the dimensionality of the dataset, by projecting it into a subspace, that is the 2D plane of the loop.
Table 1.
The table shows the main quantities used and inferred from principal component (PC) analysis: the first rows are related to the inputs and show the number of 3D points, N, and the heliographic coordinates of the supposed loop centre; then, we tabulated the total variance, Λ, and the percentage relative to each eigenvalue, λ. The last rows show the estimates of each analysed loop: the minor (a) and major radii (b) with their corresponding standard deviations, the standard deviation, , of the points from the loop plane, the inclination and azimuth angles, the eccentricity and, finally, the loop length.
Table 1.
The table shows the main quantities used and inferred from principal component (PC) analysis: the first rows are related to the inputs and show the number of 3D points, N, and the heliographic coordinates of the supposed loop centre; then, we tabulated the total variance, Λ, and the percentage relative to each eigenvalue, λ. The last rows show the estimates of each analysed loop: the minor (a) and major radii (b) with their corresponding standard deviations, the standard deviation, , of the points from the loop plane, the inclination and azimuth angles, the eccentricity and, finally, the loop length.
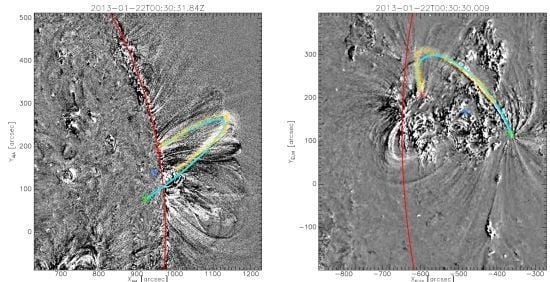
| Event | 2007-06-27 | 2013-01-21 | 2013-01-22 | 2013-01-22 | 2013-01-22 | 2013-01-22 |
|---|
| (Figure) | (3) | (4) | (5) | (6) | (7) | (8) |
|---|
| N | 15 | 15 | 30 | 22 | 14 | 19 |
| [deg] | −87.76 | 69.23 | 100.35 | 100.67 | 100.85 | 94.11 |
| [deg] | −11.41 | 25.88 | 9.25 | 9.43 | 8.84 | 6.74 |
| Λ | 0.32 | 0.21 | 1.17 | 0.91 | 0.60 | 0.17 |
| [%] | 0.24 | 0.80 | 0.04 | 0.05 | 0.09 | 0.50 |
| [%] | 11.17 | 38.04 | 26.03 | 20.86 | 19.29 | 9.51 |
| [%] | 88.59 | 61.16 | 73.93 | 79.09 | 80.61 | 89.99 |
| a [R] | 0.072 | 0.107 | 0.145 | 0.134 | 0.133 | 0.042 |
| [R] | ±0.004 | ±0.008 | ±0.006 | ±0.006 | ±0.010 | ±0.003 |
| b [R] | 0.202 | 0.136 | 0.244 | 0.262 | 0.272 | 0.130 |
| [R] | ±0.014 | ±0.004 | ±0.011 | ±0.010 | ±0.019 | ±0.007 |
| [R] | ±0.008 | ±0.011 | ±0.004 | ±0.004 | ±0.006 | ±0.007 |
| θ [deg] | 2.85 | 0.02 | 25.06 | 20.66 | 16.71 | −41.49 |
| α [deg] | 37.21 | −72.62 | −17.34 | −17.17 | −19.63 | −15.20 |
| eccentricity | 0.93 | 0.61 | 0.80 | 0.86 | 0.87 | 0.95 |
| L [Mm] | 325.22 | 276.62 | 448.30 | 457.96 | 468.77 | 203.64 |
We can obtain the inclination and azimuth angles from the orientation of the loop plane in space. The inclination angle is defined as the angle between the normal to the solar surface and the loop plane. By considering the vector,
, normal to the loop plane, we can find the inclination angle as:
where
is the normal, directed in the radial directions. The azimuthal angle is defined as the angle formed by the intersection of the loop baseline with the east-west solar direction, represented by the longitudinal vector,
. Therefore, the azimuthal angle can be found as:
The errors of the fitting can be estimated from the “scores” and their distance,
d, from the fitted curve; it is possible to give an estimate of the standard deviation of the
a and
b direction from the sum of the squared distance (see
A.2, for more details). Another possible way is to perform PC analysis for
M samples of the 3D points, or to construct synthetic samples by randomly varying the 3D original measurements within their errors (private communication: Antonio Vecchio): the best values of the radii, inclinations and azimuth angles, as well as their standard deviations, will be inferred from their distributions.
4. Conclusions
In this paper, we propose a new method for the determination of the 3D shape of coronal loops from stereoscopic measurements. The necessity to understand the loop shape is important in order to better estimate, for example, the loop length, which is a crucial parameter in inferring the magnetic field by coronal seismology (or, generally, to compare the geometry of loops, which are assumed to trace magnetic field lines in the low-
β coronal plasma, with potential field models of the coronal magnetic field [
28]). Furthermore, the loop shape determines the variation of the column depth along the loop in different phases of kink oscillations and, hence, the distribution and dynamics of the LOS-integrated intensity of the loop. The previous approach to 3D reconstruction is based on fitting stereoscopic 3D tie-points, taken along the loops. A good fitting requires a large number of points, but taking them could be a laborious task, because of high observational and instrumental noise and the effect of the LOS integration. Usually, by procedures, e.g.,
scc_measure, the number of tie-points selected is about 10–20. The method used in Aschwanden
et al. [
21] and his subsequent papers is to interpolate the 3D points with a spline, in order to retrieve the loop shape. On the other hand, this operation could add further degrees of freedom (e.g., non-planarity), and the corresponding reconstructed loop could deviate from a regular shape, like a circle or ellipse (e.g., see Figure 9 of Aschwanden
et al. [
21], and Figure 7 of Aschwanden [
5]), also because of the natural spread of the measurements around the true value. Moreover, fitting the 3D points with a 1D curvilinear feature requires the determination of the six free parameters: the inclination and azimuth angles, the length of the baseline, the loop centre position and the loop height. Conversely, all this information is implicitly stored in the distribution of a sample of 3D measurements, and it can be retrieved easily by the technique of principal components analysis. Determination of these parameters can be made by a simple step-by-step process. The technique we developed can be summarised in the followings steps:
measurement of a sample of 3D tie-points that outline the loop shape from two different LOSs;
calculation of the sample covariance matrix, , of the 3D points;
determination of the three pairs of eigenvalue/eigenvectors, , which identify the new reference frame relative to the loop, sorted in ascending order;
the smallest eigenvalues and the corresponding eigenvector is associated with the normal to the loop plane;
the largest eigenvalue/eigenvector locates the major axis and the remaining, the minor axis, according to Equation (
4);
determination of the inclination and azimuth angles according to Equations (
6) and (
7);
loop tracing with the parametric Equation (
5) and transformation in the original coordinates system, HEEQ.
The determination of the set of three vectors,
, which constitutes the new basis for the reference frame relative to the loop, depends uniquely on the choice of the loop centre (or, also, called the midpoint), which plays the role of the decisive parameter of the problem. Moreover, according to the example of the loop on 27 June 2007 (
Figure 3), we have shown that the information about the midpoint can be deduced or guessed directly from the 3D measurements, overcoming the issue of the lack of information about the loop baseline, when it is too close to the solar limb. The advantage of this method is that it works for a reasonably small number of data points (10–20), without requiring any intermediate step, like interpolation. The only assumption made in our analysis is the planarity of the loop, but possible speculations on it can be made by studying the distribution of the data points around the loop plane and searching for some possible patterns, like arcs or s-shapes, which could outline, respectively, the fundamental and second harmonic in kink oscillations. On the other hand, the relative deviation of the measurements from the best-fitted loop plane is less the 1%, probably too small in order to appreciate any non-planarity. Moreover, a further step forward for reasonable modelling of the magnetic field would be to fit the loop shape by a dipole or stretched dipole line, as suggested in Hu
et al. [
33]. These issues, as well as refinements of the technique by PC analysis could be the object of future work.