Generation and Nonlinear Dynamical Analyses of Fractional-Order Memristor-Based Lorenz Systems

Abstract

In this paper, four fractional-order memristor-based Lorenz systems with the flux-controlled memristor characterized by a monotone-increasing piecewise linear function, a quadratic nonlinearity, a smooth continuous cubic nonlinearity and a quartic nonlinearity are presented, respectively. The nonlinear dynamics are analyzed by using numerical simulation methods, including phase portraits, bifurcation diagrams, the largest Lyapunov exponent and power spectrum diagrams. Some interesting phenomena, such as inverse period-doubling bifurcation and intermittent chaos, are found to exist in the proposed systems.

1. Introduction

The memristor, a nonlinear resistor with a memory effect, was originally postulated by Chua in 1971 [1]. Because there were no such devices found in reality, research on the memristor and its application did not attract attention in the science and engineering field. Its prototype was successfully realized by researchers at Hewlett-Packard in 2008 [2]. Nowadays, the memristor has a wide range of applications in storage [3–5], neural networks [6–8], chaotic systems [9,10], and so on. It is observed that the memristor-based systems have properties that the common systems do not possess.

Recently, the memristor-based chaotic systems were becoming a research hotspot at home and abroad. In [10–13], Chua’s diodes were replaced with memristors characterized by a piecewise linear function. Bao et al. proposed an active two-terminal flux-controlled memristor characterized by a quadratic nonlinearity in [14]. In [15–18], flux-controlled memristors characterized by a smooth continuous cubic nonlinearity are presented. Furthermore, research has been done on the charge-controlled memristor characterized by a fourth degree polynomial function [19]. Compared to classical integer-order models, the fractional derivative provides a wonderful implement for describing the memory and hereditary properties of all kinds of materials and processes. Therefore, research on fractional-order systems has a more universal meaning. Recently, Ivo Petráš first studied the fractional-order memristor-based Chua’s circuit [20]. In [21], the simplest fractional-order memristor-based chaotic system is introduced. In [19], a fourth degree polynomial memristance function is used in the fractional-order memristor-based simplest chaotic circuit. The above-mentioned research results focus on the fractional-order memristor-based Chua or the simplest circuit. However, there are few results about the fractional-order memristor-based Lorenz system. In [22], an integer-order memristor-based Lorenz circuit with a piecewise linear memristance function is presented. Usually the equations of fractional-order systems are derived from the corresponding integer-order counterpart. Inspired by this, the idea of developing the fraction-order memristor-based Lorenz system with a piecewise linear function arose. In this paper, we first propose a new fractional-order memristor-based Lorenz system with the flux-controlled memristor characterized by a piecewise linear function, and its dynamical behaviors are illustrated by using a phase portrait, a bifurcation diagram, the largest lyapunov exponent and a power spectrum diagram. Then, what happens if the memristor is replaced with a quadratic nonlinearity, a cubic nonlinearity and a quartic nonlinearity, respectively? This paper gives the answer. Simulation results show that these fractional-order memristor-based systems exhibit some interesting dynamical behaviors within a certain range of parameters.

The organization of this paper is as follows. In Section 2, some preliminaries of fractional calculus and memristors are briefly reviewed. Section 3 presents the generation of fractional-order memristor-based Lorenz systems with four different flux-controlled memristors. In addition, the nonlinear dynamical behaviors of the proposed systems are analyzed. The conclusions are finally drawn in Section 4.

2. Preliminaries

2.1. Grünwald-Letnikov Fractional Derivative

Given that the method defined by Grünwald-Letnikov (GL) is the most direct numerical one to solve the fractional calculus in the various definitions of derivative [23–25], in this work, the q-th-order GL definition is given by [23,24]:

$${}_{{\alpha }_0}{D}_t^{q}f(t)=\underset{t\to 0}{\lim }{h}^{-q}{\displaystyle \sum _{j=0}^{\frac{t-{\alpha }_0}{h}}{(-1)}^j\left(\begin{array}{c}q\\ j\end{array}\right)f(t-jh)}$$

(1)

where:

$$\left(\begin{array}{c}q\\ j\end{array}\right)=\frac{q(q-1)\cdots (q-j+1)}{j!}.$$

Equation (1) can be reduced to:

$${}_{{\alpha }_0}{D}_t^{q}y(k)=h^{-q}{\displaystyle \sum _{j=0}^k{\omega }_j^{(q)}{y}_{k-j},}$$

(2)

where:

$${\omega }_j^{(q)}={(-1)}^j\left(\begin{array}{c}q\\ j\end{array}\right),j=0,1,2,\cdots$$

and h is the time step.

2.2. Memristor Model

At present, many memristor models have been proposed in [1,26,27]. The memristor model used in this paper is a flux-controlled memristor model described by the following circuit equations:

$$\begin{array}{l}i=W(\phi )\upsilon ,\\ \frac{d\phi }{dt}=\upsilon ,W(\phi )=\frac{dq(\phi )}{d\phi },\end{array}$$

(3)

where i and υ denote the current through and the voltage across the device; q(φ) and W (φ) are called the memristance and the memductance, respectively [17].

3. Fractional-Order Memristor-Based Lorenz Systems

In this section, four new fractional-order memristor-based Lorenz systems are introduced. In order to compare the nonlinear dynamical properties of these four systems under the same order, q is taken as 0.996 in the following sections.

3.1. Fractional-Order Lorenz System with the Flux-Controlled Memristor Characterized by a Piecewise Linear Function

An integer-order memristor-based Lorenz system with the piecewise linear function is described by [22]:

$$\{\begin{array}{l}{\dot{x}}_1(t)=-a{x}_1(t)-W(x_4(t))x_1(t)+b{x}_2(t),\\ {\dot{x}}_2(t)=c{x}_1(t)-x_2(t)-x_1(t)x_3(t),\\ {\dot{x}}_3(t)=x_1(t)x_2(t)-d{x}_3(t),\\ {\dot{x}}_4(t)=-x_1(t),\end{array}$$

(4)

where q₁(x₄(t)) and W(x₄(t)) are given by:

$$q_1(x_4(t))=\rho x_4(t)+0.5(\sigma -\rho )(|x_4(t)+1|-|x_4(t)-1|),$$

(5)

$$W(x_4(t))=\frac{d{q}_1(x_4(t))}{d{x}_4(t)}=\{\begin{array}{c}\sigma ,|x_4(t)|\le 1,\\ \rho ,|x_4(t)|>1.\end{array}$$

(6)

The equations of the fractional-order memristor-based Lorenz system with the piecewise linear function are given by:

$$\{\begin{array}{l}{D}^q{x}_1(t)=-a_1{x}_1(t)-W_1(x_4(t))x_1(t)+b_1{x}_2(t),\\ D^q{x}_2(t)=c_1{x}_1(t)-x_2(t)-x_1(t)x_3(t),\\ D^q{x}_3(t)=x_1(t)x_2(t)-d_1{x}_3(t),\\ D^q{x}_4(t)=-x_1(t),\end{array}$$

(7)

where q is the fractional-order satisfying 0 < q < 1. W₁(x₄(t)) is the same as W (x₄(t)) in Equation (6).

The equations of System (7) are derived from the integer-order counterpart, but the value of system parameters of the original integer-order system cannot be applied to the fractional-order system directly. If the memristor is changed again to a quadratic nonlinearity, a cubic nonlinearity or a quartic nonlinearity memristance in the following sections, the choices of system parameters and the order q, which cause the systems to be of chaos, need a large amount of trial and error by numerical simulations and nonlinear dynamical analyses. In what follows, the nonlinear dynamical behaviors of System (7) are studied by a bifurcation diagram, the largest Lyapunov exponent, a phase portrait and a power spectrum diagram.

3.1.1. Bifurcation Analysis

Taking a₁ = 8, b₁ = 15, $d_1=\frac{8}{3}$, σ = 5, ρ = 8 and q = 0.996, and changing the value of c₁, the bifurcation diagram of System (7) when c₁ ∊ [15, 40] is shown in Figure 1.

The change of the system parameter can lead to the sudden emergence, disappearance or mergence of the chaotic attractor in nonlinear dynamical systems, that is, the catastrophe. The catastrophe phenomena are ubiquitous in nonlinear systems. When the system parameters are altered to a critical state, the dynamical behavior of the system will suddenly change. In Figure 1, by means of numerical simulations, we can come to the conclusion that the system first jumps from a stable focus when c₁ ∊ [15, 27.734] to a stable limit cycle when c₁ = 27.735, then from a stable limit cycle to an unstable focus when c₁ ∊ [27.736, 27.742], then from an unstable focus to chaos when c₁ ∊ [27.743, 40], with the increasing parameter c₁.

3.1.2. The Largest Lyapunov Exponent, Phase Portrait and Power Spectrum Analysis

When c₁ = 35, using the method determining the value range of q by the largest Lyapunov exponent in [28,29], the new 4D fractional-order System (7) is chaotic for 0.988 ≤ q < 1. When q = 0.996, the largest Lyapunov exponent is 0.0022; the time history, phase portrait and power spectrum diagram of the chaotic attractor are shown as Figure 2.

3.2. Fractional-Order Lorenz System with the Flux-Controlled Memristor Characterized by a Quadratic Nonlinearity

Based on the above-mentioned System (7), the piecewise linear function is replaced with a quadratic nonlinearity. Additionally, we can derive the equations of the fractional-order memristor-based Lorenz system with a quadratic nonlinearity from the integer-order counterpart [14]:

$$\{\begin{array}{l}{D}^q{y}_1(t)=-a_2{y}_1(t)-W_2(y_4(t))y_1(t)+b_2{y}_2(t),\\ D^q{y}_2(t)=c_2{y}_1(t)-y_2(t)-y_1(t)y_3(t),\\ D^q{y}_3(t)=y_1(t)y_2(t)-d_2{y}_3(t),\\ D^q{y}_4(t)=-y_1(t),\end{array}$$

(8)

where q₂(y₄(t)) and W₂(y₄(t)) are described by:

$$q_2(y_4(t))=-{\alpha }_1{y}_4(t)+0.5{\beta }_1{(y_4(t))}^2\mathit{sgn}(y_4(t)),$$

(9)

$$W_2(y_4(t))=\frac{d{q}_2(y_4(t))}{d{y}_4(t)}=-{\alpha }_1+{\beta }_1|y_4(t)|.$$

(10)

Similarly, we further investigate the nonlinear dynamical behaviors of System (8), including the bifurcation diagram, the largest Lyapunov exponent, phase portraits and power spectrum diagrams.

3.2.1. Bifurcation Analysis

Let a₂ = 3.9, b₂ = 10, $d_2=\frac{8}{3}$, α₁ = −0.7 × 10⁻³, β₁ = 0.03 × 10⁻³ and q = 0.996. Figure 3 shows the bifurcation diagram of System (8) when c₂ ∊ [20, 45]. The most interesting phenomenon is the existence of the inverse period-doubling bifurcation with the increasing of parameter c₂.

From Figure 3, we can obtain the following dynamical behaviors:

• System (8) undergoes the bifurcation from a stable focus to an unstable focus when c₂ ∊ [20, 21.641];
• The first inverse period-doubling bifurcation from chaos beginning at c₂ = 21.642 to the period-5 orbit when c₂ ∊ [34.59, 35.06]; the second inverse period-doubling bifurcation from chaos beginning at c₂ = 35.07 to the period-3 orbit when c₂ ∊ [35.96, 38.3]; the third inverse period-doubling bifurcation from chaos beginning at c₂ = 38.31 to the period-1 orbit when c₂ ∊ [41.22, 45];
• The occurrence of intermittent chaos.

3.2.2. The Largest Lyapunov Exponent, Phase Portraits and Power Spectrum Analysis

When c₂ = 30, we can determine that the new 4D fractional-order System (8) is chaotic for 0.992 ≤ q < 1 by the largest Lyapunov exponent. When q = 0.996, the largest Lyapunov exponent is 0.0239. Taking c₂ = 30, 34.89, 34.77 and 44.5, respectively, and the time histories, phase portraits and power spectrum diagrams of chaotic attractor, the period-5 orbit, period-3 orbit and period-1 orbit are shown in Figure 4a–d, respectively.

3.3. Fractional-Order Lorenz System with the Flux-Controlled Memristor Characterized by a Smooth Continuous Cubic Nonlinearity

Similarly, based on the above-mentioned System (7), the piecewise linear function is replaced with a cubic nonlinearity. Additionally, we can derive the equations of the fractional-order memristor-based Lorenz system with a cubic nonlinearity from the integer-order counterpart as [15–18]:

$$\{\begin{array}{l}{D}^q{z}_1(t)=-a_3{z}_1(t)-W_3(z_4(t))z_1(t)+b_3{z}_2(t),\\ D^q{z}_2(t)=c_3{z}_1(t)-z_2(t)-z_1(t)z_3(t),\\ D^q{z}_3(t)=z_1(t)z_2(t)-d_3{z}_3(t),\\ D^q{z}_4(t)=-z_1(t),\end{array}$$

(11)

where q₃(z₄(t)) and W₃(z₄(t)) are described by:

$$q_3(z_4(t))={\alpha }_2{z}_4(t)+{\beta }_2{(z_4(t))}^3,$$

(12)

$$W_3(z_4(t))=\frac{d{q}_3(z_4(t))}{d{z}_4(t)}={\alpha }_2+3{\beta }_2{(z_4(t))}^2.$$

(13)

Moreover, the dynamical behaviors of System (11) are investigated by the same means.

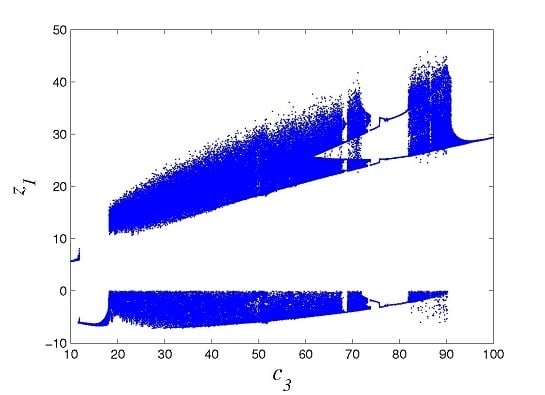
3.3.1. Bifurcation Analysis

Let a₃ = 8, b₃ = 11, $d_3=\frac{8}{3}$, α₂ = 0.67 × 10⁻³, β₂ = 0.02 × 10⁻³ and q = 0.996. The bifurcation diagram of System (11) when c₃ ∊ [10, 100] is demonstrated in Figure 5. The phenomenon of the inverse period-doubling bifurcation exists in System (11), as well.

From Figure 5, the dynamical behaviors are analyzed as follows:

• System (11) undergoes the bifurcation from a stable focus to an unstable focus when c₃ ∊ [10, 18.12];
• The first inverse period-doubling bifurcation from chaos beginning at c₃ = 18.121 to the period-5 orbit when c₃ ∊ [67.84, 68.95]; the second inverse period-doubling bifurcation from chaos beginning at c₃ = 68.96 to the period-3 orbit when c₃ ∊ [73.77, 81.9]; the third inverse period-doubling bifurcation from chaos beginning at c₃ = 81.91 to the period-1 orbit when c₃ ∊ [97.83, 100];
• The occurrence of intermittent chaos.

3.3.2. The Largest Lyapunov Exponent, Phase Portraits and Power Spectrum Analysis

When c₃ = 35, the order of the new 4D fractional-order System (11) appearing as chaos is 0.984 ≤ q < 1 by the largest Lyapunov exponent. When q = 0.996, the largest Lyapunov exponent is 0.0234; taking c₃ = 35, 68.88, 80 and 98, respectively. Figure 6a–d correspondingly shows time histories, phase portraits and power spectrum diagrams of chaotic attractor, period-5 orbit, period-3 orbit and period-1 orbit.

3.4. Fractional-Order Lorenz System with the Flux-Controlled Memristor Characterized by a Quartic Nonlinearity

In this section, according to the charge-controlled memristor characterized by a fourth degree polynomial function in [19], the memristor in System (7) is replaced with the new flux-controlled memristor characterized by a quartic nonlinearity. Additionally, we can get the following equations of the fractional-order memristor-based Lorenz system with a quartic nonlinearity as:

$$\{\begin{array}{l}{D}^q{w}_1(t)=-a_3{w}_1(t)-W_4(w_4(t))w_1(t)+b_3{w}_2(t),\\ D^q{w}_2(t)=c_3{w}_1(t)-w_2(t)-w_1(t)w_3(t),\\ D^q{w}_3(t)=w_1(t)w_2(t)-d_3{w}_3(t),\\ D^q{w}_4(t)=-w_1(t),\end{array}$$

(14)

where q₄(w₄(t)) and W₄(w₄(t)) are described by:

$$q_4(w_4(t))={\alpha }_3{(w_4(t))}^4\mathit{sgn}(w_4(t))+{\beta }_3{(w_4(t))}^2\mathit{sgn}(w_4(t))-{\gamma }_3,$$

(15)

$$W_4(w_4(t))=\frac{d{q}_4(w_4(t))}{d{w}_4(t)}=4{\alpha }_3|w_4(t){|}^3+2{\beta }_3|w_4(t)|.$$

(16)

Furthermore, the dynamical behaviors of System (14) are studied by the same means.

3.4.1. Bifurcation Analysis

Let a₄ = 6.4, b₄ = 15.5, d₄ = 3.1, α₃ = 0.63 × 10⁻³, β₃ = 0.025 × 10⁻³ and q = 0.996. The bifurcation diagram of System (14) when c₄ ∊ [14.32, 55] is shown in Figure 7.

By numerical simulations, the dynamical behaviors are analyzed as follows:

• System (14) goes through the bifurcation from focus beginning at c₄ = 14.32 to chaos beginning at c₄ = 18.41;
• The first inverse period-doubling bifurcation from chaos beginning at c₄ = 18.41 to the period-3 orbit when c₄ ∊ [33.69, 34.09]; the first quasi-period beginning at c₄ = 34.1 to the period-3 orbit when c₄ ∊ [35.6, 37.69]; the second inverse period-doubling bifurcation from chaos beginning at c₄ = 37.7 to the second quasi-period when c₄ ∊ [42.175, 42.37] to the period-1 orbit when c₄ ∊ [42.38, 55];
• The occurrence of intermittent chaos.

3.4.2. The Largest Lyapunov Exponent, Phase Portraits and Power Spectrum Analysis

When c₄ = 26, we can obtain that the new System (14) is chaotic for 0.984 ≤ q < 1 by the largest Lyapunov exponent. When q = 0.996, the largest Lyapunov exponent is 0.0174; taking c₄ = 26, 33.92, 34.2, 37.27, 42.2 and 54, respectively. Figure 8a–f correspondingly shows time histories, phase portraits and power spectrum diagrams of chaotic attractor, period-3 orbit, quasi-period orbit and period-1 orbit.

4. Conclusions

This paper introduced fractional-order memristor-based Lorenz systems with the flux-controlled memristor characterized by a piecewise linear function, a quadratic nonlinearity, a cubic nonlinearity and a quartic nonlinearity, respectively. Additionally, some interesting dynamical behaviors of these four systems are further demonstrated by computer simulations, including phase portraits, bifurcation diagrams, the largest Lyapunov exponent and power spectrum diagrams. Simulation results show that the introduction of a memristor leads to more complicated dynamical behaviors. We will provide a more detailed analysis in the next step. In addition, designing the new combination synchronization scheme for these four systems and constructing the fractional-order memristor-based Lorenz systems with a fifth or higher degree polynomial memristor will be our future work.