1. Introduction
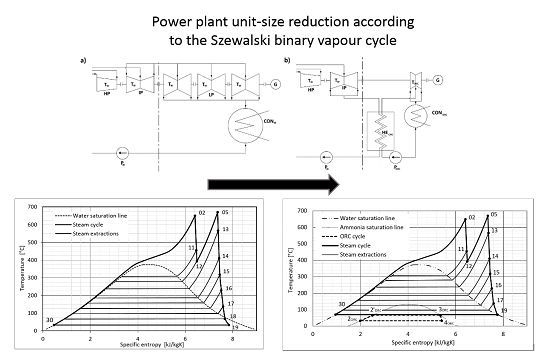
In the 1960s, Robert Szewalski introduced a binary vapor cycle consisting of a supercritical steam cycle and an organic Rankine cycle (ORC) coupled in a hierarchical energy system. The purpose of this idea was to facilitate the design of power units producing a few gigawatts of power.
Here, we present the generally accepted terms and common parts of the binary cycle and ORC. We next discuss the primary differences between typical binary cycles and the Szewalski cycle, and we explain the Szewalski cycle in particular. We note that the entire system consists of a traditional steam cycle and the ORC. The Szewalski binary vapor cycle [
1,
2] uses steam as a working fluid in the high-temperature part of the cycle; another fluid—an organic working fluid with a low specific volume—is used as a working substance that takes the place of conventional steam over a range of temperatures represented by low-pressure (LP) steam expansion (
Figure 1).
Figure 1.
Scheme of the Szewalski binary vapor concept cycle (b) compared with the conventional supercritical steam cycle (a). LP—low-, IP—intermediate-, and HP—high-pressure part of the steam turbine. HEORC—regenerative heat exchangers, PW—water pump, G—generator, CONW—condenser of water steam, TW—steam turbine, TORC—turbine of low-boiling point fluid, PORC—pump of low-boiling point fluid, CONORC—condenser of vapor of low-boiling point fluid.
Figure 1.
Scheme of the Szewalski binary vapor concept cycle (b) compared with the conventional supercritical steam cycle (a). LP—low-, IP—intermediate-, and HP—high-pressure part of the steam turbine. HEORC—regenerative heat exchangers, PW—water pump, G—generator, CONW—condenser of water steam, TW—steam turbine, TORC—turbine of low-boiling point fluid, PORC—pump of low-boiling point fluid, CONORC—condenser of vapor of low-boiling point fluid.
The binary vapor cycle is a thermodynamic cycle that converts thermal into mechanical energy. It is composed of two sub-cycles that employ two different working fluids. The most common applications include serial coupling of sub-cycles, but a parallel configuration is also possible [
3,
4]. Binary sets have been well known since the beginning of the 20th century. A mercury-steam cycle was introduced to improve the steam cycle efficiency by increasing the working fluid’s temperature without increasing its pressure [
1,
2], which is consistent with the theory of the Carnot heat engine efficiency [
5]. The development of material science and production technology has led to complex and expensive binary sets being replaced by steam sets with live steam parameters of 550 °C and 15 MPa or higher [
6,
7].
However, the importance of the binary cycle increases in the low-temperature range—for example in geothermal power engineering. In geothermal power plants, the first working fluid was geothermal water or steam that only heated the second fluid (
i.e., pure steam in a closed steam turbine cycle) [
8]. The goal of this methodology was to separate the turbines from water containing mineral inclusions. However, for the last three decades, geothermal power plants have been intensively developing low-boiling point fluids. ORCs can use low-temperature geothermal heat sources because of their low operating temperatures. Hence, they attain a low thermodynamic efficiency typically in the range of 0.08–0.12 [
8,
9].
The low thermodynamic efficiency of ORCs does not mean that they cannot be effectively used to generate electricity. ORCs usually attain high exergetic efficiencies that are comparable to the efficiency of steam cycles, without taking boilers into account. Secondly, due to a cascade application it is possible to couple an ORC with a conventional Rankine cycle or to another ORC in very efficient applications by optimally matching the cycle thermodynamic parameters to the heat source and sink. In this case, the condenser of one sub-cycle is simultaneously an evaporator of the next one [
3,
8,
10,
11]. More so, the application of low-boiling point fluids in energy cycles is associated with advantages other than the utilization of low-temperature heat sources [
11]. One of these advantages is employed in the Szewalski binary vapor cycle.
Studies and a patent by Szewalski [
1,
2] operate on a specific assumption, which is presented below. According to Szewalski, a supercritical steam cycle is preferred due to its high efficiency in the primary part of the cycle. In the second part of the cycle, the ORC provides a working fluid with a low specific volume. The objective of this concept is to significantly reduce the LP turbine sizes and hence make it possible to increase the output power attainable by a single turbine unit [
1,
2]. This process leads to an increased gross efficiency of the power plant gross and a decreased specific investment and maintenance costs [
1,
2,
12].
The low specific volume of the LP turbine outlet steam in condensing power plants leads to an increase in the demand for materials. The cylinder of the LP turbine, in units of approximately 600 MW
e of output power and above, is typically divided into three parallel casings in which the last-stage blades are limited to approximately one meter [
7]. Moreover, because steam starts to condensate at the last stages of the LP turbine, very expensive materials are required to prevent corrosion and erosion and to withstand the large mechanical stresses. For instance, the LP part of a conventional turbine-unit with about 600 MW
e with three double-flow low LP cylinders (casings) has an output of approximately one third of the entire set up; its initial cost is in the order of two thirds of that of the entire unit. If we can decrease the cost of this part that now includes the cold vapor turbine and the heat exchanger to one half of the cost of the conventional design, then the cost of the entire unit will be only two thirds of the previous cost. This decrease is significant given that the economic considerations are tied to real technical progress [
1]. A scheme of the size reduction is presented in
Figure 1.
The most recent analysis of thermodynamic and operational parameters of the Szewalski binary vapor cycle was performed by Ziółkowski
et al. [
7]. This analysis was carried out using accessible numerical Computational Flow Mechanics (CFM) codes via step-by-step modeling of separate apparatuses. In the Szewalski binary vapor cycle, we considered four potential working fluids (propane, isobutene, ethanol and ammonia) to obtain the highest output and a First Law efficiency of the cycle.
Another supercritical steam cycle that utilizes an ORC cycle has been analyzed in the literature [
13,
14]. The objective of these studies was to analyze the thermodynamic and operational parameters of a supercritical power plant given reference conditions; this research also focused on the introduction of a hybrid system incorporating an ORC. In an ORC, the upper heat source is a stream of hot water from the system of heat recovery with a temperature of 90 °C, which is additionally aided by heat from steam bleeds of the LP steam turbine. Ziółkowski
et al., conducted a thermodynamic analysis of the supercritical plant with and without incorporation of the ORC using CFM numerical codes. Four fluids (propane, isobutane, pentane and ethanol) were investigated in [
13], and six working fluids (propane, isobutane, pentane, ethanol, R236ea and R245fa) were investigated in [
14]. In the course of the calculations, it was determined that the unit power increased and that a First Law efficiency was attained for the reference case and the case with the ORC.
An analysis of literature results [
7,
13,
14,
15,
16,
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32,
33,
34] pertaining to exergy confirms that good resolution is to perform the exergy loss analysis in the Szewalski cycle.
Exergy analysis is an important tool for the optimization of complex thermodynamic processes because energy balance alone does not include entropy generation and therefore energy quality degradation. For technical and economic reasons, the quality of energy is closely related to investment and maintenance costs [
16,
17,
18]. It should be noted that a First Law analysis is not only incomplete but also misleading because it distorts the real resource consumption quantifiers and overestimates low-exergy (high-entropy) fluxes [
17].
A good example of an exergy analysis of a power cycle is [
19], in which the authors present an original and rapid method for heat recovery steam generator (HRSG) exergetic optimization. The main aim of the analysis is to maximize exergy transfer to the water/steam cycle. The proposed approach fixes the pinch point and the economics by imposing the total heat transfer area of the HRSG. In another study [
20], the author proposes reconsidering direct and inverse configurations of Carnot machines, and he presents two examples. The first example is concerned with a “thermofrigo-pump” in which the two utilities are hot and cold thermal exergies due to the difference in the temperature level compared with the ambient temperature. The second example is relative to a “combined heat and power” (CHP) system [
20].
It should be noted that due to environmental-impact considerations and energy-conversion efficiency, the renewal and development of heat pumps and CHP systems has been increasing from large- to micro-scale systems (μCHP) for industrial, building applications and even photovoltaic/thermal (PV/T) configurations or fuel cell CHP systems [
17,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30,
31,
32]. Energy and exergy analyses have been conducted by many authors, for example: (1) a combined heat and power system by Feidt & Costea [
28]; (2) a novel hybrid solar heating, cooling and power generation system for remote areas by Zhai
et al. [
22]; (3) a combined molten carbonate fuel cell-gas turbine system by El-Emam & Dincer [
25]; (4) a comparison of Proton Exchange Membrane Fuel Cell and Solid Oxide Fuel Cell-based μCHP systems by Barelli
et al. [
27]. Additionally, exergy analyses of poly-generation systems for sustainable building applications were conducted by Bingöl
et al. [
26]. Nieminen & Dincer [
24] compared gasoline and hydrogen fuelled internal combustion engines using exergy analyses. A review of exergo-economic analysis and optimization of combined heat and power production was performed by Abusoglu & Kanoglu [
23].
An exergy analysis offers useful insights into the correct assessment of the process itself: It identifies and quantifies the sources of irreversibility and allows for an immediate comparison of different process structures. Furthermore, such an analysis provides a clear indication for the resource-to-end-use matching, thus enabling better resource allocation. Its inability to account for externalities limits its usefulness in a broader context, however. Additionally, extended exergy analysis overcomes this latter limitation and provides a complete picture of how the process interacts with the biosphere and with the societal environment [
31].
According to Szargut’s proposal [
33], exergy is an adequate measure of the quality of natural resources. A complete example concerning the analysis of thermo-ecological cost has been presented in [
32]. These authors focus on an ecological analysis of coal injection as auxiliary fuel to the Tuyere zone of a blast furnace. Connections with coalmines, coke-oven batteries and power plants have been considered. The summary of Szargut’s investigations on this subject has been presented in [
33]. In a recent work, Ziębik and Gładysz [
34] presented an algorithm for calculating the thermo-ecological costs of an integrated oxy-fuel combustion power plant based on an “input-output” model of direct energy and material consumption and also on the application of an “input-output” approach for the construction of a mathematical model of the thermo-ecological costs of such a power plant. In order to construct this model, the authors assumed that interconnections between the analyzed integrated oxy-fuel combustion power plant and domestic economy were rather weak, which permitted them to establish indices of thermo-ecological costs concerning fuels, raw materials and semi-products on the basis of
a priori knowledge [
34]. However, the thermo-ecological optimization of a solar collector was also established [
30].
Exergy is a suitable measure of differences in the environment. Various authors have examined the concept of sustainability in relation to exergy flows on Earth. Exergy is applied to emissions into the environment using case studies in order to describe and evaluate its values and limitations as an ecological indicator. Exergy has also been considered to be a useful ecological indicator according to the literature [
35].
Exergy accounting has been successfully used for diagnosing energy systems and for accounting for the Earth’s exergy resources. Both applications rely on the concept of exergetic cost. This concept attempts to measure the amount of exergy resources necessary to produce any effect. The process of cost formation becomes essential to understanding and evaluating exergy costs and the degradation process of resources feeding a system. Cost, irreversibility and causation become deeply interrelated, and an Aristotelic analogy between cause and thermo-economic concepts is highlighted [
36].
Besides applications to “systems engineering”, another area in which exergy analysis is of importance is the allocation of funding for research and development, irrespective of whether the funding is corporate, entrepreneurial or governmental. Furthermore, exergy analysis can be used for establishing policies [
17,
37].
From an economical point of view, the construction of powerful steam turbine sets is desirable. First of all, due to the increase in machinery output power (steam boilers, feed water pumps, turbines, even the size of power plant halls), specific investment costs are decreasing. Secondly, machinery efficiency is always higher for large applications [
1,
2,
6,
7]. Moreover, maintenance costs such as the number of power plant staff, logistics, renovations, diagnostics,
etc., are also relatively lower for larger applications.
Here, we present a Szewalski binary vapor cycle exergy loss analysis. However, in order to present the issue correctly our analysis is based on meaningful values using power plant data [
7,
13,
14]. Our methodology consists of the following steps:
- -
The creation of a steam cycle mathematical model convergent with a supercritical power plant cycle;
- -
The choice of optimal parameters for the “cut-off” LP steam turbine;
- -
The optimization of the ORC thermodynamic parameters;
- -
The selection of the low-boiling point working fluid for the ORC installation;
- -
A comparison of exergy losses in the reference cycle and the Szewalski cycle using collected data;
- -
A summary and conclusion.
2. Referent Model of a Supercritical Steam Cycle
Our analysis of the exergy losses in a binary vapor cycle is based on a CFM model of supercritical steam power, which we refer to as a reference model. The thermodynamic cycle consists of a steam boiler (B) with a steam superheater and re-heater, a three-cylinder (casing) steam turbine (HP, IP, SP) with an electric generator (G), a condenser (CON) and a feed water regeneration system (HE1–HE8) with a deaerator (D).
The thermodynamic parameters of the reference model have been validated using literature data [
7,
14]. The most significant difference between the reference model and literature data is a steam turbine output power lower by about 510 kW,
i.e., 899,490 kW for the reference model and 900,000 kW for a real cycle. A list of the most important cycle parameters and assumptions can be found in the appendix (
Supplementary data—Table S1). A full list of the reference model thermodynamic parameters, according to
Figure 2, is presented in the appendix (
Supplementary data—Table S2). A correct and convergent mathematical model was the basis for our entire analysis.
Figure 2.
Thermodynamic scheme of the supercritical steam power plant-reference model: B—steam boiler with superheater, HP—high-pressure steam turbine, IP—intermediate-pressure steam turbine, LP—LP steam turbine, P—water pumps, CON—condenser, D—deaerator, G—electric generator, HE—regeneration heat exchangers.
Figure 2.
Thermodynamic scheme of the supercritical steam power plant-reference model: B—steam boiler with superheater, HP—high-pressure steam turbine, IP—intermediate-pressure steam turbine, LP—LP steam turbine, P—water pumps, CON—condenser, D—deaerator, G—electric generator, HE—regeneration heat exchangers.
In order to more clearly show the heat transfer and steam expansion phenomena occurring in the reference model devices, a temperature-specific entropy diagram is shown in
Figure 3. The characteristic points of the thermodynamic cycle are labeled the same as in
Figure 2. Bold lines indicate the main thermodynamic cycle, thin lines indicate steam extractions and their condensation temperatures and dashed line indicates the water saturation line.
Figure 3.
Characteristic thermodynamic points of the reference model represented in a temperature-specific entropy diagram.
Figure 3.
Characteristic thermodynamic points of the reference model represented in a temperature-specific entropy diagram.
The steam expansion from point 18 to 19 occurs with a lower efficiency than in other parts of the turbine for two reasons. The steam turbine reaches a lower isentropic efficiency during expansion in the range of wet steam. This phenomenon is complex, but, according to Baumann [
38], we can simplify the situation and assume that only the gas fraction in the wet steam flow expands and that the liquid fraction is responsible for the flow losses. More accurate explanations, according to Bakhtar
et al., and Gyarmathy and Lesch [
39,
40], involve local subcooling of the steam around the condensation germ. Moreover, the last turbine stage in condensing power plant is designed with some modifications in order to provide a safe working range of wet stem expansion, particularly under partial loads. Therefore, those improvements decrease the efficiency of the design point [
38]. Hence the next step is the choice of the optimal parameters for the “cut-off” LP steam turbine.
4. Exergy Balance
To conduct a reliable analysis of a thermodynamic cycle, particularly a complex hierarchical cycle, exergy analysis in addition to thermodynamic analysis is recommended [
43,
44,
45]. Exergy analysis yields a value of efficiency related to the “available energy” that can be converted into work [
45,
46]. The main feature of exergy is the usage of the thermodynamic temperature, which involves entropy generation. In this case, the ideal Carnot cycle always reaches 100% efficiency, and it shows if the analyzed cycle is closer to or further from the Carnot cycle efficiency [
43,
44]. Moreover, due to the analysis of exergy losses in the cycle it is possible to undertake proper optimization steps in selected devices to improve technical processes. Exergy analysis is particularly helpful for heat-transfer processes.
To begin the exergy analysis, we describe the exergy stream
according to [
44] as a sum of a usable part of the internal and external streams of energy:
where
describe the potential and kinetic streams of energy, respectively, and
is a thermal exergy stream consisting of two elements:
The e element describes the stream of physical exergy, which includes pressure and thermal exergy stream differences between the substance thermodynamic state and ambient parameters. The parameter describes the chemical energy of the substance assuming ambient temperature and pressure.
Narrowing down our considerations to fluid-flow machinery with adiabatic insulation from the environment, we can assume that the maximal technical work of the machinery is equal to the thermal exergy decrease of the thermodynamic fluid, which can be written as:
where
are the inlet and outlet enthalpy streams of the process, respectively, and
is the amount of useless heat exchanged with the environment.
According to the entropy definition from the Second Law of thermodynamics, the thermal exergy decrease can be described as:
where
is the ambient temperature and
are the inlet and outlet entropy streams, respectively.
However, if the chemical energy conversion of fuel in the combustion chamber, boiler or fuel cell is taken into consideration, Equation (6) must be applied to the stream of physical energy
and then Equation (4) becomes:
The procedure for evaluating the chemical exergy depends on the type of the reaction and the substrates. A complete procedure for a combustion process is presented in [
43,
44].
To close the exergy balance of the thermodynamic process, it is necessary to define the exergy losses. To illustrate the balance equations, a model of a thermal engine is presented in
Figure 11.
The proposed engine, a binary vapor cycle in this case, using a stream of thermal energy yields a stream of mechanical work and exhales a stream of worthless thermal energy . Additionally, coolant with an inflow stream enthalpy and entropy is heated to parameters ,
Figure 11.
Model of a thermal engine.
Figure 11.
Model of a thermal engine.
In general, the stream of exergy losses in machinery can be defined using an energy balance equation of real and ideal processes, respectively:
Using real and ideal processes and the stream of work definition based on Equations (8) and (9), the stream of exergy loss is defined as the difference between ideal process and real process streams of work, or stream of waste energy from real and ideal processes:
According to the Second Law of thermodynamics, the sum of the entropy streams in a system is more than 0, and the stream of entropy generation during a process can be described as:
In the ideal process, the sum of entropy streams equals 0:
By subtracting Equation (11) from Equation (12), we obtain:
Furthermore, by inserting Equation (13) into Equation (10), we can define the stream of exergy losses as the Gouy–Stodola law [
43,
44]:
To analyze the share of each machine in the cycle relative exergy losses, it is useful to employ the proportion of the exergy losses in the cycle driving exergy as a mass flow rate of the fuel and unit fuel exergy [
43,
44]:
where
is the fuel mass flow rate,
bFuel is the specific fuel exergy and
is the stream of exergy losses.
For example, the relative exergy losses in a model of a one-cylinder steam turbine and electric generator set ξ
T-G are given by:
The same losses for a steam condenser are given by:
where
is the steam mass flow rate,
is the turbine mechanical efficiency,
is the electric generator mechanical and electrical efficiency,
is the dryness fraction of the turbine outlet steam,
is the specific evaporation heat,
is the steam absolute temperature,
are the steam and condensate specific entropy, respectively,
are the steam and condensate specific enthalpy, respectively and
are the steam and condensate specific exergy, respectively.
The most general and the simplest formula for the exergetic efficiency refers to the ratio of the driving exergy
BD,s of a reversible ideal thermodynamic process to the driving exergy of a real process
BD [
43,
44]:
In Equation (18), one can see that the ideal Carnot cycle attains an exergetic efficiency of 100%, which is why, in general, the exergetic efficiency of thermodynamic cycles can be viewed as a fraction of the Carnot ideal cycle. A more accurate equation depends on the kind of physical process or, in case of the thermodynamic cycle, on the complexity of the cycle. For instance, the gross exergy efficiency of a steam boiler Equation (19) and the exergy efficiency of a pump Equation (20) can be given as:
where
is the pump mechanical efficiency,
is the pump internal efficiency and
is the pumped media mean absolute temperature.
Equation (19) can be used to determine the exergetic efficiency of a heat exchanger by measuring the change of the mass stream and specific exergy of fuel in a heating media mass stream and the specific exergy difference at the inlet and outlet of the heat exchanger. The exergetic efficiency of a more complex model of real machinery or a thermodynamic system can be easily estimated via a balance of losses:
where the index
i is the number of machines.
For a simple model of the Clausius–Rankine cycle, the exergy balance is given as follows:
A Comparison of Exergy Losses in Considered Cycles
In the present case in which the ORC installation is added to a supercritical steam cycle, we propose to perform the exergy analyses only for the added devices to investigate their impact on the entire cycle. This line of reasoning for the optimization analysis is used to minimize the costs of implementing the Szewalski idea in a supercritical power plant. Secondly, the steam cycle is already optimized, and changing its parameters is undesirable. The steam cycle parameters were changed between the LP turbine second steam extraction (point 17 in
Figure 5) and the regeneration heat exchanger HE2. The results of simplified exergy analyses of the reference cycle machinery and their equivalent machinery in the Szewalski cycle are presented in
Table 2.
Table 2.
Impact of the Szewalski cycle modernization on the reference cycle based on exergy loss analysis for the chosen cycle devices following the nomenclature of
Figure 2 and
Figure 5.
Table 2.
Impact of the Szewalski cycle modernization on the reference cycle based on exergy loss analysis for the chosen cycle devices following the nomenclature of Figure 2 and Figure 5.
| Devices | Type Value | Exergy Analysis |
|---|
| Reference Cycle | Szewalski Cycle | Reference Cycle | Szewalski Cycle |
|---|
| LP | LP* + TORC | | 0.02 | 0.02 |
| CON | CONORC | | 0.03 | 0.04 |
| HE1 | HEORC | | <0.01 | <0.01 |
| 0.71 | 0.89 |
| HE2 | HE2* | | <0.01 | <0.01 |
| 87 | 0.84 |
| - | PORC | | - | <0.01 |
| - | 0.87 |
The values in
Table 2 were calculated according to the equation for the exergy balance. The main assumptions, such as fuel exergy for hard coal, condensation exergy, steam exergy, etc were assumed based on the literature data [
33]. Further parameters for calculation, such as temperature, mass flow rate, specific enthalpy,
etc., are shown in
Supplementary data—Table S2.
The exergy analysis reveals that the replacement of one LP steam turbine by a smaller LP* steam turbine and a TORC turbine does not increase the exergy losses because the internal efficiency and enthalpy drops are nearly the same in both cycles. Moreover, the “external” thermodynamic parameters for LP and LP* + TORC are constant. The slight increase in the related exergy losses in the ORC condenser (CONORC), even though the same thermodynamic efficiency is employed in both cycles, is caused by an increase of condensation temperature and the removal of one steam extraction and regeneration steam exchanger. This increase of temperature and the removal lead to an increase of heat injected into the condenser, which causes higher related losses. The next modification concerns the replacement of the regeneration heat exchanger HE1 by the ORC vapor generator (HEORC). In both cycles for the presented thermodynamic configuration these devices have no significant influence on the exergy losses of the cycles. However, if the LP turbine “cut-off” point is selected for higher steam parameters to further reduce the size of the LP turbine, then the exergy efficiency decreases, and the related exergy losses will be more significant.
The device that was not changed was heat exchanger HE2. Its thermodynamic parameters, however, were changed. When the low temperature regeneration system was changed, the role of the heat exchanger HE2* was to compensate the difference in the Szewalski cycle. We assumed that the cycle parameters after the HE2 would be the same for both presented cycles. To demonstrate the subtle changes in the exergy balance of presented cycles, the exergy efficiency
. of heat exchangers and ORC pump have been added to
Table 2. It should be noted that in both cycles the energy efficiency of the heat exchangers is assumed to be 99.5%. Such a large difference between the energy and exergy efficiency results from entropy generation, which is taken into account in the exergy balance.
A device that has been added to the Szewalski cycle, but has no equivalent in the reference model, is the ORC pump. Through its high internal and exergy efficiency it can have a significant impact on related exergy losses, the net electric cycle output power and the net efficiency. In the configuration of thermodynamic parameters that we present, these losses are very low. However, increasing the pressure ratio in the ORC cycle increases the role of the pump in the balance. This situation occurs when higher thermodynamic parameters of the ORC cycle are adopted. Then, in order to provide a proper temperature for the evaporation of the working fluid, the pressure in the heat exchanger needs to be increased. Superheated ammonia vapor is recommended only in cases in which superheated steam is used to supply the HE
ORC exchanger to optimize the heat transfer. A different pressure ratio in the ORC installation can also occur for different working fluids. For instance, as shown in
Figure 7, the model that we investigated for each low-boiling point fluid generated almost the same amount of electricity at the optimal point. This result occurs because the exergy losses in all devices are minimalized and are almost the same. However, the electric net power is different for each fluid. This difference is caused by the different pressure ratios in the cycle for each low-boiling point fluid, which also accounts for the differing pump power demands. A decreased pressure ratio is recovered for ethanol, ammonia, isobutane and propane, in that order, which is consistent with the diagram shown in
Figure 7. Changes in the power demand of the condensate pump, P in
Figure 2 and
Figure 5, in the analyzed cycles was negligible.
5. Conclusions
Our analysis has revealed that the Szewalski binary vapor cycle has a great potential in the field of reducing the size of power units. Such a reduction can be used particularly for designing units with a large output power, which is desirable for the many technical and economic reasons noted in this manuscript. Unfortunately, the binary cycle is associated with some energy losses and a slight decrease in energy efficiency relative to a single steam cycle. However, installing an ORC provides a significant opportunity to utilize waste heat expelled from the power plant machinery.
For our analyses, ammonia was chosen as the working fluid for several reasons. Ammonia yields the largest reduction in the size of the turbine exhaust channels: Roughly a factor of 10 compared with the reference LP steam turbine. Secondly, ammonia is associated with nearly the highest electric net efficiency of the cycle. The most significant reduction in the cycle electric net power is caused by the power demands of the ORC pump. In the case of ammonia, the pump power demand is higher than that of ethanol but smaller than that of isobutane or pentane. This situation persists because the pressure difference due to the evaporation and condensation temperatures is higher for ammonia than for ethanol and smaller than that of the other tested fluids. Moreover, ammonia used as a wet fluid should be superheated prior to entering the turbine inlet. However, due to the small temperature difference between the generated steam and the condensation point, the vapor dryness fraction at the outlet of the ORC turbine is the same as in the case of the LP steam turbine in the reference cycle (i.e., approximately 0.93).
The thermodynamic configuration of the cycle that we present here is the result of an optimization process. Thanks to this optimization process the heat exchangers, which play a key role in the hierarchical cycles, do not cause a large entropy generation, which thereby prevents significant exergy losses. Exergy analysis is an important tool for the optimization of complex thermodynamic processes because the energy balance does not include entropy generation and, therefore, energy quality degradation. For technical and economic reasons, the quality of energy is closely related to initial and ongoing maintenance costs. For these reasons, temperature and entropy are energy conversion phenomena that are coupled in the exergy balance; they cannot be omitted in the process of design and optimization, particularly when the temperatures of the hot and cold reservoirs are set (e.g., in binary vapor cycles, gas-steam cycles or in low-temperature waste heat recovery systems). For heat-transfer processes such as combustion, mixing or heat exchanging, exergy analysis is particularly recommended because it is a measure of process irreversibility.
Throughout the exergy analysis, little difference between the reference cycle and the Szewalski cycle can be observed. From the values in
Table 2, it can be seen that the related exergy losses increase by about 1% in the case of the Szewalski cycle.
The remaining parts of the cycle were not taken into consideration (using exergetic analysis) because no changes were observed. Therefore, we can conclude that the exergy losses also remain the same. Using this line of reasoning, we could analyze the impact of the Szewalski “modernization” on the exergetic efficiency. In this case, exergetic analysis of the entire cycle was not necessary.
On the other hand, the thermodynamic analysis (First Law) revealed that the reference cycle with an efficiency of 47.58% was more efficient from an energy balance standpoint. Energy efficiency of the Szewalski cycle was lower by 0.19%.
However, it should be noted that the authors are also planning to conduct the thermoecological and thermoeconomic analyses as they were included in the work [
30,
32,
33].
The authors suggest that when using the waste heat stream, the exhaust gas amongst others, the Szewalski cycle can raise the efficiency of the supercritical block (both increase the net efficiency and reduce exergy losses).