Entropy Analysis of Solar Two-Step Thermochemical Cycles for Water and Carbon Dioxide Splitting

Abstract

The present study provides a thermodynamic analysis of solar thermochemical cycles for splitting of H₂O or CO₂. Such cycles, powered by concentrated solar energy, have the potential to produce fuels in a sustainable way. We extend a previous study on the thermodynamics of water splitting by also taking into account CO₂ splitting and the influence of the solar absorption efficiency. Based on this purely thermodynamic approach, efficiency trends are discussed. The comprehensive and vivid representation in T-S diagrams provides researchers in this field with the required theoretical background to improve process development. Furthermore, results about the required entropy change in the used redox materials can be used as a guideline for material developers. The results show that CO₂ splitting is advantageous at higher temperature levels, while water splitting is more feasible at lower temperature levels, as it benefits from a great entropy change during the splitting step.

1. Introduction

Fossil fuel depletion and the ongoing climate change lead to the need for a sustainable energy system. One important pillar of an energy system is the availability of fuels. Today, almost all fuels consumed worldwide are based on petroleum or natural gas, i.e., our mobility relies on unsustainable raw materials.

In order to improve this situation in the future, great research effort is put into the production of sustainable fuels, mainly hydrogen and synthetic hydrocarbons. One possible way to produce hydrogen and carbon monoxide is to apply solar-driven thermochemical cycles for water splitting or CO₂ splitting. The obtained gases can be either used directly as a fuel or further processed in a Fischer–Tropsch plant to generate synthetic hydrocarbons. Many thermochemical cycles have been investigated and evaluated in the past [1,2,3,4]. The cycle which is subject to most research activities in this area today is the two-step cycle based on a redox reaction as follows [5]:

• Endothermic reduction of a metal oxide (MO):

  MO_x → MO_x-δ + δ/2 O₂

  (1)
• Splitting step (for H₂O or CO₂)

  MO_x-δ + CO₂ → MO_x + δ CO

  (2)

  MO_x-δ + H₂O → MO_x + δ H₂

  (3)

Several thermodynamic evaluations of these cycles, especially the water-splitting cycle have been conducted [6,7,8,9]. In our group, we intend to revive the thermodynamic analysis of these cycles in a different way, based on vivid graphical representation. Further, we extend the existing work by analyzing the thermodynamic exigencies for different process parameters (temperatures, pressures). This way, we obtain the maximum efficiency as well as the required entropy change which the material needs to undergo. In a previous publication [10], we presented the methodology of the analysis based on T-S diagram representation. The work was limited to the water-splitting process and the influence of the solar efficiency was not taken into account. The present paper extends the analysis by considering also CO₂ splitting and comparing it to water splitting. Further, the solar efficiency is discussed and its influence on the theoretical process efficiency is presented.

2. One-Step Cycle and Solar Efficiency

2.1. Direct Gas Splitting—Thermolysis

In reality, direct splitting of water and CO₂ is not as trivial as presented in this paragraph. However, for the relevant temperature range this representation is sufficient, especially because the present section has an explanatory purpose only. In order to completely split water at 1 bar into oxygen and hydrogen, a temperature of about 4315 K is necessary. This high temperature is a result of the large enthalpy of formation of water and the low entropy change between H₂O and the product gases H₂ and O₂. The T-S representation of one-step water splitting and subsequent recombination at ambient temperature is shown in Figure 1. The entropy values shown here and in all subsequent figures in this paper are temperature-dependent and were generated with the thermochemistry software FactSage [11,12].

Figure 1. T-S diagram of one step splitting of 1 mol H₂O/CO₂ at 1 bar and 100% conversion.

Figure 1. T-S diagram of one step splitting of 1 mol H₂O/CO₂ at 1 bar and 100% conversion.

The water-splitting curve in Figure 1 encloses an area which represents the energy of formation of water (237 kJ/mol_H2O). This energy could be extracted from all water-splitting cycles, for example by recombining hydrogen and oxygen in an ideal fuel cell. In addition to the water-splitting cycle, Figure 1 also shows the simplified T-S representation of direct CO₂ splitting. Comparing the two cycles, CO₂ splitting seems to be more feasible, because the maximum process temperature is lower. The larger entropy change in the case of CO₂ splitting leads to an increased width of the enclosed area. Thus, the upper temperature being 3346 K is lower compared to H₂O splitting. This is the case, although the Gibbs free energy change is larger for CO₂ splitting (257 kJ/mol_CO), resulting in a larger enclosed area in Figure 1.

Due to the high process temperatures, the theoretical efficiency of direct splitting processes is high. The splitting-cycle efficiency η_sc is based on the net heat input ${\dot{Q}}_{NET}$ assuming ideal heat recovery. This heat recovery is the result of a pinch-point analysis with minimum temperature difference of 0 K. Such ideal heat recovery is assumed for all processes throughout this publication. In the case of water splitting, the enumerator in the efficiency formulation is the Gibbs free energy of formation of water ΔG_f,H2O. In the case of CO₂ splitting, the benefit is (ΔG_f,CO2 − ΔG_f,CO). This leads to the general form:

$${\eta }_{sc}=\frac{\mathsf{\Delta }{G}_f}{{\dot{Q}}_{NET}}$$

(4)

The efficiency of direct CO₂ splitting (η_sc = 90.6%) is advantageous compared to the efficiency of direct water splitting (n_sc = 82.8%). This advantage is due to the fact that the evaporation of water takes place at a low temperature. Such a low temperature input to a process decreases its efficiency.

2.2. Solar Absorption Efficiency

The solar absorption efficiency describes to which extent the solar radiation reaching the receiver can be used by a coupled process as thermal energy. It is strongly dependent on the receiver temperature and the concentration ratio C [13]. The concentration ratio describes the ratio between the collector aperture area and the absorber aperture area. Rising the receiver temperature as well as lowering the concentration ratio leads to increased thermal reradiation of the receiver. High reradiation results in low solar absorption efficiencies. This relation is displayed in Figure 2.

Figure 2. Maximum absorption efficiency of a black body at different temperatures and concentration ratios.

Figure 2. Maximum absorption efficiency of a black body at different temperatures and concentration ratios.

In the current analysis, whenever we take the solar absorption efficiency into account, we assume the receiver temperature to be the reduction temperature, because at this temperature the endothermic reaction takes place. Further, we set the concentration ratio to a constant value of C = 4000. This is a quite high value, but for high temperature processes it should be aimed at such high values to avoid drastic thermal losses. Using solar towers together with secondary optics, such high concentration ratios can be reached [14]. Considering the absorption efficiency η_abs, the overall solar to useful work efficiency η_tot is defined as:

$${\eta }_{\text{tot}}={\eta }_{\text{abs}}\times {\eta }_{\text{sc}}$$

(5)

During the following study, the reader should keep in mind that this efficiency formulation represents an ideal thermodynamic description far from real applications. With a concentration ratio of C = 4000, the required temperatures for the direct splitting cannot be reached. The concentration ratios required to reach complete direct gas splitting are close to 8000 (CO₂ splitting) and 20,000 (H₂O splitting). Such high concentration ratios are technically not feasible.

2.3. Two Step Splitting at Normal Pressure, Gas Phase Only

Direct splitting has been discussed before and considered technically not feasible, even when aiming at lower conversion which would relax the temperature exigencies but at the same time require high temperature gas separation [5]. Therefore, thermochemical cycles which increase the entropy difference and thus widen the enclosed area in the T-S diagram have been introduced. Out of many possible cycles with different numbers of intermediate steps, two-step cycling based on redox reactions has drawn most attention of the solar fuels research community [15,16]. In our previous paper we explain the two-step water-splitting process in detail [10]. Here, we directly compare it to the CO₂ splitting process. At first, we introduce only the gas phase entropy change, as this is most generic and the basis of all processes independent of the redox material choice. 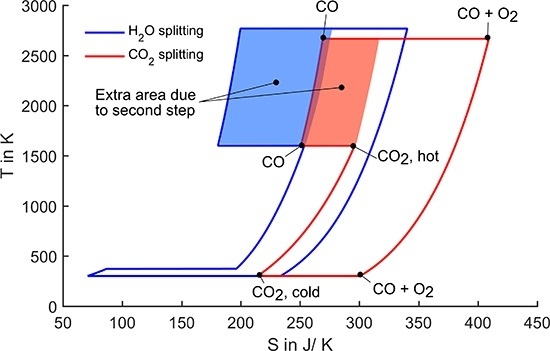The T-S diagram in Figure 3 shows the water-splitting and the CO₂-splitting process. The oxidation temperature is set to 1600 K for both processes. In the following, the CO₂-splitting cycle is explained in detail.

Figure 3. T-S diagram for splitting of one mole of water/CO₂. Oxidation temperature is set to 1600 K, all pressures are 1 bar.

Figure 3. T-S diagram for splitting of one mole of water/CO₂. Oxidation temperature is set to 1600 K, all pressures are 1 bar.

The cycle starts with heating CO₂ from ambient to the oxidation temperature. Then each CO₂ molecule loses one oxygen atom to the redox material resulting in the product gas carbon monoxide. In this step, the entropy decreases, because diatomic CO has lower degree of freedom than triatomic CO₂. In the next step, the redox material is heated to the reduction temperature. At this temperature, oxygen evolves from the redox material leading to a strong entropy increase. This is the endothermal reduction step which requires solar energy input. As the oxygen and the CO evolve at different parts of the process, they are kept separately so that entropy of mixing is not regarded here. In the following step, oxygen and CO are cooled to ambient temperature. Then they are finally recombined to CO₂. In this recombination step, useful work equivalent to the enclosed area in the diagram (Gibbs free energy of formation) can be extracted. There are three options to draw the T-S diagrams above the oxidation temperature:

• In real processes, the product gases (CO and H₂ respectively for CO₂/water splitting) are not heated above oxidation temperature. Therefore, one could exclude their contribution to the overall entropy in the graphs. Then, the entropy would actually drop to zero at the reduction temperature and rise to the entropy of oxygen at the reduction temperature. When cooling the oxygen down from the reduction temperature, the product gas entropy would need to be added leading to a distorted graph, which would be difficult to capture for the reader. Therefore, we did not choose this option.
• The entropy contribution of the product gases could also be considered to stay constant while the reduction takes place. In the T-S representation, this option would result in a straight line upwards after the oxidation reaction and in a slight change of slope at T_ox in the curve representing the cooling of all gases. This kind of representation is easy to grasp visually, but may be confusing, because entropy terms from gases at different temperatures would be added and represented by only one line at T_red. Therefore, we also did not consider this way of representation.
• In the T-S diagrams shown in this paper, the product gas is always heated to the reduction temperature to avoid the confusion which may come up with option 1 or 2. In real applications this heating would not take place. As long as ideal heat recovery is assumed, which is the case in this study, the heating of CO to the reduction temperature does not influence the cycle efficiency. Thus, this is just a question of display and has no effect on the outcome of the analysis.

In the processes shown in Figure 3, all pressures are set to 1 bar. Thus, the only degree of freedom to adjust the area enclosed by the curves is the reduction temperature (the oxidation temperature was set to a fixed value of 1600 K). Although the reduction temperatures still reach very high values of above 2500 K, they could be radically reduced compared to the one-step process. Further, the CO₂-splitting cycle still has a slightly lower reduction temperature than the water-splitting cycle.

The extent to which the reduction temperature can be lowered due to the two-step approach is determined by the shaded areas in Figure 3 labelled extra area due to second step. These areas represent the difference between the one-step and the two-step splitting. It can be directly observed that the impact of the second step is larger in the case of water splitting. In the following paragraph, we give a possible explanation for this difference. However, for a thorough understanding, an ab initio analysis is required, which is not within the scope of this work.

Oxidizing the product gases CO and H₂ to CO₂ and H₂O respectively leads to an entropy decrease, mainly because the number of moles in the gas is reduced. However, the extent of this entropy change differs remarkably between the two splitting processes. In the case of CO₂ splitting, the entropy change is more than 80% larger than in the case of water splitting. This only applies for the temperature range at which water is gaseous (being the relevant temperature range in this context). A possible explanation for this discrepancy is that the CO₂ molecule is linear, while the H₂O molecule is nonlinear. Therefore, CO₂ has two rotational and four vibrational degrees of freedom, while H₂O has three rotational and three vibrational degrees of freedom. As the energy spacing between the rotational energy states is closer compared to vibrational energy states, molecules with more rotational freedom have more possibilities to distribute energy resulting in larger entropy [17]. Nevertheless, CO₂ has higher absolute entropy than H₂O, because it is a larger, heavier molecule. But relative to its weight, water has high entropy which leads to the low entropy decrease when recombining H₂ with O₂. As a straightforward consequence to the above, the reduction of water to hydrogen leads to a large entropy decrease compared to reducing CO₂ to CO.

Resulting from this difference in entropy change, a large temperature gap between oxidation and reduction leads to an advantage of the water-splitting process in terms of potential to lower the reduction temperature. An example of such a case is displayed in Figure 4. Here, the oxidation temperature is set to 800 K and all other conditions are the same as in Figure 3.

Figure 4. T-S diagram for splitting of one mole of water/CO₂. Oxidation temperature is set to 800 K, all pressures are 1 bar.

Figure 4. T-S diagram for splitting of one mole of water/CO₂. Oxidation temperature is set to 800 K, all pressures are 1 bar.

Figure 5. Reduction temperatures corresponding to oxidation temperature with all gases at 1 bar. At oxidation temperatures below 1100 K, water splitting can be performed at lower reduction temperatures than CO₂ splitting.

Figure 5. Reduction temperatures corresponding to oxidation temperature with all gases at 1 bar. At oxidation temperatures below 1100 K, water splitting can be performed at lower reduction temperatures than CO₂ splitting.

Concluding from the above, it is instructive to show the resulting reduction temperature when changing the oxidation temperature. This dependency is displayed in Figure 5. At an oxidation temperature of about 1100 K, the two processes have the same reduction temperature. At higher oxidation temperatures, CO₂ splitting leads to lower reduction temperatures, while water splitting is advantageous at lower oxidation temperatures.

The impact of this trend on the efficiency is displayed in Figure 6. It shows the ideal process efficiency η_sc as well as the total efficiency η_tot which includes solar absorption losses. Regarding the process efficiency η_sc, the CO₂-splitting process is advantageous in the complete range subject to this analysis. This is can be explained by the fact that the extra area due to the second step (as shown in Figure 3) is smaller in the case of CO₂ splitting. This area itself has a poor efficiency, because heat at a high temperature level is dumped. Thus, the process with the smaller extra area has the higher efficiency η_sc. This trend is reversed when taking the solar absorption efficiency into account. A large extra area which considerably reduces the upper process temperature is rewarded by good absorption efficiencies. Thus, at low oxidation temperatures which typically lead to large extra areas, the overall efficiency η_tot of water splitting is higher compared to CO₂ splitting.

Figure 6. Comparison of efficiencies of water splitting and CO₂ splitting. Total efficiency is strongly dependent on reduction temperature.

Figure 6. Comparison of efficiencies of water splitting and CO₂ splitting. Total efficiency is strongly dependent on reduction temperature.

2.4. Two Step Splitting at Reduced Pressure, Gas Phase Only

Up to now, the pressure of all gases was kept at 1 bar in order to introduce the concepts and show general dependencies. However, real applications work with reduced oxygen pressure in the reduction step. This is accomplished by either sweeping with inert gas reducing the oxygen partial pressure or by reducing the total pressure with vacuum pumps. Thermodynamically, these two options are equivalent, so they will not be treated separately in the following.

Typically, the oxygen pressure during reduction is reduced to about 10⁻⁴–10⁻⁵ bar in order to further lower the reduction temperature. The T-S diagram representations of the two cycles with low oxygen pressure during reduction are shown in Figure 7. In the figure, the entropy of the products with oxygen pressure of 1 bar and 10⁻⁴ bar is labelled to show the benefit of lowering the pressure: the oxygen entropy is increased and thus the enclosed area of the cycle increases, too. This results in the possibility to considerably decrease the reduction temperature. In the case of Figure 7, the reduction can take place below 2000 K, while at ambient pressure the reduction temperature would need to be well above 2400 K.

The effect of this temperature reduction on the efficiency is shown in Figure 8, exemplarily for T_oxidation = 1000 K. The process efficiency η_sc is hardly affected by reducing the pressure, because the dominating effect limiting the efficiency is the heat dump at oxidation temperature. Only a slight decrease can be observed when lowering the pressure, because the heat input takes place at lower temperatures. In strong contrast to that, reducing the pressure brings quite a large benefit when taking into account the solar absorption efficiency. From 1 bar to 10⁻⁵ bar, the total efficiency can almost be doubled, because the reduction temperature is decreased by about 600 K.

Figure 7. T-S diagram of splitting one mole of H₂O/CO₂ with reduced pressure. Oxidation temperature is set to 1000 K. Entropy lines of oxygen release at 1 bar and 10⁻⁴ bar are shown to visualize the effect of reduced pressure.

Figure 7. T-S diagram of splitting one mole of H₂O/CO₂ with reduced pressure. Oxidation temperature is set to 1000 K. Entropy lines of oxygen release at 1 bar and 10⁻⁴ bar are shown to visualize the effect of reduced pressure.

Figure 8. Influence of reducing the pressure on the reduction temperature and the efficiency; T_ox = 1000 K.

Figure 8. Influence of reducing the pressure on the reduction temperature and the efficiency; T_ox = 1000 K.

However, when interpreting this increase of the total efficiency, one should consider that applying a vacuum as well as flushing with inert gas bring along large irreversibilities reducing the efficiency [8,18,19]. Therefore, the pressure reduction should mainly be considered as a technical advantage rather than an efficiency boost.

2.5. Two Step Splitting at Reduced Pressure, Gas and Solid Phase

A possible approach in system design is to define the temperature limits which are technically reasonable and then use a material which can work at these temperatures. A typical material candidate for such an approach is ceria. It can be reduced from CeO₂ to CeO_2-δ with values of δ reaching from 0 to 0.5. In the relevant temperature range, ceria does not undergo a phase change, but δ increases steadily with increasing temperature and decreasing oxygen pressure. The entropy change in the material per mole of oxygen released is considerably higher at low values of δ [20]. The explanation for this effect is the higher configurational disorder caused by the first oxygen atoms leaving the crystal structure. The drawback of low values of δ is a high thermal mass which needs to be cycled between oxidation and reduction temperature at low fuel generation rates. Thus, the lower the δ, the more important becomes solid phase heat recovery [7,21].

For a complete analysis of a specific redox material, it is important to also consider the enthalpy of reaction. Only then, it can be determined if a certain process can be accomplished at selected temperature levels. But in this analysis we want to point out the entropy requirement and discuss it in a vivid way together with the efficiency. The enthalpy of reaction is assumed to be always of the value which is necessary to make the reaction feasible. This idealization should be kept in mind when dealing with specific materials. Thus, in this paper we show the highest possible efficiency which could be reached with materials perfectly matching the process conditions.

Figure 9 shows the T-S diagram with typical process parameters in the range of recent projects realizing solar thermochemical cycles [22]. The reduction takes place at 1700 K and a pressure of 10⁻⁵ bar. The oxidation temperature is set to 1300 K. In order to keep the representation of the T-S diagrams consistent and generic, we do not include the absolute entropy value of a possible redox material. Instead, we only include the entropy difference during oxidation and reduction. The dashed lines in Figure 9 represent the gas phase entropy only. The required extra entropy change which needs to be undergone by the redox material in order to reach the necessary ΔG is also marked in the figure.

Figure 9. T-S diagram of splitting one mole of H₂O/CO₂ at defined reaction temperatures. The entropy change required by the redox material is marked.

Figure 9. T-S diagram of splitting one mole of H₂O/CO₂ at defined reaction temperatures. The entropy change required by the redox material is marked.

Analogous to the example in Figure 9, we determined the required entropy change in the redox material for different process conditions, see Figure 10. The oxidation temperature is varied on the x-axis, the reduction temperature is varied by setting the temperature difference between oxidation and reduction to dT = 200 K and dT = 400 K. The results are shown for a reduction pressure of 0.1 bar and 10⁻⁵ bar. The graphs show that at oxidation temperatures above 1100 K, the entropy exigencies regarding the redox material are less demanding in the case of CO₂.

Figure 10. Required entropy change in the redox material per mole of H₂O/CO₂.

Figure 10. Required entropy change in the redox material per mole of H₂O/CO₂.

However, at oxidation temperatures below 1100 K, the opposite is the case: water-splitting does not require such a high entropy change in the redox material. This trend can again be explained by the extra area which the second step generates in the T-S diagram (see Figure 3). If that area plays a dominant role—which is the case at low process temperatures—the water-splitting process is advantageous, because the entropy change in the gas phase during oxidation is larger. Further, lower reduction pressures also lead to a decrease of the required redox material entropy change.

The total efficiency of the process is shown in Figure 11 for the same parameter set used in Figure 10. The effect of the oxidation temperature on the efficiency has been discussed before [10]. It can be summarized as follows: at low oxidation temperatures the heat loss accompanied with the oxidation step is dominating the efficiency. If that heat loss takes place at higher temperatures, the efficiency drops. However, at one point the influence of that heat loss is overruled by the positive effect of rising heat input temperatures. Then, the efficiency rises again with rising temperatures.

Figure 11. Total theoretical efficiency of solar water splitting at different process conditions.

Figure 11. Total theoretical efficiency of solar water splitting at different process conditions.

Further, lower reduction pressures are beneficial for the absorption efficiency, as discussed above when considering the gas phase only. Reducing the temperature difference to dT = 200 K, the efficiency drops remarkably. This is again due to the large influence of the heat loss during oxidation.

Figure 12 shows an example of such a process with low dT. The strong influence of the large area associated to the second step is clearly visible. In this case, the heat released during oxidation should be coupled to a secondary process. Energetically, the thermochemical cycle could surely always be extended with secondary processes using all waste heat and thus leading to the Carnot efficiency between the reduction temperature and ambient temperature. Technically and economically however, such an approach is not always feasible.

Figure 12. T-S diagram of splitting one mole of H₂O/CO₂ at an oxidation temperature of 1300 K and a reduction temperature of 1500 K.

Figure 12. T-S diagram of splitting one mole of H₂O/CO₂ at an oxidation temperature of 1300 K and a reduction temperature of 1500 K.

3. Conclusions

We have conducted a comprehensive study on the efficiency of solar thermochemical splitting cycles. The study is based on an approach using mainly T-S diagrams, hence emphasizing graphical explanations rather than the underlying equations. A previous study analyzing the purely thermochemical process efficiency of water splitting was extended. On the one hand, CO₂-splitting cycles were analyzed and compared to the previous results. On the other hand, the solar absorption efficiency was included in the overall efficiency calculation.

CO₂ splitting is in many cases advantageous compared to water splitting regarding the efficiency. This is due to the higher entropy change which occurs when recombining CO with oxygen compared to H₂. However, when splitting CO₂, the low entropy change in the gas phase during the oxidation step can lead to higher demands regarding the redox material. The entropy difference in the solid between the oxidized and the reduced state needs to be higher in some cases, especially when operating at low temperatures.

The study has theoretical thermodynamic character only and should therefore only help understanding the general principles of the analyzed cycles. Real applications have to cope with many other factors like heat recovery from solids, efficiency cutbacks due to means to create an oxygen deficient atmosphere and many more. This should be kept in mind when interpreting the efficiency values. Furthermore, the redox material entropy values shown here are only valid in combination with certain enthalpies of reaction. Therefore, no specific material analysis was conducted here. Also especially at low temperatures, slow kinetics may impede the process to practical infeasibility. Thus, this study does not intend to present real process efficiencies, but rather to provide the relevant thermodynamic background every process developer should have when trying to bring theory into practice.