iDoRNA: An Interacting Domain-based Tool for Designing RNA-RNA Interaction Systems

Abstract

RNA-RNA interactions play a crucial role in gene regulation in living organisms. They have gained increasing interest in the field of synthetic biology because of their potential applications in medicine and biotechnology. However, few novel regulators based on RNA-RNA interactions with desired structures and functions have been developed due to the challenges of developing design tools. Recently, we proposed a novel tool, called iDoDe, for designing RNA-RNA interacting sequences by first decomposing RNA structures into interacting domains and then designing each domain using a stochastic algorithm. However, iDoDe did not provide an optimal solution because it still lacks a mechanism to optimize the design. In this work, we have further developed the tool by incorporating a genetic algorithm (GA) to find an RNA solution with maximized structural similarity and minimized hybridized RNA energy, and renamed the tool iDoRNA. A set of suitable parameters for the genetic algorithm were determined and found to be a weighting factor of 0.7, a crossover rate of 0.9, a mutation rate of 0.1, and the number of individuals per population set to 8. We demonstrated the performance of iDoRNA in comparison with iDoDe by using six RNA-RNA interaction models. It was found that iDoRNA could efficiently generate all models of interacting RNAs with far more accuracy and required far less computational time than iDoDe. Moreover, we compared the design performance of our tool against existing design tools using forty-four RNA-RNA interaction models. The results showed that the performance of iDoRNA is better than RiboMaker when considering the ensemble defect, the fitness score and computation time usage. However, it appears that iDoRNA is outperformed by NUPACK and RNAiFold 2.0 when considering the ensemble defect. Nevertheless, iDoRNA can still be an useful alternative tool for designing novel RNA-RNA interactions in synthetic biology research. The source code of iDoRNA can be downloaded from the site http://synbio.sbi.kmutt.ac.th.

1. Introduction

Currently, RNA-RNA interactions have gained much interest as they play a crucial role in gene regulation for both prokaryotes and eukaryotes [1,2,3,4]. Systems that are based on RNA-RNA interactions have been utilized in various applications, including medicine, agriculture and industry. For instance, gene inhibition systems based on the interaction of small interfering RNAs (siRNAs) with their target genes have been widely used for suppression of cancer-related genes as a means for cancer therapy [5,6]. A system employing antisense RNA developed for controlling petunia flower color is a good example of an RNA-RNA interaction application in agriculture [7]. In addition, a regulatory system based on small RNAs (sRNAs) has been developed in an Escherichia coli (E. coli) system for controlling, tuning and monitoring specific genes involving response to toxins, DNA damage and cell death [8]. This programmed bacterium has great potential for industrial applications. With its great potentials, RNA-RNA interactions have already become a topic of interest among synthetic biologists who are exploring and developing new artificial RNA-RNA interaction-based systems with broader applications.

For successful development of RNA-RNA interaction-based regulation systems, computational tools that can help in the design of targeted RNA sequences and structures are needed. Computational design tools can help in minimizing adverse regulation resulting from undesired RNA interactions. Moreover, they can reduce the time spent in laborious experimental studies. So far, the various computational tools that have been developed for designing RNA molecules can be divided into two groups: first, tools that specifically aim to design structure-based RNAs; e.g., RNAInverse [9], RNA-SSD [10], INFO-RNA [11], MODENA [12], NUPACK [13], and RNAiFold [14]. Since the functions of the required RNAs are directly related to their structures, the purpose of these design tools is to provide the best RNA sequences that can fold into the target secondary structures given by a user. These structure-based RNAs have been used as gene regulators in response to external signals such as a riboswitch [15,16] and a thermometer-RNA [17] having metabolites and temperature as the external signals, respectively. The other group of computational design tools is principally for designing antisense-based RNAs (i.e., siRNAs) used for suppression of target genes. Thus, these tools take into consideration the context sequences of siRNA and its accessibility to target mRNA. Tools of this type include siDirect [18], DEQOR [19], AsiDesigner [20], DSIR [21], and DEsi [22]. Although the abovementioned RNA design tools have been useful, they are limited to designing single RNA molecules which in turn limits their applications.

In the field of synthetic biology, RNA-RNA interaction is used as a foundation for construction of a few biological regulators in synthetic organisms. For example, cis-and trans-encoded RNAs have been employed to create various regulators; e.g., on/off switches [23,24], a comparator [25] and logic gates [26]. These devices serve as diverse molecular controllers necessary for the creation of programmable cells. Despite the increasing interest in RNA-RNA interactions, novel devices and systems based on these molecular interactions are still limited in number. The design of novel RNA-RNA interaction-based systems requires careful consideration of conformational changes in RNA structures resulting from intermolecular and intramolecular interactions. The conformational changes in RNA structures before and after their interaction dictate the functions. Thus, a good RNA-RNA interaction design tool should provide reliable sequences of two RNAs, which can form multi-state structures at both folding states before and after RNA-RNA interaction [24,27]. “Multi-state structures” refers to two RNA changeable molecules that can fold into three distinct structures; i.e., two independent structures of two RNA molecules that further interact to form a third independent hybridized RNA molecule structure. Nevertheless, only a few RNA tools such as NUPACK [13], RNAiFold [14,28], RiboMaker [29] and iDoDe [30] are able to cope with this challenge. NUPACK is a remarkable design tool that provides nucleotide sequences for supporting the inverse folding problem. The tool uses a substructure decomposition strategy for dividing the target structures and finding a proper sequence by minimizing the ensemble defects [13]. Although, this tool is able to design multi-state target structures that support the RNA-RNA interaction design problem, it still requires a user-assigned substructure for initialization. RNAiFold is another outstanding tool that uses constraint programming (CP), and a large neighborhood search (LNS) to design hybridized RNA structures. The design method attempts to find optimal sequences of two RNA molecules whose MFE hybridized structure is identical to a target hybridized structure. However, RNAiFold does not support multi-state structures [14,28]. Recently, RiboMaker has been developed for providing RNA sequences of two molecules corresponding to multi-state target structures [26,29]. This tool applies the evolutionary algorithm of Monte Carlo Simulated Annealing (MCSA) to optimize a thermodynamic function in order to design conformation-based riboregulation; i.e., bacterial small RNAs (sRNAs) in the 5′-untranslated region of its target mRNA. At the same time, we proposed another design tool, namely interacting domain-based design (iDoDe), that provides RNA sequences with a set of intermolecular and intramolecular folded structures [30]. The iDoDe program applies a domain-based decomposition and a stochastic algorithm proposed by Zhang [31] to generate suitable RNA-RNA interactions. We showed that iDoDe was able to reduce the search space and unwanted interactions, and provided RNA sequences which can fold into a given structure for simple RNA-RNA interactions without any unwanted interactions. However, iDoDe falls short in satisfying the design of complex RNA-RNA interactions, mainly due to its stochastic approach. To overcome this limitation, an optimization algorithm had to be incorporated into the iDoDe algorithm to help efficiently design these RNA-RNA interactions.

Several optimization methods have been applied to the field of molecular biology including expectation maximization [32,33,34], simulated annealing [35,36,37], machine learning [38,39], linear programming [40,41,42], and the genetic algorithm (GA) [43,44,45,46,47]. Among them, the GA is a well-known heuristic and evolutionary algorithm used in many RNA-based tools to solve diverse RNA problems. Computationally, the GA evolves solutions of a population through a recurrent searching process of genetic operations including selection, crossover, and mutation. Each RNA solution or individual is assigned a fitness value indicating its goodness, which serves as an objective function. For example, in the RNA alignment tools, the GA seeks and clusters similar mRNAs in a genome through repeatedly determining their similarity and distance [46,48]. On the other hand, some RNA structure prediction tools use the GA to find a near optimal secondary structure by minimizing the free energy of RNA structures [47,49]. In the case of RNA design tools, the GA was also used to find near optimal RNA sequences corresponding to user’s requirement [12,50]. Consequently, with the help of the GA, it is possible to gain a near optimal solution of a given RNA-RNA interaction.

Using a genetic algorithm, we have developed an improved tool called iDoRNA that helps to design interacting domain-based RNA-RNA interactions. The iDoRNA program can provide a near optimal RNA-RNA interaction set corresponding to the given requirements. In this article, we show that iDoRNA can efficiently design various sets of RNA-RNA interaction systems; e.g., S1-A1, and crRNA-taRNA. In comparison with iDoDe, iDoRNA performs much better in terms of both accuracy and computational time usage. When compared with the benchmark tools; i.e., NUPACK, RNAiFold 2.0 and RiboMaker, iDoRNA performs better than RiboMaker, but is outperformed by NUPACK and RNAiFold 2.0.

2. Methodology

2.1. Description of the Algorithm of iDoRNA

The iDoRNA algorithm developed in this work combines our previous algorithm used in iDoDe [30] and a genetic algorithm (GA) [51] to help design a near optimal RNA individual for a given RNA-RNA interaction. The workflows of iDoDe and iDoRNA are shown in Figure 1a,b. In this section, we describe the details of the iDoRNA algorithm.

2.1.1. Representation of an RNA Individual

The representation of an RNA individual is illustrated in Figure 2. An RNA individual is a set of two single-stranded RNAs (R1, R2) that can fold into themselves and bind to each other to form a hybridized RNA (HR) possessing a specific structure and function. R1, R2 and HR are strings of nucleotide sequences; i.e., R1.seq, R2.seq, and HR.seq, respectively. There are five properties used to characterize an RNA individual including (i) minimum free energy RNA structure, (ii) Hamming distance, (iii) similarity score, (iv) stability score and (v) fitness score. In iDoRNA, a population size (n) of the individuals is specified for GA optimization, and thus the number of total RNA individual is n per each population.

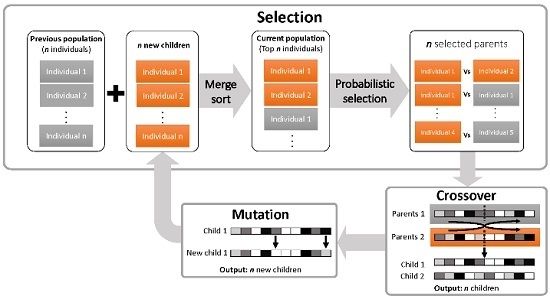
2.1.2. The iDoRNA Algorithm

iDoRNA consists of three main modules including initialization, evaluation and reproduction as shown in Figure 1b. The description of each module is detailed as follows.

Initialization

To design an RNA-RNA interaction system with iDoRNA, a user must provide the desired lengths and secondary structures of R1, R2 and HR that make up the system. The user then provides additional constraints regarding nucleotide sequences on specific regions such as start codons and ribosome binding sites (RBS) by assigning uppercase letters of IUPAC codes to the constrained regions while leaving non-specified bases with the letter “N”. To represent the secondary structure of each RNA, a dot-bracket notation is used, where “.” refers to an unpaired base, “(“ and “)” refer to paired bases and “&” is a separator between R1 and R2 within the structure representation of the HR.

With the given user’s input information, iDoRNA begins to design the sequences of R1, R2 and HR by first generating an initial population of n individuals using the initialization method of iDoDe as briefly described below. The details of the initialization method are also described in the Supplementary Information.

Step 1: The target structures of R1, R2, and HR provided by the user are first divided into a set of domains (D), defined as a substructure representing either interacting or non-interacting segments. A set of domains consists of D₁, D₂, …, D_m, where the subscript m is the number of domains. The details and the examples of the interacting domain-based decomposition are described in the Supplementary Method and the Supplementary Figure S1, respectively. Each domain D is a string of ℓ bases: r₁, r₂, …, r_ℓ, where r ϵ {a, c, g, u, A, C, G, U} and the subscript ℓ is the domain length.

Step 2: In this step, all non-specified bases originally assigned by the user as “N” in all domains are randomly replaced with lowercase RNA bases (a, c, g, or u) by using the Domain-based Design (DD) algorithm [31].

Step 3: All domains (D₁ to D_m) are concatenated into the 3 RNA strands; R1, R2, and HR, indicated by R1.seq, R2.seq, and HR.seq, respectively. Each concatenated single-stranded RNA (R1.seq or R2.seq) is a string of L bases: r₁, r₂, …, r_L in the 5’-3’ direction, where the subscript L is the RNA length. On the other hand, the concatenated hybridized RNA strand (HR.seq) is a combined string of R1.seq and R2.seq separated by the symbol “&”. This set of R1, R2 and HR is referred to the first RNA individual.

Step 4: Steps 2 and 3 are repeated n times to generate concatenated RNA strands of n individuals.

Evaluation

Each RNA individual is evaluated for its five properties mentioned in Section 2.1.1. The definition and the calculation of each property are given below:

Minimum Free Energy RNA Structure

A minimum free energy RNA structure is a secondary structure with the minimal free energy (MFE) of a designed RNA sequence represented by a dot-bracket notation. Given R1.seq, R2.seq, and HR.seq as input, the MFE secondary structures of R1, R2, and HR are predicted using the Vienna RNA package [52]. Within this package, RNAfold is used to predict the structures of R1 and R2 (R1.str and R2.str), and RNAduplex is used to predict the structure of HR (HR.str). Additionally, the value of minimal free energy of the HR structure (MFE_hr) is further used to calculate the stability of a designed RNA individual.

Hamming Distance

In iDoRNA, the Hamming distance is applied to measure the difference in the structures of a designed individual with the target structures specified by the user. It is determined by the summation of distinct positions of the given individuals relative to the target. A position with a distinct structure is assigned a value 1; otherwise it is assigned a value 0. For instance, the Hamming distance of the hybridized RNA shown below has a value of 4 because there are four distinct positions between the required and designed structures as indicated by the red positions.

Target HR structure:	.....((((((.....))))))$\mathbf{\left(}\mathbf{\right(}$(((((((((((&............)))))))))))$\mathbf{\left)}\mathbf{\right)}$
HR.str:	.....((((((.....))))))$\mathbf{.}\mathbf{.}$(((((((((((&............)))))))))))$\mathbf{.}\mathbf{.}$
HR.hd = 4	0000000000000000000000$\mathbf{1}\mathbf{1}$00000000000-00000000000000000000000$\mathbf{1}\mathbf{1}$

For each RNA individual, there are three values of the Hamming distances: R1.hd, R2.hd, and HR.hd.

Similarity Score

The similarity score (f_sim) is the value that indicates how similar the structures of a designed RNA individual is to the target structures. The f_sim is calculated by Equation (1):

$$f_{sim}=\frac{1}{3}{\displaystyle \sum _{i=1}^3\left\{\frac{L_i-H{D}_i}{L_i}\right\}}$$

(1)

where HD_i is the hamming distance of the i-th RNA and L_i indicates the length of the i-th RNA. Note that f_sim has a value ranging from 0 to 1; where 0 indicates a poorly designed structure while 1 indicates a well designed structure of an RNA individual.

Stability Score

The stability score (f_sta) is the relative stability of an RNA individual. In this study, f_sta was calculated based on the ratio of hybridization energy of an MFE structure of a designed HR to the reference energy. Previous studies have shown that the hybridization energy of hybridized RNAs has a highly negative correlation with biological activity [24]. Thus, in this study, the hybridization energy of hybridized RNA structure was used to represent the stability property of designed RNAs in our tool. In general, a lower hybridization energy would lead to a more stable hybridized RNA, which is more biologically active. Nevertheless, too low a hybridization energy could lead to a hybridized RNA with too high a rigidity in the resulting structure and a consequent lack of the necessary conformational dynamic properties, which in turn lead to a poor biological activity [53]. To avoid the hybridization energy from being too low during energy minimization, we set the reference hybridization energy (MFE_ref) as the target energy. Since the structural rigidity of a RNA duplex depends on its %GC content, we set the target energy as a function of %GC content and length of the RNA duplex, which can be defined by users. Throughout of this work, we set the %GC content at 50, which is an average content in Escherichia coli genome [54]. Thus, the calculation of the stability score (f_sta) is performed using the following mathematical expressions:

$$f_{sta}=\frac{MF{E}_{HR}}{MF{E}_{ref}}; \text{if} f_{sta}>1, f_{sta}=1$$

(2)

$$MF{E}_{ref}=(MF{E}_{GC,100\%}\times (\frac{\%GCcontent}{100}))+(MF{E}_{GC,0\%}\times (1-\frac{\%GCcontent}{100}))$$

(3)

where MFE_GC,100% and MFE_GC,0% are the hybridization energy of the duplex structure in the required HR at 100% and 0% GC content, respectively. These values represent the highest and the lowest stability of a given length of required HR structure. These 2 energies were obtained from Equations (4) and (5), respectively:

$$MF{E}_{GC,100\%}=-3.30(N_{bp})+7.40$$

(4)

$$MF{E}_{GC,0\%}=-0.89(N_{bp})+5.02$$

(5)

where N_bp is the total number of paired bases (or HR length) of the required HR structure. All constants were obtained from linear regression of relationship between calculated MFE (by RNAcofold [52]) of double-stranded segments and their length (N_bp) for the case of 100% and 0% GC contents. Note that f_sta has the value from 0 to 1; 0 indicates the least stable while 1 indicates the highest stable structure of an RNA individual when compared with 50% GC-containing RNA duplex of the same size. Thus, an RNA individual with f_sta near 1 would have a high hybridization energy and thus high biological activity.

Fitness Score

To realize the objective design, iDoRNA simultaneously optimizes two RNA properties, similarity and stability of designed RNA structures, by maximizing the fitness score (F), represented by f_sim and f_sta. The fitness score is expressed as shown in Equation (6):

$$F=({\omega }_{Sim}\times f_{sim}+(1-{\omega }_{Sim})\times f_{sta})$$

(6)

where ω_Sim is a weighting factor of similarity. By this expression, F ranges from 0 to 1, where 1 indicates a perfectly designed RNA individual. In iDoRNA, F is maximized during the GA optimization.

Reproduction

Reproduction is the module that determines an optimal individual based on GA which follows a step of natural selection; i.e., crossover and mutation. To find an optimal RNA individual, new RNA individuals are repeatedly rebuilt by genetic operations for improvement of designed RNAs. The steps of reproduction based on GA are summarized in Figure 3, and described in details as follows.

Selection Step

The number of individuals (n) obtained from the mutation step (called new children) are first combined with the n individuals of a previous population. The 2n individuals of the combined population are ranked in descending order of the fitness score by the merge sort algorithm [55]. The top n individuals are used as a parent pool. Note that for the first generation, the initial population of n individuals obtained from the initiation step is directly used as the parent pool. Next, the n-parents (or n/2-parent pairs) are selected from the parent pool using a probabilistic function, defined as the fractional fitness of the parent. This probability of a parent is calculated by the ratio of the fitness score of the parent to the sum of the finest scores of all parents. Then, pseudo-random numbers (N_rand) in the range of [0,1] are generated one at a time, and used for choosing n parents for the crossover. If an N_rand value is in a probability space of a parent, such a parent is selected. Thus, the chance of a parent being selected is directly proportional to its fractional fitness. Note that a parent pair must not include the same parent meaning parent 1 cannot pair with parent 1.

Crossover Step

Having selected n-parents, the sequences of R1 and R2 in each parent are improved by the recombination of corresponding RNA domains (D) between each parent pair. To choose which D is to be recombined, we set up a crossover rate (Cr) as a parameter for recombination acceptance ranging from 0 to 1. Repeatedly, N_rand is randomly generated one at every D of an individual and compared to Cr. A given D is accepted for a recombination between a parent pair when N_rand is less than Cr. Thus, a crossover operation frequently occurs if Cr is set high, and vice versa. If a D is accepted for recombination, a position on the D (between r₁ and r_l) is randomly generated to choose a recombination point. An illustration of crossing over of a parent consisting three RNA domains (D1–D3) with different l lengths is shown below. It can be seen that the recombination only occurs on D1 and D3 because the N_rand for each domain is less than a given Cr. After the crossover is finished, two new individuals called child 1 and child 2 are obtained.

Mutation Step

n-Children obtained from the crossover step are subjected to mutation for further improvement of R1 and R2 sequences. In this step, for every single base position of R1 and R2 in each child, a N_rand is generated and used to pick a point of mutation by comparing it with a mutation rate (Mr). Mr is defined as a parameter for mutation acceptance, which is in the range of 0 to 1. If the N_rand value of a base position is less than a given Mr, then such a base is to be mutated by altering it to one of the other possible bases. Once, the mutation step is finished, a new set of n-children is obtained. These children are subsequently ranked in descending order according to fitness scores, and used as a new population for further improvement in the next iteration.

Termination Criteria

In iDoRNA, there are two termination criteria: (i) the highest value of the fitness score of a population is unchanged for 30 consecutive runs and (ii) the generation number reaches a defined maximum number of iterations (N_term). In this work, we set N_term to 1000 generations. Therefore, iDoRNA is terminated when one of the two criteria is met, and then provides a best predicted (or near optimal) RNA individual as output.

2.2. Parameter Optimization

Important parameters involving the genetic algorithm were investigated to see their effects on the design performances of iDoRNA. These parameters include weighting factor of similarity (ω_sim), population size (n), crossover rate (Cr), and mutation rate (Mr). An RNA-RNA interaction system of crR12-taR12 [23] was used as a target design. The optimal value of each parameter is chosen based on the fitness score and computational time.

2.3. Performance Assessment

For performance assessment, forty-four different RNA-RNA interaction models with different levels of structural complexity were used (Supplementary Data S1). These models can be divided into two groups; actual RNAs and artificial RNAs. Actual RNAs (models N01-N07) are the RNA structures and specific sequences of a pair of RNAs that function in natural systems. On the other hand, artificial RNAs (models A01-A37) are the RNA structures that we made up.

Models N01 to N07 were taken from previous experimental studies without pseudo-knot structure [23,24,56,57,58,59,60]. The first two models called AS::S1 and taRNA::crRNA systems are proven to successfully regulate a gene expression in vivo by mimicking the natural RNA structures and motifs of RNA-OUT::RNA-IN and Hok::Sok, respectively [23,24]. Models N03 to N07 are natural RNA-RNA interactiona, which play a prominent role in post-transcriptional regulation [56,57,58,59,60]. DsrA of models N03 and N07 are involved in a translational regulation of mreB and RpoS in response to cold stress [56,60]. While RyhB of models N04 and N06 blocks the translation of sodB and ompA and triggers the degradation of both RNAs [57,59]. In model N05, FinP involves the control of cell conjugation by binding traJ, 5’ untranslated-region of tra gene [58]. Models N01 to N07 possess high complexity in structures at both single-stranded structures, R1 and R2, and their corresponding HRs (see Supplementary Data S1 and S2).

For the artificial models, models A01-A04 are simple models taken from Thaiprasit et al. [30]. They are simple RNA structures consisting of linear segments and hairpin-loops structures (R1 and R2 in Supplementary Data S1 and S2) in the intramolecular folding state and different hybridized structures (HR in Supplementary Data S1 and S2) at the intermolecular folding state, where all R1 molecules of models A01-A04 are linear segments having a primary RNA structure with increasing lengths (10 to 15 nt), whereas R2 molecules represent either a primary structure (i.e., linear segment in model A01) or a secondary structure (i.e., hairpin-loops in models A02-A04) in the size of 10 to 30 bp. At the intermolecular folding state, interactions between R1 and R2 molecules give hybridized structures of double-stranded RNA, except for models A03-A04 that also exhibit hairpin-loop structure in R2.

Unlike models A01-A04, models A05-A37 were built from the set of benchmarking single stranded RNAs given by Garcia et al. [14,28]. These single stranded RNAs are regulatory RNAs that are able to function in Nature. In this study, we created the thirty-three artificial models of RNA-RNA interaction from the set of single stranded RNA molecules as follows. Firstly, sequences and dot-bracket structures of all benchmarking set available on RNAiFold [14] web server were downloaded. Secondly, thirty-three sets whose lengths are less than 250 nucleotides were selected for providing an input of RNA-RNA interaction model. Thirdly, an RNA strand of each set was divided into two strands using the following criteria: (1) if the number of paired bases of such RNA is less than 15 pairs, the RNA strand was split at the position that yields the highest number of pair bases of HR structure, (2) if the number of paired bases of such RNA is more than 15 pairs, the RNA strand was divided equally. Fourthly, dot-bracket structures of all individual RNAs and hybridized RNA were determined by using RNAfold and RNAcofold of Vienna RNA package 2.1.8 [52], and used as artificial test models (Supplementary Data S1).

For the tool assessment, iDoRNA was first compared its performance with iDoDe, and then against three benchmark tools; i.e., NUPACK [13], RNAiFold 2.0 [28] and RiboMaker [29]. Models N01-N02 and A01-A04 were used for the first comparison with 30 independent trials, while all forty-four test models were used to perform the latter with 10 independent trials. The best individuals were analyzed using ensemble defect, fitness scores and computational time usage as criteria. When comparing with iDoRNA, iDoDe randomly designs each RNA model using the same computational time required in iDoRNA. The RNA individuals with the highest fitness score was compared with the optimal score of the RNA individual suggested by iDoRNA. In addition, the success rate, which is defined as the ratio of RNA individuals with perfect design (F = 1) to the total number of the designed RNA individuals of both methods were compared to assess the performance. For the comparison of iDoRNA with the benchmarks, the following procedure was used.

For NUPACK and RNAiFold 2.0, the tools were performed on design option that allows only one target structure of either individual RNA or hybridized RNA. In this study, targets of design for NUPACK and RNAiFold 2.0 were prepared from sequences and secondary structure of hybridized RNA. For design RNA-RNA interaction using RiboMaker, the same input target structures and constrained sequences used for iDoRNA were used as input. The default parameters; iteration numbers of 5000 and Monte Carlo temperature of 1 were used. In this work, all of the designs were performed on a machine with an Intel^® Core™ i7-4790 Processor 1600 MHz and 16 GB RAM.

3. Results and Discussion

In this study, we have incorporated a genetic algorithm (GA) into our previous RNA tool (iDoDe) to help optimally design a given RNA-RNA interaction system. This tool is renamed to iDoRNA, which stands for interacting domain-based design tool of RNA-RNA interaction. Herein, we present the effects of the parameters on design performance and, later, compare the performance of iDoRNA with that of iDoDe and benchmark iDoRNA against three other available design tools: i.e., NUPACK, RNAiFold 2.0 and RiboMaker.

3.1. Suitable Parameters for iDoRNA

To optimize the performance of iDoRNA, we studied the sensitivity of some parameters to the tools’ performances in designing an RNA-RNA interaction system. These parameters include weighting factor (ω_sim), crossover (Cr) and mutation (Mr) rates, and population size (n). To maintain the computational time and the existing complex structure, the RNA-RNA interaction system used for this test is the crRNA-taRNA system (model N02), which contains basic structural elements: unpaired nucleotide, paired base, hairpin loop, bulge, and internal loop.

3.1.1. Effect of the Weighting Factor of Similarity

To study the sensitivity of the weighting factor of similarity on the iDoRNA performance, we set the values of ω_sim at 0.3, 0.5, 0.7, and 1.0 while keeping the values of Cr, Mr, and n constant at 0.9, 0.1 and 10, respectively. The performance was determined by observing the similarity and stability scores of the RNA individuals at various generations (Figure 4). At the generation zero, the properties of the initial RNA individuals generated directly from the iDoDe algorithm are fairly diverse, with the similarity score ranging from 0.65 to 0.96, and the stability scores ranging from 0.7 to 1 (Figure 4a). It is noteworthy that the best individual at this initial population was found to possess the similarity and stability scores of 0.906 and 0.965, respectively. After these sets of individuals have gone through several rounds of natural selection with the genetic algorithm, the properties of all individuals have been improved with the number of generations (Figure 4b–d). These improvements can be observed by the movement of the RNA individuals’ properties towards the upper right-hand corner of the plots where both the similarity and stability scores are high, except for the case where the weighting factor equals to 1. It can also be seen that the properties of the RNA individuals designed with ω_sim at 0.3, 0.5, and 0.7 are similar. However, the ω_sim of 0.7 was chosen as the suitable parameter for further study because it provides a relatively faster convergence and better overall properties.

3.1.2. Effect of the Crossover and the Mutation Rates

To study the sensitivity of the crossover and the mutation rate parameters on the iDoRNA performance, we first varied the values of Cr from 0.1 to 0.9 while keeping Mr constant at 0.1 and the population size of 10. The plots of the fitness score versus the generation indicated that Cr of greater than 0.5 appeared to give fast convergence (Figure 5a). The Cr of 0.9 was chosen for further study, as it requires the least number of generations to reach the optimum. Conversely, when we increased the values of Mr from 0.1 to 0.9 while keeping the Cr constant at 0.9, the required number of generations to achieve the optimum was increased (Figure 5b). Thus, the most suitable value of the mutation rate was 0.1. Notably, the sensitivity of the design performance to the mutation rate is more than that to the crossover rate, indicating that a slight change of the mutation rate would affect the tool’s performance greatly, so this parameter should be considered carefully when performing a design of a more complex RNA-RNA interaction system.

3.1.3. Effect of the Population Size

To see how the population size affects the performance of iDoRNA, we varied the population sizes from 4 to 100 RNA individuals per population. For each population size, ten independent runs were performed, and the optimal RNA solutions and the averaged computational time were compared (

Table 1. Effect of different population sizes (n) on computational time and fitness score.

Population Size	Computational Time (s) *	Optimal Fitness *
4	11.50 ± 1.90	0.993 ± 0.006
6	16.10 ± 2.42	0.995 ± 0.003
8	22.30 ± 3.77	0.996 ± 0.000
10	26.00 ± 5.19	0.996 ± 0.000
20	48.30 ± 6.68	0.996 ± 0.000
50	106.80 ± 7.87	0.996 ± 0.000
100	202.00 ± 14.52	0.996 ± 0.000

* The values shown are the average and its standard deviation from 10 independent runs.

). It can be seen that both the optimum fitness and the required computational time increase as n is increased. However, the optimum fitness reached its maximum at 0.996 when n was equal to or greater than 8. Thus, the population size of eight RNA individuals was preferable since it required the least computational time while still providing the maximum fitness. In summary, optimum values of the weighting factor, the crossover rate, the mutation rate and the population size were 0.7, 0.9, 0.1, and 8, respectively. These values was then used in the subsequent assessment of the iDoRNA tool.

3.2. Design Performance of iDoRNA

To elucidate the design ability of iDoRNA, we employed the program to design six artificial RNA-RNA interaction models with increasing structural complexity. Thirty independent runs were performed for each model using the suitable set of GA parameters obtained from the previous step.

Table 2. Representation of the design performances of iDoRNA on computational time and fitness score corresponding to number of IDs.

Model No.	RNA Complexity		Computational Time (s) *	Optimal Fitness *
	Length of R1/R2 (Nucleotides)	Number of ID
A01	10/10	3	4.8 ± 0.53	1.000 ± 0.000
A02	15/15	3	4.5 ± 0.50	1.000 ± 0.000
A03	10/20	4	6.3 ± 0.87	1.000 ± 0.000
A04	15/30	5	6.4 ± 0.56	1.000 ± 0.000
N01	35/67	17	17.1 ± 4.61	0.994 ± 0.001
N02	55/71	24	21.3 ± 3.76	0.996 ± 0.002

* The values shown are the average and its standard deviation from 30 independent runs.

shows that iDoRNA was able to perfectly design models A01-04 as seen by the fitness score of 1.

However, for models N01 and N02 that are more complex in structure, our tool was able to design them with the fitness score of 0.994 and 0.996, respectively. When carefully considering the secondary structures of all 30 optimal RNAs of models N01 and N02 obtained by the tool, it was found that the design errors causing imperfect fitness occurred at the internal loops of the hybridized RNAs. While the internal loop of model N01 was found to contain an extra base within the internal loop, model N02 had a missing internal loop. Thus, this design flaw should be subjected to further improvement of the tool such as the addition of a repair step as a part of the GA. Although iDoRNA did not provide a perfect design for models N01 and N02, the fitness scores were still very high, ensuring the highly stable structures, very similar in structure to their respective target models. Regarding the computational time, it should be noted that the time required to reach an optimum increases with the increasing complexity of the RNA-RNA interaction system. While requiring less than 7 s for designing models A01-A04, the tool needed about 22 and 25 s to provide the optimal designs for models N01 and N02, respectively. This is reasonable because the computational time required in the reproduction step is linearly dependent on the lengths of RNAs as well as the number of interacting domains. In conclusion, iDoRNA can efficiently design all 6 RNA-RNA interaction models with high fitness in short time.

3.3. Comparison of the Design Performance between iDoDe and iDoRNA

The design performances of iDoRNA was compared with iDoDe to see how much the GA helped increasing the performance in term of the designing accuracy as well as the computational time usage (

Table 3. Comparison of RNA design performance between iDoDeand iDoRNA.

Model No.	Time(s)	iDoRNA		iDoDe *		iDoDe **
		Optimal Fitness	Success Rate	Optimal Fitness	Success Rate	Time (s)	Optimal Fitness	Success Rate
A01	5	1.000	10/10	1.000	1/28	177	1.000	7/1000
A02	5	1.000	10/10	1.000	1/31	173	1.000	42/1000
A03	6	1.000	10/10	0.875	0/23	237	0.922	0/1000
A04	6	1.000	10/10	0.938	0/22	301	0.968	0/1000
N01	17	1.000	10/10	0.949	0/86	495	0.967	0/1000
N02	21	0.996	0/10	0.934	0/54	252	0.881	0/1000

* iDoDe was performed using the same computational time as iDoRNA. ** iDoDe was performed for 1000 runs.

). The six artificial RNA-RNA interaction models were used as the targets. For a fair comparison, we compared the design accuracy of the RNA solutions obtained from the two tools with the same computational time. In doing so, we used the total time required to run iDoRNA for each RNA model as the termination criterion for the iDoDerun. The values of the GA parameters used were the same as those in the previous section. The design results are summarized in Table 3.

It is obvious that iDoRNA performed much better than iDoDe for all test models. The optimal RNA individuals provided by iDoRNA for all models were almost ideal, and only failed to reach the fitness score of 1 for model N02. The success rate also indicates the design power of iDoRNA against iDoDe. It should be noted is that while iDoRNA can provide a perfect design with a 100% success rate for five out of the six models, iDoDe does not provide a perfect solution for models A03-A04 and N01-N02, mainly due to the random nature of the iDoDe design. Apparently, the RNA solutions obtained from iDoDe did not have maximum fitness, thus they might yield unstable and dissimilar structures with their target RNA-RNA interaction, especially, at the required bulges and internal-loops of HR. Additionally, we repeatedly found was unwanted hairpin-loops on linear segments in the cases of models N01 and N02. Therefore, with incorporation of GA in iDoRNA, we could overcome these problems of iDoDe. Furthermore, instead of fixing the time, we attempted to run iDoDe for 1000 trials to see if we could obtain a successful design for each model. It was clearly demonstrated that iDoDe still fails to provide a perfect design for models A03-A04 and N01-N02 (

Table 4. Comparison of features between iDoRNA and the other tools for designing RNA-RNA interaction.

Features		NUPACK	RNAiFold 2.0	RiboMaker	iDoRNA
Service:
Source code		C	C++	C++	C
Web server		✓	✓	✓	✗
Input:
Target structures:	Single stranded RNA	✓ (Web server); ✗ (Source code)	✗	✓	✓
	Hybridized RNA	✓	✓	✓	✓
Constrained sequences		✓	✓	✓	✓
IUPAC codes		IUPAC codes	IUPAC codes	A C G U N	IUPAC codes
Pseudo-knot		✗	✗	✗	✗
Specification:
Folding temperature		✓	✓	✗	✓
GC-content		✓	✓	✗	✓
Consecutive nucleotides prevention		✓	✓	✗	✗
Solution per run		✓	✓	✗	✗
Alternative energy parameters		✓	✗	✗	✗
Output:
Designed sequences		≥ 2 strands (Web server) 2 strands (Source code)	2 strands	2 strands	2 strands
Predicted structures	Dot-bracket or Dot-plus-parentheses notation	✓	✓	✓	✓
	Graphical structure	✗	✓	✓	✓
Design method:
Design objective		min ensemble defect	Constraint-based	min Fobj	max Fitness
Decomposition		Hierarchical Structure decomposition	Tree-like decomposition	✗	Interacting domain-based decomposition
Optimization*		EO	CP, LNS	MCSA	GA
Folding prediction		NUPACK	RNAcofold	RNAfold, RNAup	RNAfold, RNAcofold

* List of optimization methods are ensemble defect optimization (EO), constraint-based programing (CP), large neighborhood search (LNS), Monte Carlo simulated annealing (MCSA), and genetic algorithm (GA).

). It can be concluded that iDoRNA can give more accurate RNA solutions in a shorter time for any RNA-RNA interaction based system. Thus, this shall be a promising tool for designing RNA-RNA interaction systems for synthetic biology applications.

3.4. Comparison of the Design Performance between iDoRNA with the other Design Tools

In this section, we compared the differences of the existing features between iDoRNA with other published tools; i.e., NUPACK, RNAiFold 2.0, and RiboMaker (Table 4). Then, we benchmarked the design performance of our tool against these benchmark tools using different criteria (

Table 5. Comparison of RNA design performance between iDoRNA and the other RNA structural design tools on 44 models.

HR-length/# of ID	Model No.	Average Ensemble Defect				Average Fitness Score
		NUPACK	RNAiFold	RiboMaker	iDoRNA	NUPACK	RNAiFold	RiboMaker	iDoRNA
Actual models
102-212/ 17-35	N01-07	0.00-0.02	0.02-0.07	0.60-0.84	0.05-0.18	N/A	N/A	0.18-0.44	0.90-1.00
Artificial models
10-49/ 3-11	A01-06	0.01-0.03	0.01-0.19	0.64-0.79	0.02-0.21	N/A	N/A	0.14-0.87	0.94-1.00
50-99/ 12-20	A07-16	0.00-0.01	0.01-0.19	0.67-0.86	0.05-0.21	N/A	N/A	0.34-0.66	0.92-1.00
100-149/ 6-30	A17-28	0.00-0.02	0.00-0.09	0.64-0.81	0.00-0.28	N/A	N/A	0.34-0.87	0.87-0.99
150-199/ 22-51	A29-35	0.00-0.02	0.01-0.08	0.54-0.76	0.00-0.31	N/A	N/A	0.24-0.57	0.87-0.99
200-250/ 22-30	A36-37	0.01-0.04	0.01-0.02	0.64-0.59	0.10-0.18	N/A	N/A	0.43-0.44	0.95-0.98

).

In order to explore different features between our tool and the other tools, we categorized all features into five groups: service, input, specification, output, and design method as shown in Table 4, the details of which are described as follows:

Service

Source codes of all tools are available for download. For tool development, NUPACK and iDoRNA are developed on C programming language whereas RNAiFold 2.0 and RiboMaker are implemented with C++. In the current version, iDoRNA does not provide a design service on web server, whereas the others are available.

Input

Among the four design tools, NUPACK source code version and RNAiFold 2.0 allow only one target structure to be used as an input whereas RiboMaker and iDoRNA are able to receive inputs of single-stranded RNAs and hybridized RNA. In addition, all design tools allow users to constrain specific bases with all IUPAC codes, except for RiboMaker that allows the specification with only A C G U N bases. Unfortunately, all tools do not handle a pseudo-knot structure as the input.

Specification

We collected the features of this part which have been done on the available web server services of NUPACK, RNAiFold 2.0 and RiboMaker to compare with our current tool’s abilities (source code version). NUPACK, RNAiFold 2.0 and iDoRNA allow users to specify GC-content, and folding temperature. For specific purposes, NUPACK and RNAiFold 2.0 provide an option for consecutive nucleotides prevention. Moreover, NUPACK includes alternative energy parameters for calculation of structural energy. It was noted that RiboMaker does not provide any features in this category.

Output

All four tools provide a set of two designed RNA sequences as output. However, NUPACK on the web server is able to design more than two RNA strands which interact with each other. Also, all the tools give the results of predicted structure(s) in dot-bracket (or dot-plus-parentheses in NUPACK) structures and a graphical structure by different visualization methods (NUPACK by NUPACK [13], RNAiFold 2.0 and RiboMaker by VARNA [61], and iDoRNA by RNAfold 2.0 and RNAcofold [52]).

Design Method

During the initialization step, NUPACK, RNAiFold 2.0, and iDoRNA separate the target structures into substructures by different decomposition methods before sequence generation. On the contrary, RiboMaker generates the random sequences of all structures without a decomposition step. Among optimization methods, only constraint-based programing (CP) used in RNAiFold 2.0 is a non-heuristic method which designs sequences based on defined constraints, whereas the other methods are based on a heuristic method. All the tools, except for NUPACK which uses its own prediction method, use additional methods from Vienna RNA package [52] for predicting a possible structure of the designed sequences.

To benchmark our tool with the other existing tools, forty-four test models containing different lengths and characteristics of secondary structural elements (Supplementary Data S1) were designed. Among these test models, N01-N07 are models built from the reported structures of previous laboratory experiments, which represent actual RNA-RNA interaction; A01-A04 are simple artificial models representing the classical secondary structural elements: unpaired nucleotides, paired bases, and hairpin loops; and A05-A37 are the artificial models built from structural RNA sets. In this work, we compared the performance of iDoRNA with NUPACK, RNAiFold 2.0 and RiboMaker using the same computational environment. To avoid inverse folding times in large and complex structures, we used RNAiFold 2.0 with a Large Neighborhood Search (LNS) method, and set the time constraint of each run to within 2 hours. Criteria for comparison include ensemble defects, fitness scores and computational times. Note that the fitness score was used as the criterion to compare the performance between RiboMaker and iDoRNA only. This is because F score could not be determined due to the unavailability of secondary structures of R1 and R2 provided by NUPACK and RNAiFold 2.0. The results of interacting domain patterns from each test model obtained from the interacting domain-based decomposition algorithm is shown in Supplementary Data S3, while the best design results for all test models from iDoRNA is reported in Supplementary Data S4. The performance comparison between these design tools is shown in Table 5 and Supplementary Data S5 which are discussed as follows.

Firstly, Table 5 shows that when using ensemble defects as the criteria, NUPACK outperforms RNAiFold 2.0, RiboMaker and iDoRNA in designing all 44 test models. The ensemble defect results indicate that all designed RNA sequences from NUPACK are able to fold into the HR structures with less average number of incorrectly paired nucleotides at equilibrium than those of the other tools. This is not surprising because the design objective of NUPACK is to minimize the ensemble defects [13] while RNAiFold 2.0 and iDoRNA use other different objectives (Table 4). Secondly, while NUPACK and RNAiFold 2.0 require HR as input, both RiboMaker and iDoRNA require input containing a set of R1, R2 and HR. Thus, it is noteworthy to carefully consider the performance differences between iDoRNA with RiboMaker. When using ensemble defect as the criterion, we found that iDoRNA shows better performance than RiboMaker in designing all test models. Furthermore, it is seen that iDoRNA also outperforms RiboMaker when considering the F-score as the criterion. This is because the objective function of RiboMaker includes the energies of hybridization region, individual RNA structures, and hamming distance, and it does not allow the specification of all single-stranded structures [29] which could lead to a lower similarity and thus the fitness score. On the contrary, the objective function of iDoRNA is to maximize the fitness score which is formulated from two RNA properties; i.e., structural similarity and stability Nevertheless, it can also be seen that iDoRNA could only provide the designs with a perfect F score (F = 1) for all four simple models (A01-A04), but not for the actual and the remaining artificial models (Supplementary Data S5). Finally, when considering the computational time, it is shown that the performance of iDoRNA is better than RiboMaker but worse than NUPACK and RNAiFold 2.0 (See Supplementary Data S5).

4. Conclusions

In this study, we have proposed a new computational tool named iDoRNA for designing RNA sequences of a given RNA-RNA interaction. This tool employed a domain-based decomposition algorithm to decompose input RNAs into interacting domains as well as a genetic algorithm (GA) as an optimization tool to search for an optimal set of RNA-RNA interactions. We used a fitness function derived from the structural similarity between designed and target RNAs, and the MFE of hybridized RNA as the design objective. For the best design, we suggested ω_sim of 0.7, Cr of 0.9, Mr of 0.1, n of 8 individual per population as the optimal design parameters that provide optimal RNA-RNA interactions with the shortest computational time. Given a set of RNA-RNA interaction models with various structural complexities, we demonstrated that iDoRNA was able to efficiently design sequences of two RNA molecules that can form exact structures at both intramolecular and intermolecular states of the target models. For design performance, we showed that iDoRNA performed markedly better than our previously published iDoDe as it can design multi-state RNAs of all models with higher fitness in less computational time. In addition, we also showed that iDoRNA performed relatively well when compared with other established design tools. Thus, with the use of GA as heuristic optimization, iDoRNA represents an alternative powerful tool for designing RNA-RNA interaction as a novel device in synthetic biology.

However, iDoRNA still has some drawbacks, which are topics for further research. Firstly, it still fails to properly design some secondary structural elements that are present in hybridized RNAs. Secondly, it only designs sequences of RNA-RNA interaction with the desired secondary structures. Thirdly, the current version of iDoRNA is not yet capable of designing RNA-RNA interactions containing more than two RNA molecules. Fourthly, additional optimization criteria (i.e., ensemble defects and base pair distances), as well as input specifications (i.e., consecutive nucleotides prevention should be provided as user options). Furthermore, this design tool may prove beneficial to biologists and other potential users in the form of a web interface. With these future improvement, iDoRNA could become an even more powerful tool for the development of the novel RNA devices in synthetic biology.