Novel Criteria for Deterministic Remote State Preparation via the Entangled Six-Qubit State
Abstract
:1. Introduction
2. Related Works
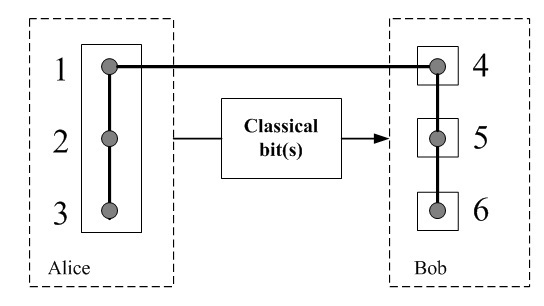
3. Remote State Preparation of an Arbitrary Three-Particle State
3.1. The Coefficients Are Real
3.2. The Coefficients Are Complex
- (i)
- ,
- (ii)
- ,
- (iii)
- ,
- (iv)
- .
4. Remote State Preparation of an Arbitrary N-Particle State
- (1)
- The normalization condition,
- (2)
- .
5. Classical Communication Cost
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
| SN | Special Type | Permutation | Norm, Phase Factor | BAUO | Example |
|---|---|---|---|---|---|
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 |
References
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein–Podolsky–Rosen channels. Phys. Rev. Lett. 1993, 70, 1895–1899. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.Y.; Chen, X.B.; Luo, M.X.; Zhang, R.; Yang, Y.X. Remote preparation of a four-particle entangled cluster-type state. Opt. Commun. 2011, 284, 4088–4093. [Google Scholar] [CrossRef]
- Barreiro, J.T.; Wei, T.C.; Kwiat, P.G. Remote preparation of single-photon “hybrid” entangled and vector-polarization states. Phys. Rev. Lett. 2010, 105, 030407. [Google Scholar] [CrossRef] [PubMed]
- Zhou, N.R.; Cheng, H.L.; Tao, X.Y.; Gong, L.H. Three-party remote state preparation schemes based on entanglement. Quantum Inf. Process. 2014, 13, 513–526. [Google Scholar] [CrossRef]
- Lo, H.K. Classical-communication cost in distributed quantum-information processing: A generalization of quantum-communication complexity. Phys. Rev. A 2000, 62, 012313. [Google Scholar] [CrossRef]
- Pati, A.K. Minimum classical bit for remote preparation and measurement of a qubit. Phys. Rev. A. 2000, 63, 014302. [Google Scholar] [CrossRef]
- Leung, D.W.; Shor, P.W. Oblivious remote state preparation. Phys. Rev. Lett. 2003, 90, 127905. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.X.; Chen, X.B.; Ma, S.Y.; Niu, X.X.; Yang, Y.X. Joint remote preparation of an arbitrary three-qubit state. Opt. Commun. 2010, 283, 4796–4801. [Google Scholar] [CrossRef]
- Zhan, Y.B.; Hu, B.L.; Ma, P.C. Joint remote preparation of four-qubit cluster-type states. J. Phys. B At. Mol. Opt. Phys. 2011, 44, 095501. [Google Scholar] [CrossRef]
- Fu, H.; Chen, G.-B.; Li, X.-W.; Ma, P.-C.; Zhan, Y.-B. Joint remote preparation of an arbitrary four-qubit x-type entangled state. 2016; arXiv:1605.05446. [Google Scholar]
- Chen, X.-B.; Ma, S.-Y.; Su, Y.; Zhang, R.; Yang, Y.-X. Controlled remote state preparation of arbitrary two and three qubit states via the brown state. Quantum Inf. Process. 2012, 11, 1653–1667. [Google Scholar] [CrossRef]
- Liu, L.L.; Hwang, T. Controlled remote state preparation protocols via aklt states. Quantum Inf. Process. 2014, 13, 1639–1650. [Google Scholar] [CrossRef]
- Gao, C.; Ma, S.-Y.; Chen, W.-L. Controlled remote preparation via the brown state with no restriction. Int. J. Theor. Phys. 2016, 55, 2643–2652. [Google Scholar] [CrossRef]
- Li, J.-F.; Liu, J.-M.; Feng, X.-L.; Oh, C.H. Deterministic remote two-qubit state preparation in dissipative environments. Quantum Inf. Process. 2016, 15, 2155–2168. [Google Scholar] [CrossRef]
- Wang, H.-B.; Zhou, X.-Y.; An, X.-X.; Cui, M.-M.; Fu, D.-S. Deterministic joint remote preparation of a four-qubit cluster-type state via GHZ states. Int. J. Theor. Phys. 2016, 55, 3588–3596. [Google Scholar] [CrossRef]
- Killoran, N.; Biggerstaff, D.N.; Kaltenbaek, R.; Resch, K.J.; Lütkenhaus, N. Derivation and experimental test of fidelity benchmarks for remote preparation of arbitrary qubit states. Phys. Rev. A. 2010, 81, 012334. [Google Scholar] [CrossRef]
- Rådmark, M.; Wieśniak, M.; Żukowski, M.; Bourennane, M. Experimental multilocation remote state preparation. Phys. Rev. A 2013, 88, 032304. [Google Scholar] [CrossRef]
- Xia, Z.; Wang, X.; Sun, X.; Wang, Q. A secure and dynamic multi-keyword ranked search scheme over encrypted cloud data. IEEE Trans. Parallel Distrib. Syst. 2015, 27, 340–352. [Google Scholar] [CrossRef]
- Zhangjie, F.; Xingming, S.; Qi, L.; Lu, Z.; Jiangang, S. Achieving efficient cloud search services: Multi-keyword ranked search over encrypted cloud data supporting parallel computing. IEICE Trans. Commun. 2015, 98, 190–200. [Google Scholar]
- Ren, Y.; Shen, J.; Wang, J.; Han, J.; Lee, S. Mutual verifiable provable data auditing in public cloud storage. J. Internet Technol. 2015, 16, 317–323. [Google Scholar]
- Fu, Z.; Ren, K.; Shu, J.; Sun, X.; Huang, F. Enabling personalized search over encrypted outsourced data with efficiency improvement. IEEE Trans. Parallel Distrib. Syst. 2015. [Google Scholar] [CrossRef]
- Gu, B.; Sheng, V.S.; Tay, K.Y.; Romano, W.; Li, S. Incremental support vector learning for ordinal regression. IEEE Trans. Neural Netw. Learn. Syst. 2015, 26, 1403–1416. [Google Scholar] [PubMed]
- Zeng, B.; Zhang, P. Remote-state preparation in higher dimension and the parallelizable manifold Sn-1. Phys. Rev. A 2002, 65, 022316. [Google Scholar] [CrossRef]
- Liu, J.-M.; Feng, X.-L.; Oh, C. Remote preparation of arbitrary two- and three-qubit states. EPL 2009, 87. [Google Scholar] [CrossRef]
- Zhang, D.; Zha, X.-W.; Duan, Y.-J.; Wei, Z.H. Deterministic controlled bidirectional remote state preparation via a six-qubit maximally entangled state. Int. J. Theor. Phys. 2016, 55, 440–446. [Google Scholar] [CrossRef]
- Yan, F.-L.; Zhang, G.-H. Remote preparation of the two-particle state. Int. J. Quantum Inf. 2008, 6, 485–491. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Zhang, Z.J. Remote preparation of a class of three-qubit states. Opt. Commun. 2008, 281, 871–875. [Google Scholar] [CrossRef]
- Pan, G.X. Remote preparation of three-particle GHZ-class states. J. At. Mol. Sci. 2010, 1, 344–351. [Google Scholar] [CrossRef]
- Sheng, Y.-B.; Deng, F.-G. Deterministic entanglement purification and complete nonlocal bell-state analysis with hyperentanglement. Phys. Rev. A 2010, 81, 032307. [Google Scholar] [CrossRef]
- Zhan, Y.-B. Deterministic remote preparation of arbitrary two- and three-qubit states. EPL 2012, 98. [Google Scholar] [CrossRef]
- Wang, Z.-Y. Highly efficient remote preparation of an arbitrary three-qubit state via a four-qubit cluster state and an epr state. Quantum Inf. Process. 2013, 12, 1321–1334. [Google Scholar] [CrossRef]
- Ma, S.-Y.; Luo, M.-X. Efficient remote preparation of arbitrary two- and three-qubit states via the χ state. Chin. Phys. B. 2014, 23, 090308. [Google Scholar] [CrossRef]
- Borras, A.; Plastino, A.; Batle, J.; Zander, C.; Casas, M.; Plastino, A. Multiqubit systems: Highly entangled states and entanglement distribution. J. Phys. A Math. Theor. 2007, 40. [Google Scholar] [CrossRef]
- Choudhury, S.; Muralidharan, S.; Panigrahi, P.K. Quantum teleportation and state sharing using a genuinely entangled six-qubit state. J. Phys. A Math. Theor. 2009, 42, 115303. [Google Scholar] [CrossRef]
- Zha, X.-W.; Song, H.-Y. Two schemes of remote preparation of a four-particle entangled w state via a six-qubit maximally entangled state. Phys. Scr. 2011, 84, 015010. [Google Scholar] [CrossRef]
- Li, C.-C.; Nie, Y.-Y.; Shag, M.-H. Quantum state sharing of an arbitrary single qubit state by using a genuinely entangled sixqubit state as a quantum channel. J. Jiangxi Nomal Univ. 2012, 36, 267–270. (In Chinese) [Google Scholar]
- Sun, X.-M.; Zha, X.-W. A scheme of bidirectional quantum controlled teleportation via six-qubit maximally entangled state. Acta Photonica Sin. 2013, 42, 1052–1056. [Google Scholar]
- Sun, Z.; Zhang, C.; Wang, P.; Yu, J.; Zhang, Y.; Long, D. Multi-party quantum key agreement by an entangled six-qubit state. Int. J. Theor. Phys. 2016, 55, 1920–1929. [Google Scholar] [CrossRef]


| AMR123 | The State on the Particles 4, 5, 6 | BAUO | |
|---|---|---|---|
| 000 | |||
| 001 | |||
| 010 | |||
| 011 | |||
| 100 | |||
| 101 | |||
| 110 | |||
| 111 |
| AMR123 | The State on the Particles 4, 5, 6 | BAUO | |
|---|---|---|---|
| 000 | |||
| 001 | |||
| 010 | |||
| 011 | |||
| 100 | |||
| 101 | |||
| 110 | |||
| 111 |
| Zha’s Protocol [35] | Our Protocol | |
|---|---|---|
| Entanglement resource | Entangled six-qubit state | Entangled six-qubit state |
| Prepared state | Four-particle W state | Arbitrary three-particle state |
| The number of parameters | 4 | 8 |
| Qubits | 6 | 6 |
| Cbits | 2 | 3 |
| Qubit efficiency | 100% | 100% |
| Success probability | 100% (Non-deterministic) | 100% (Deterministic) |
| Recovery operation | U | Pauli operations |
| Entanglement Resource | Qubits | Cbits(General Case) | Success Probability | |
|---|---|---|---|---|
| Zhan’s protocol [30] | Three GHZ states | 9 | 6 | 100% |
| Wang’s protocol [31] | Four-qubit cluster state + EPR pair | 6 | 3 | 50% |
| Ma’s protocol [32] | state | 6 | 4 | 50% |
| Our protocol | Entangled Six-qubit state | 6 | 3 | 100% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Chen, X.-B.; Dou, Z.; Li, J.; Liu, X.; Li, Z. Novel Criteria for Deterministic Remote State Preparation via the Entangled Six-Qubit State. Entropy 2016, 18, 267. https://doi.org/10.3390/e18070267
Xu G, Chen X-B, Dou Z, Li J, Liu X, Li Z. Novel Criteria for Deterministic Remote State Preparation via the Entangled Six-Qubit State. Entropy. 2016; 18(7):267. https://doi.org/10.3390/e18070267
Chicago/Turabian StyleXu, Gang, Xiu-Bo Chen, Zhao Dou, Jing Li, Xin Liu, and Zongpeng Li. 2016. "Novel Criteria for Deterministic Remote State Preparation via the Entangled Six-Qubit State" Entropy 18, no. 7: 267. https://doi.org/10.3390/e18070267
APA StyleXu, G., Chen, X. -B., Dou, Z., Li, J., Liu, X., & Li, Z. (2016). Novel Criteria for Deterministic Remote State Preparation via the Entangled Six-Qubit State. Entropy, 18(7), 267. https://doi.org/10.3390/e18070267