4.1. Standard Problem Solution
The control rod insertion positions shown in
Figure 2 were chosen as the standard and reference solution. This example solution is the basis of the optimization. The neutron diffusion equations and heat transfer equations are all solved by FVM. In each calculation, the considered domain is one quarter of the whole core with reflective and non-return external boundaries. The convergence criterion is set as maximum relative flux change on each inner iteration = 10
−10, maximum
keff change on outer iteration = 10
−6. Four groups of regular hexahedral meshes are taken into consideration. The mesh quantities and calculation results are given in
Table 3. The error in
Table 3 represents the relative error between using a mesh group and its further refinement.
Considering both of the calculation accuracy and time cost, mesh No. 2 was selected to be applied for the next optimization scheme. This quantity of mesh is also used in [
36], thus our neutron diffusion calculation results can be checked. The calculated
keff is 1.02855 and the reference at the same mesh quantity is 1.02864, with the difference of 0.0087%. The results of fast and thermal neutron flux at the diagonal line on the
x-
y plane at the level of
z = 195 cm are plotted in
Figure 3 and
Figure 4. A good match between calculated results and references can be seen.
The calculation local power, temperature and entropy production results are plotted in
Figure 5,
Figure 6 and
Figure 7. It can be seen in
Figure 5 that the control rods have an obvious effect on the neutron fission power. Both the vertical and horizontal cross sections show significant decreases of local power depending on the control rod positions. The comparison of horizontal cross section at different
z levels shows that the local power near the center of the core is higher than at the upper level, as expected.
Figure 6 shows that the regular temperature distribution is not as complex as the fission power distribution. It shows a continuous reduce from the core center to the edge. The control rod positions cannot be seen clearly in these temperature cloud pictures. The regular local entropy production distribution is far from the temperature distribution.
Figure 7 shows that the boundary centers of the reactor core are the peaks of the local entropy production, and the volume center of the reactor core is the valley of the local entropy production. The reason is that this core is symmetric at the vertical middle cross section, thus the middle cross section is heat insulated and the temperature gradient there is zero. The rapid decrease of temperature near the boundary center causes the entropy production peak.
In total, some lumped and feature parameters are selected to describe the thermal situation of the reactor core. These parameters are the power peak factor
Pmax, the maximum temperature
Tmax and the total entropy production
Stot. These parameters’ values are shown in
Table 4.
4.2. Response Surface Design
The BBD is introduced to apply the RSM. The insert positions of control rods
Z1,
Z2,
Z3,
Z4 are the input independent variables, and the feature parameters
Pmax,
Tmax,
Stot are chosen as the response variables. The RSM can be written as follows:
where:
In order to establish the coefficient matrix
b, several experiments should be performed.
Section 4.1 presents an example of a numerical experiment. The input variables are [
Z1 Z2 Z3 Z4] = [202802020], and the response result
Y is given in
Table 4. Using BBD to design the RSM for this problem, 29 groups of numerical experiments must be executed. The input and response variables are shown in
Table 5. The matrix
b is obtained by Equation (17) and the fitting results are shown in
Table 6.
The fitting results are usually evaluated by R-square. For this evaluation index, the closer to 1, the better result gained. The R-square value of the three response surface fitting is shown in
Table 7.
It can be seen in
Table 7 that, although
Tmax is a local feature, depending on its simple regular distribution, the R-square of its response surface is the highest. The second is
Stot since it is a total summary of local entropy production. It has the both global and local parameter features, so its sensitivity to the input variables is weaker than that of the local parameter. The R-square of the
Pmax response surface is not as fine as the others, due to the complex local power distribution. As these response surfaces are introduced to find out the direction of optimization, rather than obtain the exact solution, this level of fitting can also be applied.
4.3. Rod Position Optimization
In this section, a simple code is programmed to traverse all four input variable ranges in the definition domain, which is set as [30 cm, 300 cm]. The coefficients in
Table 6 and Equation (18) are used in this code to obtain the approximate response results. The interval step of the input variables is set as 10 cm. In every traversal calculation, one evaluation index (
Pmax,
Tmax or
Stot) is selected as the optimization direction. The aim of optimization is to promote safety or reduce entropy dissipation, that is to say,
Pmax,
Tmax or
Stot should be reduced.
Although these three indexes are key metrics for a reactor core, the importance rankings are not at the same level for each of them. For every nuclear energy system, safety is always a seriously concerned for the public [
42], and its status is higher than economical efficiency.
Tmax is the most obvious safety index, as the reactor materials may melt above a certain temperature limit, which would cause a serious accident.
Pmax is also a type of safety index, which is associated with the level of power flattening. A more flattened power distribution means a smoother reactor operation is expected. The last is the economical index
Stot, which represents the energy dissipation.
Therefore, our optimization procedure is: (1) use RSM to traverse all the control rod positions to find
N1 positions approaching the lowest
Tmax. The selected positions are put in set Ω
1; (2) Use RSM again to traverse all the positions in the definition domain to find
N2 positions approaching the lowest
Pmax and name the selected positions set as Ω
2; (3) Use FVM to obtain accurate indexes of position elements in Ω
3, Ω
3 = Ω
1 ∩ Ω
2, and sort them by
Stot. The best solution is chosen as the final optimization scheme. The flow diagram of this optimization procedure is shown in
Figure 8.
In this scheme, a smaller
N1 or
N2 means a narrower search range, but the indexes may become closer to the limit. In this case, they are set as
N1 =
N2 = 10. Finally, eight groups of control rod positions are selected, which are listed in
Table 8.
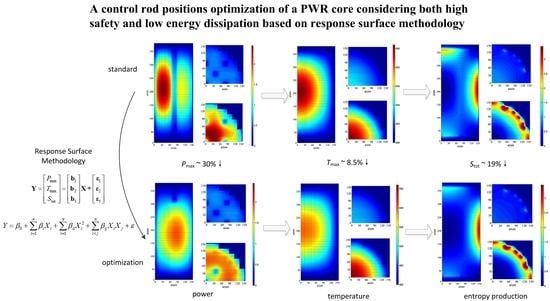
It can be seen in
Table 8 that the safety and entropy index will reach optimization when the central control rods are inserted deeply and the peripheral control rods are inserted shallowly. In the calculation series, it can be found that when the input rod positions are [30 30 300 300], the
Pmax,
Tmax and
Stot reach the minimum, which means that both the power and temperature are flatter, and the energy dissipation reaches the minimum. In order to observe the physical field in depth, the distributions of local power, temperature and local entropy production are illustrated in
Figure 9,
Figure 10 and
Figure 11.
The cloud pictures
Figure 9 and
Figure 11 share the same colorbar scale as
Figure 5,
Figure 6 and
Figure 7, respectively. Thus the differences between these two groups can be clearly observed. Comparing
Figure 9 with
Figure 5, it can be found that the power flattening effect is better after the control rod adjustment. The central control rod has an obvious influence on the power distribution, which causes a power valley at the core center, so the temperature at the center line of
x =
y = 0, is not so high as the temperature in the standard problem, which can be seen in
Figure 6 and
Figure 10. The distribution of local entropy production is similar between
Figure 7 and
Figure 11, but the entropy production values are reduced after control rod adjustment.
In order to show some details of the optimization results, the local power, temperature and local entropy production at the diagonal line on midplane are shown in
Figure 12. It can be seen in
Figure 12a that the local power decreases near the core center and a power valley forms between the distance of 40 cm and 50 cm, as the control rods in FA.1 and FA.18 are inserted deeply. At the same time, with the control rods in FA.5 and FA.31 rise, the local power of the optimization scheme is higher than that of the standard problem in the distance range of [65 cm, 110 cm]. As a result, local power is flatter than in the standard problem and the power peak factor is reduced. For the temperature distribution, as shown in
Figure 12b, the temperature and its gradient are reduced near the core center while a little increase is noted near the core boundary, which matches the local power distribution. The change of temperature gradient causes a lower local entropy production near the core center and the one higher near the core boundary, which is shown in
Figure 12c.
As a result, the evaluation indexes of the standard problem and optimization scheme are listed in
Table 9. An obvious decrease can be seen, which is satisfactory for the optimization.