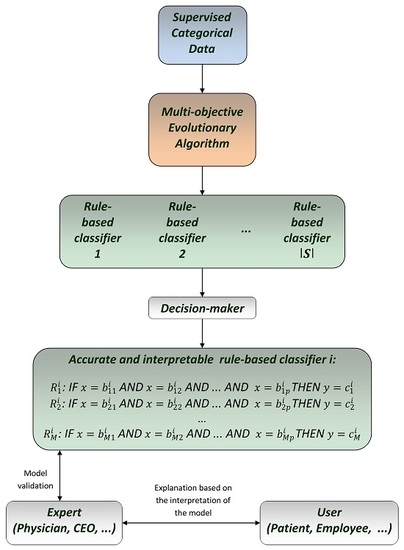
Multi-Objective Evolutionary Rule-Based Classification with Categorical Data

Abstract

The ease of interpretation of a classification model is essential for the task of validating it. Sometimes it is required to clearly explain the classification process of a model’s predictions. Models which are inherently easier to interpret can be effortlessly related to the context of the problem, and their predictions can be, if necessary, ethically and legally evaluated. In this paper, we propose a novel method to generate rule-based classifiers from categorical data that can be readily interpreted. Classifiers are generated using a multi-objective optimization approach focusing on two main objectives: maximizing the performance of the learned classifier and minimizing its number of rules. The multi-objective evolutionary algorithms ENORA and NSGA-II have been adapted to optimize the performance of the classifier based on three different machine learning metrics: accuracy, area under the ROC curve, and root mean square error. We have extensively compared the generated classifiers using our proposed method with classifiers generated using classical methods such as PART, JRip, OneR and ZeroR. The experiments have been conducted in full training mode, in 10-fold cross-validation mode, and in train/test splitting mode. To make results reproducible, we have used the well-known and publicly available datasets Breast Cancer, Monk’s Problem 2, Tic-Tac-Toe-Endgame, Car, kr-vs-kp and Nursery. After performing an exhaustive statistical test on our results, we conclude that the proposed method is able to generate highly accurate and easy to interpret classification models.

1. Introduction

Supervised Learning is the branch of Machine Learning (ML) [1] focused on modeling the behavior of systems that can be found in the environment. Supervised models are created from a set of past records, each one of which, usually, consists of an input vector labeled with an output. A supervised model is an algorithm that simulates the function that maps inputs with outputs [2]. The best models are those that predict the output of new inputs in the most accurate way. Thanks to modern computing capabilities, and to the digitization of ever-increasing quantities of data, nowadays, supervised learning techniques play a leading role in many applications. The first classification systems date back to the 1990s; in those days, researchers were focused on both precision and interpretability, and the systems to be modeled were relatively simple. Years later, when it became necessary to model more difficult behaviors, the researchers focused on developing more and more precise models, leaving aside the interpretability. Artificial Neural Networks (ANN) [3], and, more recently, Deep Learning Neural Networks (DLNN) [4], as well as Support Vector Machines (SVM) [5], and Instance-based Learning (IBL) [6] are archetypical examples of this approach. A DLNN, for example, is a large mesh of ordered nodes arranged in a hierarchical manner and composed of a huge number of variables. DLNNs are capable of modeling very complex behaviors, but it is extremely difficult to understand the logic behind their predictions, and similar considerations can be drawn for SVNs and IBLs, although the underlying principles are different. These models are known as black-box methods. While there are applications in which knowing the ratio behind a prediction is not necessarily relevant, (e.g., predicting a currency’s future value, whether or not a user clicks on an advert or the amount of rain in a certain area), there are other situations where the interpretability of a model plays a key role.

The interpretability of classification systems refers to the ability they have to explain their behavior in a way that is easily understandable by a user [7]. In other words, a model is considered interpretable when a human is able to understand the logic behind its prediction. In this way, Interpretable classification models allow external validation by an expert. Additionally, there are certain disciplines such as medicine, where it is essential to provide information about decision making for ethical and human reasons. Likewise, when a public institution asks an authority for permission to investigate an alleged offender, or when the CEO of a certain company wants to take a difficult decision which can seriously change the direction of the company, some kind of explanations to justify these decisions may be required. In these situations, using transparent (also called grey-box) models is recommended. While there is a general consensus on how the performance of a classification system is measured (popular metrics include accuracy, area under the ROC curve, and root mean square error), there is no universally accepted metric to measure the interpretability of the models. Nor is there an ideal balance between the interpretability and performance of classification systems but this depends on the specific application domain. However, the rule of thumb says that the simpler a classification system is, the easier it is to interpret. Rule-based Classifiers (RBC) [8,9] are among the most popular interpretable models, and some authors define the degree of interpretability of an RBC as the number of its rules or as the number of axioms that the rules have. These metrics tend to reward models with fewer rules as simple as possible [10,11]. In general, RBCs are classification learning systems that achieve a high level of interpretability because they are based on a human-like logic. Rules follow a very simple schema:

IF (Condition 1) and (Condition 2) and … (Condition N) THEN (Statement)

and the fewer rules the models have and the fewer conditions and attributes the rules have, the easier it will be for a human to understand the logic behind each classification. In fact, RBCs are so natural in some applications that they are used to interpret other classification models such as Decision Trees (DT) [12]. RBCs constitute the basis of more complex classification systems based on fuzzy logic [13] such as LogitBoost or AdaBoost [14].

Our approach investigates the conflict between accuracy and interpretability as a multi-objective optimization problem. We define a solution as a set of rules (that is, a classifier), and establish two objectives to be maximized: interpretability and accuracy. We decided to solve this problem by applying multi-objective evolutionary algorithms (MOEA) [15,16] as meta-heuristics, and, in particular, two known algorithms: NSGA-II [15] and ENORA [17]. They are both state-of-the-art evolutionary algorithms which have been applied, and compared, on several occasions [18,19,20]. NSGA-II is very well-known and has the advantage of being available in many implementations, while ENORA generally has a higher performance. In the current literature, MOEAs are mainly used for learning RBCs based on fuzzy logic [18,21,22,23,24,25,26]. However, Fuzzy RBCs are designed for numerical data, from which fuzzy sets are constructed and represented by linguistic labels. In this paper, on the contrary, we are interested in RBCs for categorical data, for which a novel approach is necessary.

This paper is organized as follows. In Section 2, we introduce multi-objective constrained optimization, the evolutionary algorithms ENORA and NSGA-II, and the well-known rule-based classifier learning systems PART, JRip, OneR and ZeroR. In Section 3, we describe the structure of an RBC for categorical data, and we propose the use of multi-objective optimization for the task of learning a classifier. In Section 4, we show the result of our experiments, performed on the well-known publicly accessible datasets Breast Cancer, Monk’s Problem 2, Tic-Tac-Toe-Endgame, Car, kr-vs-kp and Nursery. The experiments allow a comparison among the performance of the classifiers learned by our technique against those of classifiers learned by PART, JRip, OneR and ZeroR, as well as a comparison between ENORA and NSGA-II for the purposes of this task. In Section 5, the results are analyzed and discussed, before concluding in Section 6. Appendix A and Appendix B show the tables of the statistical tests results. Appendix C shows the symbols and the nomenclature used in the paper.

2. Background

2.1. Multi-Objective Constrained Optimization

The term optimization [27] refers to the selection of the best element, with regard to some criteria, from a set of alternative elements. Mathematical programming [28] deals with the theory, algorithms, methods and techniques to represent and solve optimization problems. In this paper, we are interested in a class of mathematical programming problems called multi-objective constrained optimization problems [29], which can be formally defined, for l objectives and m constraints, as follows:

$$\begin{array}{ccc}Min./Max.\hfill & f_i\left(\mathbf{x}\right),\hfill & i=1,\dots ,l\hfill \\ subjectto\hfill & g_j\left(\mathbf{x}\right)\le 0,\hfill & j=1,\dots ,m\hfill \end{array}$$

(1)

where $f_i\left(\mathbf{x}\right)$ (usually called objectives) and $g_j\left(\mathbf{x}\right)$ are arbitrary functions. Optimization problems can be naturally separated into two categories: those with discrete variables, which we call combinatorial, and those with continuous variables. In combinatorial problems, we are looking for objects from a finite, or countably infinite, set $\mathcal{X}$, where objects are typically integers, sets, permutations, or graphs. In problems with continuous variables, instead, we look for real parameters belonging to some continuous domain. In Equation (1), $\mathbf{x}=\left\{x_1,x_2,\dots ,x_w\right\}\in {\mathcal{X}}^w$ represents the set of decision variables, where $\mathcal{X}$ is the domain for each variable $x_k$, $k=1,\dots ,w$.

Now, let $\mathcal{F}=\{\mathbf{x}\in {\mathcal{X}}^w|g_j\left(\mathbf{x}\right)\le 0,j=1,\dots ,m\}$ be the set of all feasible solutions to Equation (1). We want to find a subset of solutions $\mathcal{S}\subseteq \mathcal{F}$ called non-dominated set (or Pareto optimal set). A solution $\mathbf{x}\in \mathcal{F}$ is non-dominated if there is no other solution ${\mathbf{x}}^{\prime }\in \mathcal{F}$ that dominates $\mathbf{x}$, and a solution ${\mathbf{x}}^{\prime }$ dominates $\mathbf{x}$ if and only if there exists i ($1\le i\le l$) such that $f_i\left({\mathbf{x}}^{\prime }\right)$ improves $f_i\left(\mathbf{x}\right)$, and for every i ($1\le i\le l$), $f_i\left(\mathbf{x}\right)$ does not improve $f_i\left({\mathbf{x}}^{\prime }\right)$. In other words, ${\mathbf{x}}^{\prime }$ dominates $\mathbf{x}$ if and only if ${\mathbf{x}}^{\prime }$ is better than $\mathbf{x}$ for at least one objective, and not worse than $\mathbf{x}$ for any other objective. The set $\mathcal{S}$ of non dominated solutions of Equation (1) can be formally defined as:

$$\mathcal{S}=\left\{\mathbf{x}\in \mathcal{F}\mid \nexists {\mathbf{x}}^{\prime }({\mathbf{x}}^{\prime }\in \mathcal{F}\wedge \mathcal{D}\left({\mathbf{x}}^{\prime },\mathbf{x}\right))\right\}$$

where:

$$\mathcal{D}\left({\mathbf{x}}^{\prime },\mathbf{x}\right)=\exists i(1\le i\le l,f_i\left({\mathbf{x}}^{\prime }\right)<f_i\left(\mathbf{x}\right))\wedge \forall i(1\le i\le l,f_i\left({\mathbf{x}}^{\prime }\right)\le f_i\left(\mathbf{x}\right)).$$

Once the set of optimal solutions is available, the most satisfactory one can be chosen by applying a preference criterion. When all the functions $f_i$ are linear, then the problem is a linear programming problem [30], which is the classical mathematical programming problem and for which extremely efficient algorithms to obtain the optimal solution exist (e.g., the simplex method [31]). When any of the functions $f_i$ is non-linear then we have a non-linear programming problem [32]. A non-linear programming problem in which the objectives are arbitrary functions is, in general, intractable. In principle, any search algorithm can be used to solve combinatorial optimization problems, although it is not guaranteed that they will find an optimal solution. Metaheuristics methods such as evolutionary algorithms [33] are typically used to find approximate solutions for complex multi-objective optimization problems, including feature selection and fuzzy classification.

2.2. The Multi-Objective Evolutionary Algorithms ENORA and NSGA-II

The MOEA ENORA [17] and NSGA-II [15] use a $\left(\mu +\lambda \right)$ strategy (Algorithm 1) with $\mu =\lambda =popsize$, where $\mu$ corresponds to the number of parents and $\lambda$ refers to the number of children ($popsize$ is the population size), with binary tournament selection (Algorithm 2) and a rank function based on Pareto fronts and crowding (Algorithms 3 and 4). The difference between NSGA-II and ENORA is how the calculation of the ranking of the individuals in the population is performed. In ENORA, each individual belongs to a slot (as established in [34]) of the objective search space, and the rank of an individual in a population is the non-domination level of the individual in its slot. On the other hand, in NSGA-II, the rank of an individual in a population is the non-domination level of the individual in the whole population. Both ENORA and NSGA-II MOEAs use the same non-dominated sorting algorithm, the fast non-dominated sorting [35]. It compares each solution with the rest of the solutions and stores the results so as to avoid duplicate comparisons between every pair of solutions. For a problem with l objectives and a population with N solutions, this method needs to conduct $l·N·(N-1)$ objective comparisons, which means that it has a time complexity of $O(l·N^2)$ [36]. However, ENORA distributes the population in N slots (in the best case), therefore, the time complexity of ENORA is $O(l·N^2)$ in the worst case and $O(l·N)$ in the best case.

Algorithm 1$\left(\mu +\lambda \right)$ strategy for multi-objective optimization.

Require:$T>1$ {Number of generations} Require: $N>1$ {Number of individuals in the population}  1: Initialize P with N individuals  2: Evaluate all individuals of P  3: $t\leftarrow 0$  4: while$t<T$do  5:  $Q\leftarrow \varnothing$  6:  $i\leftarrow 0$  7:  while $i<N$ do  8:   Parent1← Binary tournament selection from P  9:   Parent2← Binary tournament selection from P 10:   Child1, Child2←Crossover(Parent1, Parent2) 11:   Offspring1←Mutation(Child1) 12:   Offspring2←Mutation(Child2) 13:   Evaluate Offspring1 14:   Evaluate Offspring2 15:   $Q\leftarrow Q\bigcup \left\{\mathit{Offspring}\mathit{1},\mathit{Offspring}\mathit{2}\right\}$ 16:   $i\leftarrow i+2$ 17:  end while 18:  $R\leftarrow P\bigcup Q$ 19:  $P\leftarrow$N best individuals from R according to the rank-crowding function in population R 20:  $t\leftarrow t+1$ 21: end while 22: return Non-dominated individuals from P

Algorithm 2 Binary tournament selection.

Require:P {Population}  1: $I\leftarrow$ Random selection from P  2: $J\leftarrow$ Random selection from P  3: ifI is better than J according to the rank-crowding function in population P then  4:  return I  5: else  6:  return J  7: end if

Algorithm 3 Rank-crowding function.

Require:P {Population} Require: $I,J$ {Individuals to compare}  1: if$rank\left(P,I\right)<rank\left(P,J\right)$then  2:  return $True$  3: end if  4: if$rank(P,J)<rank(P,I)$then  5:  return $False$  6: end if  7: return$Crowding\_distance\left(P,I\right)>Crowding\_distance\left(P,J\right)$

The main reason ENORA and NSGA-II behave differently is as follows. NSGA-II never selects the individual dominated by the other in the binary tournament, while, in ENORA, the individual dominated by the other may be the winner of the tournament. Figure 1 shows this behavior graphically. For example, if individuals B and C are selected for a binary tournament with NSGA-II, individual B beats C because B dominates C. Conversely, individual C beats B with ENORA because individual C has a better rank in his slot than individual B. In this way, ENORA allows the individuals in each slot to evolve towards the Pareto front encouraging diversity. Even though in ENORA the individuals of each slot may not be the best of the total individuals, this approach generates a better hypervolume than that of NSGA-II throughout the evolution process.

ENORA is our MOEA, on which we are intensively working over the last decade. We have applied ENORA to constrained real-parameter optimization [17], fuzzy optimization [37], fuzzy classification [18], feature selection for classification [19] and feature selection for regression [34]. In this paper, we apply it to rule-based classification. NSGA-II algorithm was designed by Deb et al. and has been proved to be a very powerful and fast algorithm in multi-objective optimization contexts of all kinds. Most researchers in multi-objective evolutionary computation use NSGA-II as a baseline to compare the performance of their own algorithms. Although NSGA-II was developed in 2002 and remains a state-of-the-art algorithm, it is still a challenge to improve on it. There is a recently updated improved version for many-objective optimization problems called NSGA-III [38].

Algorithm 4 Crowding_distance function.

Require:P {Population} Require: P {Population} Require: I {Individual} Require: l {Number of objectives}  1: for$j=1$ to l do  2:  ${\displaystyle f_j^{max}\leftarrow \underset{I\in P}{max}\{f_j^I\}}$  3:  ${\displaystyle f_j^{min}\leftarrow \underset{I\in P}{min}\{f_j^I\}}$  4:  $f_j^{su{p}_j^I}\leftarrow$ value of the jth objective for the individual higher adjacent in the jth objective to the individual I  5:  $f_j^{in{f}_j^I}\leftarrow$ value of the jth objective for the individual lower adjacent in the jth objective to the individual I  6: end for  7: for$j=1$ to l do  8:  if $f_j^I=f_j^{max}$ or $f_j^I=f_j^{min}$ then  9:   return ∞ 10:  end if 11: end for 12: $CD\leftarrow 0.0$ 13: for$j=1$ to l do 14:  $CD\leftarrow CD+\frac{{\displaystyle f_j^{su{p}_j^I}-f_j^{in{f}_j^I}}}{{\displaystyle f_j^{max}-f_j^{min}}}$ 15: end for 16: return$CD$

2.3. PART

PART (Partial DT Method [39]) is a widely used rule learning algorithm that was developed at the University of Waikato in New Zealand [40]. Experiments show that it is a very efficient algorithm in terms of both computational performance and results. PART combines the divide-and-conquer strategy typical of decision tree learning with the separate-and-conquer strategy [41] typical of rule learning, as follows. A decision tree is first constructed (using C4.5 algorithm [42]), and the leaf with the highest coverage is converted into a rule. Then, the set of instances that are covered by that rule are discarded, and the process starts over. The result is an ordered set of rules, completed by a default rule that applies to instances that do not meet any previous rule.

2.4. JRip

JRip is a fast and optimized implementation in Weka of the famous RIPPER (Repeated Incremental Pruning to Produce Error Reduction) algorithm [43]. RIPPER was proposed in [44] as a more efficient version of the incrementally reduced error pruning (IREP) rule learner developed in [45]. IREP and RIPPER work in a similar manner. They begin with a default rule and, using a training dataset, attempt to learn rules that predict exceptions to the default. Each rule learned is a conjunction of propositional literals. Each literal corresponds to a split of the data based on the value of a single feature. This family of algorithms, similar to decision trees, has the advantage of being easy to interpret, and experiments show that JRip is particularly efficient in large datasets. RIPPER and IREP use a strategy based on the separate-and-conquer method to generate an ordered set of rules that are extracted directly from the dataset. The classes are examined one by one, prioritizing those that have more elements. These algorithms are based on four basic steps (growing, pruning, optimizing and selecting) applied repetitively to each class until a stopping condition is met [44]. These steps can be summarized as follows. In the growing phase, rules are created taking into account an increasing number of predictors until the stopping criterion is satisfied (in the Weka implementation, the procedure selects the condition with the highest information gain). In the pruning phase redundancy is eliminated and long rules are reduced. In the optimization phase, the rules generated in the previous steps are improved (if possible) by adding new attributes or by adding new rules. Finally, in the selection phase, the best rules are selected and the others discarded.

2.5. OneR

OneR (One Rule) is a very simple, while reasonably accurate, classifier based on a frequency table. First, OneR generates a set of rules for each attribute of the dataset, and, then, it selects only one rule from that set—the one with the lowest error rate [46]. The set of rules is created using a frequency table constructed for each predictor of the class, and numerical classes are converted into categorical values.

2.6. ZeroR

Finally, ZeroR (Zero Rules [40]) is a classifier learner that does not create any rules and uses no attributes. ZeroR simply creates the class classification table by selecting the most frequent value. Such a classifier is obviously the simplest possible one, and its capabilities are limited to the prediction of the majority class. In the literature, it is not used for practical classifications tasks, but as a generic reference to measure the performance of other classifiers.

3. Multi-Objective Optimization for Categorical Rule-Based Classification

In this section, we propose a general schema for an RBC specifically designed for categorical data. Then, we propose and describe a multi-objective optimization solution to obtain optimal categorical RBCs.

3.1. Rule-Based Classification for Categorical Data

Let $\Gamma$ be a classifier composed by M rules, where each rule $R_i^{\Gamma }$, $i=1,\dots ,M$, has the following structure:

$$\begin{array}{ccccccccc}{R}_i^{\Gamma }:\hfill & IF\hfill & x_1=b_{i1}^{\Gamma }\hfill & AND\hfill & ,\dots ,\hfill & AND\hfill & x_p=b_{ip}^{\Gamma }\hfill & THEN\hfill & y=c_i^{\Gamma }\hfill \end{array}$$

(2)

where for $j=1,\dots ,p$ the attribute $b_{ij}^{\Gamma }$ (called antecedent) takes values in a set $\{1,\dots ,v_j\}$ ($v_j>1$), and $c_i^{\Gamma }$ (called consequent) takes values in $\{1,\dots ,w\}$ ($w>1$). Now, let $\mathbf{x}=\{x_1,\dots ,x_p\}$ be an observed example, with $x_j\in \{1,\dots ,v_j\}$, for each $j=1,\dots ,p$. We propose maximum matching as reasoning method, where the compatibility degree of the rule $R_i^{\Gamma }$ for the example $\mathbf{x}$ (denoted by ${\phi }_i^{\Gamma }\left(\mathbf{x}\right)$) is calculated as the number of attributes whose value coincides with that of the corresponding antecedent in $R_i^{\Gamma }$, that is

$${\displaystyle {\phi }_i^{\Gamma }\left(\mathbf{x}\right)=\sum _{j=1}^p{\mu }_{ij}^{\Gamma }\left(\mathbf{x}\right)}$$

where:

$${\mu }_{ij}^{\Gamma }\left(\mathbf{x}\right)=\left\{\begin{array}{cc}1\hfill & if{x}_j=b_{ij}^{\Gamma }\hfill \\ 0\hfill & if{x}_j\ne b_{ij}^{\Gamma }\hfill \end{array}\right.$$

The association degree for the example $\mathbf{x}$ with a class $c\in \{1,\dots ,w\}$ is computed by adding the compatibility degrees for the example $\mathbf{x}$ of each rule $R_i^{\Gamma }$ whose consequent $c_i^{\Gamma }$ is equal to class c, that is:

$${\displaystyle {\lambda }_c^{\Gamma }\left(\mathbf{x}\right)=\sum _{i=1}^M{\eta }_{ic}^{\Gamma }\left(\mathbf{x}\right)}$$

where:

$${\eta }_{ic}^{\Gamma }\left(\mathbf{x}\right)=\left\{\begin{array}{cc}{\phi }_i^{\Gamma }\left(\mathbf{x}\right)\hfill & ifc=c_i^{\Gamma }\hfill \\ 0\hfill & ifc\ne c_i^{\Gamma }\hfill \end{array}\right.$$

Therefore, the classification (or output) of the classifier $\Gamma$ for the example $\mathbf{x}$ corresponds to the class whose association degree is maximum, that is:

$${\displaystyle f^{\Gamma }\left(\mathbf{x}\right)={arg}_c\underset{c=1}{\overset{w}{max}}{\lambda }_c^{\Gamma }\left(\mathbf{x}\right)}$$

3.2. A Multi-Objective Optimization Solution

Let $\mathcal{D}$ be a dataset of K instances with p categorical input attributes, $p>0$, and a categorical output attribute. Each input attribute j can take a category $x_j\in \left\{1,\dots ,v_j\right\}$, $v_j>1$, $j=1,\dots ,p$, and the output attribute can take a class $c\in \left\{1,\dots ,w\right\}$, $w>1$. The problem of finding an optimal classifier $\Gamma$, as described in the previous section, can be formulated as an instance of the multi-objective constrained problem in Equation (1) with two objectives and two constraints:

$$\begin{array}{cc}Max./Min.\hfill & {\mathcal{F}}_{\mathcal{D}}(\Gamma )\hfill \\ Min.\hfill & \mathcal{NR}(\Gamma )\hfill \\ subjectto:\hfill & \mathcal{NR}(\Gamma )\ge w\hfill \\ & \mathcal{NR}(\Gamma )\le M_{max}\hfill \end{array}$$

(3)

In the problem (Equation (3)), the function ${\mathcal{F}}_{\mathcal{D}}(\Gamma )$ is a performance measure of the classifier $\Gamma$ over the dataset $\mathcal{D}$, the function $\mathcal{NR}(\Gamma )$ is the number of rules of the classifier $\Gamma$, and the constraints $\mathcal{NR}(\Gamma )\ge w$ and $\mathcal{NR}(\Gamma )\le M_{max}$ limit the number of rules of the classifier $\Gamma$ to the interval $[w,M_{max}]$, where w is the number of classes of the output attribute and $M_{max}$ is given by a user. Objectives ${\mathcal{F}}_{\mathcal{D}}(\Gamma )$ and $\mathcal{NR}(\Gamma )$ are in conflict. The fewer rules the classifier has, the fewer instances it can cover, that is, if the classifier is simpler it will have less capacity for prediction. There is, therefore, an intrinsic conflict between problem objectives (e.g., maximize accuracy and minimize model complexity) which cannot be easily aggregated to a single objective. Both objectives are typically optimized simultaneously in many other classification systems, such as neural networks or decision trees [47,48]. Figure 2 shows the Pareto front of a dummy binary classification problem described as in Equation (3), with $M_{max}=6$ rules, where ${\mathcal{F}}_{\mathcal{D}}(\Gamma )$ is maximized. This front is composed of three non-dominated solutions (three possible classifiers) with two, three and four rules, respectively. The solutions with five and six rules are dominated (both by the solution with four rules).

Both ENORA and NSGA-II have been adapted to solve the problem described in Equation (3) with variable-length representation based on a Pittsburgh approach, uniform random initialization, binary tournament selection, handling constraints, ranking based on non-domination level with crowding distance, and self-adaptive variation operators. Self-adaptive variation operators work on different levels of the classifier: rule crossover, rule incremental crossover, rule incremental mutation, and integer mutation.

3.2.1. Representation

We use a variable-length representation based on a Pittsburgh approach [49], where each individual I of a population contains a variable number of rules $M_I$, and each rule $R_i^I$, $i=1,\dots ,$ is codified in the following components:

• Integer values associated to the antecedents $b_{ij}^I\in \{1,\dots ,v_j\}$, for $i=1,\dots ,M_I$ and $j=1,\dots ,p$.
• Integer values associated to the consequent $c_i^I\in \{1,\dots ,w\}$, for $i=1,\dots ,M_I$.

Additionally, to carry out self-adaptive crossing and mutation, each individual has two discrete parameters $d_I\in \{0,\dots ,\delta \}$ and $e_I\in \{0,\dots ,ϵ\}$ associated with crossing and mutation, where $\delta \ge 0$ is the number of crossing operators and $\epsilon \ge 0$ is the number of mutation operators. Values $d_I$ and $e_I$ for self-adaptive variation are randomly generated from $\{0,\delta \}$ and $\{0,ϵ\}$, respectively.

Table 1. Chromosome coding for an individual I.

Codification for Rule Set					Codification for Adaptive Crossing and Mutation
Antecedents				Consequent	Associated Crossing	Associated Mutation
$b_{11}^I$	$b_{21}^I$	…	$b_{q1}^I$	$c_1^I$
⋮	⋮	⋮	⋮	⋮	$d_I$	$e_I$
$b_{1M_I}^I$	$b_{2M_I}^I$	…	$b_{q{M}_I}^I$	$c_{M_I}^I$

summarizes the representation of an individual.

3.2.2. Constraint Handling

The constraints $\mathcal{NR}(\Gamma )\ge w$ and $\mathcal{NR}(\Gamma )\le M_{max}$ are satisfied by means of specialized initialization and variation operators, which always generate individuals with a number of rules between w and $M_{max}$.

3.2.3. Initial Population

The initial population (Algorithm 5) is randomly generated with the following conditions:

• Individuals are uniformly distributed with respect to the number of rules with values between w and $M_{max}$, and with an additional constraint that specifies that there must be at least one individual for each number of rules (Steps 4–8). This ensures an adequate initial diversity in the search space in terms of the second objective of the optimization model.
• All individuals contain at least one rule for any output class between 1 and w (Steps 16–20).

Algorithm 5 Initialize population.

Require:$p>0$ {Number of categorical input attributes} Require: $v_1,\dots ,v_p$, $v_j>1$, $j=1,\dots ,p$ {Number of categories for the input attributes} Require: $w>1$, {Number of classes for the output attribute} Require: $\delta >0$ {Number of crossing operators} Require: $ϵ>0$ {Number of mutation operators} Require: $M_{max}\ge w$ {Maximum number of rules} Require: $N>1$ {Number of individuals in the population}  1: $P\leftarrow \varnothing$  2: for$k=1$ to N do  3:  $I\leftarrow$ new Individual  4:  if $k\le M_{max}-w+1$ then  5:   $M_I\leftarrow k+w-1$  6:  else  7:   $M_I\leftarrow$ Int Random(w,$M_{max}$)  8:  end if  9:  {Random rule $R_i^I$} 10:  for $i=1$ to $M_I$ do 11:   {Random integer values associated with the antecedents} 12:   for $j=1$ to p do 13:    $b_{ij}^I\leftarrow$Random(1,$v_j$) 14:   end for 15:   {Random integer value associated with the consequent} 16:   if $i<w$ then 17:    $c_i^I=j$ 18:   else 19:    $c_i^I\leftarrow$Random(1,w) 20:   end if 21:  end for 22:  {Random integer values for adaptive variation} 23:  $d_I\leftarrow$Random(0,$\delta$) 24:  $e_I\leftarrow$Random(0,$ϵ$) 25:  $P\leftarrow P\cup I$ 26: end for 27: returnP

3.2.4. Fitness Functions

Since the optimization model encompasses two objectives, each individual must be evaluated with two fitness functions, which correspond to the objective functions ${\mathcal{F}}_{\mathcal{D}}(\Gamma )$ and $\mathcal{NR}(\Gamma )$ of the problem (Equation (3)). The selection of the best individuals is done using the Pareto concept in a binary tournament.

3.2.5. Variation Operators

We use self-adaptive crossover and mutation, which means that the selection of the operators is made by means of an adaptive technique. As we have explained (cf. Section 3.2.1), each individual I has two integer parameters $d_I\in \left\{0,\dots ,\delta \right\}$ and $e_I\in \left\{0,\dots ,ϵ\right\}$ to indicate which crossover or mutation is carried out. In our case, $\delta =2$ and $ϵ=2$ are two crossover operators and two mutation operators, so that $d_I,e_I\in \{0,1,2\}$. Note that value 0 indicates that no crossover or no mutation is performed. Self-adaptive variation (Algorithm 6) generates two children from two parents by self-adaptive crossover (Algorithm 7) and self-adaptive mutation (Algorithm 8). Self-adaptive crossover of individuals $I,J$ and self-adaptive mutation of individual I are similar to each other. First, with a probability $p_v$, the values $d_I$ and $e_I$ are replaced by a random value. Additionally, in the case of crossover, the value $d_J$ is replaced by $d_I$. Then, the crossover indicated by $d_I$ or the mutation indicated by $e_I$ is performed. In summary, if an individual comes from a given crossover or a given mutation, that specific crossover and mutation are preserved to their offspring with probability $p_v$, so the value of $p_v$ must be small enough to ensure a controlled evolution (in our case, we use $p_v=0.1$). Although the probability of the crossover and mutation is not explicitly represented, it can be computed as the ratio of the individuals for which crossover and mutation values are set to 1. As the population evolves, individuals with more successful types of crossover and mutation will be more common, so that the probability of selecting the more successful crossover and mutation types will increase. Using self-adaptive crossover and mutation operators helps to realize the goals of maintaining diversity in the population and sustaining the convergence capacity of the evolutionary algorithm, also eliminating the need of setting an a priori operator probability to each operator. In other approaches (e.g., [50]), the probabilities of crossover and mutation vary depending on the fitness value of the solutions.

Both ENORA and NSGA-II have been implemented with two crossover operators, rule crossover (Algorithm 9) and rule incremental crossover (Algorithm 10), and two mutation operators: rule incremental mutation (Algorithm 11) and integer mutation (Algorithm 12). Rule crossover randomly exchanges two rules selected from the parents, and rule incremental crossover adds to each parent a rule randomly selected from the other parent if its number of rules is less than the maximum number of rules. On the other hand, rule incremental mutation adds a new rule to the individual if the number of rules of the individual is less than the maximum number of rules, while integer mutation carries out a uniform mutation of a random antecedent belonging to a randomly selected rule.

Algorithm 6 Variation.

Require:$Parent1$, $Parent2$ {Individuals for variation}  1: $Child1\leftarrow Parent1$  2: $Child1\leftarrow Parent2$  3: Self-adaptive crossover $Child1$, $Child2$  4: Self-adaptive mutation $Child1$  5: Self-adaptive mutation $Child2$  6: return$Child1,Child2$

Algorithm 7 Self-adaptive crossover.

Require:I, J {Individuals for crossing} Require: $p_v$ ($0<p_v<1$) {Probability of variation} Require: $\delta >0$ {Number of different crossover operators}  1: if a random Bernoulli variable with probability $p_v$ takes the value 1 then  2:  $d_I\leftarrow$Random(0,$\delta$)  3: end if  4: $d_J\leftarrow d_I$  5: Carry out the type of crossover specified by $d_I$: {0: No cross} {1: Rule crossover} {2: Rule incremental crossover}

Algorithm 8 Self-adaptive mutation.

Require:I {Individual for mutation} Require: $p_v$ ($0<p_v<1$) {Probability of variation} Require: $ϵ>0$ {Number of different mutation operators}  1: if a random Bernoulli variable with probability $p_v$ takes the value 1 then  2:  $e_I\leftarrow$Random(0,$ϵ$)  3: end if  4: Carry out the type of mutation specified by $e_I$: {0: No mutation} {1: Rule incremental mutation} {2: Integer mutation}

Algorithm 9 Rule crossover.

Require:I, J {Individuals for crossing}  1: $i\leftarrow$Random(1,$M_I$)  2: $j\leftarrow$Random(1,$M_J$)  3: Exchange rules $R_i^I$ and $R_j^J$

Algorithm 10 Rule incremental crossover.

Require:I, J {Individuals for crossing} Require: $M_{max}$ {Maximum number of rules}  1: if$M_I<M_{max}$then  2:  $j\leftarrow$Random(1,$M_J$)  3:  Add $R_j^J$ to individual I  4: end if  5: if$M_J<M_{max}$then  6:  $i\leftarrow$Random(1,$M_I$)  7:  Add $R_i^I$ to individual J  8: end if

Algorithm 11 Rule incremental mutation.

Require:I {Individual for mutation} Require: $M_{max}$ {Maximum number of rules}  1: if$M_I<M_{max}$then  2:  Add a new random rule to I  3: end if

Algorithm 12 Integer mutation.

Require:I {Individual for mutation} Require: $p>0$ {Number of categorical input attributes} Require: $v_1,\dots ,v_p$,  $v_j>1$,  $j=1,\dots ,p$ {Number of categories for the input attributes}  1: $i\leftarrow$Random(1,$M_I$)  2: $j\leftarrow$Random(1,p)  3: $b_{ij}^I\leftarrow$Random(1,$v_j$)

4. Experiment and Results

To ensure the reproducibility of the experiments, we have used publicly available datasets. In particular, we have designed two sets of experiments, one using the Breast Cancer [51] dataset, and the other using the Monk’s Problem 2 [52] dataset.

4.1. The Breast Cancer Dataset

Breast Cancer encompasses 286 instances. Each instance corresponds to a patient who suffered from breast cancer and uses nine attributes to describe each patient. The class to be predicted is binary and represents whether the patient has suffered a recurring cancer event. In this dataset, 85 instances are positive and 201 are negative.

Table 2. Attribute description of the Breast Cancer dataset.

#	Attribute Name	Type	Possible Values
1	age	categorical	10–19, 20–29, 30–39, 40–49, 50–59, 60–69, 70–79, 80–89, 90–99.
2	menopause	categorical	lt40, ge40, premeno
3	tumour-size	categorical	0–4, 5–9, 10–14, 15–19, 20–24, 25–29, 30–34, 35–39, 40–44, 45–49, 50–54, 55–59
4	inv-nodes	categorical	0–2, 3–5, 6–8, 9–11, 12–14, 15–17, 18–20, 21–23, 24–26, 27–29, 30–32, 33–35, 36–39
5	node-caps	categorical	yes, no
6	deg-malign	categorical	1, 2, 3
7	breast	categorical	left, right
8	breast-quad	categorical	left-up, left-low, right-up, right-low, central
9	irradiat	categorical	yes, no
10	class	categorical	no-recurrence-events, recurrence-events

summarizes the attributes of the dataset. Among all instances, nine present some missing values; in the pre-processing phase, these have been replaced by the mode of the corresponding attribute.

4.2. The Monk’s Problem 2 Dataset

In July 1991, the monks of Corsendonk Priory attended a summer course that was being held in their priory, namely the 2nd European Summer School on Machine Learning. After a week, the monks could not yet clearly identify the best ML algorithms, or which algorithms to avoid in which cases. For this reason, they decided to create the three so-called Monk’s problems, and used them to determine which ML algorithms were the best. These problems, rather simple and completely artificial, became later famous (because of their peculiar origin), and have been used as a comparison for many algorithms on several occasions. In particular, in [53], they have been used to test the performance of state-of-the-art (at that time) learning algorithms such as AQ17-DCI, AQ17-HCI, AQ17-FCLS, AQ14-NT, AQ15-GA, Assistant Professional, mFOIL, ID5R, IDL, ID5R-hat, TDIDT, ID3, AQR, CN2, WEB CLASS, ECOBWEB, PRISM, Backpropagation, and Cascade Correlation. For our research, we have used the Monk’s Problem 2, which contains six categorical input attributes and a binary output attribute, summarized in

Table 3. Attribute description of the MONK’s Problem 2 dataset.

#	Atttribute Name	Type	Possible Values
1	head_shape	categorical	round, square, octagon
2	body_shape	categorical	round, square, octagon
3	is_smiling	categorical	yes, no
4	holding	categorical	sword, balloon, flag
5	jacket_color	categorical	red, yellow, green, blue
6	has_tie	categorical	yes, no
7	class	categorical	yes, no

. The target concept associated with the Monk’s Problem 2 is the binary outcome of the logical formula:

Exactly two of:
{heap_shape= round, body_shape=round, is_smiling=yes, holding=sword, jacket_color=red,
has_tie=yes}

In this dataset, the original training and testing sets were merged to allow other sampling procedures. The set contains a total of 601 instances, and no missing values.

4.3. Optimization Models

We have conducted different experiments with different optimization models to calculate the overall performance of our proposed technique and to see the effect of optimizing different objectives for the same problem. First, we have designed a multi-objective constrained optimization model based on the accuracy:

$$\begin{array}{cc}Max.\hfill & {\mathcal{ACC}}_{\mathcal{D}}(\Gamma )\hfill \\ Min.\hfill & \mathcal{NR}(\Gamma )\hfill \\ subjectto:\hfill & \mathcal{NR}(\Gamma )\ge w\hfill \\ & \mathcal{NR}(\Gamma )\le M_{max}\hfill \end{array}$$

(4)

where ${\mathcal{ACC}}_{\mathcal{D}}(\Gamma )$ is the proportion of correctly classified instances (both true positives and true negatives) among the total number of instances [54] obtained with the classifier $\Gamma$ for the dataset $\mathcal{D}$. ${\mathcal{ACC}}_{\mathcal{D}}(\Gamma )$ is defined as:

$${\displaystyle {\mathcal{ACC}}_{\mathcal{D}}(\Gamma )=\frac{1}{K}\sum _{i=1}^K{T}_{\mathcal{D}}(\Gamma ,i)}$$

where K is the number of instances of the dataset $\mathcal{D}$, and $T_{\mathcal{D}}(\Gamma ,i)$ is the result of the classification of the instance i in $\mathcal{D}$ with the classifier $\Gamma$, that is:

$$T_{\mathcal{D}}(\Gamma ,i)=\left\{\begin{array}{cc}1\hfill & if{\widehat{c}}_i^{\Gamma }=c_{\mathcal{D}}^i\hfill \\ 0\hfill & if{\widehat{c}}_i^{\Gamma }\ne c_{\mathcal{D}}^i\hfill \end{array}\right.$$

where ${\widehat{c}}_i^{\Gamma }$ is the predicted value of the ith instance in $\Gamma$, and $c_{\mathcal{D}}^i$ is the corresponding true value in $\mathcal{D}$. Our second optimization model is based on the area under the ROC curve:

$$\begin{array}{cc}Max.\hfill & {\mathcal{AUC}}_{\mathcal{D}}(\Gamma )\hfill \\ Min.\hfill & \mathcal{NR}(\Gamma )\hfill \\ subjectto:\hfill & \mathcal{NR}(\Gamma )\ge w\hfill \\ & \mathcal{NR}(\Gamma )\le M_{max}\hfill \end{array}$$

(5)

where ${\mathcal{AUC}}_{\mathcal{D}}(\Gamma )$ is the area under the ROC curve obtained with the classifier $\Gamma$ with the dataset $\mathcal{D}$. The ROC (Receiver Operating Characteristic) curve [55] is a graphical representation of the sensitivity versus the specificity index for a classifier varying the discrimination threshold value. Such a curve can be used to generate statistics that summarize the performance of a classifier, and it has been shown in [54] to be a simple, yet complete, empirical description of the decision threshold effect, indicating all possible combinations of the relative frequencies of the various kinds of correct and incorrect decisions. The area under the ROC curve can be computed as follows [56]:

$${\mathcal{AUC}}_{\mathcal{D}}(\Gamma )={\int }_0^1{S}_{\mathcal{D}}(\Gamma ,E_{\mathcal{D}}^{-1}(\Gamma ,v))dv$$

where $S_{\mathcal{D}}(\Gamma ,t)$ (sensitivity) is the proportion of positive instances classified as positive by the classifier $\Gamma$ in $\mathcal{D}$, $1-E_{\mathcal{D}}(\Gamma ,t)$ (specificity) is the proportion of negative instances classified as negative by $\Gamma$ in $\mathcal{D}$, and t is the discrimination threshold. Finally, our third constrained optimization model is based on the root mean square error (RMSE):

$$\begin{array}{cc}Max./Min.\hfill & {\mathcal{RMSE}}_{\mathcal{D}}(\Gamma )\hfill \\ Min.\hfill & \mathcal{NR}(\Gamma )\hfill \\ subjectto:\hfill & \mathcal{NR}(\Gamma )\ge w\hfill \\ & \mathcal{NR}(\Gamma )\le M_{max}\hfill \end{array}$$

(6)

where ${\mathcal{RMSE}}_{\mathcal{D}}(\Gamma )$ is defined as the square root of the mean square error obtained with a classifier $\Gamma$ in the dataset $\mathcal{D}$:

$${\mathcal{RMSE}}_{\mathcal{D}}(\Gamma )=\frac{1}{K}\sqrt{{\displaystyle \sum _{i=1}^K{({\widehat{c}}_i^{\Gamma }-c_{\mathcal{D}}^i)}^2}}$$

where ${\widehat{c}}_i^{\Gamma }$ is the predicted value of the ith instance for the classifier $\Gamma$, and $c_{\mathcal{D}}^i$ is the corresponding output value in the database $\mathcal{D}$. Accuracy, area under the ROC curve, and root mean square error are all well-accepted measures used to evaluate the performance of a classifier. Therefore, it is natural to use such measures as fitting functions. In this way, we can establish which one behaves better in the optimization phase, and we can compare the results with those in the literature.

4.4. Choosing the Best Pareto Front

To compare the performance of ENORA and NSGA-II as metaheuristics in this particular optimization task, we use the hypervolume metric [57,58]. The hypervolume measures, simultaneously, the diversity and the optimality of the non-dominated solutions. The main advantage of using hypervolume against other standard measures, such as the error ratio, the generational distance, the maximum Pareto-optimal front error, the spread, the maximum spread, or the chi-square-like deviation, is that it can be computed without an optimal population, which is not always known [15]. The hypervolume is defined as the volume of the search space dominated by a population P, and is formulated as:

$$HV\left(P\right)=\bigcup _{i=1}^{\left|Q\right|}{v}_i$$

(7)

where $Q\subseteq P$ is the set of non-dominated individuals of P, and $v_i$ is the volume of the individual i. Subsequently, the hypervolume ratio (HVR) is defined as the ratio of the volume of the non-dominated search space over the volume of the entire search space, and is formulated as follows:

$$HVR\left(P\right)=1-\frac{H\left(P\right)}{VS}$$

(8)

where $VS$ is the volume of the search space. Computing HVR requires reference points that identify the maximum and minimum values for each objective. For RBC optimization, as proposed in this work, the following minimum (${\mathcal{F}}_{\mathcal{D}}^{lower}$, ${\mathcal{NR}}^{lower}$) and maximum (${\mathcal{F}}_{\mathcal{D}}^{upper}$, ${\mathcal{NR}}^{upper}$) points, for each objective, are set in the multi-objective optimization models in Equations (4)–(6):

$${\mathcal{F}}_{\mathcal{D}}^{lower}=0,{\mathcal{F}}_{\mathcal{D}}^{upper}=1,{\mathcal{NR}}^{lower}=w,{\mathcal{NR}}^{upper}=M_{max}$$

A first single execution of all six models (three driven by ENORA, and three driven by NSGA-II), over both datasets, has been designed for the purpose of showing the aspect of the final Pareto front, and compare the hypervolume ratio of the models. The results of this single execution, with population size equal to 50 and 20,000 generations (1,000,000 evaluations in total), are shown in Figure 3 and Figure 4 (by default, $M_{max}$ is set to 10, to which we add 2, because both datasets have a binary class). Regarding the configuration of the number of generations and the size of the population, our criterion has been established as follows: once the number of evaluations is set to 1,000,000, we can decide to use a population size of 100 individuals and 10,000 generations, or to use a population size of 50 individuals and 20,000 generations. The first configuration (100 × 10,000) allows a greater diversity with respect to the number of rules of the classifiers, while the second one (50 × 20,000) allows a better adjustment of the classifier parameters and therefore, a greater precision. Given the fact that the maximum number of rules of the classifiers is not greater than 12, we think that 50 individuals are sufficient to represent four classifiers on average for each number of rules (4 × 12 = 48∼50). Thus, we prefer the second configuration ($50\times$ 20,000) because having more generations increases the chances of building classifiers with a higher precision.

Experiments were executed in a computer x64-based PC with one processor Intel64 Family 6 Model 60 Stepping 3 GenuineIntel 3201 Mhz, RAM 8131 MB.

Table 4. Run times of ENORA and NSGA-II for Breast Cancer and Monk’s Problem 2 datasets.

Method	Breast Cancer	Monk’s Problem 2
ENORA-ACC	244.92 s.	428.14 s.
ENORA-AUC	294.75 s.	553.11 s.
ENORA-RMSE	243.30 s.	414.42 s.
NSGA-II-ACC	127.13 s.	260.83 s.
NSGA-II-AUC	197.07 s.	424.83 s.
NSGA-II-RMSE	134.87 s.	278.19 s.

shows the run time for each method over both datasets. Note that, although ENORA has less algorithmic complexity than NSGA-II, it has taken longer in experiments than NSGA-II. This is because the evaluation time of individuals in ENORA is higher than that of NSGA-II since ENORA has more diversity than NSGA-II, and therefore ENORA evaluates classifiers with more rules than NSGA-II.

From these results, we can deduce that, first, ENORA maintains a higher diversity of the population, and achieves a better hypervolume ratio with respect to NSGA-II, and, second, using accuracy as the first objective generates better fronts than using the area under the ROC curve, which, in turn, performs better than using the root mean square error.

4.5. Comparing Our Method with Other Classifier Learning Systems (Full Training Mode)

To perform an initial comparison between the performance of the classifiers obtained with the proposed method and the ones obtained with classical methods (PART, JRip, OneR and ZeroR), we have executed again the six models in full training mode.

The parameters have been configured as in the previous experiment (population size equal to 50 and 20,000 generations), excepting the $M_{max}$ parameter that was set to 2 for the Breast Cancer dataset (this case), while, for the Monk’s Problem 2, it was set to 9. Observe that, since $M_{min}=2$ in both cases, executing the optimization models using $M_{max}=2$ leads to a single objective search for the Breast Cancer dataset. In fact, after the preliminary experiments were run, it turned out that the classical classifier learning systems tend to return very small, although not very precise, set of rules on Breast Cancer, and that justifies our choice. On the other hand, executing the classical rule learners on Monk’s Problem 2 returns more diverse sets of rules, which justifies choosing a higher $M_{max}$ in that case. To decide, a posteriori, which individual is chosen from the final front, we have used the default algorithm: the individual with the best value on the first objective is returned. In the case of Monk’s Problem 2, that individual has seven rules. The comparison is shown in

Table 5. Comparison of the performance of the learning models in full training mode—Breast Cancer dataset.

Learning Model	Number of Rules	Percent Correct	TP Rate	FP Rate	Precision	Recall	F-Measure	MCC	ROC Area	PRC Area	RMSE
ENORA-ACC	2	79.02	0.790	0.449	0.796	0.790	0.762	0.455	0.671	0.697	0.458
ENORA-AUC	2	75.87	0.759	0.374	0.751	0.759	0.754	0.402	0.693	0.696	0.491
ENORA-RMSE	2	77.62	0.776	0.475	0.778	0.776	0.744	0.410	0.651	0.680	0.473
NSGA-II-ACC	2	77.97	0.780	0.501	0.805	0.780	0.738	0.429	0.640	0.679	0.469
NSGA-II-AUC	2	75.52	0.755	0.368	0.749	0.755	0.752	0.399	0.693	0.696	0.495
NSGA-II-RMSE	2	79.37	0.794	0.447	0.803	0.794	0.765	0.467	0.673	0.700	0.454
PART	15	78.32	0.783	0.397	0.773	0.783	0.769	0.442	0.777	0.793	0.398
JRip	3	76.92	0.769	0.471	0.762	0.769	0.740	0.389	0.650	0.680	0.421
OneR	1	72.72	0.727	0.563	0.703	0.727	0.680	0.241	0.582	0.629	0.522
ZeroR	-	70.27	0.703	0.703	0.494	0.703	0.580	0.000	0.500	0.582	0.457

and

Table 6. Comparison of the performance of the learning models in full training mode—Monk’s Problem 2 dataset.

Learning Model	Number of Rules	Percent Correct	TP Rate	FP Rate	Precision	Recall	F-Measure	MCC	ROC Area	PRC Area	RMSE
ENORA-ACC	7	75.87	0.759	0.370	0.753	0.759	0.745	0.436	0.695	0.680	0.491
ENORA-AUC	7	68.71	0.687	0.163	0.836	0.687	0.687	0.523	0.762	0.729	0.559
ENORA-RMSE	7	77.70	0.777	0.360	0.777	0.777	0.762	0.481	0.708	0.695	0.472
NSGA-II-ACC	7	68.38	0.684	0.588	0.704	0.684	0.597	0.203	0.548	0.580	0.562
NSGA-II-AUC	7	66.38	0.664	0.175	0.830	0.664	0.661	0.497	0.744	0.715	0.580
NSGA-II-RMSE	7	68.71	0.687	0.591	0.737	0.687	0.595	0.226	0.548	0.583	0.559
PART	47	94.01	0.940	0.087	0.940	0.940	0.940	0.866	0.980	0.979	0.218
JRip	1	65.72	0.657	0.657	0.432	0.657	0.521	0.000	0.500	0.549	0.475
OneR	1	65.72	0.657	0.657	0.432	0.657	0.521	0.000	0.500	0.549	0.585
ZeroR	-	65.72	0.657	0.657	0.432	0.657	0.521	0.000	0.500	0.549	0.475

, which show, for each classifier, the following information: number of rules, percent correct, true positive rate, false positive rate, precision, recall, F-measure, Matthews correlation coefficient, area under the ROC curve, area under precision-recall curve, and root mean square error. As for the Breast Cancer dataset (observe that the best result emerged from the proposed method), in the optimization model driven by NSGA-II, with root mean square error as the first objective (see

Table 7. Rule-based classifier obtained with NSGA-II-RMSE for Breast Cancer dataset.

Rule	Antecedents							Consequent
$R_1$:	IF	age = 50–59	AND	inv-nodes = 0–2	AND	node-caps = no
	AND	deg-malig = 1	AND	breast = right	AND	breast-quad = left-low	THEN	class = no-recurrence-events
$R_2$:	IF	age = 60–69	AND	inv-nodes = 18–20	AND	node-caps = yes
	AND	deg-malig = 3	AND	breast = left	AND	breast-quad = right-up	THEN	class = recurrence-events

), only PART was able to achieve similar results, although slightly worse, but at the price of having 15 rules, making the system clearly not interpretable. In the case of the Monk’s Problem 2 dataset, PART returned a model with 47 rules, which is not interpretable by any standard, although it is very accurate. The best interpretable result is the one with seven rules returned by ENORA, driven by the root mean square error (see

Table 8. Rule-based classifier obtained with ENORA-RMSE for Monk’s Problem 2 dataset.

Rule	Antecedents							Consequent
$R_1$:	IF	head_shape = round	AND	body_shape = round	AND	is_smiling = no
	AND	holding = sword	AND	jacket_color = red	AND	has_tie = yes	THEN	class = yes
$R_2$:	IF	head_shape = octagon	AND	body_shape = round	AND	is_smiling = no
	AND	holding = sword	AND	jacket_color = red	AND	has_tie = no	THEN	class = yes
$R_3$:	IF	head_shape = round	AND	body_shape = round	AND	is_smiling = no
	AND	holding = sword	AND	jacket_color = yellow	AND	has_tie = yes	THEN	class = yes
$R_4$:	IF	head_shape = round	AND	body_shape = round	AND	is_smiling = no
	AND	holding = sword	AND	jacket_color = red	AND	has_tie = no	THEN	class = yes
$R_5$:	IF	head_shape = square	AND	body_shape = square	AND	is_smiling = yes
	AND	holding = flag	AND	jacket_color = yellow	AND	has_tie = no	THEN	class = no
$R_6$:	IF	head_shape = octagon	AND	body_shape = round	AND	is_smiling = yes
	AND	holding = balloon	AND	jacket_color = blue	AND	has_tie = no	THEN	class = no
$R_7$:	IF	head_shape = octagon	AND	body_shape = octagon	AND	is_smiling = yes
	AND	holding = sword	AND	jacket_color = green	AND	has_tie = no	THEN	class = no

). The experiments for classical learners have been conducted using the default parameters.

4.6. Comparing Our Method with Other Classifier Learning Systems (Cross-Validation and Train/Test Percentage Split Mode)

To test the capabilities of our methodology in a more significant way, we proceeded as follows. First, we designed a cross-validated experiment for the Breast Cancer dataset, in which we iterated three times a 10-fold cross-validation learning process [59] and considered the average value of the performance metrics percent correct, area under the ROC curve, and serialized model size of all results. Second, we designed a train/test percentage split experiment for the Monk’s Problem 2 dataset, in which we iterated ten times a 66% (training) versus 33% (testing) split and considered, again, the average result of the same metrics. Finally, we performed a statistical test over on results, to understand if they show any statistically significant difference. An execution of our methodology, and of standard classical learners, has been performed to obtain the models to be tested precisely under the same conditions of the experiment Section 4.5. It is worth observing that using two different types of evaluations allows us to make sure that our results are not influenced by the type of experiment. The results of the experiments are shown in

Table 9. Comparison of the performance of the learning models in 10-fold cross-validation mode (three repetitions)—Breast Cancer dataset.

Learning Model	Percent Correct	ROC Area	Serialized Model Size
ENORA-ACC	73.45	0.61	9554.80
ENORA-AUC	70.16	0.62	9554.63
ENORA-RMSE	72.39	0.60	9557.77
NSGA-II-ACC	72.50	0.60	9556.20
NSGA-II-AUC	70.03	0.61	9555.70
NSGA-II-RMSE	73.34	0.60	9558.60
PART	68.92	0.61	55,298.13
JRip	71.82	0.61	7664.07
OneR	67.15	0.55	1524.00
ZeroR	70.30	0.50	915.00

and

Table 10. Comparison of the performance of the learning models in split mode—Monk’s problem 2 dataset.

Learning Model	Percent Correct	ROC Area	Serialized Model Size
ENORA-ACC	76.69	0.70	9586.50
ENORA-AUC	72.82	0.79	9589.30
ENORA-RMSE	75.66	0.68	9585.30
NSGA-II-ACC	70.07	0.59	9590.60
NSGA-II-AUC	67.08	0.70	9619.70
NSGA-II-RMSE	67.63	0.54	9565.90
PART	73.51	0.79	73,115.90
JRip	64.05	0.50	5956.90
OneR	65.72	0.50	1313.00
ZeroR	65.72	0.50	888.00

.

The statistical tests aim to verify if there are significant differences among the means of each metric: percent correct, area under the ROC curve and serialized model size. We proceeded as follows. First, we checked normality and sphericity of each sample by means of the Shapiro–Wilk normality test. Then, if normality and sphericity conditions were met, we applied one way repeated measures ANOVA; otherwise, we applied the Friedman test. In the latter case, when statistically significant differences were detected, we applied the Nemenyi post-hoc test to locate where these differences were.

Table A1. Shapiro–Wilk normality test p-values for percent correct metric—Breast Cancer dataset.

Algorithm	p-Value	Null Hypothesis
ENORA-ACC	0.5316	Not Rejected
ENORA-AUC	0.3035	Not Rejected
ENORA-RMSE	0.7609	Not Rejected
NSGA-II-ACC	0.1734	Not Rejected
NSGA-II-AUC	0.3802	Not Rejected
NSGA-II-RMSE	0.6013	Not Rejected
PART	0.0711	Not Rejected
JRip	0.5477	Not Rejected
OneR	0.316	Not Rejected
ZeroR	3.818 × 10${}^{-06}$	Rejected

,

Table A2. Friedman p-value for percent correct metric—Breast Cancer dataset.

	p-Value	Null Hypothesis
Friedman	5.111 × 10${}^{-04}$	Rejected

,

Table A3. Nemenyi post-hoc procedure for percent correct metric—Breast Cancer dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART	JRip	OneR
ENORA-AUC	0.2597	-	-	-	-	-	-	-	-
ENORA-RMSE	0.9627	0.9627	-	-	-	-	-	-	-
NSGA-II-ACC	0.9981	0.8047	1.0000	-	-	-	-	-	-
NSGA-II-AUC	0.2951	1.0000	0.9735	0.8386	-	-	-	-	-
NSGA-II-RMSE	1.0000	0.2169	0.9436	0.9960	0.2486	-	-	-	-
PART	0.1790	1.0000	0.9186	0.6997	1.0000	0.1461	-	-	-
JRip	0.9909	0.8956	1.0000	1.0000	0.9186	0.9840	0.8164	-	-
OneR	0.0004	0.6414	0.0451	0.0108	0.5961	0.0002	0.7546	0.0212	-
ZeroR	0.2377	1.0000	0.9538	0.7803	1.0000	0.1973	1.0000	0.8783	0.6709

,

Table A4. Summary of statistically significant differences for percent correct metric—Breast Cancer dataset.

	ENORA-ACC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-RMSE	JRip
OneR	ENORA-ACC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-RMSE	JRip

,

Table A5. Shapiro–Wilk normality test p-values for area under the ROC curve metric—Breast Cancer dataset.

Algorithm	p-Value	Null Hypothesis
ENORA-ACC	0.6807	Not Rejected
ENORA-AUC	0.3171	Not Rejected
ENORA-RMSE	0.6125	Not Rejected
NSGA-II-ACC	0.0871	Not Rejected
NSGA-II-AUC	0.5478	Not Rejected
NSGA-II-RMSE	0.6008	Not Rejected
PART	0.6066	Not Rejected
JRip	0.2978	Not Rejected
OneR	0.4531	Not Rejected
ZeroR	0.0000	Rejected

,

Table A6. Friedman p-value for area under the ROC curve metric—Breast Cancer dataset.

	p-Value	Null Hypothesis
Friedman	8.232 × 10${}^{-10}$	Rejected

,

Table A7. Nemenyi post-hoc procedure for area under the ROC curve metric—Breast Cancer dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART	JRip	OneR
ENORA-AUC	1.0000	-	-	-	-	-	-	-	-
ENORA-RMSE	0.9972	0.9990	-	-	-	-	-	-	-
NSGA-II-ACC	0.9999	1.0000	1.0000	-	-	-	-	-	-
NSGA-II-AUC	1.0000	1.0000	1.0000	1.0000	-	-	-	-	-
NSGA-II-RMSE	0.9990	0.9997	1.0000	1.0000	1.0000	-	-	-	-
PART	0.9999	1.0000	1.0000	1.0000	1.0000	1.0000	-	-	-
JRip	1.0000	1.0000	0.9992	1.0000	1.0000	0.9998	1.0000	-	-
OneR	0.0041	0.0062	0.0790	0.0323	0.0281	0.0582	0.0345	0.0067	-
ZeroR	3.8 × 10${}^{-07}$	7.2 × 10${}^{-07}$	4.6 × 10${}^{-05}$	9.8 × 10${}^{-06}$	7.8 × 10${}^{-06}$	2.7 × 10${}^{-05}$	1.1 × 10${}^{-05}$	8.1 × 10${}^{-07}$	0.6854

,

Table A8. Summary of statistically significant differences for area under the ROC curve metric—Breast Cancer dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART	JRip
OneR	ENORA-ACC	ENORA-AUC	-	NSGA-II-ACC	NSGA-II-AUC	-	PART	JRip
ZeroR	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART	JRip

,

Table A9. Shapiro–Wilk normality test p-values for serialized model size metric—Breast Cancer dataset.

Algorithm	p-Value	Null Hypothesis
ENORA-ACC	5.042 × 10${}^{-05}$	Rejected
ENORA-AUC	2.997 × 10${}^{-07}$	Rejected
ENORA-RMSE	4.762 × 10${}^{-04}$	Rejected
NSGA-II-ACC	4.88 × 10${}^{-06}$	Rejected
NSGA-II-AUC	2.339 × 10${}^{-07}$	Rejected
NSGA-II-RMSE	2.708 × 10${}^{-06}$	Rejected
PART	0.3585	Not Rejected
JRip	9.086 × 10${}^{-03}$	Rejected
OneR	1.007 × 10${}^{-07}$	Rejected
ZeroR	0.0000	Rejected

,

Table A10. Friedman p-value for serialized model size metric—Breast Cancer dataset.

	p-Value	Null Hypothesis
Friedman	2.2 × 10${}^{-16}$	Rejected

,

Table A11. Nemenyi post-hoc procedure for serialized model size metric—Breast Cancer dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART	JRip	OneR
ENORA-AUC	0.9998	-	-	-	-	-	-	-	-
ENORA-RMSE	0.0053	0.0004	-	-	-	-	-	-	-
NSGA-II-ACC	0.3871	0.0942	0.8872	-	-	-	-	-	-
NSGA-II-AUC	0.8872	0.4894	0.3871	0.9988	-	-	-	-	-
NSGA-II-RMSE	4.1 × 10${}^{-05}$	1.3 × 10${}^{-06}$	0.9860	0.2169	0.0244	-	-	-	-
PART	4.7 × 10${}^{-09}$	5.6 × 10${}^{-11}$	0.1973	0.0013	3.3 × 10${}^{-05}$	0.8689	-	-	-
JRip	0.2712	0.6997	1.2 × 10${}^{-08}$	7.0 × 10${}^{-05}$	0.0025	6.3 × 10${}^{-12}$	6.9 × 10${}^{-14}$	-	-
OneR	0.0062	0.0546	1.5 × 10${}^{-12}$	5.5 × 10${}^{-08}$	5.5 × 10${}^{-06}$	8.3 × 10${}^{-14}$	8.3 × 10${}^{-14}$	0.9584	-
ZeroR	1.9 × 10${}^{-05}$	0.0004	7.3 × 10${}^{-14}$	8.6 × 10${}^{-12}$	2.3 × 10${}^{-09}$	8.5 × 10${}^{-14}$	<2 × 10${}^{-16}$	0.2377	0.9584

and

Table A12. Summary of statistically significant differences for serialized model size metric—Breast Cancer dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART
ENORA-RMSE	ENORA-ACC	NSGA-II-AUC	-	-	-	-	-
NSGA-II-RMSE	ENORA-ACC	ENORA-AUC	-	-	NSGA-II-AUC	-	-
PART	ENORA-ACC	ENORA-AUC	-	NSGA-II-ACC	NSGA-II-AUC	-	-
JRip	-	-	JRip	JRip	JRip	JRip	JRip
OneR	OneR	-	OneR	OneR	OneR	OneR	OneR
ZeroR	ZeroR	ZeroR	ZeroR	ZeroR	ZeroR	ZeroR	ZeroR

in Appendix A show the results of the performed tests for the Breast Cancer dataset for each of the three metrics, and

Table A13. Shapiro–Wilk normality test p-values for percent correct metric—Monk’s Problem 2 dataset.

Algorithm	p-Value	Null Hypothesis
ENORA-ACC	0.6543	Not Rejected
ENORA-AUC	0.6842	Not Rejected
ENORA-RMSE	0.0135	Rejected
NSGA-II-ACC	0.979	Not Rejected
NSGA-II-AUC	0.382	Not Rejected
NSGA-II-RMSE	0.0486	Rejected
PART	0.5671	Not Rejected
JRip	0.075	Rejected
OneR	4.672 × 10${}^{-06}$	Rejected
ZeroR	4.672 × 10${}^{-06}$	Rejected

,

Table A14. Friedman p-value for percent correct metric—Monk’s Problem 2 dataset.

	p-Value	Null Hypothesis
Frideman	1.292 × 10${}^{-07}$	Rejected

,

Table A15. Nemenyi post-hoc procedure for percent correct metric—Monk’s Problem 2 dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART	JRip	OneR
ENORA-AUC	0.8363	-	-	-	-	-	-	-	-
ENORA-RMSE	1.0000	0.9471	-	-	-	-	-	-	-
NSGA-II-ACC	0.1907	0.9902	0.3481	-	-	-	-	-	-
NSGA-II-AUC	0.0126	0.6294	0.0342	0.9958	-	-	-	-	-
NSGA-II-RMSE	0.0126	0.6294	0.0342	0.9958	1.0000	-	-	-	-
PART	0.8714	1.0000	0.9631	0.9841	0.5769	0.5769	-	-	-
JRip	2.1 × 10${}^{-06}$	0.0048	1.0 × 10${}^{-05}$	0.1341	0.6806	0.6806	0.0036	-	-
OneR	0.0001	0.0743	0.0006	0.6032	0.9875	0.9875	0.0601	0.9984	-
ZeroR	0.0001	0.0743	0.0006	0.6032	0.9875	0.9875	0.0601	0.9984	1.0000

,

Table A16. Summary of statistically significant differences for percent correct metric—Monk’s Problem 2 dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	PART
NSGA-II-AUC	ENORA-ACC	-	ENORA-RMSE	-
NSGA-II-RMSE	ENORA-ACC	-	ENORA-RMSE	-
JRip	ENORA-ACC	ENORA-AUC	ENORA-RMSE	PART
OneR	ENORA-ACC	-	ENORA-RMSE	-
ZeroR	ENORA-ACC	-	ENORA-RMSE	-

,

Table A17. Shapiro–Wilk normality test p-values for area under the ROC curve metric—Monk’s Problem 2 dataset.

Algorithm	p-Value	Null Hypothesis
ENORA-ACC	0.4318	Not Rejected
ENORA-AUC	0.7044	Not Rejected
ENORA-RMSE	0.0033	Rejected
NSGA-II-ACC	0.3082	Not Rejected
NSGA-II-AUC	0.0243	Rejected
NSGA-II-RMSE	0.7802	Not Rejected
PART	0.1641	Not Rejected
JRip	0.3581	Not Rejected
OneR	0.0000	Rejected
ZeroR	0.0000	Rejected

,

Table A18. Friedman p-value for area under the ROC curve metric—Monk’s Problem 2 dataset.

	p-Value	Null Hypothesis
Frideman	1.051 × 10${}^{-08}$	Rejected

,

Table A19. Nemenyi post-hoc procedure for area under the ROC curve metric—Monk’s Problem 2 dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART	JRip	OneR
ENORA-AUC	0.8363	-	-	-	-	-	-	-	-
ENORA-RMSE	1.0000	0.7054	-	-	-	-	-	-	-
NSGA-II-ACC	0.8870	0.0539	0.9556	-	-	-	-	-	-
NSGA-II-AUC	1.0000	0.8544	1.0000	0.8713	-	-	-	-	-
NSGA-II-RMSE	0.5504	0.0084	0.7054	0.9999	0.5239	-	-	-	-
PART	0.7054	1.0000	0.5504	0.0269	0.7295	0.0036	-	-	-
JRip	0.0238	2.3 × 10${}^{-05}$	0.0482	0.6806	0.0211	0.9471	7.0 × 10${}^{-06}$	-	-
OneR	0.0084	4.7 × 10${}^{-06}$	0.0186	0.4715	0.0073	0.8363	1.4 × 10${}^{-06}$	1.0000	-
ZeroR	0.0084	4.7 × 10${}^{-06}$	0.0186	0.4715	0.0073	0.8363	1.4 × 10${}^{-06}$	1.0000	1.0000

,

Table A20. Summary of statistically significant differences for area under the ROC curve metric—Monk’s Problem 2 dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	PART
NSGA-II-RMSE	-	ENORA-AUC	-	-	-	-	-
PART	-	-	-	PART	-	PART	-
JRip	ENORA-ACC	ENORA-AUC	ENORA-RMSE	-	NSGA-II-AUC	-	PART
OneR	ENORA-ACC	ENORA-AUC	ENORA-RMSE	-	NSGA-II-AUC	-	PART
ZeroR	ENORA-ACC	ENORA-AUC	ENORA-RMSE	-	NSGA-II-AUC	-	PART

,

Table A21. Shapiro–Wilk normality test p-values for serialized model size metric—Monk’s Problem 2 dataset.

Algorithm	p-Value	Null Hypothesis
ENORA-ACC	4.08 × 10${}^{-05}$	Rejected
ENORA-AUC	0.0002	Rejected
ENORA-RMSE	0.0094	Rejected
NSGA-II-ACC	0.0192	Rejected
NSGA-II-AUC	0.0846	Rejected
NSGA-II-RMSE	0.0037	Rejected
PART	0.9721	Not Rejected
JRip	0.0068	Rejected
OneR	0.0000	Rejected
ZeroR	0.0000	Rejected

,

Table A22. Friedman p-value for serialized model size metric—Monk’s Problem 2 dataset.

	p-Value	Null Hypothesis
Frideman	2.657 × 10${}^{-13}$	Rejected

,

Table A23. Nemenyi post-hoc procedure for serialized model size metric—Monk’s Problem 2 dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART	JRip	OneR
ENORA-AUC	1.0000	-	-	-	-	-	-	-	-
ENORA-RMSE	1.0000	1.0000	-	-	-	-	-	-	-
NSGA-II-ACC	1.0000	1.0000	1.0000	-	-	-	-	-	-
NSGA-II-AUC	0.9925	0.9696	0.9984	0.9841	-	-	-	-	-
NSGA-II-RMSE	0.8870	0.9556	0.7966	0.9267	0.2622	-	-	-	-
PART	0.2824	0.1752	0.3957	0.2246	0.9015	0.0027	-	-	-
JRip	0.1752	0.2824	0.1110	0.2246	0.0084	0.9752	1.0 × 10${}^{-05}$	-	-
OneR	0.0211	0.0431	0.0110	0.0304	0.0004	0.6552	1.5 × 10${}^{-07}$	0.9993	-
ZeroR	0.0012	0.0031	0.0006	0.0020	1.0 × 10${}^{-05}$	0.1907	1.3 × 10${}^{-09}$	0.9015	0.9993

and

Table A24. Summary of statistically significant differences for serialized model size metric—Monk’s Problem 2 dataset.

	ENORA-ACC	ENORA-AUC	ENORA-RMSE	NSGA-II-ACC	NSGA-II-AUC	NSGA-II-RMSE	PART
PART	-	-	-	-	-	NSGA-II-RMSE	-
JRip	-	-	-	-	JRip	-	JRip
OneR	OneR	OneR	OneR	OneR	OneR	-	OneR
ZeroR	ZeroR	ZeroR	ZeroR	ZeroR	ZeroR	-	ZeroR

in Appendix B show the results for the Monk’s Problem 2 dataset.

4.7. Additional Experiments

Finally, we show the results of the evaluation with 10-fold cross-validation for Monk’s problem 2 dataset and for the following four other datasets:

• Tic-Tac-Toe-Endgame dataset, with 9 input attributes, 958 instances, and binary class (

  Table 11. Attribute description of the Tic-Tac-Toe-Endgame dataset.

  #	Attribute Name	Type	Possible Values
  1	top-left-square	categorical	x, o, b
  2	top-middle-square	categorical	x, o, b
  3	top-right-square	categorical	x, o, b
  4	middle-left-square	categorical	x, o, b
  5	middle-middle-square	categorical	x, o, b
  6	middle-right-square	categorical	x, o, b
  7	bottom-left-square	categorical	x, o, b
  8	bottom-middle-square	categorical	x, o, b
  9	bottom-right-square	categorical	x, o, b
  10	class	categorical	positive, negative

  ).
• Car dataset, with 6 input attributes, 1728 instances, and 4 output classes (

  Table 12. Attribute description of the Car dataset.

  #	Attribute Name	Type	Possible Values
  1	buying	categorical	vhigh, high, med, low
  2	maint	categorical	vhigh, high, med, low
  3	doors	categorical	2, 3, 4, 5-more
  4	persons	categorical	2, 4, more
  5	lug_boot	categorical	small, med, big
  6	safety	categorical	low, med, high
  7	class	categorical	unacc, acc, good, vgood

  ).
• Chess (King-Rook vs. King-Pawn) (kr-vs-kp), with 36 input attributes, 3196 instances, and binary class (

  Table 13. Attribute description of the kr-vs-kp dataset.

  #	Attribute Name	Type	Possible Values
  1	bkblk	categorical	t, f
  2	bknwy	categorical	t, f
  3	bkon8	categorical	t, f
  4	bkona	categorical	t, f
  5	bkspr	categorical	t, f
  6	bkxbq	categorical	t, f
  7	bkxcr	categorical	t, f
  8	bkxwp	categorical	t, f
  9	blxwp	categorical	t, f
  10	bxqsq	categorical	t, f
  11	cntxt	categorical	t, f
  12	dsopp	categorical	t, f
  13	dwipd	categorical	g, l
  14	hdchk	categorical	t, f
  15	katri	categorical	b, n, w
  16	mulch	categorical	t, f
  17	qxmsq	categorical	t, f
  18	r2ar8	categorical	t, f
  19	reskd	categorical	t, f
  20	reskr	categorical	t, f
  21	rimmx	categorical	t, f
  22	rkxwp	categorical	t, f
  23	rxmsq	categorical	t, f
  24	simpl	categorical	t, f
  25	skach	categorical	t, f
  26	skewr	categorical	t, f
  27	skrxp	categorical	t, f
  28	spcop	categorical	t, f
  29	stlmt	categorical	t, f
  30	thrsk	categorical	t, f
  31	wkcti	categorical	t, f
  32	wkna8	categorical	t, f
  33	wknck	categorical	t, f
  34	wkovl	categorical	t, f
  35	wkpos	categorical	t, f
  36	wtoeg	categorical	n, t, f
  37	class	categorical	won, nowin

  ).
• Nursery dataset, with 8 input attributes, 12,960 instances, and 5 output classes (

  Table 14. Attribute description of the Nursery dataset.

  #	Attribute Name	Type	Possible Values
  1	parents	categorical	usual, pretentious, great_pret
  2	has_nurs	categorical	proper, less_proper, improper, critical, very_crit
  3	form	categorical	complete, completed, incomplete, foster
  4	children	categorical	1, 2, 3, more
  5	housing	categorical	convenient, less_conv, critical
  6	finance	categorical	convenient, inconv
  7	social	categorical	nonprob, slightly_prob, problematic
  8	health	categorical	recommended, priority, not_recom
  9	class	categorical	not_recom, recommend, very_recom, priority, spec_prior

  ).

We have used the ENORA algorithm together with the ${\mathcal{ACC}}_{\mathcal{D}}$ and ${\mathcal{RMSE}}_{\mathcal{D}}$ objective functions in this case because these combinations have produced the best results for the Breast Cancer and Monk’s problem 2 datasets evaluated in 10-fold cross-validation (population size equal to 50, 20,000 generations and $M_{max}=10+$ number of classes).

Table 15. Comparison of the performance of the learning models in 10-fold cross-validation mode—Monk’s Problem 2, Tic-Tac-Toe-Endgame, Car, kr-vs-kp and Nursery datasets.

Learning Model	Number of Rules	Percent Correct	TP Rate	FP Rate	Precision	Recall	F-Measure	MCC	ROC Area	PRC Area	RMSE
Monk’s problem 2
ENORA-ACC	7	77.70	0.777	0.360	0.777	0.777	0.762	0.481	0.708	0.695	0.472
PART	47	79.53	0.795	0.253	0.795	0.795	0.795	0.544	0.884	0.893	0.380
JRip	1	62.90	0.629	0.646	0.526	0.629	0.535	−0.034	0.478	0.537	0.482
OneR	1	65.72	0.657	0.657	0.432	0.657	0.521	0.000	0.500	0.549	0.586
ZeroR	-	65.72	0.657	0.657	0.432	0.657	0.521	0.000	0.491	0.545	0.457
Tic-Tac-Toe-Endgame
ENORA-ACC/RMSE	2	98.33	0.983	0.031	0.984	0.983	0.983	0.963	0.976	0.973	0.129
PART	49	94.26	0.943	0.076	0.942	0.943	0.942	0.873	0.974	0.969	0.220
JRip	9	97.81	0.978	0.031	0.978	0.978	0.978	0.951	0.977	0.977	0.138
OneR	1	69.94	0.699	0.357	0.701	0.699	0.700	0.340	0.671	0.651	0.548
ZeroR	-	65.35	0.653	0.653	0.427	0.653	0.516	0.000	0.496	0.545	0.476
Car
ENORA-RMSE	14	86.57	0.866	0.089	0.866	0.866	0.846	0.766	0.889	0.805	0.259
PART	68	95.78	0.958	0.016	0.959	0.958	0.958	0.929	0.990	0.979	0.1276
JRip	49	86.46	0.865	0.064	0.881	0.865	0.870	0.761	0.947	0.899	0.224
OneR	1	70.02	0.700	0.700	0.490	0.700	0.577	0.000	0.500	0.543	0.387
ZeroR	-	70.02	0.700	0.700	0.490	0.700	0.577	0.000	0.497	0.542	0.338
kr-vs-kp
ENORA-RMSE	10	94.87	0.949	0.050	0.950	0.949	0.949	0.898	0.950	0.927	0.227
PART	23	99.06	0.991	0.010	0.991	0.991	0.991	0.981	0.997	0.996	0.088
JRip	16	99.19	0.992	0.008	0.992	0.992	0.992	0.984	0.995	0.993	0.088
OneR	1	66.46	0.665	0.350	0.675	0.665	0.655	0.334	0.657	0.607	0.579
ZeroR	-	52.22	0.522	0.522	0.273	0.522	0.358	0.000	0.499	0.500	0.500
Nursery
ENORA-ACC	15	88.41	0.884	0.055	0.870	0.884	0.873	0.824	0.915	0.818	0.2153
PART	220	99.21	0.992	0.003	0.992	0.992	0.992	0.989	0.999	0.997	0.053
JRip	131	96.84	0.968	0.012	0.968	0.968	0.968	0.957	0.993	0.974	0.103
OneR	1	70.97	0.710	0.137	0.695	0.710	0.702	0.570	0.786	0.632	0.341
ZeroR	-	33.33	0.333	0.333	0.111	0.333	0.167	0.000	0.500	0.317	0.370

shows the results of the best combination ENORA-ACC or ENORA-RMSE together with the results of the classical rule-based classifiers.

5. Analysis of Results and Discussion

The results of our tests allow for several considerations. The first interesting observation is that NSGA-II identifies fewer solutions than ENORA on the Pareto front, which implies less diversity and therefore a worse hypervolume ratio, as shown in Figure 3 and Figure 4. This is not surprising: in several other occasions [19,34,60], it has been shown that ENORA maintains a higher diversity in the population than other well-known evolutionary algorithms, with generally positive influence on the final results. Comparing the results in full training mode against the results in cross-validation or in splitting mode makes it evident that our solution produces classification models that are more resilient to over-fitting. For example, the classifier learned by PART with Monk’s Problem 2 presents a 94.01% accuracy in full training mode that drops to 73.51% in splitting mode. A similar, although with a more contained drop in accuracy, is shown by the classifier learned with Breast Cancer dataset; at the same time, the classifier learned by ENORA driven by accuracy shows only a 5.57% drop in one case, and even an improvement in the other case (see Table 5, Table 6, Table 9, and Table 10). This phenomenon is easily explained by looking at the number of rules: the more rules in a classifier, the higher the risk of over-fitting; PART produces very accurate classifiers, but at the price of adding many rules, which not only affects the interpretability of the model but also its resilience to over-fitting. Full training results seem to indicate that when the optimization model is driven by RMSE the classifiers are more accurate; nevertheless, they are also more prone to over-fitting, indicating that, on average, the optimization models driven by the accuracy are preferable.

From the statistical tests (whose results are shown in the Appendix A and Appendix B) we conclude that among the six variants of the proposed optimization model there are no statistical significative differences, which suggests that the advantages of our method do not depend directly on a specific evolutionary algorithm or on the specific performance measure that is used to drive the evolutions. Significant statistical differences between our method and very simple classical methods such as OneR were expectable. Significant statistical differences between our method and a well-consolidated one such as PART have not been found, but the price to be paid for using PART in order to have similar results to ours is a very high number of rules (15 vs. 2 in one case and 47 vs. 7 in the other case).

We would like to highlight that both the Breast Cancer dataset and the Monk’s problem 2 dataset are difficult to approximate with interpretable classifiers and that none of the analyzed classifiers obtains high accuracy rates using the cross-validation technique. Even powerful black-box classifiers, such as Random Forest and Logistic, obtain success rates below $70\%$ in 10-fold cross-validation for these datasets. However, ENORA obtains a better balance (trade-off) between precision and interpretability than the rest of the classifiers. For the rest of the analyzed datasets, the accuracy obtained using ENORA is substantially higher. For example, for the Tic-Tac-Toe-Endgame dataset, ENORA obtains a $98.3299\%$ success percentage with only two rules in cross-validation, while PART obtains $94.2589\%$ with 49 rules, and JRip obtains $97.8079\%$ with nine rules. With respect to the results obtained in the datasets Car, kr-vs-kp and Nursery, we want to comment that better success percentage can be obtained if the maximum number of evaluations is increased. However, better success percentages imply a greater number of rules, which is to the detriment of the interpretability of the models.

6. Conclusions and Future Works

In this paper, we have proposed a novel technique for categorical classifier learning. Our proposal is based on defining the problem of learning a classifier as a multi-objective optimization problem, and solving it by suitably adapting an evolutionary algorithm to this task; our two objectives are minimizing the number of rules (for a better interpretability of the classifier) and maximizing a metric of performance. Depending on the particular metric that is chosen, (slightly) different optimization models arise. We have tested our proposal, in a first instance, on two different publicly available datasets, Breast Cancer (in which each instance represents a patient that has suffered from breast cancer and is described by nine attributes, and the class to be predicted represents the fact that the patient has suffered a recurring event) and Monk’s Problem 2 (which is an artificial, well-known dataset in which the class to be predicted represents a logical function), using two different evolutionary algorithms, namely ENORA and NSGA-II, and three different choices as a performance metric, i.e., accuracy, the area under the ROC curve, and the root mean square error. Additionally, we have shown the results of the evaluation in 10-fold cross-validation of the publicly available Tic-Tac-Toe-Endgame, Car, kr-vs-kp and Nursery datasets.

Our initial motivation was to design a classifier learning system that produces interpretable, yet accurate, classifiers: since interpretability is a direct function of the number of rules, we conclude that such an objective has been achieved. As an aside, observe that our approach allows the user to decide, beforehand, a maximum number of rules; this can also be done in PART and JRip, but only indirectly. Finally, the idea underlying our approach is that multiple classifiers are explored at the same time in the same execution, and this allows us to choose the best compromise between the performance and the interpretability of a classifier a posteriori.

As a future work, we envisage that our methodology can benefit from an embedded future selection mechanism. In fact, all attributes are (ideally) used in every rule of a classifier learned by our optimization model. By simply relaxing such a constraint, and by suitably re-defining the first objective in the optimization model (e.g., by minimizing the sum of the lengths of all rules, or similar measures), the resulting classifiers will naturally present rules that use more features as well as rules that use less (clearly, the implementation must be adapted to obtain an initial population in which the classifiers have rules of different lengths as well as mutation operators that allow a rule to grow or to shrink). Although this approach does not follow the classical definition of feature selection mechanisms (in which a subset of features is selected that reduces the dataset over which a classifier is learned), it is natural to imagine that it may produce even more accurate classifiers, and more interpretable at the same time.

Currently, we are implementing our own version of multi-objective differential evolution (MODE) for rule-based classification for inclusion in the Weka Open Source Software issued under the GNU General Public License. The implementation of other algorithms, such as MOEA/D, their adaptation in the Weka development platform and subsequent analysis and comparison are planned for future work.