Physical-Layer Security Analysis over M-Distributed Fading Channels
Abstract
:1. Introduction
- Under the M-distributed fading channel, the exact expression of the SOP is first derived. To reduce computational complexity, a closed-form expression for the lower bound of the SOP is obtained. It is shown that the performance gap between the exact SOP expression and its lower bound is small in the high signal-to-noise ratio (SNR) regime.
- The closed-form expression for the probability of the SPSC over the M-distributed fading channel is derived. It is found that when the target secrecy rate is set to be zero, the lower bound of SOP has the same expression as the probability of the SPSC.
- Over the M-distributed fading channel, the exact expression of the ESC with a double integral is obtained. To obtain a closed-form expression, the lower bound of ESC is then derived. It is shown that the performance gap between the exact expression and the lower bound of the ESC is small.
- As special cases of the M fading channel, the secure performance over the K, exponential, and Gamma-Gamma fading channels is derived, respectively. The accuracy of these performance analysis is verified by simulations.
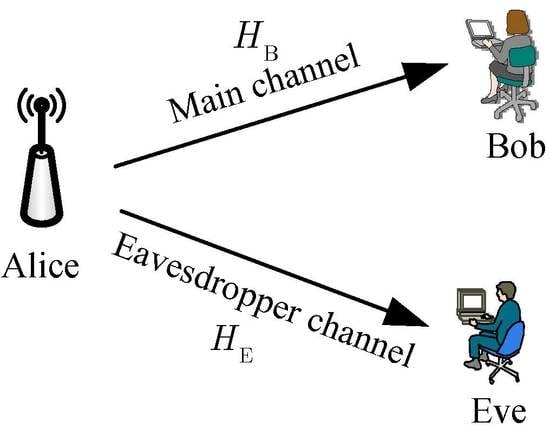
2. System Model
3. Secrecy Performance Analysis
3.1. SOP Analysis
3.2. Probability of SPSC Analysis
3.3. ESC Analysis
4. Some Special Cases
4.1. K Distribution Channel
4.2. Exponential Distribution Channel
4.3. Gamma-Gamma Distribution Channels
4.4. Other Channels
5. Numerical Results
5.1. SOP Results
5.2. Probability of SPSC Results
5.3. ESC Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, J.; Tejedor, E.; Ranta-aho, K.; Wang, H.; Lee, K.-T.; Semaan, E.; Mohyeldin, E.; Song, J.; Bergljung, C.; Jung, S. Spectrum for 5G: Global status, challenges, and enabling technologies. IEEE Commun. Mag. 2018, 56, 12–18. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Ge, H.; Lin, M.; Wang, J.-B.; Dai, J.; Alouini, M.-S. On the secrecy rate of spatial modulation-based indoor visible light communications. IEEE J. Sel. Areas Commun. 2019, 37, 2087–2101. [Google Scholar] [CrossRef]
- Dacier, M.C.; Konjg, H.; Cwalinski, R.; Kargl, F.; Dietrich, S. Security challenges and opportunities of software-defined networking. IEEE Secur. Priv. 2017, 15, 96–100. [Google Scholar] [CrossRef]
- Chen, X.; Ng, D.W.K.; Gerstacker, W.H.; Chen, H.-H. A survey on multiple-antenna techniques for physical layer security. IEEE Commun. Surv. Tutor. 2017, 19, 1027–1053. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Liu, C.; Wang, J.-B.; Wu, Y.; Lin, M.; Cheng, J. Physical-layer security for indoor visible light communications: Secrecy capacity analysis. IEEE Trans. Commun. 2018, 66, 6423–6436. [Google Scholar] [CrossRef]
- Nguyen, V.-D.; Hoang, T.M.; Shin, O.-S. Secrecy capacity of the primary system in a cognitive radio network. IEEE Trans. Veh. Technol. 2015, 64, 3834–3843. [Google Scholar] [CrossRef]
- Ji, S.; Wang, W.-Q.; Chen, H.; Zhang, S. On physical-layer security of FDA communications over Rayleigh fading channels. IEEE Trans. Cogn. Commun. Netw. 2019, 5, 476–490. [Google Scholar] [CrossRef]
- Omri, A.; Hasna, M.O. Average secrecy outage rate and average secrecy outage duration of wireless communication systems with diversity over Nakagami-m fading channels. IEEE Trans. Wirel. Commun. 2018, 17, 3822–3833. [Google Scholar] [CrossRef]
- Lei, H.; Gao, C.; Guo, Y.; Pan, G. On physical layer security over generalized Gamma fading channels. IEEE Commun. Lett. 2015, 19, 1257–1260. [Google Scholar] [CrossRef]
- Liu, X. Probability of strictly positive secrecy capacity of the Rician-Rician fading channel. IEEE Commun. Lett. 2013, 2, 50–53. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, H. An upper bound on the capacity of distributed MIMO systems with Rician/Lognormal fading. IEEE Commun. Lett. 2016, 20, 312–315. [Google Scholar] [CrossRef]
- Ansari, I.S.; Alouini, M.-S.; Cheng, J. Ergodic capacity analysis of free-space optical links with nonzero boresight pointing errors. IEEE Trans. Wirel. Commun. 2015, 14, 4248–4264. [Google Scholar] [CrossRef]
- Hwang, Y.M.; Kim, E.C.; Kim, J.Y. Performance analysis of PN code acquisition with MIMO scheme for an UWB TH/CDMA system. Wirel. Commun. Mobil. Comp. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Liu, X. Outage probability of secrecy capacity over correlated lognormal fading channels. IEEE Commun. Lett. 2013, 17, 289–292. [Google Scholar] [CrossRef]
- Pan, G.; Tang, C.; Zhang, X.; Li, T.; Weng, Y.; Chen, Y. Physical-layer security over non-small-scale fading channels. IEEE Trans. Veh. Technol. 2016, 65, 1326–1339. [Google Scholar] [CrossRef]
- Lei, H.; Zhang, H.; Ansari, I.S.; Gao, C.; Guo, Y.; Pan, G.; Qaraqe, K.A. Performance analysis of physical layer security over generalized-K fading channels using a mixture Gamma distribution. IEEE Commun. Lett. 2016, 20, 408–411. [Google Scholar] [CrossRef]
- Bhargav, N.; Cotton, S.L.; Simmons, D.E. Secrecy capacity analysis over k-μ fading channels: Theory and applications. IEEE Trans. Commun. 2016, 64, 3011–3024. [Google Scholar] [CrossRef]
- Ansari, I.S.; Yilmaz, F.; Alouini, M.-S. Performance analysis of free-space optical links over Malaga (M) turbulence channels with pointing errors. IEEE Trans. Wirel. Commun. 2016, 15, 91–102. [Google Scholar] [CrossRef]
- Jurado-Navas, A.; Garrido-Balsells, J.M.; Paris, J.F.; Castillo-Vazquez, M.; Puerta-Notario, A. General analytical expressions for the bit error rate of atmospheric optical communication systems. Opt. Lett. 2011, 36, 4095–4097. [Google Scholar] [CrossRef]
- Wang, J.-Y.; Wang, J.-B.; Chen, M.; Tang, Y.; Zhang, Y. Outage analysis for relay-aided free-space optical communications over turbulence channels with nonzero boresight pointing errors. IEEE Photon. J. 2014, 6, 1–15. [Google Scholar]
- Garrido-Balsells, J.M.; Jurado-Navas, A.; Paris, J.F.; Castillo-Vazquez, M.; Puerta-Notario, A. On the capacity of M-distributed atmospheric optical channels. Opt. Lett. 2013, 38, 3984–3987. [Google Scholar] [CrossRef] [PubMed]
- Miridakis, N.I.; Tsiftsis, T.A. EGC reception for FSO systems under mixture-Gamma fading channels and pointing errors. IEEE Commun. Lett. 2017, 21, 1441–1444. [Google Scholar] [CrossRef]
- Singh, R.; Rawat, M. Performance analysis of physical layer security over Weibull/lognormal composite fading channel with MRC reception. Int. J. Electron. Commun. 2019, 110, 1–13. [Google Scholar] [CrossRef]
- Adamchik, V.S.; Marichev, O.I. The algorithm for calculating integrals of hypergeometric type functions and its realization in REDUCE system. In Proceedings of the the International Symposium on Symbolic and Algebraic Computation, Tokyo, Japan, 20–24 August 1990; pp. 212–224. [Google Scholar]
- Wang, J.-Y.; Lin, S.-H.; Cai, W.; Dai, J. ESR analysis over ST-MRC MIMO Nakagami fading channels. IET Inf. Secur. 2019, 13, 420–425. [Google Scholar] [CrossRef]











| Distribution Models | Generation |
|---|---|
| K distribution | , |
| Exponential distribution | , , |
| Gamma-Gamma distribution | , |
| Lognormal distribution | , , |
| Gamma-Rician distribution | |
| Gamma distribution | , |
| Rice-Nakagami distribution | , |
| 10 dB | 20 dB | 30 dB | 40 dB | 50 dB | |
|---|---|---|---|---|---|
| 3.699% | 3.205% | 1.880% | 1.936% | 0.293% | |
| 0.436% | 0.041% | 0.795% | 0.651% | 0.156% |
| 10 dB | 20 dB | 30 dB | 40 dB | 50 dB | |
|---|---|---|---|---|---|
| 0.780% | 0.125% | 7.777% | 6.753% | 2.283% |
| 25 dB | 30 dB | 35 dB | 40 dB | 45 dB | 50 dB | |
|---|---|---|---|---|---|---|
| 31.911% | 11.668% | 3.879% | 1.845% | 0.713% | 0.195% | |
| 3.112% | 0.401% | 0.419% | 0.258% | 0.221% | 0.450% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, S.-H.; Lu, R.-R.; Fu, X.-T.; Tong, A.-L.; Wang, J.-Y. Physical-Layer Security Analysis over M-Distributed Fading Channels. Entropy 2019, 21, 998. https://doi.org/10.3390/e21100998
Lin S-H, Lu R-R, Fu X-T, Tong A-L, Wang J-Y. Physical-Layer Security Analysis over M-Distributed Fading Channels. Entropy. 2019; 21(10):998. https://doi.org/10.3390/e21100998
Chicago/Turabian StyleLin, Sheng-Hong, Rong-Rong Lu, Xian-Tao Fu, An-Ling Tong, and Jin-Yuan Wang. 2019. "Physical-Layer Security Analysis over M-Distributed Fading Channels" Entropy 21, no. 10: 998. https://doi.org/10.3390/e21100998
APA StyleLin, S. -H., Lu, R. -R., Fu, X. -T., Tong, A. -L., & Wang, J. -Y. (2019). Physical-Layer Security Analysis over M-Distributed Fading Channels. Entropy, 21(10), 998. https://doi.org/10.3390/e21100998