Unusual Quantum Transport Mechanisms in Silicon Nano-Devices
Abstract
:1. Introduction
2. Introduction to New Results
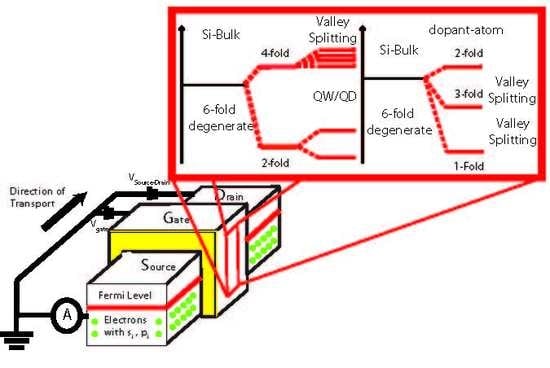
2.1. Special Properties of the Electrons in Silicon CMOS Compatible Devices
2.2. Kondo Effects in Silicon Nanostructures
More about These Kondo Effects
- (a)
- For conventional semiconductors, the Kondo effect has only been observed in relation to interactions between the spin of electrons confined within the localized state and the ones of the surrounding free electrons at sufficiently low temperatures (T’s), i.e., for Temperature < Kondo temperature (TKondo), see Reference [32]. This situation is illustrated in Figure 4a, and as shown in Figure 4b, in this situation, the spin-Kondo effect is suppressed when a sufficiently high magnetic field is applied to the system because the Zeeman splitting between the spin up and the spin down of the electrons makes energetically impossible for spin fluctuations to generate virtual states that would open the Kondo transport channel [32]. This situation goes also under the name of conventional SU(2) Spin Kondo effect.
- (b)
- In materials were the pseudo-spin degree of freedom is also available, however, as in the area in Figure 3 outlined by the rectangular shaded shape and as illustrated in Figure 4c, the Kondo effect is somehow different to the one shown in Figure 4a and as described in the above sections. A different situation from the one above has recently been observed and is evident both from the experimental and from the theoretical points of view in silicon CMOS three terminal devices [8,9]. The extension of the Kondo effect to valley-orbital degree of freedom is clearly illustrated in Figure 4c by introducing different colors (black and red) for the two-different valley-orbital levels involved in the effect, i.e., the two lowest states, as shown as degenerate in Figure 4c,d. Consequently, the Kondo effect observed in silicon nanostructures is a more sophisticated phenomenon that goes under the name of SU(4) Kondo effect [4,8,9].
2.3. Kondo-Fano Effects in Silicon Nanostructures
2.4. Charge Pumping Effects in Silicon Nanostructures: Single Electron Pumps
2.5. Errors during the Operations of Single Electron Pumps
- (a)
- The first mechanism of error is the one that becomes important when the temperature of operation (T) of the single electron pump is energetically comparable to the charging energy (EC) of the confined states, i.e., EC ≈ KBT, with the charging energy being the energy that the system must pay to increase by one electron the number of electrons in the localized state between the two gates, i.e., from N to N + 1. These thermal effects could lead to losing control of many electrons in each step of the cycle described in Figure 7. The probability of the occurrence of this type of errors is linked to the formula Hence EC >> KBT means that this probability is almost zero. As KBT~24 meV for T = 300 K and ~0.24 meV for T = 3 K, the typical EC~30–50 meV observed in single impurity/atom systems makes that these are immune to temperature errors even when they are operated above the liquid Helium temperatures (≥4.2 K). This explains why single-atom based single electron pumps (SAP’s) are extremely advantageous, as they do not need to be kept at ultra-low temperatures (<1 K) to operate in an environment completely immune from detrimental temperature effects/errors [12,13]. QD electron pumps are often limited in this sense as EC for these systems is often limited to less than a few meV and as such require some complicated sub-kelvin temperature of operations to demonstrate their best performances [14]. However, as soon as the EC of a QD increase to a value like the ones observed naturally in isolated single atom systems, for example by electrostatic confinements [14,47], these errors can also be suppressed in QDs electron pumps operating at temperatures ~4.2 K [14,15].
- (b)
- Another mechanism of errors that can affect single electron pumps, when they operate slightly above the 100 MHz frequencies of excitation, is the one related to non-adiabatic effects [45,48]. These errors are related to the poor efficiency in the achievement of the second step of the pumping cycle, as described in Figure 7b, i.e., the isolation step. This poor efficiency can be observed when the rates that control the back-tunneling of the electrons from the localized state back to the source, Γback’s, allow the escape of the electrons to the source before the full isolation or before the emission to the drain [46,47,48]. This kind of error can particularly affect QD electron pumps as, for these systems, electrons are strongly affected when fast perturbations are exciting the system. At high frequencies of operations, these excitations, i.e., non-adiabatic excitations [48], can lead to the delocalization of electrons between the ground-state and the excited states and as for QDs the rates that govern the tunneling between the excites state and the source/drain leads are fast, if compared to the ones between the ground state and the source/drain leads, hence, when electrons are delocalized, their probability of non-completion of the isolation step is much higher than normal [40,48]. Ultimately, this could lead to errors since it means that electrons will not be emitted to the drain and will not complete their cycle [48].
- (c)
- The alternative way to operate a SAP described above can be relatively error-free, unless these systems are excited to frequencies considerably higher than the GHz ones [12,13]. Consequently, the discussion above opens the way to the description of another kind of errors that could arise in QD or in single atom pumps [13] when electrons reach the confinement potential via an excited state and not the ground state. If the f = 1/τ approaches the values of Γrelaxation described in Figure 7, see also Reference [13]. In this situation, the electrons do not have sufficient time to relax to the ground state and the completion of the isolation step is compromised. The picture above can also be used to understand the causes of errors and of the degradation of the precision/accuracy of the measured currents in SAP’s [13].
- (d)
- Lastly, I would like to briefly discuss another possible mechanism of error that can cause the degradation of the current and which has recently been observed in a silicon QD system [15]. For a system where a QD pump is operating at ultra-fast frequencies of excitations (up to 3.55 GHz), it has been shown that the ideal behavior of the pump can sometimes be affected by errors that appear when an impurity-trap state can compete with the main QD in the capture and in the emission of the electrons [15]. Note that the eventual presence of impurity-trap states in the gate stack of silicon devices is a well-known fact [1,4,45]. This novel frequency dependent mechanism [15], has not been completely explained, and it is a reminder that for silicon CMOS compatible technology, although extremely controlled and reliable [4,5], it is still possible to observe some unexpected behaviors. It is however comforting to note that the hybrid dot-impurity systems, such as the one discussed in this Refs. [15,45], have recently been able to provide record high performances in term of frequency and accuracy of operations [15,50,51,52,53], but have also opened up the way to the use of the quantum pumping technology for novel quantum information schemes [45].
3. Conclusions
Conflicts of Interest
References
- Sze, S.M.; Kwok, K.N. Physics of Semiconductor Devices, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; pp. 7–75. ISBN 9780471143239. [Google Scholar]
- Ramdas, A.K.; Rodriguez, S. Spectroscopy of the solid-state analogues of the hydrogen atom: Donors and acceptors in semiconductors. Rep. Prog. Phys. 1981, 44, 1297–1387. [Google Scholar] [CrossRef]
- Cardona, M.; Yu, P.Y. Fundamentals of Semiconductors, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2010; ISBN 978-3-642-00710-1. [Google Scholar]
- Zwanenburg, F.A.; Dzurak, A.S.; Morello, A.; Simmons, M.Y.; Hollenberg, L.C.L.; Klimeck, G.; Rogge, S.; Coppersmith, S.N.; Eriksson, M.A. Silicon quantum electronics. Rev. Mod. Phys. 2013, 85, 961–1019. [Google Scholar] [CrossRef]
- Jehl, X.; Niquet, Y.-M.; Sanquer, M. Single donor electronics and quantum functionalities with advanced CMOS technology. J. Phys. Condens. Matter 2016, 28, 103001–103018. [Google Scholar] [CrossRef] [PubMed]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K.; Novoselov, K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef] [Green Version]
- Laird, E.A.; Kuemmeth, F.; Steele, G.A.; Grove-Rasmussen, K.; Nygård, J.; Flensberg, K.; Kouwenhoven, L.P. Quantum transport in carbon nanotubes. Rev. Mod. Phys. 2015, 87, 703–764. [Google Scholar] [CrossRef] [Green Version]
- Tettamanzi, G.C.; Verduijn, J.; Lansbergen, G.P.; Blaauboer, M.; Calderon, M.J.; Aguado, R.; Rogge, S. Magnetic-Field Probing of an SU(4) Kondo Resonance in a Single-Atom Transistor. Phys. Rev. Lett. 2012, 108, 046803–046807. [Google Scholar] [CrossRef] [PubMed]
- Lansbergen, G.P.; Tettamanzi, G.C.; Verduijn, J.; Collaert, N.; Biesemans, S.; Blaauboer, M.; Rogge, S. Tunable Kondo Effect in a Single Donor Atom. Nano Lett. 2010, 10, 455–460. [Google Scholar] [CrossRef]
- Verduijn, J.; Tettamanzi, G.C.; Lansbergen, G.P.; Collaert, N.; Biesemans, S.; Rogge, S. Coherent transport through a double donor system in silicon. Appl. Phys. Lett. 2010, 96, 072110–072112. [Google Scholar] [CrossRef]
- Verduijn, J.; Agundez, R.R.; Blaauboer, M.; Rogge, S. Non-local coupling of two donor-bound electrons. New J. Phys. 2013, 15, 033020–033030. [Google Scholar] [CrossRef]
- Tettamanzi, G.C.; Wacquez, R.; Rogge, S. Charge pumping through a single donor atom. New J. Phys. 2013, 16, 063036–063052. [Google Scholar] [CrossRef]
- Van Der Heijden, J.; Tettamanzi, G.C.; Rogge, S. Dynamics of a single-atom electron pump. Sci. Rep. 2017, 7, 44371. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rossi, A.; Tanttu, T.; Tan, K.Y.; Iisakka, I.; Zhao, R.; Chan, K.W.; Tettamanzi, G.C.; Rogge, S.; Dzurak, A.S.; Möttönen, M. An Accurate Single-Electron Pump Based on a Highly Tunable Silicon Quantum Dot. Nano Lett. 2014, 14, 3405–3411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rossi, A.; Klochan, J.; Timoshenko, J.; Hudson, F.E.; Möttönen, M.; Rogge, S.; Dzurak, A.S.; Kashcheyevs, V.; Tettamanzi, G.C. Gigahertz Single-Electron Pumping Mediated by Parasitic States. Nano Lett. 2018, 18, 4141–4147. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sellier, H.; Lansbergen, G.P.; Caro, J.; Rogge, S.; Collaert, N.; Ferain, I.; Jurczak, M.; Biesemans, S. Transport Spectroscopy of a Single Dopant in a Gated Silicon Nanowire. Phys. Rev. Lett. 2006, 97, 206805–206808. [Google Scholar] [CrossRef] [PubMed]
- Lansbergen, G.P.; Rahman, R.; Wellard, C.J.; Woo, I.; Caro, J.; Collaert, N.; Biesemans, S.; Klimeck, G.; Hollenberg, L.C.L.; Rogge, S. Gate-induced quantum-confinement transition of a single dopant atom in a silicon FinFET. Nat. Phys. 2008, 4, 656–661. [Google Scholar] [CrossRef]
- Griffiths, D.J. Introduction to Quantum Mechanics, 2nd ed.; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005; ISBN 0131118927. [Google Scholar]
- Trocha, G.C. Orbital Kondo effect in double quantum dots. Phys. Rev. B 2010, 82, 125323–125332. [Google Scholar] [CrossRef]
- Mi, X.; Kohler, S.; Petta, J.R. Landau-Zener interferometry of valley-orbit states in Si/SiGe double quantum dots. Phys. Rev. B 2018, 98, 161404. [Google Scholar] [CrossRef] [Green Version]
- Pierre, M.; Wacquez, R.; Jehl, X.; Sanquer, M.; Vinet, M.; Cueto, O. Single donor ionization energies in a nanoscale CMOS channel. Nat. Nanotechnol. 2010, 5, 133–137. [Google Scholar] [CrossRef]
- Fuechsle, M.; Miwa, J.A.; Mahapatra, S.; Ryu, H.; Lee, S.; Warschkow, O.; Hollenberg, L.C.L.; Klimeck, G.; Simmons, M.Y. A single-atom transistor. Nat. Nanotechnol. 2012, 7, 242–246. [Google Scholar] [CrossRef]
- Tan, K.Y.; Chan, K.W.; Möttönen, M.; Morello, A.; Yang, C.; Van Donkelaar, J.; Alves, A.; Pirkkalainen, J.-M.; Jamieson, D.N.; Clark, R.G.; et al. Transport Spectroscopy of Single Phosphorus Donors in a Silicon Nanoscale Transistor. Nano Lett. 2010, 10, 11–15. [Google Scholar] [CrossRef]
- Tettamanzi, G.C.; Hile, S.J.; House, M.G.; Fuechsle, M.; Rogge, S.; Simmons, M.Y. Correction to Probing the Quantum States of a Single Atom Transistor at Microwave Frequencies. ACS Nano 2017, 11, 2444–2451. [Google Scholar] [CrossRef] [PubMed]
- Van der Heijden, J.; Salfi, J.; Mol, J.A.; Verduijn, J.; Tettamanzi, G.C.; Hamilton, A.R.; Collaert, N.; Rogge, S. Probing the Spin States of a Single Acceptor Atom. Nano Lett. 2014, 14, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Prati, E.; Shinada, T. Single-Atom Nano-electronics; Pan Stanford: Singapore, 2013; ISBN 9789814316316. [Google Scholar]
- Collaert, N. CMOS Nano-Electronics: Innovative Devices, Architectures, and Applications; Pan Stanford: Singapore, 2012; ISBN 9789814364027. [Google Scholar]
- Lansbergen, G.P.; Rahman, R.; Verduijn, J.; Tettamanzi, G.C.; Collaert, N.; Biesemans, S.; Klimeck, G.; Hollenberg, L.C.L.; Rogge, S. Lifetime-Enhanced Transport in Silicon due to Spin and Valley Blockade. Phys. Rev. Lett. 2011, 107, 136602. [Google Scholar] [CrossRef] [PubMed]
- Tettamanzi, G.C.; Paul, A.; Lansbergen, G.; Verduijn, J.; Lee, S.; Collaert, N.; Biesemans, S.; Klimeck, G.; Rogge, S. Thermionic Emission as a Tool to Study Transport in Undoped nFinFETs. IEEE Electron Device Lett. 2010, 31, 150–152. [Google Scholar] [CrossRef]
- Wacquez, R.; Vinet, M.; Pierre, M.; Roche, B.; Jehl, X.; Cueto, O.; Verduijn, J.; Tettamanzi, G.C.; Rogge, S.; Deshpande, V.; et al. Single dopant impact on electrical characteristics of SOI NMOSFETs with effective length down to 10nm. In Proceedings of the 2010 Symposium on VLSI Technology, Honolulu, HI, USA, 15–17 June 2010. [Google Scholar] [CrossRef]
- Seo, M.; Roulleau, P.; Roche, P.; Glattli, D.C.; Sanquer, M.; Jehl, X.; Hutin, L.; Barraud, S.; Parmentier, F.D. Strongly Correlated Charge Transport in Silicon Metal-Oxide-Semiconductor Field-Effect Transistor Quantum Dots. Phys. Rev. Lett. 2018, 121, 027701–027705. [Google Scholar] [CrossRef] [PubMed]
- Cronenwett, S.M. A Tunable Kondo Effect in Quantum Dots. Science 1998, 281, 540–544. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rokhinson, L.P.; Guo, L.J.; Chou, S.Y.; Tsui, D.C. Kondo-like zero-bias anomaly in electronic transport through an ultrasmall Si quantum dot. Phys. Rev. B 1999, 60, R16319–R16321. [Google Scholar] [CrossRef] [Green Version]
- Sasaki, S.; De Franceschi, S.; Elzerman, J.M.; Van der Wiel, W.G.; Eto, M.; Tarucha, S.; Kouwenhoven, L. Kondo effect in an integer-spin quantum dot. Nature 2000, 405, 764–767. [Google Scholar] [CrossRef] [Green Version]
- Gavai, R.V. On the deconfinement transition in SU(4) lattice gauge theory. Nucl. Phys. B 2002, 633, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866–1878. [Google Scholar] [CrossRef]
- Aharonov, Y.; Bohm, D. Significance of Electromagnetic Potentials in the Quantum Theory. Phys. Rev. 1959, 115, 485–491. [Google Scholar] [CrossRef]
- Thouless, D.J. Quantization of particle transport. Phys. Rev. B 1983, 27, 6083–6087. [Google Scholar] [CrossRef]
- Maire, N.; Hohls, F.; Kaestner, B.; Pierz, K.; Schumacher, H.W.; Haug, R.J. Noise measurement of a quantized charge pump. Appl. Phys. Lett. 2008, 92, 082112–082115. [Google Scholar] [CrossRef]
- Kaestner, B.; Kashcheyevs, V. Non-adiabatic quantized charge pumping with tunable-barrier quantum dots: A review of current progress. Rep. Prog. Phys. 2015, 78, 103901. [Google Scholar] [CrossRef] [PubMed]
- Ubbelohde, N.; Hohls, F.; Kashcheyevs, V.; Wagner, T.; Fricke, L.; Kästner, B.; Pierz, K.; Schumacher, H.W.; Haug, R.J. Partitioning of on-demand electron pairs. Nat. Nanotechnol. 2015, 10, 46–49. [Google Scholar] [CrossRef] [PubMed]
- Bauerle, C.; Glattli, D.C.; Meunier, T.; Portier, F.; Roche, P.; Roulleau, P.; Takada, S.; Waintal, X.; Glattli, C. Coherent control of single electrons: A review of current progress. Rep. Prog. Phys. 2018, 81, 056503. [Google Scholar] [CrossRef] [PubMed]
- Bocquillon, E.; Parmentier, F.; Grenier, C.; Berroir, J.-M.; DeGiovanni, P.; Glattli, D.C.; Placais, B.; Cavanna, A.; Jin, Y.; Feve, G. Electron Quantum Optics: Partitioning Electrons One by One. Phys. Rev. Lett. 2012, 108, 196803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Okazaki, Y.; Nakamura, S.; Onomitsu, K.; Kaneko, N.-H. Digital processing with single electrons for arbitrary waveform generation of current. Appl. Phys. Express 2018, 11, 036701–036704. [Google Scholar] [CrossRef]
- Yamahata, G.; Ryu, S.; Johnson, N.; Sim, H.-S.; Fujiwara, A.; Kataoka, M. Picosecond coherent electron motion in a silicon single-electron source. arXiv 2019, arXiv:1903.07802. [Google Scholar]
- Kashcheyevs, V.; Kaestner, B. Universal Decay Cascade Model for Dynamic Quantum Dot Initialization. Phys. Rev. Lett. 2010, 104, 186805. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seo, M.; Ahn, Y.-H.; Oh, Y.; Chung, Y.; Ryu, S.; Sim, H.-S.; Lee, I.-H.; Bae, M.-H.; Kim, N. Improvement of electron pump accuracy by a potential-shape-tunable quantum dot pump. Phys. Rev. B 2014, 90, 085307. [Google Scholar] [CrossRef]
- Kataoka, M.; Fletcher, J.; See, P.; Giblin, S.P.; Janssen, T.J.B.M.; Griffiths, J.P.; Jones, G.A.C.; Farrer, I.; Ritchie, D.A. Tunable Nonadiabatic Excitation in a Single-Electron Quantum Dot. Phys. Rev. Lett. 2011, 106, 126801. [Google Scholar] [CrossRef] [PubMed]
- Roche, B.; Riwar, R.-P.; Voisin, B.; Dupont-Ferrier, E.; Wacquez, R.; Vinet, M.; Sanquer, M.; Splettstoesser, J.; Jehl, X. A two-atom electron pump. Nat. Commun. 2014, 4, 1581. [Google Scholar] [CrossRef] [PubMed]
- Yamahata, G.; Nishiguchi, K.; Fujiwara, A. Gigahertz single-trap electron pumps in silicon. Nat. Commun. 2014, 5, 5038. [Google Scholar] [CrossRef] [PubMed]
- Wenz, T.; Hohls, F.; Jehl, X.; Sanquer, M.; Barraud, S.; Klochan, J.; Barinovs, G.; Kashcheyevs, V. Dopant-controlled single-electron pumping through a metallic island. Appl. Phys. Lett. 2016, 108, 213107. [Google Scholar] [CrossRef] [Green Version]
- Yamahata, G.; Giblin, S.P.; Kataoka, M.; Karasawa, T.; Fujiwara, A. High-accuracy current generation in the nanoampere regime from a silicon single-trap electron pump. Sci. Rep. 2017, 7, 45137. [Google Scholar] [CrossRef]
- Clapera, P.; Klochan, J.; Lavieville, R.; Barraud, S.; Hutin, L.; Sanquer, M.; Vinet, M.; Cinins, A.; Barinovs, G.; Kashcheyevs, V.; et al. Design and operation of CMOS-compatible electron pumps fabricated with optical lithography. IEEE Electron Device Lett. 2017, 38, 414–417. [Google Scholar] [CrossRef]






© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tettamanzi, G.C. Unusual Quantum Transport Mechanisms in Silicon Nano-Devices. Entropy 2019, 21, 676. https://doi.org/10.3390/e21070676
Tettamanzi GC. Unusual Quantum Transport Mechanisms in Silicon Nano-Devices. Entropy. 2019; 21(7):676. https://doi.org/10.3390/e21070676
Chicago/Turabian StyleTettamanzi, Giuseppe Carlo. 2019. "Unusual Quantum Transport Mechanisms in Silicon Nano-Devices" Entropy 21, no. 7: 676. https://doi.org/10.3390/e21070676
APA StyleTettamanzi, G. C. (2019). Unusual Quantum Transport Mechanisms in Silicon Nano-Devices. Entropy, 21(7), 676. https://doi.org/10.3390/e21070676