On a Generalization of the Jensen–Shannon Divergence and the Jensen–Shannon Centroid
Abstract
:1. Introduction
- First, we generalize the Jensen–Bregman divergence by skewing a weighted separable Jensen–Bregman divergence with a k-dimensional vector in Section 2. This yields a generalization of the symmetric skew -Jensen–Shannon divergences to a vector-skew parameter. This extension retains the key properties for being upper-bounded and for application to densities with potentially different supports. The proposed generalization also allows one to grasp a better understanding of the “mechanism” of the Jensen–Shannon divergence itself. We also show how to directly obtain the weighted vector-skew Jensen–Shannon divergence from the decomposition of the KLD as the difference of the cross-entropy minus the entropy (i.e., KLD as the relative entropy).
- Second, we prove that weighted vector-skew Jensen–Shannon divergences are f-divergences (Theorem 1), and show how to build families of symmetric Jensen–Shannon-type divergences which can be controlled by a vector of parameters in Section 2.3, generalizing the work of [20] from scalar skewing to vector skewing. This may prove useful in applications by providing additional tuning parameters (which can be set, for example, by using cross-validation techniques).
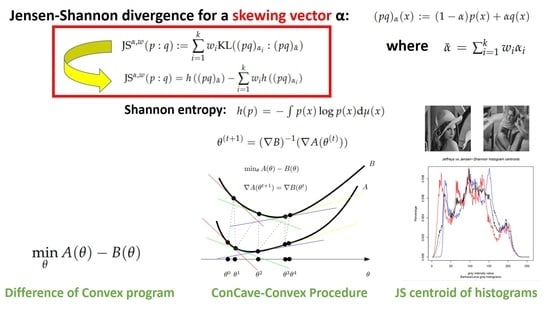
- Third, we consider the calculation of the Jensen–Shannon centroids in Section 3 for densities belonging to mixture families. Mixture families include the family of categorical distributions and the family of statistical mixtures sharing the same prescribed components. Mixture families are well-studied manifolds in information geometry [25]. We show how to compute the Jensen–Shannon centroid using a concave–convex numerical iterative optimization procedure [27]. The experimental results graphically compare the Jeffreys centroid with the Jensen–Shannon centroid for grey-valued image histograms.
2. Extending the Jensen–Shannon Divergence
2.1. Vector-Skew Jensen–Bregman Divergences and Jensen Diversities
2.2. Vector-Skew Jensen–Shannon Divergences
- and
- .
2.3. Building Symmetric Families of Vector-Skewed Jensen–Shannon Divergences
- Consider . Let denote the weight vector, and the skewing vector. We have . The vector-skew JSD is symmetric iff. (with ) and . In that case, we have , and we obtain the following family of symmetric Jensen–Shannon divergences:
- Consider , weight vector , and skewing vector for . Then, , and we get the following family of symmetric vector-skew JSDs:
- We can similarly carry on the construction of such symmetric JSDs by increasing the dimensionality of the skewing vector.
3. Jensen–Shannon Centroids on Mixture Families
3.1. Mixture Families and Jensen–Shannon Divergences
3.2. Jensen–Shannon Centroids
3.2.1. Jensen–Shannon Centroids of Categorical Distributions
| Algorithm 1: The CCCP algorithm for computing the Jensen–Shannon centroid of a set of categorical distributions. |
 |
3.2.2. Special Cases
- For the special case of , the categorical family is the Bernoulli family, and we have (binary negentropy), (and ) and . The CCCP update rule to compute the binary Jensen–Shannon centroid becomes
- Since the skew-vector Jensen–Shannon divergence formula holds for positive densities:we can relax the computation of the Jensen–Shannon centroid by considering 1D separable minimization problems. We then normalize the positive JS centroids to get an approximation of the probability JS centroids. This approach was also considered when dealing with the Jeffreys’ centroid [18]. In 1D, we have , and .
3.2.3. Some Remarks and Properties
4. Conclusions and Discussion
- It is always bounded,
- it applies to densities with potentially different supports, and
- it extends to unnormalized densities while enjoying the same formula expression.
Funding
Acknowledgments
Conflicts of Interest
References
- Billingsley, P. Probability and Measure; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Deza, M.M.; Deza, E. Encyclopedia of Distances; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Basseville, M. Divergence measures for statistical data processing—An annotated bibliography. Signal Process. 2013, 93, 621–633. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Nielsen, F. On the Jensen–Shannon Symmetrization of Distances Relying on Abstract Means. Entropy 2019, 21, 485. [Google Scholar] [CrossRef] [Green Version]
- Lin, J. Divergence measures based on the Shannon entropy. IEEE Trans. Inf. Theory 1991, 37, 145–151. [Google Scholar] [CrossRef] [Green Version]
- Sason, I. Tight bounds for symmetric divergence measures and a new inequality relating f-divergences. In Proceedings of the 2015 IEEE Information Theory Workshop (ITW), Jerusalem, Israel, 26 April–1 May 2015; pp. 1–5. [Google Scholar]
- Wong, A.K.; You, M. Entropy and distance of random graphs with application to structural pattern recognition. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 599–609. [Google Scholar] [CrossRef]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory 2003, 49, 1858–1860. [Google Scholar] [CrossRef] [Green Version]
- Kafka, P.; Österreicher, F.; Vincze, I. On powers of f-divergences defining a distance. Stud. Sci. Math. Hung. 1991, 26, 415–422. [Google Scholar]
- Fuglede, B. Spirals in Hilbert space: With an application in information theory. Expo. Math. 2005, 23, 23–45. [Google Scholar] [CrossRef] [Green Version]
- Acharyya, S.; Banerjee, A.; Boley, D. Bregman divergences and triangle inequality. In Proceedings of the 2013 SIAM International Conference on Data Mining, Austin, TX, USA, 2–4 May 2013; pp. 476–484. [Google Scholar]
- Naghshvar, M.; Javidi, T.; Wigger, M. Extrinsic Jensen–Shannon divergence: Applications to variable-length coding. IEEE Trans. Inf. Theory 2015, 61, 2148–2164. [Google Scholar] [CrossRef] [Green Version]
- Bigi, B. Using Kullback-Leibler distance for text categorization. In European Conference on Information Retrieval; Springer: Berlin/Heidelberg, Germany, 2003; pp. 305–319. [Google Scholar]
- Chatzisavvas, K.C.; Moustakidis, C.C.; Panos, C. Information entropy, information distances, and complexity in atoms. J. Chem. Phys. 2005, 123, 174111. [Google Scholar] [CrossRef] [Green Version]
- Yurdakul, B. Statistical Properties of Population Stability Index. Ph.D. Thesis, Western Michigan University, Kalamazoo, MI, USA, 2018. [Google Scholar]
- Jeffreys, H. An invariant form for the prior probability in estimation problems. Proc. R. Soc. Lond. A 1946, 186, 453–461. [Google Scholar]
- Nielsen, F. Jeffreys centroids: A closed-form expression for positive histograms and a guaranteed tight approximation for frequency histograms. IEEE Signal Process. Lett. 2013, 20, 657–660. [Google Scholar] [CrossRef] [Green Version]
- Lee, L. Measures of Distributional Similarity. In Proceedings of the 37th Annual Meeting of the Association for Computational Linguistics on Computational Linguistics, ACL ’99; Association for Computational Linguistics: Stroudsburg, PA, USA, 1999; pp. 25–32. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, F. A family of statistical symmetric divergences based on Jensen’s inequality. arXiv 2010, arXiv:1009.4004. [Google Scholar]
- Lee, L. On the effectiveness of the skew divergence for statistical language analysis. In Proceedings of the 8th International Workshop on Artificial Intelligence and Statistics (AISTATS 2001), Key West, FL, USA, 4–7 January 2001. [Google Scholar]
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observation. Stud. Sci. Math. Hung. 1967, 2, 229–318. [Google Scholar]
- Ali, S.M.; Silvey, S.D. A general class of coefficients of divergence of one distribution from another. J. R. Stat. Soc. Ser. B (Methodol.) 1966, 28, 131–142. [Google Scholar] [CrossRef]
- Sason, I. On f-divergences: Integral representations, local behavior, and inequalities. Entropy 2018, 20, 383. [Google Scholar] [CrossRef] [Green Version]
- Amari, S.I. Information Geometry and Its Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Jiao, J.; Courtade, T.A.; No, A.; Venkat, K.; Weissman, T. Information measures: The curious case of the binary alphabet. IEEE Trans. Inf. Theory 2014, 60, 7616–7626. [Google Scholar] [CrossRef]
- Yuille, A.L.; Rangarajan, A. The concave-convex procedure (CCCP). In Proceedings of the Neural Information Processing Systems 2002, Vancouver, BC, Canada, 9–14 December 2002; pp. 1033–1040. [Google Scholar]
- Nielsen, F.; Nock, R. Skew Jensen-Bregman Voronoi diagrams. In Transactions on Computational Science XIV; Springer: Berlin/Heidelberg, Germany, 2011; pp. 102–128. [Google Scholar]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749. [Google Scholar]
- Nielsen, F.; Nock, R. Sided and symmetrized Bregman centroids. IEEE Trans. Inf. Theory 2009, 55, 2882–2904. [Google Scholar] [CrossRef] [Green Version]
- Melbourne, J.; Talukdar, S.; Bhaban, S.; Madiman, M.; Salapaka, M.V. On the Entropy of Mixture distributions. Available online: http://box5779.temp.domains/~jamesmel/publications/ (accessed on 16 February 2020).
- Guntuboyina, A. Lower bounds for the minimax risk using f-divergences, and applications. IEEE Trans. Inf. Theory 2011, 57, 2386–2399. [Google Scholar] [CrossRef]
- Sason, I.; Verdu, S. f-divergence Inequalities. IEEE Trans. Inf. Theory 2016, 62, 5973–6006. [Google Scholar] [CrossRef]
- Melbourne, J.; Madiman, M.; Salapaka, M.V. Relationships between certain f-divergences. In Proceedings of the 57th Annual Allerton Conference on Communication, Control, and Computing (Allerton), Monticello, IL, USA , 24–27 September 2019; pp. 1068–1073. [Google Scholar]
- Sason, I. On Data-Processing and Majorization Inequalities for f-Divergences with Applications. Entropy 2019, 21, 1022. [Google Scholar] [CrossRef] [Green Version]
- Van Erven, T.; Harremos, P. Rényi divergence and Kullback-Leibler divergence. IEEE Trans. Inf. Theory 2014, 60, 3797–3820. [Google Scholar] [CrossRef] [Green Version]
- Xu, P.; Melbourne, J.; Madiman, M. Infinity-Rényi entropy power inequalities. In Proceedings of the 2017 IEEE International Symposium on Information Theory (ISIT), Aachen, Germany, 25–30 June 2017; pp. 2985–2989. [Google Scholar]
- Nielsen, F.; Nock, R. On the geometry of mixtures of prescribed distributions. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 2861–2865. [Google Scholar]
- Fréchet, M. Les éléments aléatoires de nature quelconque dans un espace distancié. Ann. De L’institut Henri PoincarÉ 1948, 10, 215–310. [Google Scholar]
- Nielsen, F.; Boltz, S. The Burbea-Rao and Bhattacharyya centroids. IEEE Trans. Inf. Theory 2011, 57, 5455–5466. [Google Scholar] [CrossRef] [Green Version]
- Lanckriet, G.R.; Sriperumbudur, B.K. On the convergence of the concave-convex procedure. In Proceedings of the Advances in Neural Information Processing Systems 22 (NIPS 2009), Vancouver, BC, Canada, 7–10 December 2009; pp. 1759–1767. [Google Scholar]
- Nielsen, F.; Sun, K. Guaranteed bounds on information-theoretic measures of univariate mixtures using piecewise log-sum-exp inequalities. Entropy 2016, 18, 442. [Google Scholar] [CrossRef] [Green Version]
- Springer Verlag GmbH, European Mathematical Society. Encyclopedia of Mathematics. Available online: https://www.encyclopediaofmath.org/ (accessed on 19 December 2019).
- Del Castillo, J. The singly truncated normal distribution: A non-steep exponential family. Ann. Inst. Stat. Math. 1994, 46, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, F.; Nock, R. Entropies and cross-entropies of exponential families. In Proceedings of the 2010 IEEE International Conference on Image Processing, Hong Kong, China, 26–29 September 2010; pp. 3621–3624. [Google Scholar]
- Nielsen, F.; Hadjeres, G. Monte Carlo information geometry: The dually flat case. arXiv 2018, arXiv:1803.07225. [Google Scholar]
- Schwander, O.; Nielsen, F. Learning mixtures by simplifying kernel density estimators. In Matrix Information Geometry; Springer: Berlin/Heidelberg, Germany, 2013; pp. 403–426. [Google Scholar]
- Arthur, D.; Vassilvitskii, S. k-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA’07), New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Nielsen, F.; Nock, R.; Amari, S.I. On clustering histograms with k-means by using mixed α-divergences. Entropy 2014, 16, 3273–3301. [Google Scholar] [CrossRef] [Green Version]
- Nielsen, F.; Nock, R. Total Jensen divergences: Definition, properties and clustering. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, QLD, Australia, 19–24 April 2015; pp. 2016–2020. [Google Scholar]
- Topsøe, F. Basic concepts, identities and inequalities-the toolkit of information theory. Entropy 2001, 3, 162–190. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial nets. In Proceedings of the Advances in Neural Information Processing Systems 27 (NIPS 2014), Montreal, QC, Canada, 8–13 December 2014; pp. 2672–2680. [Google Scholar]
- Yamano, T. Some bounds for skewed α-Jensen-Shannon divergence. Results Appl. Math. 2019, 3, 100064. [Google Scholar] [CrossRef]
- Kotlerman, L.; Dagan, I.; Szpektor, I.; Zhitomirsky-Geffet, M. Directional distributional similarity for lexical inference. Nat. Lang. Eng. 2010, 16, 359–389. [Google Scholar] [CrossRef]
- Johnson, D.; Sinanovic, S. Symmetrizing the Kullback-Leibler distance. IEEE Trans. Inf. Theory 2001, 1–8. [Google Scholar]




| Exponential Family | Mixture Family | |
|---|---|---|
| primal | ||
| dual | ||
| primal | ||
| Bregman divergence | ||
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nielsen, F. On a Generalization of the Jensen–Shannon Divergence and the Jensen–Shannon Centroid. Entropy 2020, 22, 221. https://doi.org/10.3390/e22020221
Nielsen F. On a Generalization of the Jensen–Shannon Divergence and the Jensen–Shannon Centroid. Entropy. 2020; 22(2):221. https://doi.org/10.3390/e22020221
Chicago/Turabian StyleNielsen, Frank. 2020. "On a Generalization of the Jensen–Shannon Divergence and the Jensen–Shannon Centroid" Entropy 22, no. 2: 221. https://doi.org/10.3390/e22020221
APA StyleNielsen, F. (2020). On a Generalization of the Jensen–Shannon Divergence and the Jensen–Shannon Centroid. Entropy, 22(2), 221. https://doi.org/10.3390/e22020221