Effect of Self-Oscillation on Escape Dynamics of Classical and Quantum Open Systems
Abstract
:1. Introduction
2. General Analysis of VAF: Damped Free Particle
3. Two Effects on Escape Dynamics of Classical and Quantum Open Systems
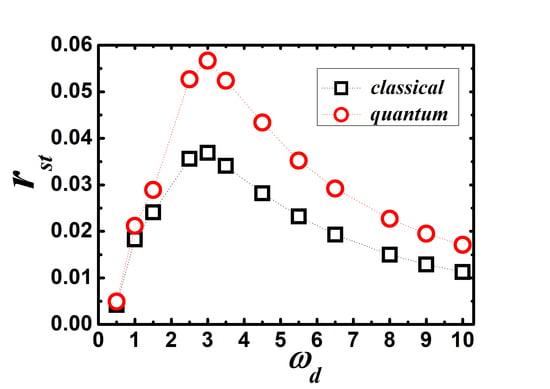
3.1. Effect of
3.2. Effect of N
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Einstein, A. Zur Theorie der Brownschen Bewegung. Ann. Phys. 1906, 19, 371–381. (In German) [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Eine neue Bestimmung der Moleküldimensionen. Ann. Phys. 1906, 19, 289–306. (In German) [Google Scholar] [CrossRef] [Green Version]
- Ness, H. Nonequilibrium Thermodynamics and Steady State Density Matrix for Quantum Open Systems. Entropy 2017, 19, 158. [Google Scholar] [CrossRef] [Green Version]
- Hatano, N.; Ordonez, G. Time-Reversal Symmetry and Arrow of Time in Quantum Mechanics of Open Systems. Entropy 2019, 21, 380. [Google Scholar] [CrossRef] [Green Version]
- Tsekov, R.; Ruckenstein, E. Stochastic dynamics of a subsystem interacting with a solid body with application to diffusive processes in solids. J. Chem. Phys. 1994, 100, 1450. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Influence of Dissipation on Quantum Tunneling in Macroscopic Systems. Phys. Rev. Lett. 1981, 46, 211–214. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Quantum Tunnelling in a Dissipative System. Ann. Phys. 1983, 149, 374–456. [Google Scholar] [CrossRef]
- Caldeira, A.O.; Leggett, A.J. Path Integral Approach to Quantum Brownian Motion. Physica A 1983, 121, 587–616. [Google Scholar] [CrossRef]
- Smith, S.T.; Onofri, R. Thermalization in open classical systems with finite heat baths. Eur. Phys. J. B 2008, 61, 271. [Google Scholar] [CrossRef]
- Hänggi, P.; Ingold, G.-L.; Talkner, P. Finite quantum dissipation: The challenge of obtaining specific heat. New J. Phys. 2008, 10, 115008. [Google Scholar] [CrossRef] [Green Version]
- Ingold, G.-L.; Hänggi, P.; Talker, P. Specific heat anomalies of open quantum systems. Phys. Rev. E 2009, 79, 061105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, Q.; Smith, S.T.; Onofrio, R. Equilibrium states of a test particle coupled to finite-size heat baths. Phys. Rev. E 2009, 79, 031128. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosa, J.; Beims, M.W. Dissipation and transport dynamics in a ratchet coupled to a discrete bath. Phys. Rev. E 2008, 78, 031126. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Spagnolo, B.; Guarcello, C.; Magazzù, L.; Carollo, A.; Persano, A.D.; Valenti, D. Nonlinear Relaxation Phenomena in Metastable Condensed Matter Systems. Entropy 2016, 19, 20. [Google Scholar] [CrossRef] [Green Version]
- Gerald, W.; Fixman, M. Diffusion-controlled intrachain reactions of polymers. I Theory. J. Chem. Phys. 1973, 60, 866. [Google Scholar]
- Szabo, A.; Schulten, K.; Schulten, Z. First passage time approach to diffusion controlled reactions. J. Chem. Phys. 1980, 72, 4350. [Google Scholar] [CrossRef]
- Verechtchaguina, T.; Sokolov, I.M.; Schimansky-Geier, L. First passage time densities in resonate-and-fire models. Phys. Rev. E 2006, 73, 031108. [Google Scholar] [CrossRef] [Green Version]
- Kramers, H.A. Brownian Motion in a Field of Force and the Diffusion Model of Chemical Reactions. Physica 1940, 7, 284. [Google Scholar] [CrossRef]
- Stella, L.; Lorenz, C.D.; Kantorovich, L. Generalized Langevin equation: An efficient approach to nonequilibrium molecular dynamics of open systems. Phys. Rev. B 2014, 89, 134303. [Google Scholar] [CrossRef] [Green Version]
- Bao, J.D. Generalized Einstein relations and conditions for anomalous relaxation. Phys. Rev. E 2019, 100, 052149. [Google Scholar] [CrossRef]
- Bao, J.D.; Zhuo, Y.Z.; Oliveira, F.A.; Hänggi, P. Intermediate dynamics between Newton and Langevin. Phys. Rev. E 2006, 74, 061111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qiu, Q.; Shi, X.Y.; Bao, J.D. Mixed nonergodicity of a forced system and its non-stationary strength. Europhys. Lett. 2019, 128, 20005. [Google Scholar] [CrossRef]
- Dhar, A.; Wagh, K. Equilibration problem for the generalized Langevin equation. Europhys. Lett. 2007, 79, 60003. [Google Scholar] [CrossRef]
- Ishikawa, F.; Todo, S. Localized mode and nonergodicity of a harmonic oscillator chain. Phys. Rev. E 2018, 98, 062140. [Google Scholar] [CrossRef] [Green Version]
- Ghosh, P.; Shit, A.; Chattopadhyay, S.; Chaudhuri, J.R. Escape of a driven particle from a metastable: A semiclassical approach. J. Chem. Phys. 2010, 132, 244506. [Google Scholar] [CrossRef]
- Banik, S.K.; Bag, B.C.; Ray, D.S. Generalized quantum Fokker-Planck, diffusion, and Smoluchowski equations with true probability distribution functions. Phys. Rev. E 2002, 65, 051106. [Google Scholar] [CrossRef] [Green Version]
- Zwanzig, R. Nonlinear Generalized Langevin Equations. J. Stat. Phys. 1973, 9, 3. [Google Scholar] [CrossRef]
- Hänggi, P.; Talkner, P.; Borkovec, M. Reaction-rate theory: Fifty years after Kramers. Rev. Mod. Phys. 1990, 62, 251–341. [Google Scholar] [CrossRef]
- Martens, C.C. Qualitative dynamics of generalized Langevin equations and the theory of chemical reaction rates. J. Chem. Phys. 2002, 116, 2516. [Google Scholar] [CrossRef]
- Ford, G.W.; Kac, M. On the Quantum Langevin Equation. J. Stat. Phys. 1987, 46, 803. [Google Scholar] [CrossRef]
- Bao, J.D. Non-Markovian Two-Time Correlation Dynamics and Nonergodicity. J. Stat. Phys. 2017, 168, 561–572. [Google Scholar] [CrossRef]
- Schiff, J.L. Complex Inversion Formula. In The Laplace Transform: Theory and Applications; Springer: New York, NY, USA, 1999; pp. 152–174. [Google Scholar]
- Lapas, L.C.; Morgado, R.; Vainstein, M.H.; Rubi, J.M.; Oliveira, F.A. Khinchin theorem and anomalous diffusion. Phys. Rev. Lett. 2008, 101, 230602. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Honeycutt, R.L. Stochastic Runge-Kutta algorithms. I. White noise. Phys. Rev. A 1992, 45, 600–603. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.D.; Wang, H.Y.; Jia, Y.; Zhuo, Y.Z. Cancellation phenomenon of barrier escape driven by a non-Gaussian noise. Phys. Rev. E 2005, 72, 051105. [Google Scholar] [CrossRef] [PubMed]
- Arrayás, M.; Kaufman, I.K.; Luchinsky, D.G.; McClintock, P.V.E.; Soskin, S.M. Kramers Problem for a Multiwell Potential. Phys. Rev. Lett. 2000, 84, 2556. [Google Scholar]
- Bao, J.D.; Jia, Y. Determination of fission rate by mean last passage time. Phys. Rev. C 2004, 69, 027602. [Google Scholar] [CrossRef]
- Sagnella, D.E.; Straub, J.E.; Thirumalai, D. Time scales and pathways for kinetic energy relaxation in solvated. J. Chem. Phys. 2000, 113, 17. [Google Scholar] [CrossRef] [Green Version]
- Hänggi, P. Memory effect on thermally activated escape rates. Phys. Rev. A 1982, 26, 2996–2999. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Bao, J. Effect of Self-Oscillation on Escape Dynamics of Classical and Quantum Open Systems. Entropy 2020, 22, 839. https://doi.org/10.3390/e22080839
Li M, Bao J. Effect of Self-Oscillation on Escape Dynamics of Classical and Quantum Open Systems. Entropy. 2020; 22(8):839. https://doi.org/10.3390/e22080839
Chicago/Turabian StyleLi, Minggen, and Jingdong Bao. 2020. "Effect of Self-Oscillation on Escape Dynamics of Classical and Quantum Open Systems" Entropy 22, no. 8: 839. https://doi.org/10.3390/e22080839
APA StyleLi, M., & Bao, J. (2020). Effect of Self-Oscillation on Escape Dynamics of Classical and Quantum Open Systems. Entropy, 22(8), 839. https://doi.org/10.3390/e22080839