Theoretical Reactivity Study of Indol-4-Ones and Their Correlation with Antifungal Activity

Abstract

Chemical reactivity descriptors of indol-4-ones obtained via density functional theory (DFT) and hard–soft acid–base (HSAB) principle were calculated to prove their contribution in antifungal activity. Simple linear regression was made for global and local reactivity indexes. Results with global descriptors showed a strong relationship between antifungal activity vs. softness (S) (r = 0.98) for series I (6, 7a–g), and for series II (8a–g) vs. chemical potential (µ), electronegativity (χ) and electrophilicity (ω) (r = 0.86), p < 0.05. Condensed reactivity descriptors s_k⁺, ω_k⁻ for different fragments had strong relationships for series I and II (r = 0.98 and r = 0.92). Multiple linear regression was statistically significant for S (r = 0.98), η (r = 0.91), and µ/ω (r = 0.91) in series I. Molecular electrostatic potential maps (MEP) showed negative charge accumulation around oxygen of carbonyl group and positive accumulation around nitrogen. Fukui function isosurfaces showed that carbons around nitrogen are susceptible to electrophilic attack, whereas the carbon atoms of the carbonyl and phenyl groups are susceptible to nucleophilic attack for both series. The above suggest that global softness in conjunction with softness and electrophilicity of molecular fragments in enaminone systems and pyrrole rings contribute to antifungal activity of indol-4-ones.

1. Introduction

Azole antifungal compounds have been used as therapeutic options for the treatment of systemic fungal infections. Mostly triazoles (fluconazole, etc.) and imidazoles (ketoconazole, etc.) [1,2] are used effectively against yeast and filamentous fungi. However, some etiologic agents have developed resistance by different mechanisms; moreover, azole compounds also present toxicity or side effects [2,3,4,5]. Consequently, some studies to discover new antifungal agents have been done [3,6].

Recently, González et al. designed and synthesized a series of novel indol-4-one derivatives with 1- and 2-(2,4-substituted phenyl) side chains (Figure 1). These compounds were tested in vitro against eight human pathogenic filamentous fungus and yeast strains by determination of the minimal inhibitory concentration (MIC); as MIC decreased, the antifungal activity increased. Based on their results, they reported activity against Candida tropicalis, Candida guilliermondii and Candida parapsilosis at MIC values of 0.0316 mM (8 µg·mL⁻¹) for compounds 8a–g; and MIC values of 0.1014 mM (31.25 µg·mL⁻¹) against Aspergillus fumigatus (

Table 1. MIC in vitro of 6, 7a–g and 8a–g against yeast and filamentous fungus.

Compound	X	C. albicans		C. glabrata		C. krusei		C. tropicalis		C. guilliermondii		C. parapsilosis		A. niger		A. fumigatus
		24 h	48 h	24 h	48 h	24 h	48 h	24 h	48 h	24 h	48 h	24 h	48 h	48h h	72 h	48 h	72 h
6		1.4105	2.8210	2.8210	5.6420	2.8210	5.6420	1.4105	5.6420	1.4105	2.8210	0.0451	0.3526	0.7052	1.4105	0.7052	1.4105
7a	H	0.2467	1.9736	0.9868	3.9473	0.9868	3.9473	0.4934	3.9473	0.4934	0.4934	0.0316	0.2467	0.2467	0.4934	0.2467	0.4934
7b	2-F	0.2304	1.8428	0.4607	3.6856	0.9214	3.6856	0.4607	3.6856	0.4607	0.4607	0.0590	0.2304	0.2304	0.2304	0.1152	0.4607
7c	4-F	0.2304	1.8428	0.4607	3.6856	0.9214	3.6856	0.4607	3.6856	0.4607	0.4607	0.0590	0.9214	0.4607	0.9214	0.2304	0.9214
7d	2,4-diF	0.4321	0.8641	0.8641	3.4564	0.4321	0.8641	0.2160	0.4321	0.4321	0.4321	0.0553	0.2160	0.2160	0.4321	0.4321	0.8641
7e	2-Cl	0.4344	0.8687	0.8687	3.4748	0.4344	0.8687	0.2172	0.4344	0.4344	0.4344	0.1086	0.1086	0.2172	0.8687	0.1086	0.4344
7f	4-Cl	0.4344	0.8687	0.8687	3.4748	0.4344	0.8687	0.2172	0.4344	0.4344	0.4344	0.0556	0.2154	0.4344	>0.8687	0.4344	0.8687
7g	2,4-diCl	0.3879	0.7758	0.7758	3.1034	0.3879	0.7758	0.1940	0.3879	0.3879	0.3879	0.0970	0.7758	>0.7758	>0.7758	0.3879	0.3879
8a	H	0.5223	1.0447	0.5223	4.1787	0.5223	1.0445	0.2612	0.5223	0.2612	0.5223	0.0669	1.0447	>1.0447	>1.0447	1.0447	1.0447
8b	2-F	0.4858	0.9716	0.4858	0.9716	0.4858	0.9716	0.2429	0.4858	0.2429	0.2429	0.0622	0.2410	>0.9716	>0.9716	0.9716	0.9716
8c	4-F	0.2429	0.9716	0.4858	0.9716	0.2429	0.4858	0.1214	0.2429	0.1214	0.2429	0.0622	0.2410	>0.9716	>0.9716	>0.9716	>0.9716
8d	2,4-diF	0.2270	0.9081	0.4541	0.9081	0.2270	0.4541	0.1135	0.2270	0.1135	0.2270	0.0581	0.9081	>0.9081	>0.9081	>0.9081	>0.9081
8e	2-Cl	0.2283	0.9132	0.4566	0.9132	0.2283	0.4566	0.1142	0.2283	0.1142	0.1142	0.1142	0.9132	>0.9132	>0.9132	>0.9132	>0.9132
8f	4-Cl	0.2283	0.9132	0.4566	0.9132	0.2283	0.4566	0.1142	0.2283	0.1142	0.1142	0.0584	0.2265	>0.9132	>0.9132	>0.9132	>0.9132
8g	2,4-diCl	0.2028	0.8112	0.4056	0.8112	0.2028	0.4056	0.1014	0.1014	0.1014	0.1014	0.1014	0.2012	>0.8112	>0.8112	>0.8112	>0.8112

This table was modified and taken from González et al. paper [6], the MIC values were changed from µg·mL⁻¹ to mM.

) for compounds 7a–g. A change in the position of the halophenyl regioisomers from N-1 to C-2 increased the antifungal activity. It was the first report about antifungal activity for these indol-4-one derivatives.

Density functional theory (DFT) and the hard–soft acid–base principle (HSAB) have been used to study the biological activity of some biomolecules. Fukui functions were used for understanding the reactivity of nitrogenous bases of DNA and RNA [7,8]; chemical hardness was used to study the dopamine drug–receptor interactions [9]; the relationship between different biological activity and chemical reactivity indices, such as electrophilicity, hardness, and electronegativity was used for testosterone derivatives and their biological activity [10,11]; the dipolar moment, ionization potential, electronic affinity, electronegativity, electrophilicity, and others showed the inhibitory activity of carbonic anhydrase [12]; quantum chemical descriptors were used to study protoporphyrinogen oxidase inhibitors [13,14]; Fukui functions, softness, and electrostatic potential were useful for an antituberculotic drug design [15]; hardness, electronegativity, softness and electrophilicity has been applied to study the toxicity in specific species [16]; different descriptors were used to study mosquito repellent [17]; parameters such as dipolar moment were used to study chemical radioactivity protector [18]; ionization potential and charge were used to study antioxidants [19]; other activities and chemical reactivity parameters have been used in the study of nonnucleoside HIV-1 reverse transcriptase inhibitors [20], histone deacetylase inhibitors [21], and anti-HIV-1 integrase [22]; anti-HIV activity vs. electronegativity, hardness, chemical power, and electrophilicity was evaluated [23,24]; and others [25,26]. Within the above lies the importance of understanding the biological activity in a particular molecular set [27] and therefore for rational drug design.

In this work we made a DFT-HSAB reactivity study of the indol-4-one derivatives 6–8 to understand which molecular fragments are essential for antifungal activity. The development of new antifungal drugs can be based on obtaining good relationships between DFT-HSAB reactivity descriptors and antifungal activity. Based on the biological activity results reported by González et al. [6], we classified the indol-4-one derivatives 6–8 into two series according to the structure and biological activity. Series I includes compounds 6 and 7a–g, while series II includes compounds 8a–g.

2. Theoretical Methods

The geometries of the molecules 6, 7a–g and 8a–g (Figure 1) were fully optimized at the B3LYP/6-311+G (d,p) level of theory using the Gaussian 09 program package [28]. For all stationary points, vibrational analyses were carried out. The ionization potential I = E_N−1 − E_N and the electronic affinity A = E_N − E_{N + 1} were calculated at the geometry of the neutral species using the respective vertical energies E_N, E_{N + 1}, and E_{N − 1} of the systems with N, N + 1 and N − 1 electrons. The global reactivity indexes, chemical potential $\mu =-\frac{1}{2}\left(I+A\right)$, electronegativity $\chi =-\mathsf{\mu }$, hardness $\eta =\frac{1}{2}\left(I-A\right)$, softness $S=1/\eta$ and electrophilicity $\omega =\frac{{\chi }^2}{2\eta }$ [29,30,31], were calculated.

The local Fukui functions for nucleophilic $f^{+}\left(\mathit{r}\right)$, electrophilic $f^{-}\left(\mathit{r}\right)$, and radical $f^0\left(\mathit{r}\right)$ attacks were calculated using Equations (1)–(3) [32].

$$f^{+}\left(\mathit{r}\right)={\rho }_{N+1}\left(\mathit{r}\right)-{\rho }_N\left(\mathit{r}\right)\mathrm{Nucleophilic}\mathrm{attack}$$

(1)

$$f^{-}\left(\mathit{r}\right)={\rho }_N\left(\mathit{r}\right)-{\rho }_{N-1}\left(\mathit{r}\right)\mathrm{Electrophilic}\mathrm{attack}$$

(2)

$$f^0\left(\mathit{r}\right)=\frac{1}{2}\left[{\rho }_{N+1}\left(\mathit{r}\right)-{\rho }_{N-1}\left(\mathit{r}\right)\right]\mathrm{Radical}\mathrm{attack}$$

(3)

where ${\rho }_{N+1}\left(\mathit{r}\right)$, ${\rho }_N\left(\mathit{r}\right)$ and ${\rho }_{N-1}\left(\mathit{r}\right)$ are the electronic densities for the systems with N + 1, N and N − 1 electrons, respectively, calculated with the geometry of the neutral species.

The condensed Fukui functions were calculated using the charge of each atom $q_k$ instead of the electron density $\rho \left(\mathit{r}\right)$ (Equations (4)–(6)) [32,33,34,35]. The Hirshfeld population analysis scheme was used for the systems with N, N − 1 and N + 1 number of electrons. The condensed softness $s_k^{+}=S{f}_k^{+}$, $s_k^{\mathrm{o}}=S{f}_k^{\mathrm{o}}$ and $s_k^{-}=S{f}_k^{-}$ and condensed electrophilicity indexes ${\mathsf{\omega }}_k^{+}=S{\mathsf{\omega }}_k^{+}$, ${\mathsf{\omega }}_k^{\mathrm{o}}=\mathsf{\omega }{f}_k^{\mathrm{o}}$, ${\mathsf{\omega }}_k^{-}=\mathsf{\omega }{f}_k^{-}$ were obtained. The local Fukui function isosurfaces were plotted with GaussView 5.0 [36].

Condensed Fukui functions:

$$f_k^{+}=q_k\left(N+1\right)-q_k\left(N\right)\mathrm{Nucleophilic}\mathrm{attack}$$

(4)

$$f_k^{-}=q_k\left(N\right)-q_k\left(N-1\right)\mathrm{Electrophilic}\mathrm{attack}$$

(5)

$$f_k^0=\frac{1}{2}(q_k\left(N+1\right)-q_k\left(N-1\right))\mathrm{Radical}\mathrm{attack}$$

(6)

where $q_k$ is the electronic population value of k^th atom in the molecule.

3. Structure-Activity Relationship (SAR) Statistical Procedure

A simple and multiple regression analysis were made for the antifungal activities and the global and condensed reactivity indexes for each series of compounds. The Pearson and Determination Coefficients were obtained using SAS software [37] considering p < 0.05 as a significant value; the analysis was made for each time of testing: 24 and 48 h for yeast; and 48 and 72 h for filamentous fungus.

4. Results and Discussion

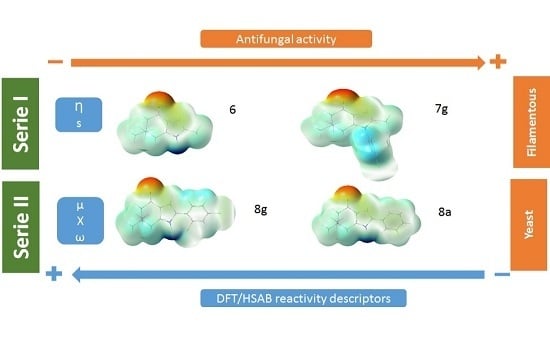
4.1. Global Reactivity Parameters

Table 2. Global reactivity descriptors for the 15 compounds indol-4-ones 6, 7a–g and 8a–g.

Compound	η (eV)	χ (eV)	ω (eV)
6	4.18	3.63	1.58
7a	3.92	3.65	1.70
7b	3.89	3.74	1.80
7c	3.91	3.77	1.82
7d	3.91	3.81	1.86
7e	3.89	3.71	1.76
7f	3.85	3.84	1.92
7g	3.80	3.90	2.00
8a	3.82	3.57	1.67
8b	3.80	3.67	1.77
8c	3.84	3.64	1.72
8d	3.74	3.77	1.90
8e	3.78	3.73	1.84
8f	3.73	3.72	1.85
8g	3.74	3.87	2.01

shows the values of the calculated global chemical reactivity parameters for the 15 indol-4-ones compounds. The chemical reactivity values vary with the molecular structure and the substituent. According to the structural homology, the analyzed compounds were divided into two series: series I that includes compounds 6 and 7a–g (N-1 substitution with phenyl moieties) and series II that includes compounds 8a to 8g (C-2 substitution with phenyl moieties). Table 2 shows that for series I compound 6 has the highest hardness value (4.18 eV) and 7g has the lowest hardness value (3.80 eV); the difference is 0.38 eV. In contrast, for series II the highest hardness value (3.84 eV) corresponds to compound 8c and the lowest value (3.73 eV) to 8f and the difference is 0.11 eV. According to the maximum hardness principle, compounds 7g and 8f (8g and 8d also) are more reactive than 6 and 8c, respectively. The electronegativity equalization principle assures in the course of a chemical reaction energetic stabilization through equalization of middle HOMO-LUMO levels among ligand and receptor active molecular structures [38]. Table 2 reflects that compounds 7g in series I and 8g in series II present the highest electronegativity values (3.90 eV and 3.87 eV, respectively). The electrophilicity index ω value for the same compounds (7g 2.00 eV and 8g 2.01 eV), reflects the ability of 7g and 8g to behave as the stronger electrophiles on each series. The relative change between the maximum and minimum values of ω in the Series I of Table 2 (ω_max − ω_min/ω_max) = 0.21 is larger than the corresponding change of 0.17 for series II. This indicates that the capacity of series I to accept electrons (electrophilic character) is more sensitive to the specific substituent than series II.

Simple linear regression of the minimum inhibitory concentration (MIC) vs. global reactivity parameters for both series was obtained (

Table 3. Pearson coefficient for each simple lineal regression for series I: Compounds 6 and 7a–g.

Microorganism	Time of Testing (h)	η (eV)		χ (eV)		ω (eV)
		r	p	r	p	r	p
C. albicans	24	0.87	0.0048	0.43	0.2868	0.60	0.1124
	48	0.82	0.0128	0.77	0.0246	0.83	0.0099
C. glabrata	24	0.90	0.0022	0.55	0.1602	0.70	0.0550
	48	0.98	0.00002	0.74	0.0358	0.86	0.0055
C. krusei	24	0.95	0.0003	0.69	0.0572	0.82	0.0126
	48	0.76	0.0283	0.75	0.0302	0.80	0.0166
C. tropicalis	24	0.95	0.0003	0.69	0.0572	0.82	0.0126
	48	0.74	0.0363	0.75	0.0331	0.79	0.0199
C. guilliermondii	24	0.96	0.0002	0.61	0.1109	0.76	0.0285
	48	0.94	0.0004	0.57	0.1393	0.73	0.0396
C. parapsilosis	24	0.46	0.2571	0.41	0.3145	0.46	0.2544
	48	0.15	0.7242	0.39	0.3419	0.33	0.4221
A. niger	48	0.75	0.0500	0.25	0.5875	0.47	0.2899
	72	0.78	0.0650	0.49	0.3236	0.68	0.1398
A. fumigatus	48	0.61	0.1062	0.01	0.9797	0.22	0.6061
	72	0.79	0.0191	0.29	0.4893	0.49	0.2188

h = hours, η = hardness, χ = electronegativity, and ω = electrophilicity index. In gray color is indicated the values that are statically significant p < 0.05.

and

Table 4. Pearson coefficient for simple lineal regression for series II: Compounds 8a–g.

Microorganism	Time of Testing (h)	η (eV)		χ (eV)		ω (eV)
		r	p	r	p	r	p
C. albicans	24	0.54	0.2155	0.71	0.0731	0.70	0.0821
	48	0.78	0.0406	0.98	0.00006	0.98	0.0002
C. glabrata	24	0.78	0.0406	0.98	0.00006	0.98	0.0002
	48	0.44	0.3173	0.66	0.1060	0.63	0.1285
C. krusei	24	0.54	0.2155	0.71	0.0731	0.70	0.0821
	48	0.54	0.2155	0.71	0.0731	0.70	0.0821
C. tropicalis	24	0.54	0.2155	0.71	0.0731	0.70	0.0821
	48	0.58	0.1673	0.82	0.0250	0.80	0.0315
C. guilliermondii	24	0.54	0.2155	0.71	0.0731	0.70	0.0821
	48	0.61	0.1488	0.78	0.0400	0.76	0.0472
C. parapsilosis	24	0.14	0.7712	0.49	0.2594	0.44	0.3164
	48	0.13	0.7774	0.27	0.5546	0.2547	0.5814

h = hours, η = hardness, χ = electronegativity, and ω = electrophilicity index. In gray color is indicated the values that are statically significant p < 0.05.

). The Pearson coefficient was positive and the relationships were directly proportional: when the antifungal activity decreased, the global reactivity values increased. Then, when the global reactivity of those 15 indol-4-ones decreases, the higher antifungal activity is obtained. The best statistically significant relationships (the Pearson coefficient p < 0.05) between both variables were obtained for yeast in series I: global hardness for C. glabrata 48 h (r_η = 0.98), C. krusei 24 h (r_η = 0.95), C. tropicalis 24 h (r_η = 0.95), C. guilliermondii 24 (r_η = 0.96) and 48 h (r_η = 0.94), and fungi: A. fumigatus 72 h (r_η = 0.79) (Table 3. This means a strong linear relationship between hardness and biological activity (96%, r² values until 0.96), with only 4% of variance of activity left to explain after taking into account the hardness in a linear way. For series II, global electronegativity and global electrophilicity index had a higher Pearson coefficient for C. albicans 48 h and C. glabrata 24 h (r_χ,ω = 0.98) and C. tropicalis 48 h (r_χ = 0.82 and r_ω = 0.80) (Table 4). This shows the same tendency as series I, with electronegativity and electrophilicity.

The relationship was strong for almost all cases, except for C. parapsilosis where the relationship did not have statistical significance.

Pearson coefficient in simple linear regression for series I had the following hierarchy from higher to lower values: η > ω > χ while χ = ω > η for series II. This could be related to results obtained by Putz et al. [24], where they report values of monolinear correlation of activity of uracil derivatives (anti-HIV action) vs. chemical reactivity indices, and the tendency shown was η > ω > χ, which is not the tendency one may expect obeying the established hierarchy for chemical binding scenario given by Putz [39], according which a chemical reaction/interaction is triggered by the electronegativity difference, followed by chemical hardness and electrophilicity: χ > η > ω, due to chemical–biological interactions. The higher Pearson coefficient presented by Putz is 0.67 for hardness, lower than the calculated value of the same parameter, 0.98. Although a different pharmacological activity is evaluated, it is possible to see the relation that can exist with these electronic properties of systems.

Stachowicz et al. evaluated thioamides derivatives and their activity against C. albicans and correlated their activity vs. hardness, softness, and electrophilicity, with r values around 0.72 to 0.93 [40]. These results coincide with those obtained by us with r values around 0.73 to 0.98; the chemical structure for thioamides are similar to indol-4-ones, =only in the presence of N-heterocyclic system of five members, and this similarity could be responsible for similar correlations between biological activities and chemical reactivity parameters.

Different biological activities have been correlated with chemical reactivity parameters: hardness, softness, chemical potential, electronegativity, electrophilicity, and other electronic parameters looking for any relationship between electronic parameters and biological activity. Examples of studies with different parameters are: for testosterone derivatives r_ω = 0.42–0.94 [10,11]; carbonic anhydrase inhibitory r_{χ,µ,S,εLUMO} = 0.92 [12]; anti HIV-1 integrase r_LogP,χ = 0.93 [22]; anti-HIV activity with uracil derivatives r_χ = 0.24, r_η = 0.65, r_ω = 0.65, r_ω,χ = 0.69, and r_ω,η = 0.68, [24]; etc. Although our analysis of antifungal activity does not match with those described above, the obtained values of r are better.

Multiple lineal regression for global reactivity indexes indicated that both hardness and softness are significant variables for series I (see

Table 5. Multiple regression analysis for series I: Compounds 6 and 7a–g.

Microorganism	Time of Testing (h)	r	r2	p	Significant Indexes
C. albicans	24	0.97	0.94	0.00070	η, S
	48	0.83	0.70	0.01000	ω
C. glabrata	24	0.97	0.94	0.00100	η, S
	48	0.98	0.96	<0.0001	η
C. krusei	24	0.95	0.91	0.00030	η
	48	0.80	0.64	0.01660	ω
C. tropicalis	24	0.95	0.91	0.00030	η
	48	0.79	0.62	0.02000	ω
C. guilliermondii	24	0.99	0.99	<0.0001	η, S
	48	0.99	0.99	<0.0001	η, S
C. parapsilosis	24	0.72	0.51	0.60230	No variable
	48	0.49	0.24	0.89800	No variable
A. niger	48	0.75	0.57	0.05070	η
	72	0.78	0.61	0.06480	η
A. fumigatus	48	0.91	0.84	0.01080	η, ω
	72	0.91	0.83	0.01140	η, µ

). The relationship was strong for C. guilliermondii 24 h (r = 0.99) and 48 h (r = 0.99). Hardness and electrophilicity as well as hardness and chemical potential had strong relationship for fungi, and are indicated specifically for A. fumigatus 48 h (r_η,s = 0.91) and 72 h (r_η,µ = 0.91). For series II, there is no statistically significance (p > 0.05) linking two or more descriptors.

4.2. Local and Fragment Reactivity Parameters

The local Fukui function is related with the frontier controlled soft–soft interactions. Figure 2 shows the isosurface plot of the Fukui function for an electrophilic attack $f^{-}\left(\mathit{r}\right)$, and the positive values are shown in purple. For series I, the carbon atoms neighboring the nitrogen atom of the pyrrole ring are susceptible to be attacked by a soft electrophile followed by the oxygen atom of the carbonyl group and the vinylic carbon atoms of the pirrolic ring. For compounds in series II, the Fukui function shows the same reactive sites than series I. In addition, the carbon atom in the para-position of the phenyl ring is susceptible for electrophilic attack.

Figure 3 shows the Fukui function for nucleophilic attack $f^{+}\left(\mathit{r}\right)$, and the regions in purple color are positive values and show the most favorable sites for the attack of a soft nucleophile. For series I, the carbonyl and phenyl carbon atoms are prone to nucleophilic attack. For series II, these regions are the carbonyl group and carbon atoms from vinyl and phenyl ring.

The local Fukui function is localized within the carbonyl, pyrrole and phenyl moieties. In order to understand which molecular fragments are responsible for antifungal activity, the softness and electrophilicity were calculated for different fragments of compounds 6, 7a–g and 8a–g.

Table 6. Chemical reactivity criterions by fragment for series I (fragment ID: a–i) and series II (fragment ID: j–z).

ID	Microorganism	Time of Testing (h)	Fragment Chemical Parameter	r	Atoms Considered in the Fragment (Marked in Orange)
a	Aspergillus fumigatus	48	sk+	0.81
			ωk+	0.77
b	Aspergillus fumigatus	48	sk+	0.83
			ωk+	0.79
c	Aspergillus niger	72	sk+	0.98
			ωk+	0.89
d	Aspergillus niger	72	sk+	0.95
			ωk+	0.91
e	Aspergillus niger	72	sk+	0.88
f	Aspergillus niger	48	sk−	0.93
		72	sk−	0.85
	Aspergillus fumigatus	48	sk−	0.75
g	Aspergillus niger	48	sk−	0.90
		72	sk−	0.83
	Aspergillus fumigatus	48	sk−	0.74
h	Aspergillus fumigatus	48	sk0	0.82
			ωk0	0.72
i	Aspergillus fumigatus	48	sk0	0.80
j	Candida albicans	48	ωk+	0.75
	Candida glabrata	24		0.75
k	Candida albicans	48	ωk+	0.75
	Candida glabrata	24		0.75
l	Candida albicans	48	ωk+	0.75
	Candida glabrata	24		0.75
m	Candida albicans	48	ωk−	0.92
	Candida glabrata	24	ωk−	0.92
	Candida parapsilosis	24	sk−	0.78
n	Candida albicans	48	ωk−	0.92
	Candida glabrata	24	ωk−	0.92
	Candida parapsilosis	24	sk−	0.77
o	Candida albicans	48	sk−	0.83
	Candida glabrata	24		0.83
	Candida tropicalis	48		0.77
p	Candida parapsilosis	24	sk−	0.76
			ωk−	0.76
q	Candida albicans	48	ωk−	0.86
	Candida glabrata	24		0.86
r	Candida albicans	48	sk−	0.80
	Candida glabrata	24		0.80
s	Candida albicans	48	sk−	0.76
	Candida glabrata	24		0.76
t	Candida albicans	48	sk−	0.79
	Candida glabrata	24		0.79
u	Candida albicans	48	ωk−	0.86
	Candida glabrata	24		0.86
v	Candida albicans	48	sk−	0.79
	Candida glabrata	24		0.79
w	Candida albicans	48	ωk−	0.86
	Candida glabrata	24		0.86
x	Candida albicans	48	ωk−	0.83
	Candida glabrata	24		0.83
y	Candida albicans	48	sk−	0.76
	Candida glabrata	24		0.76
z	Candida albicans	24	ωk0	0.78
	Candida krusei	24	ωk0	0.78
		48	ωk0	0.78
	Candida tropicalis	24	ωk0	0.78
		48	ωk0	0.76
	Candida guilliermondii	24	ωk0	0.78
	Candidad parapsilosis	48	sk0	0.74

shows the ID of the analyzed fragment, microorganisms, experimental time of testing, fragment chemical reactivity parameter, statistical correlation coefficient (r) for MIC and softness and electrophilicity fragments, and the atoms (marked in orange) considered in the fragment for series I and II. The basic fragment ID a (g and i) is related with the oxygen atom, fragment ID b (f and h) includes the carbon atom to gets the carbonyl group, fragment ID c includes carbon and nitrogen atoms from pyrrole ring and ipso- and ortho-carbon atoms of the phenyl ring, fragment ID d includes meta and para-carbon atoms of the phenyl ring, and so on. For Aspergillus niger in series I, high correlation values were obtained for s_k⁻ [fragment a = g (oxygen atom, r = 0.90, 48 h) and fragment b = f (carbonyl group, r = 0.93, 48 h)] and s_k⁺ [fragment c (r = 0.98, 72 h) and fragment d (r = 0.95, 48 h)]. As we can observe for Aspergillus niger, the addition of the pyrrole and phenyl fragments to the carbonyl group increases the correlation coefficient for series I (the time of testing more representative for this species was 72 h). For A. fumigatus, linear regressions for s_k⁺ (or s_k⁰) includes the carbonyl group r = 0.83 (or r = 0.82) and the oxygen atom r = 0.81 (or r = 0.80). The more significant time of testing was 48 h.

For series II, C. albicans has the higher correlation values for ω_k⁻; the addition of carbon atom to oxygen atom to obtain the carbonyl group keeps the correlation for ω_k⁻ (see fragments m, r = 0.92 and n, r = 0.92). Fragments that include the nitrogen atom of the pyrrole ring do not increase the correlation value when increasing the number of carbon atoms of the phenyl ring (j, k and l, r = 0.75). The addition of the pyrrole ring, ipso carbon atom, and the meta-C atom from the phenyl ring, improves the correlation (q, r = 0.86). For other species, linear regressions with higher r were found when oxygen was included in ω_k⁰: C. krusei 48 h (r = 0.78), C. tropicalis 24 h (r = 0.78), C. guilliermondii 48 h (r = 0.76), and C. parapsilosis 24 h (r = 0.78).

Additionally, the Parr functions [41,42] were calculated for electrophilic P⁻(r) and nucleophilic P⁺(r) attacks. They had similar tendency than Fukui functions (See Tables S1 and S2).

4.3. MEP and Dipole Moment

Figure 4 shows the molecular electrostatic potential (MEP) for compounds 6, 7a–g and 8a–g. The MEP is a useful descriptor for understanding which sites in the molecules have affinity to a proton (charge controlled hard-hard interactions [43]) and the relative polarity of the molecule [44,45,46,47,48,49,50,51,52]. Regions in red color indicate higher negative charge, higher electron density, and higher affinity to a proton. Regions in blue color indicate more positive charge, a low electron density and a low affinity to a proton. For series I and II, the red region is located near the oxygen atom from carbonyl group, and the blue region is located near the nitrogen atom for both series, and the phenyl group for series I. In general, compounds in series I show a higher dipolar moment than compounds of series II as we can observe in

Table 7. Dipole Moment of indol-4-one; series I compounds 6 and 7a–g and series II compounds 8a–g.

Compound	µ (D)
6	5.98
7a	6.70
7b	7.26
7c	4.86
7d	5.49
7e	7.25
7f	4.73
7g	5.40
8a	5.49
8b	6.69
8c	5.30
8d	4.00
8e	4.47
8f	5.31
8g	4.41

. The dipole moment was calculated for all of the 15 indol-4-ones at the B3LYP/6-311+G (d, p) level of theory. The dipole moment follows the trend: 7b > 7e > 7a > 8b > 6 > 7d = 8a > 7g > 8f > 8c > 7c > 7f > 8e > 8g > 8d. For series I, compound 7b shows the highest value (7.26 D), and, for series II, compound 8b has the highest value (6.69 D). Both compounds present a 2-fluor substitution in the aromatic ring. This can suggest that there is a correlation between the relative polarity of the compounds 6, 7a–g and 8a–g and the kind of interactions that these compounds can have with the active site of the receptor to antifungal activity.

5. Conclusions

Hardness, electronegativity, and electrophilicity of indol-4-ones were the chemical reactivity parameters that had a higher correlation with antifungal activity. Hardness was the index that had higher correlation for series I, and chemical potential, electronegativity, and electrophilicity had higher correlation with antifungal activity for series II.

Fukui function for electrophilic attack had the higher correlation with molecular fragments around both pyrrole and carbonyl groups, suggesting that nature of the reactivity operative between the electrophilic sites of the indol-4-ones and the biologically active site in the studied fungi.

The strongest correlation with biological activity was found with C. albicans, C. glabrata, and A. fumigatus.

The molecular electrostatic potential and the dipole moment calculated for compounds 6, 7a–g and 8a–g suggest that there is a correlation between the relative polarity of the compounds and the kind of interactions that these compounds can have with the active site of the receptor, as has been suggested by González et al.