Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters
Abstract
:1. Introduction
2. Experimental Design and Methods
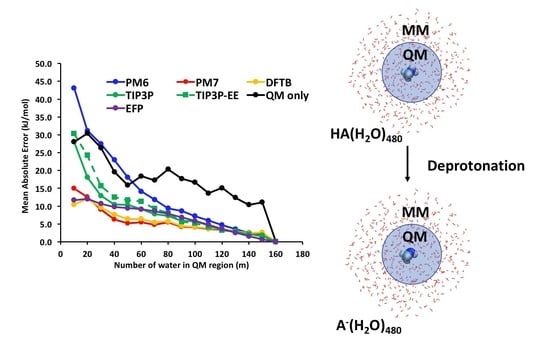
3. Results and Discussion
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lin, H.; Truhlar, D.G. QM/MM: What have we learned, where are we, and where do we go from here? Theor. Chem. Acc. 2006, 117, 185. [Google Scholar] [CrossRef]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Acevedo, O.; Jorgensen, W.L. Advances in Quantum and Molecular Mechanical (QM/MM) simulations for organic and enzymatic reactions. Acc. Chem. Res. 2010, 43, 142–151. [Google Scholar] [CrossRef] [PubMed]
- Van der Kamp, M.W.; Mulholland, A.J. Combined quantum mechanics/molecular mechanics (QM/MM) methods in computational enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar] [CrossRef] [PubMed]
- Brunk, E.; Rothlisberger, U. Mixed Quantum Mechanical/Molecular Mechanical Molecular Dynamics simulations of biological systems in ground and electronically excited states. Chem. Rev. 2015, 115, 6217–6263. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Wang, Y.; Chen, Y.; Field, M.J.; Gao, J. QM/MM through the 1990s: The first twenty years of method development and applications. Isr. J. Chem. 2014, 54, 1250–1263. [Google Scholar] [CrossRef] [PubMed]
- Flaig, D.; Beer, M.; Ochsenfeld, C. Convergence of electronic structure with the size of the QM Region: example of QM/MM NMR shieldings. J. Chem. Theory Comput. 2012, 8, 2260–2271. [Google Scholar] [CrossRef] [PubMed]
- Hartman, J.D.; Neubauer, T.J.; Caulkins, B.G.; Mueller, L.J.; Beran, G.J. Converging nuclear magnetic shielding calculations with respect to basis and system size in protein systems. J. Biomol. NMR 2015, 62, 327–340. [Google Scholar] [CrossRef] [PubMed]
- Nåbo, L.J.; Olsen, J.M.H.; Martínez, T.J.; Kongsted, J. The Quality of the embedding potential is decisive for minimal quantum region size in embedding calculations: The case of the green fluorescent protein. J. Chem. Theory Comput. 2017, 13, 6230–6236. [Google Scholar] [CrossRef] [PubMed]
- Provorse, M.R.; Peev, T.; Xiong, C.; Isborn, C.M. Convergence of excitation energies in mixed quantum and classical solvent: comparison of continuum and point charge models. J. Phys. Chem. B 2016, 120, 12148–12159. [Google Scholar] [CrossRef] [PubMed]
- Milanese, J.M.; Provorse, M.R.; Alameda, E.; Isborn, C.M. Convergence of computed aqueous absorption spectra with explicit quantum mechanical solvent. J. Chem. Theory Comput. 2017, 13, 2159–2171. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.-Z.; Thiel, W. Convergence in the QM-only and QM/MM modeling of enzymatic reactions: A case study for acetylene hydratase. J. Comput. Chem. 2013, 34, 2389–2397. [Google Scholar] [CrossRef] [PubMed]
- Kulik, H.J.; Zhang, J.; Klinman, J.P.; Martínez, T.J. How large should the QM region be in QM/MM calculations? The case of catechol O-methyltransferase. J. Phys. Chem. B 2016, 120, 11381–11394. [Google Scholar] [CrossRef] [PubMed]
- Jindal, G.; Warshel, A. Exploring the dependence of QM/MM calculations of enzyme catalysis on the size of the QM region. J. Phys. Chem. B 2016, 120, 9913–9921. [Google Scholar] [CrossRef] [PubMed]
- Liao, R.-Z.; Thiel, W. Comparison of QM-Only and QM/MM models for the mechanism of tungsten-dependent acetylene hydratase. J. Chem. Theory Comput. 2012, 8, 3793–3803. [Google Scholar] [CrossRef] [PubMed]
- Benediktsson, B.; Bjornsson, R. QM/MM study of the nitrogenase mofe protein resting state: Broken-symmetry states, protonation states, and QM region convergence in the FeMoco active site. Inorg. Chem. 2017, 56, 13417–13429. [Google Scholar] [CrossRef] [PubMed]
- Roßbach, S.; Ochsenfeld, C. Influence of Coupling and embedding schemes on QM size convergence in QM/MM approaches for the example of a proton transfer in DNA. J. Chem. Theory Comput. 2017, 13, 1102–1107. [Google Scholar] [CrossRef] [PubMed]
- Das, S.; Nam, K.; Major, D.T. Rapid convergence of energy and free energy profiles with quantum mechanical size in quantum mechanical-molecular mechanical simulations of proton transfer in DNA. J. Chem. Theory Comput. 2018, 14, 1695–1805. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Söderhjelm, P.; Ryde, U. On the convergence of QM/MM energies. J. Chem. Theory Comput. 2011, 7, 761–777. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods V: Modification of NDDO approximations and application to 70 elements. J. Mol. Model. 2007, 13, 1173–1213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stewart, J.J.P. Optimization of parameters for semiempirical methods VI: More modifications to the NDDO approximations and re-optimization of parameters. J. Mol. Model. 2013, 19, 1–32. [Google Scholar] [CrossRef] [PubMed]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, M.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density-functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260. [Google Scholar] [CrossRef]
- Pruitt, S.R.; Bertoni, C.; Brorsen, K.R.; Gordon, M.S. Efficient and Accurate fragmentation methods. Acc. Chem. Res. 2014, 47, 2786–2794. [Google Scholar] [CrossRef] [PubMed]
- Gordon, M.S.; Fedorov, D.G.; Pruitt, S.R.; Slipchenko, L.V. Fragmentation methods: A route to accurate calculations on large systems. Chem. Rev. 2012, 112, 632–672. [Google Scholar] [CrossRef] [PubMed]
- Gordon, M.S.; Mullin, J.M.; Pruitt, S.R.; Roskop, L.B.; Slipchenko, L.V.; Boatz, J.A. Accurate methods for large molecular systems. J. Phys. Chem. B 2009, 113, 9646–9663. [Google Scholar] [CrossRef] [PubMed]
- Zheng, G.; Witek, H.A.; Bobadova-Parvanova, P.; Irle, S.; Musaev, D.G.; Prabhakar, R.; Morokuma, K.; Lundberg, M.; Elstner, M.; Köhler, C.; Frauenheim, T. Parameter calibration of transition-metal elements for the spin-polarized self-consistent-charge density-functional tight-binding (DFTB) method: Sc, Ti, Fe, Co, and Ni. J. Chem. Theory Comput. 2007, 3, 1349–1367. [Google Scholar] [CrossRef] [PubMed]
- Chung, L.W.; Sameera, W.M.C.; Ramozzi, R.; Page, A.J.; Hatanaka, M.; Petrova, G.P.; Harris, T.V.; Li, X.; Ke, Z.; Liu, F.; et al. The ONIOM method and Its applications. Chem. Rev. 2015, 115, 5678–5796. [Google Scholar] [CrossRef] [PubMed]
- Chung, L.W.; Hirao, H.; Li, X.; Morokuma, K. The ONIOM method: Its foundation and applications to metalloenzymes and photobiology. WIRES Comput. Mol. Sci. 2011, 2, 327–350. [Google Scholar] [CrossRef]
- Vreven, T.; Morokuma, K. Hybrid methods: ONIOM(QM:MM) and QM/MM. Annu. Rep. Comput. Chem. 2006, 2, 35–51. [Google Scholar]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general AMBER force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Kollman, P.A. Application of RESP charges to calculate conformational energies, hydrogen bond energies, and free energies of solvation. JACS 1993, 115, 9620–9631. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Gordon, M.S.; Schmidt, M.W. Advances in electronic structure theory: GAMESS a decade later. In Theory and Applications of Computational Chemistry: The First Forty Years; Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Ghosh, D.; Kosenkov, D.; Vanovschi, V.; Flick, J.; Kaliman, I.; Shao, Y.; Gilbert, A.T.B.; Krylov, A.I.; Slipchenko, L.V. Effective fragment potential method in Q-CHEM: A guide for users and developers. J. Comput. Chem. 2013, 34, 1060–1070. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; Gan, Z.; Epifanovsky, E.; Gilbert, A.T.B.; Wormit, M.; Kussmann, J.; Lange, A.W.; Behn, A.; Deng, J.; Feng, X.; et al. Advances in molecular quantum chemistry contained in the Q-Chem 4 program package. Mol. Phys. 2015, 113, 184–215. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mackerell, A.D.J.; Bashford, D.; Bellott, M.; Dunbrack, R.L.J.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Cao, L.; Ryde, U. On the difference between additive and subtractive QM/MM calculations. Front. Chem. 2018, 6, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Tissandier, M.D.; Cowen, K.A.; Feng, W.Y.; Gundlach, E.; Cohen, M.H.; Earhart, A.D.; Coe, J.V.; Tuttle, T.R., Jr. The proton’s absolute aqueous enthalpy and gibbs free energy of solvation from cluster-ion solvation data. J. Phys. Chem. A 1998, 102, 7787–7794. [Google Scholar] [CrossRef]
- Karelina, M.; Kulik, H.J. Systematic quantum mechanical region determination in QM/MM simulation. J. Chem. Theory Comput. 2017, 13, 563–576. [Google Scholar] [CrossRef] [PubMed]





| Theory | CH3NH3+ | Phenol | ||
|---|---|---|---|---|
| Frame 0 | Frame 10 | Frame 0 | Frame 10 | |
| ωB97X-D/6-31G(d) | 296.0 (0.0) | 206.7 (0.0) | −31.2 (0.0) | −46.9 (0.0) |
| AMBER/TIP3P | 258.2 (−37.9) | 173.3 (−33.4) | −5.1 (26.2) | −1.3 (45.7) |
| PM7 | 240.9 (−55.2) | 172.9 (−33.7) | −18.1 (13.2) | −24.8 (22.1) |
| DFTB | 226.5 (−69.5) | 156.5 (−50.1) | −18.9 (12.4) | −32.6 (14.3) |
| HF/6-31G(d) | 296.9 (0.9) | 204.8 (−1.9) | −28.7 (2.5) | −51.4 (-4.4) |
| Method | HCOOH | C6H5OH | CH3NH3+ | H-Imidazole+ |
|---|---|---|---|---|
| QM-only | >150 (28.0) | 150 (35.0) | 150 (204.9) | 150 (168.8) |
| TIP3P | 60 (28.0) | 50 (32.9) | 60 (32.5) | 50 (14.6) |
| TIP3P-EE | 70 (30.3) | 70 (32.5) | 30 (21.0) | 30 (11.0) |
| EFP | 40 (11.7) | 10 (8.9) | 10 (5.1) | 10 (7.5) |
| PM6 | 80 (43.1) | 100 (39.1) | 110 (79.9) | 110 (71.0) |
| PM7 | 30 (14.9) | 40 (17.0) | 70 (36.1) | 60 (22.3) |
| DFTB | 30 (10.4) | 40 (11.4) | 70 (45.2) | 70 (35.0) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ho, J.; Shao, Y.; Kato, J. Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters. Molecules 2018, 23, 2466. https://doi.org/10.3390/molecules23102466
Ho J, Shao Y, Kato J. Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters. Molecules. 2018; 23(10):2466. https://doi.org/10.3390/molecules23102466
Chicago/Turabian StyleHo, Junming, Yihan Shao, and Jin Kato. 2018. "Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters" Molecules 23, no. 10: 2466. https://doi.org/10.3390/molecules23102466
APA StyleHo, J., Shao, Y., & Kato, J. (2018). Do Better Quality Embedding Potentials Accelerate the Convergence of QM/MM Models? The Case of Solvated Acid Clusters. Molecules, 23(10), 2466. https://doi.org/10.3390/molecules23102466