An Ab Initio QM/MM Study of the Electrostatic Contribution to Catalysis in the Active Site of Ketosteroid Isomerase
Abstract
:1. Introduction
2. Computational Approaches
2.1. QM/MM MD Simulations of the Wild-Type and Mutants of KSI
2.2. Calculations of the Electric Field with the Amber ff99SB Force Field
2.3. Calculations of the Electric Field with the EE-GMFCC Method
2.4. Classical MD Simulation and Calculation of the Electric Fields
3. Results and Discussion
3.1. The QM Effect is Important for Description of the Electrostatics in H-Bonding Environment
3.2. Calculation of Electric Fields
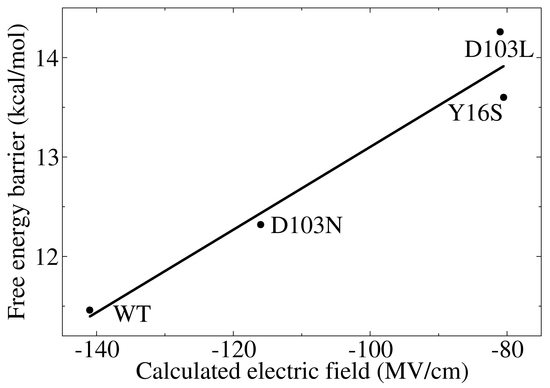
3.3. Electrostatic Contribution to Catalysis in KSI
3.4. Decomposition of the Electric Field
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hilvert, D. Critical analysis of antibody catalysis. Annu. Rev. Biochem. 2000, 69, 751–793. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Sharma, P.K.; Kato, M.; Xiang, Y.; Liu, H.; Olsson, M.H. Electrostatic basis for enzyme catalysis. Chem. Rev. 2006, 106, 3210–3235. [Google Scholar] [CrossRef] [PubMed]
- Aragonès, A.C.; Haworth, N.L.; Darwish, N.; Ciampi, S.; Bloomfield, N.J.; Wallace, G.G.; Diez-Perez, I.; Coote, M.L. Electrostatic catalysis of a Diels–Alder reaction. Nature 2016, 531, 88–91. [Google Scholar] [CrossRef] [PubMed]
- Fried, S.D.; Boxer, S.G. Measuring Electric Fields and Noncovalent Interactions Using the Vibrational Stark Effect. Acc. Chem. Res. 2015, 48, 998–1006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fried, S.D.; Bagchi, S.; Boxer, S.G. Extreme electric fields power catalysis in the active site of ketosteroid isomerase. Science 2014, 346, 1510–1514. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.F.; Boxer, S.G. A Critical Test of the Electrostatic Contribution to Catalysis with Noncanonical Amino Acids in Ketosteroid Isomerase. J. Am. Chem. Soc. 2016, 138, 11890–11895. [Google Scholar] [CrossRef] [PubMed]
- Schneider, S.H.; Boxer, S.G. Vibrational Stark Effects of Carbonyl Probes Applied to Reinterpret IR and Raman Data for Enzyme Inhibitors in Terms of Electric Fields at the Active Site. J. Phys. Chem. B 2016, 120, 9672–9684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.W.; Zhang, J.Z.H.; He, X. Ab initio Quantum Mechanics/Molecular Mechanics Molecular Dynamics Simulation of CO in the Heme Distal Pocket of Myoglobin. Chin. J. Chem. Phys. 2017, 30, 705–716. [Google Scholar] [CrossRef]
- Park, E.S.; Andrews, S.S.; Hu, R.B.; Boxer, S.G. Vibrational stark spectroscopy in proteins: A probe and calibration for electrostatic fields. J. Phys. Chem. B 1999, 103, 9813–9817. [Google Scholar] [CrossRef]
- Nienhaus, K.; Olson, J.S.; Franzen, S.; Nienhaus, G.U. The origin of stark splitting in the initial photoproduct state of MbCO. J. Am. Chem. Soc. 2005, 127, 40–41. [Google Scholar] [CrossRef] [PubMed]
- Plattner, N.; Meuwly, M. The role of higher CO-multipole moments in understanding the dynamics of photodissociated carbonmonoxide in myoglobin. Biophys. J. 2008, 94, 2505–2515. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.W.; He, X.; Zhang, J.Z.H. Predicting Mutation-Induced Stark Shifts in the Active Site of a Protein with a Polarized Force Field. J. Phys. Chem. A 2013, 117, 6015–6023. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Cohen, A.E.; Boxer, S.G. Electrostatic Fields near the Active Site of Human Aldose Reductase: 2. New Inhibitors and Complications Caused by Hydrogen Bonds. Biochemistry 2011, 50, 8311–8322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kraft, M.L.; Weber, P.K.; Longo, M.L.; Hutcheon, I.D.; Boxer, S.G. Phase separation of lipid membranes analyzed with high-resolution secondary ion mass spectrometry. Science 2006, 313, 1948–1951. [Google Scholar] [CrossRef] [PubMed]
- Webb, L.J.; Boxer, S.G. Electrostatic fields near the active site of human aldose reductase: 1. New inhibitors and vibrational stark effect measurements. Biochemistry 2008, 47, 1588–1598. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.W.; Zhang, J.Z.H.; He, X. Quantum mechanical calculation of electric fields and vibrational Stark shifts at active site of human aldose reductase. J. Chem. Phys. 2015, 143, 184111. [Google Scholar] [CrossRef] [PubMed]
- Andrews, S.S.; Boxer, S.G. Vibrational stark effects of nitriles I. Methods and experimental results. J. Phys. Chem. A 2000, 104, 11853–11863. [Google Scholar] [CrossRef]
- Choi, J.-H.; Oh, K.-I.; Lee, H.; Lee, C.; Cho, M. Nitrile and thiocyanate IR probes: Quantum chemistry calculation studies and multivariate least-square fitting analysis. J. Chem. Phys. 2008, 128, 134506. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.-H.; Cho, M. Vibrational solvatochromism and electrochromism of infrared probe molecules containing C≡O, C≡N, C=O, or C−F vibrational chromophore. J. Chem. Phys. 2011, 134, 154513. [Google Scholar] [CrossRef] [PubMed]
- Fried, S.D.; Bagchi, S.; Boxer, S.G. Measuring Electrostatic Fields in Both Hydrogen-Bonding and Non-Hydrogen-Bonding Environments Using Carbonyl Vibrational Probes. J. Am. Chem. Soc. 2013, 135, 11181–11192. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radzicka, A.; Wolfenden, R. A proficient enzyme. Science 1995, 267, 90–93. [Google Scholar] [CrossRef] [PubMed]
- Pollack, R.M. Enzymatic mechanisms for catalysis of enolization: Ketosteroid isomerase. Bioorg. Chem. 2004, 32, 341–353. [Google Scholar] [CrossRef] [PubMed]
- Ji, C.; Mei, Y.; Zhang, J.Z. Developing polarized protein-specific charges for protein dynamics: MD free energy calculation of pK a shifts for Asp 26/Asp 20 in Thioredoxin. Biophys. J. 2008, 95, 1080–1088. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.L.; Mei, Y.; Zhang, D.; Zhang, Q.G.; Zhang, J.Z. Folding of a helix at room temperature is critically aided by electrostatic polarization of intraprotein hydrogen bonds. J. Am. Chem. Soc. 2010, 132, 11159–11164. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Cieplak, P.; Li, J.; Wang, J.; Cai, Q.; Hsieh, M.; Lei, H.; Luo, R.; Duan, Y. Development of polarizable models for molecular mechanical calculations II: Induced dipole models significantly improve accuracy of intermolecular interaction energies. J. Phys. Chem. B 2011, 115, 3100–3111. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.L.; Gao, Y.; Mei, Y.; Zhang, Q.G.; Tang, B.; Zhang, J.Z. Folding of a helix is critically stabilized by polarization of backbone hydrogen bonds: Study in explicit water. J. Phys. Chem. B 2012, 116, 3430–3435. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.L.; Zhu, T.; Zhang, Q.G.; Tang, B.; Zhang, J.Z. Electronic polarization stabilizes tertiary structure prediction of HP-36. J. Mol. Model. 2014, 20, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Ji, C.; Mei, Y. Some practical approaches to treating electrostatic polarization of proteins. Acc. Chem. Res. 2014, 47, 2795–2803. [Google Scholar] [CrossRef] [PubMed]
- DeLano, W.L. The PyMOL Molcular Graphics System, version 1.5.0.1; DeLano Scientific: San Carlos, CA, USA, 2012. [Google Scholar]
- Case, D.A.; Cheatham, T.E.; Darden, T.; Gohlke, H.; Luo, R.; Merz, K.M.; Onufriev, A.; Simmerling, C.; Wang, B.; Woods, R.J. The Amber biomolecular simulation programs. J. Comput. Chem. 2005, 26, 1668–1688. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, J.M.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.M.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bayly, C.I.; Cieplak, P.; Cornell, W.D.; Kollman, P.A. A Well-behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Ryckaert, J.-P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Pastor, R.W.; Brooks, B.R.; Szabo, A. An analysis of the accuracy of Langevin and molecular dynamics algorithms. Mol. Phys. 1988, 65, 1409–1419. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Walker, M.; Harvey, A.J.A.; Sen, A.; Dessent, C.E.H. Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions. J. Phys. Chem. A 2013, 117, 12590–12600. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Pitonak, M.; Cerny, J.; Hobza, P. On the Structure and Geometry of Biomolecular Binding Motifs (Hydrogen-Bonding, Stacking, X−H···π): WFT and DFT Calculations. J. Chem. Theory Comput. 2010, 6, 66–80. [Google Scholar] [CrossRef] [PubMed]
- Field, M.J.; Bash, P.A.; Karplus, M. A Combined Quantum Mechanical and Molecular Mechanical Potential for Molecular Dynamics Simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Latouche, C.; Akdas-Kilig, H.; Malval, J.P.; Fillaut, J.L.; Boucekkine, A.; Barone, V. Theoretical evidence of metal-induced structural distortions in a series of bipyrimidine-based ligands. Dalton Trans. 2015, 44, 506–510. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Schutz, C.N.; Warshel, A. What are the dielectric “constants” of proteins and how to validate electrostatic models? Proteins Struct. Funct. Bioinform. 2001, 44, 400–417. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhang, J.Z.H. A new method for direct calculation of total energy of protein. J. Chem. Phys. 2005, 122, 031103. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhang, J.Z.H. The generalized molecular fractionation with conjugate caps/molecular mechanics method for direct calculation of protein energy. J. Chem. Phys. 2006, 124, 184703. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Liu, J.; Zhang, J.Z.; He, X. Electrostatically embedded generalized molecular fractionation with conjugate caps method for full quantum mechanical calculation of protein energy. J. Phys. Chem. A 2013, 117, 7149–7161. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.Y.; Wang, X.W.; Liu, J.F.; Zhang, J.Z.H.; Mei, Y.; He, X. An improved fragment-based quantum mechanical method for calculation of electrostatic solvation energy of proteins. J. Chem. Phys. 2013, 139, 214104. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Zhu, T.; Wang, X.; Liu, J.; Zhang, J.Z. Fragment quantum mechanical calculation of proteins and its applications. Acc. Chem. Res. 2014, 47, 2748–2757. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.A.; Bettens, R.P. Energy-based molecular fragmentation methods. Chem. Rev. 2015, 115, 5607–5642. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.F.; Wang, X.W.; Zhang, J.Z.H.; He, X. Calculation of protein-ligand binding affinities based on a fragment quantum mechanical method. RSC Adv. 2015, 5, 107020–107030. [Google Scholar] [CrossRef]
- Liu, J.F.; Zhu, T.; Wang, X.W.; He, X.; Zhang, J.Z.H. Quantum Fragment Based ab Initio Molecular Dynamics for Proteins. J. Chem. Theory Comput. 2015, 11, 5897–5905. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.F.; Zhang, J.Z.H.; He, X. Fragment quantum chemical approach to geometry optimization and vibrational spectrum calculation of proteins. Phys. Chem. Chem. Phys. 2016, 18, 1864–1875. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.S.; Zhang, J.Z.H.; He, X. Full QM Calculation of RNA Energy Using Electrostatically Embedded Generalized Molecular Fractionation with Conjugate Caps Method. J. Phys. Chem. A 2017, 121, 2503–2514. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.Q.; Liu, J.F.; Li, J.J.; He, X. Fragment-based quantum mechanical calculation of protein-protein binding affinities. J. Comput. Chem. 2018, 39, 1617–1628. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.W.; Li, Y.; Gao, Y.; Yang, Z.J.; Lu, C.H.; Zhu, T. A quantum mechanical computational method for modeling electrostatic and solvation effects of protein. Sci. Rep. 2018, 8, 5475. [Google Scholar] [CrossRef] [PubMed]
- Cornell, W.D.; Cieplak, P.; Bayly, C.I.; Kollman, P.A. Application of RESP Charges to Calculate Conformational Energies, Hydrogen Bond Energies, and Free Energies of Solvation. J. Am. Chem. Soc. 1993, 115, 9620–9631. [Google Scholar] [CrossRef]
- Sandberg, D.J.; Rudnitskaya, A.N.; Gascon, J.A. QM/MM Prediction of the Stark Shift in the Active Site of a Protein. J. Chem. Theory Comput. 2012, 8, 2817–2823. [Google Scholar] [CrossRef] [PubMed]
- Duan, L.L.; Feng, G.Q.; Zhang, Q.G. Large-scale molecular dynamics simulation: Effect of polarization on thrombin-ligand binding energy. Sci. Rep. 2016, 6, 31488. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Suydam, I.T.; Snow, C.D.; Pande, V.S.; Boxer, S.G. Electric fields at the active site of an enzyme: Direct comparison of experiment with theory. Science 2006, 313, 200–204. [Google Scholar] [CrossRef] [PubMed]
- Fuxreiter, M.; Warshel, A. Origin of the catalytic power of acetylcholinesterase: Computer simulation studies. J. Am. Chem. Soc. 1998, 120, 183–194. [Google Scholar] [CrossRef]
- Quinn, D.M. Acetylcholinesterase: Enzyme structure, reaction dynamics, and virtual transition states. Chem. Rev. 1987, 87, 955–979. [Google Scholar] [CrossRef]






| Model | Exp. [5] | MM | QM/MM + FF | QM/MM + QM |
|---|---|---|---|---|
| WT | −144 | −100 | −124 | −141 |
| D103N | −134 | −66 | −93 | −116 |
| WT | D103N | Y16S | D103L | |
|---|---|---|---|---|
| RES 16 | −47 | −46 | −2 | −45 |
| RES 103 | −52 | −36 | −51 | −4 |
| RES 40 | −26 | −29 | −22 | −23 |
| Sum of 3RS | −125 | −111 | −75 | −72 |
| Sum of ARS | −124 | −93 | −74 | −66 |
| Solvent | 7 | 10 | 8 | 9 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; He, X. An Ab Initio QM/MM Study of the Electrostatic Contribution to Catalysis in the Active Site of Ketosteroid Isomerase. Molecules 2018, 23, 2410. https://doi.org/10.3390/molecules23102410
Wang X, He X. An Ab Initio QM/MM Study of the Electrostatic Contribution to Catalysis in the Active Site of Ketosteroid Isomerase. Molecules. 2018; 23(10):2410. https://doi.org/10.3390/molecules23102410
Chicago/Turabian StyleWang, Xianwei, and Xiao He. 2018. "An Ab Initio QM/MM Study of the Electrostatic Contribution to Catalysis in the Active Site of Ketosteroid Isomerase" Molecules 23, no. 10: 2410. https://doi.org/10.3390/molecules23102410
APA StyleWang, X., & He, X. (2018). An Ab Initio QM/MM Study of the Electrostatic Contribution to Catalysis in the Active Site of Ketosteroid Isomerase. Molecules, 23(10), 2410. https://doi.org/10.3390/molecules23102410