Exploring Peptide–Solvent Interactions: A Computational Study
Abstract
:1. Introduction
2. Methods
2.1. Preparation of XAO and 9-Mer Polypeptides
2.2. MD Simulations
2.3. QM/MM Energy Function
2.4. Calculating Theoretical Scattering Profiles and Effective R Values
3. Results and Discussion
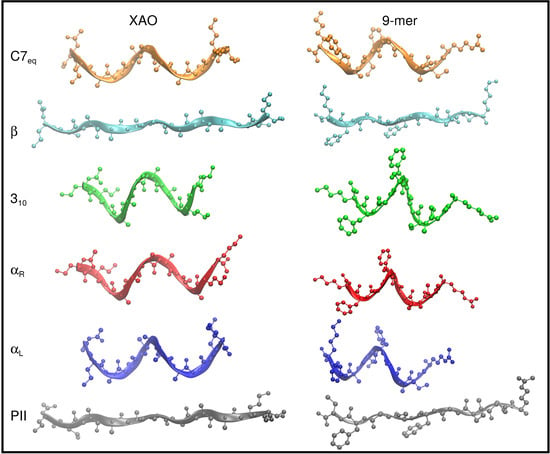
3.1. Dihedral Angle Distribution
3.2. End-to-End Distance, R
4. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| QM/MM | quantum mechanics/molecular mechanics |
| MD | molecular dynamics |
| XAO | XAO, X = diaminobutyric acid, A = alanine, and O = ornithine |
References
- Creighton, T.E. Proteins: Structure and Molecular Properties, 2nd ed.; W. H. Freeman and Company: New York, NY, USA, 1993. [Google Scholar]
- Makowska, J.; Rodziewicz-Motowidło, S.; Bagińska, K.; Makowski, M.; Vila, J.A.; Liwo, A.; Chmurzyński, L.; Scheraga, H.A. Further evidence for the absence of polyproline II stretch in the XAO peptide. Biophys. J. 2007, 92, 2904–2917. [Google Scholar] [CrossRef] [PubMed]
- Kelly, M.A.; Chellgren, B.W.; Rucker, A.L.; Troutman, J.M.; Fried, M.G.; Miller, A.-F.; Creamer, T.P. Host-guest study of left-handed polyproline II helix formation. Biochemistry 2001, 40, 14376–14383. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Olson, C.A.; Rose, G.D.; Baldwin, R.L.; Kallenbach, N.R. Polyproline II structure in a sequence of seven alanine residues. Proc. Natl. Acad. Sci. USA 2002, 99, 9190–9195. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kentsis, A.; Mezei, M.; Gindin, T.; Osman, R. Unfolded state of polyalanine is a segmented polyprolin e II helix. Proteins Struct. Funct. Bioinfor. 2004, 55, 493–501. [Google Scholar] [CrossRef] [PubMed]
- Makowska, J.; Rodziewicz-Motowidło, S.; Bagińska, K.; Vila, J.A.; Liwo, A.; Chmurzyński, L.; Scheraga, H.A. Polyproline II conformation is one of many local conformational states and is not an over all conformation of unfolded peptides and proteins. Proc. Natl. Acad. Sci. USA 2006, 103, 1744–1749. [Google Scholar] [CrossRef] [PubMed]
- Zagrovic, B.; Lipfert, J.; Sorin, E.J.; Millett, I.S.; van Gunsteren, W.F.; Doniach, S.; Pande, V.S. Unusual compactness of a polyproline type II structure. Proc. Natl. Acad. Sci. USA 2005, 102, 11698–11703. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mikhonin, A.V.; Bykov, S.V.; Myshakina, N.S.; Asher, S.A. Peptide secondary structure folding reaction coordinate: Correlation between UV Raman amide III frequ ency, Ψ Ramachandran angle, and hydrogen bonding. J. Phys. Chem. B 2006, 110, 1928–1943. [Google Scholar] [CrossRef] [PubMed]
- Jha, A.K.; Colubri, A.; Freed, K.F.; Sosnick, T.R. Statistical coil model of the unfolded state: Resolving the reconciliation problem. Proc. Natl. Acad. Sci. USA 2005, 102, 13099–13104. [Google Scholar] [CrossRef] [PubMed]
- Schweitzer-Stenner, R.; Measey, T.J. The alanine-rich XAO peptide adopts a heterogeneous population, including turn-like and polyproline II conformations. Proc. Natl. Acad. Sci. USA 2007, 104, 6649–6654. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Prabhu, N.; Sharp, K. Protein-solvent interactions. Chem. Rev. 2006, 106, 1616–1623. [Google Scholar] [CrossRef] [PubMed]
- Mantz, Y.A.; Gerard, H.; Iftimie, R.; Martyna, G.J. Ab initio and empirical model MD simulation studies of solvent effects on the properties of N-methylacetamide along a cis-trans isomerization pathway. J. Phys. Chem. B 2006, 110, 13523–13538. [Google Scholar] [CrossRef] [PubMed]
- Blanco, S.; López, J.C.; Lesarri, A.; Alonso, J.L. Microsolvation of formamide: A rotational study. J. Am. Chem. Soc. 2006, 128, 12111–12121. [Google Scholar] [CrossRef] [PubMed]
- Ishida, H. Essential function of the N-termini tails of the proteasome for the gating mechanism revealed by molecular dynamics simulations. Proteins 2014, 82, 1985–1999. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, A.D., Jr. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone ϕ, ψ and side-chain χ1 and χ2 dihedral angles. J. Chem. Theory Comp. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Feig, M.; Brooks, C.L., III. Improved treatment of the protein backbone in empirical force fields. J. Am. Chem. Soc. 2004, 126, 698–699. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Mittal, J.; Feig, M.; MacKerell, A.D., Jr. Inclusion of many-body effects in the additive CHARMM protein CMAP potential results in enhanced cooperativity of α-helix and β-hairpin formation. Biophys. J. 2012, 103, 1045–1051. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmuller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Meth. 2017, 14, 71–73. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.; Chandrasekhar, J.; Madura, J.; Impey, R.; Klein, M. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comp. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J.C. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Pastor, R.W.; Brooks, B.R.; Szabo, A. An analysis of the accuracy of Langevin and molecular dynamics algorithms. Mol. Phys. 1988, 65, 1409–1419. [Google Scholar] [CrossRef]
- Ramachandran, G.N.; Sasiskharan, V. Conformation of polypeptides and proteins. Adv. Protein Chem. 1968, 23, 283–437. [Google Scholar] [PubMed]
- Field, M.J.; Bash, P.A.; Karplus, M. A combined quantum mechanical and molecular mechanical potential for molecular dynamics simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Singh, U.C.; Kollman, P.A. A combined ab initio quantum mechanical and molecular mechanical method for carrying out simulations on complex molecular systems: Applications to the CH3Cl + Cl exchange reaction and gas phase protonation of polyethers. J. Comput. Chem. 1986, 7, 718–730. [Google Scholar] [CrossRef]
- Warshel, A. A Computer Modeling of Chemical Reactions in Enzymes and Solutions; John Wiley & Sons: New York, NY, USA, 1991. [Google Scholar]
- Elstner, M.; Porezag, D.; Jungnickel, G.; Elsner, J.; Haugk, M.; Frauenheim, T.; Suhai, S.; Seifert, G. Self-consistent-charge density functional tight-binding method for simulations of complex materials properties. Phys. Rev. B 1998, 58, 7260–7268. [Google Scholar] [CrossRef]
- Cui, Q.; Elstner, M.; Kaxiras, E.; Frauenheim, T.; Karplus, M. A QM/MM implementa tion of the self-consistent charge density functional tight binding (SCC-DFTB) method. J. Phys. Chem. B 2011, 105, 569–585. [Google Scholar] [CrossRef]
- Pu, J.; Gao, J.; Truhlar, D.G. Combining self-consistent-charge density-functional tight-binding (SCC-DFTB) with molecular mechanics by the generalized hybrid orbital (GHO) method. J. Phys. Chem. A 2004, 108, 5454–5463. [Google Scholar] [CrossRef]
- Elstner, M.; Frauenheim, T.; Kaxiras, E.; Seifert, G.; Suhai, S. A self-consistent-charge density functional based tight-binding scheme for large biomolecules. Phys. Stat. Sol. B 2000, 217, 357–376. [Google Scholar] [CrossRef]
- Han, W.-G.; Elstner, M.; Jalkanen, K.J.; Frauenheim, T.; Suhai, S. Hybrid SCC-DFTB/molecular mechanical studies of H-bonded systems and of N-acetyl-(L-Ala)n N’-methylamide helices in water solution. Int. J. Quant. Chem. 2000, 78, 459–479. [Google Scholar] [CrossRef]
- Svergun, D.I.; Barberato, C.; Koch, M.H.J. CRYSOL—A Program to Evaluate X-ray Solution Scattering of Biological Macromolecules from Atomic Coordinates. J. Appl. Cryst. 1995, 28, 768–773. [Google Scholar] [CrossRef]
- Mansiaux, Y.; Joseph, A.P.; Gelly, J.-C.; de Brevern, A.G. Assignment of polyproline II conformation and analysis of sequence-structure relationship. PLoS ONE 2011, 6, e18401. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern of recognition of hydrogen-bonden and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Lipfert, J.; LMU München. Personal communication, 2014.






| Geometry | Relative Population (In Vacuo) | Free Energy Difference [kcal/mol] | Average QM/MM Energy [kcal/mol] | ||
|---|---|---|---|---|---|
| ine | |||||
| P | −180 < < 0 | 135 ≤ ≤ 180 | 0.534 | 0.00 | −111,479 |
| (0.420) | |||||
| ine | |||||
| −180 < < 0 | 50 ≤ < 135 | 0.202 | 0.58 | −111,479 | |
| (0.147) | |||||
| ine | |||||
| −180 < < 0 | −180 ≤ < −25 | 0.126 | 0.86 | −111,475 | |
| (0.150) | |||||
| ine | |||||
| 3 | −180 < < 0 | −25 ≤ < 0 | 0.062 | 1.28 | −111,475 |
| (0.035) | |||||
| ine | |||||
| 0≤ < −180 | −180 ≤≤ 180 | 0.041 | 1.53 | −111,478 | |
| (0.220) | |||||
| ine | |||||
| C7 | −180 < < 0 | 0 ≤ < 50 | 0.035 | 1.62 | −111,478 |
| (0.027) |
| Geometry | Relative Population | Free Energy Difference [kcal/mol] | Average QM/MM Energy [kcal/mol] | ||
|---|---|---|---|---|---|
| ine | |||||
| P | −180 < < 0 | 135 ≤ ≤ 180 | 0.440 | 0 | −111,092 |
| ine | |||||
| 3 | −180 < < 0 | −25 ≤ < 0 | 0.167 | 0.58 | −111,101 |
| ine | |||||
| −180 < < 0 | 50 ≤ < 135 | 0.147 | 0.65 | −111,092 | |
| ine | |||||
| −180 < < 0 | −180 ≤ < −25 | 0.105 | 0.86 | −111,084 | |
| ine | |||||
| C7 | −180 < < 0 | 0 ≤ < 50 | 0.099 | 0.89 | −111,096 |
| ine | |||||
| 0≤ < −180 | −180 ≤≤ 180 | 0.042 | 1.41 | −111,078 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elghobashi-Meinhardt, N. Exploring Peptide–Solvent Interactions: A Computational Study. Molecules 2018, 23, 2355. https://doi.org/10.3390/molecules23092355
Elghobashi-Meinhardt N. Exploring Peptide–Solvent Interactions: A Computational Study. Molecules. 2018; 23(9):2355. https://doi.org/10.3390/molecules23092355
Chicago/Turabian StyleElghobashi-Meinhardt, Nadia. 2018. "Exploring Peptide–Solvent Interactions: A Computational Study" Molecules 23, no. 9: 2355. https://doi.org/10.3390/molecules23092355
APA StyleElghobashi-Meinhardt, N. (2018). Exploring Peptide–Solvent Interactions: A Computational Study. Molecules, 23(9), 2355. https://doi.org/10.3390/molecules23092355