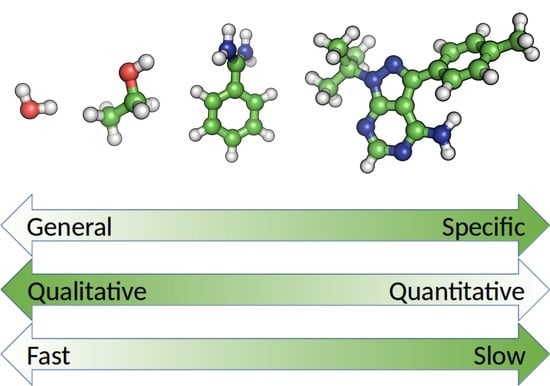
Solvents to Fragments to Drugs: MD Applications in Drug Design
Abstract
:1. Introduction
2. Solvent Structure as a Predictor of Protein-Ligand Interaction Sites
3. Mixed Solvents Simulations in Drug Design
4. Small Ligands and Fragment Screening
5. Molecular Dynamics Simulations of Drugs or Drug-Like Compounds
6. Conclusions and Perspectives
Author Contributions
Funding
Conflicts of Interest
References
- Jorgensen, W.L. The many roles of computation in drug discovery. Science 2004, 303, 1813–1818. [Google Scholar] [CrossRef] [PubMed]
- Sliwoski, G.; Kothiwale, S.; Meiler, J.; Lowe, E.W., Jr. Computational methods in drug discovery. Pharmacol. Rev. 2014, 66, 334–395. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.G.; Boström, J. Where Do Recent Small Molecule Clinical Development Candidates Come From? J. Med. Chem. 2018, 61, 9442–9468. [Google Scholar] [CrossRef] [PubMed]
- Bottaro, S.; Lindorff-Larsen, K. Biophysical experiments and biomolecular simulations: A perfect match? Science 2018, 361, 355–360. [Google Scholar] [CrossRef] [PubMed]
- Lazaridis, T. Inhomogeneous Fluid Approach to Solvation Thermodynamics. 1. Theory. J. Phys. Chem. B 1998, 102, 3531–3541. [Google Scholar] [CrossRef] [Green Version]
- Pan, A.C.; Xu, H.; Palpant, T.; Shaw, D.E. Quantitative Characterization of the Binding and Unbinding of Millimolar Drug Fragments with Molecular Dynamics Simulations. J. Chem. Theory Comput. 2017, 13, 3372–3377. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.H.; Hsin, J.; Sotomayor, M.; Comellas, G.; Schulten, K. Discovery through the computational microscope. Structure 2009, 17, 1295–1306. [Google Scholar] [CrossRef] [PubMed]
- Goodford, P.J. A computational procedure for determining energetically favorable binding sites on biologically important macromolecules. J. Med. Chem. 1985, 28, 849–857. [Google Scholar] [CrossRef]
- Miranker, A.; Karplus, M. Functionality maps of binding sites: A multiple copy simultaneous search method. Proteins 1991, 11, 29–34. [Google Scholar] [CrossRef]
- Brenke, R.; Kozakov, D.; Chuang, G.-Y.; Beglov, D.; Hall, D.; Landon, M.R.; Mattos, C.; Vajda, S. Fragment-based identification of druggable “hot spots” of proteins using Fourier domain correlation techniques. Bioinformatics 2009, 25, 621–627. [Google Scholar] [CrossRef]
- Baum, B.; Muley, L.; Smolinski, M.; Heine, A.; Hangauer, D.; Klebe, G. Non-additivity of functional group contributions in protein-ligand binding: A comprehensive study by crystallography and isothermal titration calorimetry. J. Mol. Biol. 2010, 397, 1042–1054. [Google Scholar] [CrossRef] [PubMed]
- Biela, A.; Betz, M.; Heine, A.; Klebe, G. Water Makes the Difference: Rearrangement of Water Solvation Layer Triggers Non-additivity of Functional Group Contributions in Protein--Ligand Binding. ChemMedChem. 2012, 7, 1423–1434. [Google Scholar] [CrossRef] [PubMed]
- Eastman, P.; Swails, J.; Chodera, J.D.; McGibbon, R.T.; Zhao, Y.; Beauchamp, K.A.; Wang, L.-P.; Simmonett, A.C.; Harrigan, M.P.; Stern, C.D.; et al. OpenMM 7: Rapid development of high performance algorithms for molecular dynamics. PLoS Comput. Biol. 2017, 13, e1005659. [Google Scholar] [CrossRef] [PubMed]
- Kutzner, C.; Páll, S.; Fechner, M.; Esztermann, A.; de Groot, B.L.; Grubmüller, H. Best bang for your buck: GPU nodes for GROMACS biomolecular simulations. J. Comput. Chem. 2015, 36, 1990–2008. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, T.-S.; Cerutti, D.S.; Mermelstein, D.; Lin, C.; LeGrand, S.; Giese, T.J.; Roitberg, A.; Case, D.A.; Walker, R.C.; York, D.M. GPU-Accelerated Molecular Dynamics and Free Energy Methods in Amber18: Performance Enhancements and New Features. J. Chem. Inf. Model. 2018. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Lazaridis, T. The effect of water displacement on binding thermodynamics: Concanavalin A. J. Phys. Chem. B 2005, 109, 662–670. [Google Scholar] [CrossRef] [PubMed]
- Englert, L.; Biela, A.; Zayed, M.; Heine, A.; Hangauer, D.; Klebe, G. Displacement of disordered water molecules from hydrophobic pocket creates enthalpic signature: Binding of phosphonamidate to the S1′-pocket of thermolysin. BBA—Gen. Subj. 2010, 1800, 1192–1202. [Google Scholar] [CrossRef]
- Michel, J.; Tirado-Rives, J.; Jorgensen, W.L. Energetics of displacing water molecules from protein binding sites: Consequences for ligand optimization. J. Am. Chem. Soc. 2009, 131, 15403–15411. [Google Scholar] [CrossRef]
- García-Sosa, A.T.; Mancera, R.L.; Dean, P.M. WaterScore: A novel method for distinguishing between bound and displaceable water molecules in the crystal structure of the binding site of protein-ligand complexes. J. Mol. Model. 2003, 9, 172–182. [Google Scholar] [CrossRef]
- Crawford, T.D.; Tsui, V.; Flynn, E.M.; Wang, S.; Taylor, A.M.; Côté, A.; Audia, J.E.; Beresini, M.H.; Burdick, D.J.; Cummings, R.; et al. Diving into the Water: Inducible Binding Conformations for BRD4, TAF1(2), BRD9, and CECR2 Bromodomains. J. Med. Chem. 2016, 59, 5391–5402. [Google Scholar] [CrossRef]
- Ladbury, J.E. Just add water! The effect of water on the specificity of protein-ligand binding sites and its potential application to drug design. Chem. Biol. 1996, 3, 973–980. [Google Scholar] [CrossRef]
- Poornima, C.S.; Dean, P.M. Hydration in drug design. 1. Multiple hydrogen-bonding features of water molecules in mediating protein-ligand interactions. J. Comput. Aided Mol. Des. 1995, 9, 500–512. [Google Scholar] [CrossRef] [PubMed]
- Levinson, N.M.; Boxer, S.G. A conserved water-mediated hydrogen bond network defines bosutinib’s kinase selectivity. Nat. Chem. Biol. 2014, 10, 127–132. [Google Scholar] [CrossRef] [PubMed]
- García-Sosa, A.T. Hydration properties of ligands and drugs in protein binding sites: Tightly-bound, bridging water molecules and their effects and consequences on molecular design strategies. J. Chem. Inf. Model. 2013, 53, 1388–1405. [Google Scholar] [CrossRef] [PubMed]
- Sridhar, A.; Ross, G.A.; Biggin, P.C. Waterdock 2.0: Water placement prediction for Holo-structures with a pymol plugin. PLoS ONE 2017, 12, e0172743. [Google Scholar] [CrossRef] [PubMed]
- Bissantz, C.; Kuhn, B.; Stahl, M. A Medicinal Chemist’s Guide to Molecular Interactions. J. Med. Chem. 2010, 53, 5061–5084. [Google Scholar] [CrossRef] [PubMed]
- Wiesner, S.; Kurian, E.; Prendergast, F.G.; Halle, B. Water molecules in the binding cavity of intestinal fatty acid binding protein: Dynamic characterization by water 17O and 2H magnetic relaxation dispersion. J. Mol. Biol. 1999, 286, 233–246. [Google Scholar] [CrossRef] [PubMed]
- Gauto, D.F.; Di Lella, S.; Guardia, C.M.A.; Estrin, D.A.; Martí, M.A. Carbohydrate-binding proteins: Dissecting ligand structures through solvent environment occupancy. J. Phys. Chem. B 2009, 113, 8717–8724. [Google Scholar] [CrossRef] [PubMed]
- López, E.D.; Arcon, J.P.; Gauto, D.F.; Petruk, A.A.; Modenutti, C.P.; Dumas, V.G.; Marti, M.A.; Turjanski, A.G. WATCLUST: A tool for improving the design of drugs based on protein-water interactions. Bioinformatics 2015, 31, 3697–3699. [Google Scholar] [CrossRef] [PubMed]
- Klibanov, A.M. Improving enzymes by using them in organic solvents. Nature 2001, 409, 241–246. [Google Scholar] [CrossRef] [PubMed]
- Halling, P.J. What can we learn by studying enzymes in non-aqueous media? Philos. Trans. R. Soc. Lond. B Biol. Sci. 2004, 359, 1287–1296. [Google Scholar] [CrossRef] [PubMed]
- Allen, K.N.; Bellamacina, C.R.; Ding, X.; Jeffery, C.J.; Mattos, C.; Petsko, G.A.; Ringe, D. An Experimental Approach to Mapping the Binding Surfaces of Crystalline Proteins. J. Phys. Chem. 1996, 100, 2605–2611. [Google Scholar] [CrossRef]
- Liepinsh, E.; Otting, G. Organic solvents identify specific ligand binding sites on protein surfaces. Nat. Biotechnol. 1997, 15, 264–268. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- English, A.C.; Done, S.H.; Caves, L.S.; Groom, C.R.; Hubbard, R.E. Locating interaction sites on proteins: The crystal structure of thermolysin soaked in 2% to 100% isopropanol. Proteins 1999, 37, 628–640. [Google Scholar] [CrossRef] [Green Version]
- English, A.C.; Groom, C.R.; Hubbard, R.E. Experimental and computational mapping of the binding surface of a crystalline protein. Protein Eng. 2001, 14, 47–59. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Clackson, T.; Wells, J.A. A hot spot of binding energy in a hormone-receptor interface. Science 1995, 267, 383–386. [Google Scholar] [CrossRef] [PubMed]
- Caflisch, A. Computational combinatorial ligand design: Application to human alpha-thrombin. J. Comput. Aided Mol. Des. 1996, 10, 372–396. [Google Scholar] [CrossRef]
- Seco, J.; Luque, F.J.; Barril, X. Binding site detection and druggability index from first principles. J. Med. Chem. 2009, 52, 2363–2371. [Google Scholar] [CrossRef]
- Vukovic, S.; Huggins, D.J. Quantitative metrics for drug-target ligandability. Drug Discov. Today 2018, 23, 1258–1266. [Google Scholar] [CrossRef]
- Barril, X. Druggability predictions: Methods, limitations, and applications. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 327–338. [Google Scholar] [CrossRef]
- Guvench, O.; MacKerell, A.D., Jr. Computational fragment-based binding site identification by ligand competitive saturation. PLoS Comput. Biol. 2009, 5, e1000435. [Google Scholar] [CrossRef] [PubMed]
- Bakan, A.; Nevins, N.; Lakdawala, A.S.; Bahar, I. Druggability Assessment of Allosteric Proteins by Dynamics Simulations in the Presence of Probe Molecules. J. Chem. Theory Comput. 2012, 8, 2435–2447. [Google Scholar] [CrossRef] [PubMed]
- Ghanakota, P.; Carlson, H.A. Moving Beyond Active-Site Detection: MixMD Applied to Allosteric Systems. J. Phys. Chem. B 2016, 120, 8685–8695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sayyed-Ahmad, A.; Gorfe, A.A. Mixed-Probe Simulation and Probe-Derived Surface Topography Map Analysis for Ligand Binding Site Identification. J. Chem. Theory Comput. 2017, 13, 1851–1861. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; Lakkaraju, S.K.; Raman, E.P.; Fang, L.; MacKerell, A.D., Jr. Pharmacophore modeling using site-identification by ligand competitive saturation (SILCS) with multiple probe molecules. J. Chem. Inf. Model. 2015, 55, 407–420. [Google Scholar] [CrossRef] [PubMed]
- Ghanakota, P.; van Vlijmen, H.; Sherman, W.; Beuming, T. Large-Scale Validation of Mixed-Solvent Simulations to Assess Hotspots at Protein-Protein Interaction Interfaces. J. Chem. Inf. Model. 2018, 58, 784–793. [Google Scholar] [CrossRef] [PubMed]
- Alvarez-Garcia, D.; Barril, X. Molecular simulations with solvent competition quantify water displaceability and provide accurate interaction maps of protein binding sites. J. Med. Chem. 2014, 57, 8530–8539. [Google Scholar] [CrossRef]
- Graham, S.E.; Smith, R.D.; Carlson, H.A. Predicting Displaceable Water Sites Using Mixed-Solvent Molecular Dynamics. J. Chem. Inf. Model. 2018, 58, 305–314. [Google Scholar] [CrossRef]
- Uehara, S.; Tanaka, S. Cosolvent-Based Molecular Dynamics for Ensemble Docking: Practical Method for Generating Druggable Protein Conformations. J. Chem. Inf. Model. 2017, 57, 742–756. [Google Scholar] [CrossRef]
- Oleinikovas, V.; Saladino, G.; Cossins, B.P.; Gervasio, F.L. Understanding Cryptic Pocket Formation in Protein Targets by Enhanced Sampling Simulations. J. Am. Chem. Soc. 2016, 138, 14257–14263. [Google Scholar] [CrossRef]
- Comitani, F.; Gervasio, F.L. Exploring Cryptic Pockets Formation in Targets of Pharmaceutical Interest with SWISH. J. Chem. Theory Comput. 2018, 14, 3321–3331. [Google Scholar] [CrossRef] [PubMed]
- Kimura, S.R.; Hu, H.P.; Ruvinsky, A.M.; Sherman, W.; Favia, A.D. Deciphering Cryptic Binding Sites on Proteins by Mixed-Solvent Molecular Dynamics. J. Chem. Inf. Model. 2017, 57, 1388–1401. [Google Scholar] [CrossRef]
- Raman, E.P.; Yu, W.; Guvench, O.; Mackerell, A.D. Reproducing crystal binding modes of ligand functional groups using Site-Identification by Ligand Competitive Saturation (SILCS) simulations. J. Chem. Inf. Model. 2011, 51, 877–896. [Google Scholar] [CrossRef] [PubMed]
- Arcon, J.P.; Defelipe, L.A.; Modenutti, C.P.; López, E.D.; Alvarez-Garcia, D.; Barril, X.; Turjanski, A.G.; Martí, M.A. Molecular Dynamics in Mixed Solvents Reveals Protein-Ligand Interactions, Improves Docking, and Allows Accurate Binding Free Energy Predictions. J. Chem. Inf. Model. 2017, 57, 846–863. [Google Scholar] [CrossRef] [PubMed]
- Ghanakota, P.; Carlson, H.A. Driving Structure-Based Drug Discovery through Cosolvent Molecular Dynamics. J. Med. Chem. 2016, 59, 10383–10399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pan, A.C.; Borhani, D.W.; Dror, R.O.; Shaw, D.E. Molecular determinants of drug-receptor binding kinetics. Drug Discov. Today 2013, 18, 667–673. [Google Scholar] [CrossRef] [PubMed]
- Kuntz, I.D.; Chen, K.; Sharp, K.A.; Kollman, P.A. The maximal affinity of ligands. Proc. Natl. Acad. Sci. USA 1999, 96, 9997–10002. [Google Scholar] [CrossRef] [Green Version]
- Huang, D.; Caflisch, A. The free energy landscape of small molecule unbinding. PLoS Comput. Biol. 2011, 7, e1002002. [Google Scholar] [CrossRef]
- Lexa, K.W.; Goh, G.B.; Carlson, H.A. Parameter choice matters: Validating probe parameters for use in mixed-solvent simulations. J. Chem. Inf. Model. 2014, 54, 2190–2199. [Google Scholar] [CrossRef]
- Foster, T.J.; MacKerell, A.D., Jr.; Guvench, O. Balancing target flexibility and target denaturation in computational fragment-based inhibitor discovery. J. Comput. Chem. 2012, 33, 1880–1891. [Google Scholar] [CrossRef] [Green Version]
- Alvarez-Garcia, D.; Barril, X. Relationship between Protein Flexibility and Binding: Lessons for Structure-Based Drug Design. J. Chem. Theory Comput. 2014, 10, 2608–2614. [Google Scholar] [CrossRef] [PubMed]
- Erlanson, D.A.; Fesik, S.W.; Hubbard, R.E.; Jahnke, W.; Jhoti, H. Twenty years on: The impact of fragments on drug discovery. Nat. Rev. Drug Discov. 2016, 15, 605–619. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Shoichet, B.K. Molecular docking and ligand specificity in fragment-based inhibitor discovery. Nat. Chem. Biol. 2009, 5, 358–364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giannetti, A.M.; Shoichet, B.K. Docking for fragment inhibitors of AmpC β-lactamase. Proc. Natl. Acad. Sci. USA 2009, 106, 7455–7460. [Google Scholar]
- Zhao, H.; Gartenmann, L.; Dong, J.; Spiliotopoulos, D.; Caflisch, A. Discovery of BRD4 bromodomain inhibitors by fragment-based high-throughput docking. Bioorg. Med. Chem. Lett. 2014, 24, 2493–2496. [Google Scholar] [CrossRef] [PubMed]
- Spiliotopoulos, D.; Zhu, J.; Wamhoff, E.-C.; Deerain, N.; Marchand, J.-R.; Aretz, J.; Rademacher, C.; Caflisch, A. Virtual screen to NMR (VS2NMR): Discovery of fragment hits for the CBP bromodomain. Bioorg. Med. Chem. Lett. 2017, 27, 2472–2478. [Google Scholar] [CrossRef] [PubMed]
- Vass, M.; Agai-Csongor, E.; Horti, F.; Keserű, G.M. Multiple fragment docking and linking in primary and secondary pockets of dopamine receptors. ACS Med. Chem. Lett. 2014, 5, 1010–1014. [Google Scholar] [CrossRef]
- Marchand, J.-R.; Dalle Vedove, A.; Lolli, G.; Caflisch, A. Discovery of Inhibitors of Four Bromodomains by Fragment-Anchored Ligand Docking. J. Chem. Inf. Model. 2017, 57, 2584–2597. [Google Scholar] [CrossRef]
- Jubb, H.; Blundell, T.L.; Ascher, D.B. Flexibility and small pockets at protein-protein interfaces: New insights into druggability. Prog. Biophys. Mol. Biol. 2015, 119, 2–9. [Google Scholar] [CrossRef]
- Chipot, C.; Pohorille, A. Free Energy Calculations: Theory and Applications in Chemistry and Biology; Springer Science & Business Media: Berlin, Germany, 2007; ISBN 9783540384472. [Google Scholar]
- Chen, D.; Ranganathan, A.; IJzerman, A.P.; Siegal, G.; Carlsson, J. Complementarity between in silico and biophysical screening approaches in fragment-based lead discovery against the A(2A) adenosine receptor. J. Chem. Inf. Model. 2013, 53, 2701–2714. [Google Scholar] [CrossRef]
- Steinbrecher, T.B.; Dahlgren, M.; Cappel, D.; Lin, T.; Wang, L.; Krilov, G.; Abel, R.; Friesner, R.; Sherman, W. Accurate Binding Free Energy Predictions in Fragment Optimization. J. Chem. Inf. Model. 2015, 55, 2411–2420. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Roux, B. Free Energy Perturbation Hamiltonian Replica-Exchange Molecular Dynamics (FEP/H-REMD) for Absolute Ligand Binding Free Energy Calculations. J. Chem. Theory Comput. 2010, 6, 2559–2565. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Aldeghi, M.; Heifetz, A.; Bodkin, M.J.; Knapp, S.; Biggin, P.C. Accurate calculation of the absolute free energy of binding for drug molecules. Chem. Sci. 2016, 7, 207–218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, Y.-L.; Meng, Y.; Jiang, W.; Roux, B. Explaining why Gleevec is a specific and potent inhibitor of Abl kinase. Proc. Natl. Acad. Sci. USA 2013, 110, 1664–1669. [Google Scholar] [CrossRef] [PubMed]
- Dror, R.O.; Pan, A.C.; Arlow, D.H.; Borhani, D.W.; Maragakis, P.; Shan, Y.; Xu, H.; Shaw, D.E. Pathway and mechanism of drug binding to G-protein-coupled receptors. Proc. Natl. Acad. Sci. USA 2011, 108, 13118–13123. [Google Scholar] [CrossRef] [PubMed]
- Mondal, J.; Friesner, R.A.; Berne, B.J. Role of Desolvation in Thermodynamics and Kinetics of Ligand Binding to a Kinase. J. Chem. Theory Comput. 2014, 10, 5696–5705. [Google Scholar] [CrossRef] [PubMed]
- Tiwary, P.; Mondal, J.; Berne, B.J. How and when does an anticancer drug leave its binding site? Sci. Adv. 2017, 3, e1700014. [Google Scholar] [CrossRef] [PubMed]
- Lotz, S.D.; Dickson, A. Unbiased Molecular Dynamics of 11 min Timescale Drug Unbinding Reveals Transition State Stabilizing Interactions. J. Am. Chem. Soc. 2018, 140, 618–628. [Google Scholar] [CrossRef] [PubMed]
- Plattner, N.; Noé, F. Protein conformational plasticity and complex ligand-binding kinetics explored by atomistic simulations and Markov models. Nat. Commun. 2015, 6, 7653. [Google Scholar] [CrossRef] [PubMed]
- Bisignano, P.; Doerr, S.; Harvey, M.J.; Favia, A.D.; Cavalli, A.; De Fabritiis, G. Kinetic characterization of fragment binding in AmpC β-lactamase by high-throughput molecular simulations. J. Chem. Inf. Model. 2014, 54, 362–366. [Google Scholar] [CrossRef]
- Ferruz, N.; Harvey, M.J.; Mestres, J.; De Fabritiis, G. Insights from Fragment Hit Binding Assays by Molecular Simulations. J. Chem. Inf. Model. 2015, 55, 2200–2205. [Google Scholar] [CrossRef] [PubMed]
- Buch, I.; Giorgino, T.; De Fabritiis, G. Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc. Natl. Acad. Sci. USA 2011, 108, 10184–10189. [Google Scholar] [CrossRef] [PubMed]
- Rathi, P.C.; Ludlow, R.F.; Hall, R.J.; Murray, C.W.; Mortenson, P.N.; Verdonk, M.L. Predicting “Hot” and “Warm” Spots for Fragment Binding. J. Med. Chem. 2017, 60, 4036–4046. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Rosell, G.; Harvey, M.J.; De Fabritiis, G. Molecular-Simulation-Driven Fragment Screening for the Discovery of New CXCL12 Inhibitors. J. Chem. Inf. Model. 2018, 58, 683–691. [Google Scholar] [CrossRef] [PubMed]
- Ludlow, R.F.; Verdonk, M.L.; Saini, H.K.; Tickle, I.J.; Jhoti, H. Detection of secondary binding sites in proteins using fragment screening. Proc. Natl. Acad. Sci. USA 2015, 112, 15910–15915. [Google Scholar] [CrossRef] [PubMed]
- Shan, Y.; Kim, E.T.; Eastwood, M.P.; Dror, R.O.; Seeliger, M.A.; Shaw, D.E. How does a drug molecule find its target binding site? J. Am. Chem. Soc. 2011, 133, 9181–9183. [Google Scholar] [CrossRef]
- Colizzi, F.; Perozzo, R.; Scapozza, L.; Recanatini, M.; Cavalli, A. Single-molecule pulling simulations can discern active from inactive enzyme inhibitors. J. Am. Chem. Soc. 2010, 132, 7361–7371. [Google Scholar] [CrossRef]
- Gioia, D.; Bertazzo, M.; Recanatini, M.; Masetti, M.; Cavalli, A. Dynamic Docking: A Paradigm Shift in Computational Drug Discovery. Molecules 2017, 22, 2029. [Google Scholar] [CrossRef]
- Casasnovas, R.; Limongelli, V.; Tiwary, P.; Carloni, P.; Parrinello, M. Unbinding Kinetics of a p38 MAP Kinase Type II Inhibitor from Metadynamics Simulations. J. Am. Chem. Soc. 2017, 139, 4780–4788. [Google Scholar] [CrossRef]
- Ruiz-Carmona, S.; Schmidtke, P.; Luque, F.J.; Baker, L.; Matassova, N.; Davis, B.; Roughley, S.; Murray, J.; Hubbard, R.; Barril, X. Dynamic undocking and the quasi-bound state as tools for drug discovery. Nat. Chem. 2017, 9, 201–206. [Google Scholar] [CrossRef]
- Morris, G.M.; Huey, R.; Lindstrom, W.; Sanner, M.F.; Belew, R.K.; Goodsell, D.S.; Olson, A.J. AutoDock4 and AutoDockTools4: Automated docking with selective receptor flexibility. J. Comput. Chem. 2009, 30, 2785–2791. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Forli, S.; Huey, R.; Pique, M.E.; Sanner, M.F.; Goodsell, D.S.; Olson, A.J. Computational protein-ligand docking and virtual drug screening with the AutoDock suite. Nat. Protoc. 2016, 11, 905–919. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Carmona, S.; Alvarez-Garcia, D.; Foloppe, N.; Garmendia-Doval, A.B.; Juhos, S.; Schmidtke, P.; Barril, X.; Hubbard, R.E.; Morley, S.D. rDock: A fast, versatile and open source program for docking ligands to proteins and nucleic acids. PLoS Comput. Biol. 2014, 10, e1003571. [Google Scholar] [CrossRef] [PubMed]
- Sousa, S.F.; Ribeiro, A.J.M.; Coimbra, J.T.S.; Neves, R.P.P.; Martins, S.A.; Moorthy, N.S.; Fernandes, P.A.; Ramos, M.J. Protein-Ligand Docking in the New Millennium—A Retrospective of 10 Years in the Field. Curr. Med. Chem. 2013, 20, 2296–2314. [Google Scholar] [CrossRef] [PubMed]
- Cleves, A.E.; Jain, A.N. Knowledge-guided docking: Accurate prospective prediction of bound configurations of novel ligands using Surflex-Dock. J. Comput. Aided Mol. Des. 2015, 29, 485–509. [Google Scholar] [CrossRef] [PubMed]
- Hu, B.; Lill, M.A. PharmDock: A pharmacophore-based docking program. J. Cheminform. 2014, 6, 14. [Google Scholar] [CrossRef] [PubMed]
- Perryman, A.L.; Santiago, D.N.; Forli, S.; Martins, D.S.; Olson, A.J. Virtual screening with AutoDock Vina and the common pharmacophore engine of a low diversity library of fragments and hits against the three allosteric sites of HIV integrase: Participation in the SAMPL4 protein-ligand binding challenge. J. Comput. Aided Mol. Des. 2014, 28, 429–441. [Google Scholar] [CrossRef]
- Friesner, R.A.; Banks, J.L.; Murphy, R.B.; Halgren, T.A.; Klicic, J.J.; Mainz, D.T.; Repasky, M.P.; Knoll, E.H.; Shelley, M.; Perry, J.K.; et al. Glide: A new approach for rapid, accurate docking and scoring. 1. Method and assessment of docking accuracy. J. Med. Chem. 2004, 47, 1739–1749. [Google Scholar] [CrossRef]
- Jones, G.; Willett, P.; Glen, R.C.; Leach, A.R.; Taylor, R. Development and validation of a genetic algorithm for flexible docking. J. Mol. Biol. 1997, 267, 727–748. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Corbeil, C.R.; Williams, C.I.; Labute, P. Variability in docking success rates due to dataset preparation. J. Comput. Aided Mol. Des. 2012, 26, 775–786. [Google Scholar] [CrossRef] [Green Version]
- Allen, W.J.; Balius, T.E.; Mukherjee, S.; Brozell, S.R.; Moustakas, D.T.; Lang, P.T.; Case, D.A.; Kuntz, I.D.; Rizzo, R.C. DOCK 6: Impact of new features and current docking performance. J. Comput. Chem. 2015, 36, 1132–1156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Coleman, R.G.; Carchia, M.; Sterling, T.; Irwin, J.J.; Shoichet, B.K. Ligand pose and orientational sampling in molecular docking. PLoS ONE 2013, 8, e75992. [Google Scholar] [CrossRef] [PubMed]
- Balius, T.E.; Fischer, M.; Stein, R.M.; Adler, T.B.; Nguyen, C.N.; Cruz, A.; Gilson, M.K.; Kurtzman, T.; Shoichet, B.K. Testing inhomogeneous solvation theory in structure-based ligand discovery. Proc. Natl. Acad. Sci. USA 2017, 114, E6839–E6846. [Google Scholar] [CrossRef] [PubMed]
- Uehara, S.; Tanaka, S. AutoDock-GIST: Incorporating Thermodynamics of Active-Site Water into Scoring Function for Accurate Protein-Ligand Docking. Molecules 2016, 21, 1604. [Google Scholar] [CrossRef] [PubMed]
- Gohlke, H.; Hendlich, M.; Klebe, G. Knowledge-based scoring function to predict protein-ligand interactions. J. Mol. Biol. 2000, 295, 337–356. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muegge, I.; Martin, Y.C. A general and fast scoring function for protein-ligand interactions: A simplified potential approach. J. Med. Chem. 1999, 42, 791–804. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Merz, K.M. Development of the Knowledge-Based and Empirical Combined Scoring Algorithm (KECSA) To Score Protein–Ligand Interactions. J. Chem. Inf. Model. 2013, 53, 1073–1083. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Wu, Y.; Deng, Y.; Kim, B.; Pierce, L.; Krilov, G.; Lupyan, D.; Robinson, S.; Dahlgren, M.K.; Greenwood, J.; et al. Accurate and reliable prediction of relative ligand binding potency in prospective drug discovery by way of a modern free-energy calculation protocol and force field. J. Am. Chem. Soc. 2015, 137, 2695–2703. [Google Scholar] [CrossRef]
- García-Sosa, A.T.; Mancera, R.L. Free Energy Calculations of Mutations Involving a Tightly Bound Water Molecule and Ligand Substitutions in a Ligand-Protein Complex. Mol. Inform. 2010, 29, 589–600. [Google Scholar] [CrossRef]
- Aldeghi, M.; Ross, G.A.; Bodkin, M.J.; Essex, J.W.; Knapp, S.; Biggin, P.C. Large-scale analysis of water stability in bromodomain binding pockets with grand canonical Monte Carlo. Commun. Chem. 2018, 1, 19. [Google Scholar] [CrossRef] [Green Version]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Defelipe, L.A.; Arcon, J.P.; Modenutti, C.P.; Marti, M.A.; Turjanski, A.G.; Barril, X. Solvents to Fragments to Drugs: MD Applications in Drug Design. Molecules 2018, 23, 3269. https://doi.org/10.3390/molecules23123269
Defelipe LA, Arcon JP, Modenutti CP, Marti MA, Turjanski AG, Barril X. Solvents to Fragments to Drugs: MD Applications in Drug Design. Molecules. 2018; 23(12):3269. https://doi.org/10.3390/molecules23123269
Chicago/Turabian StyleDefelipe, Lucas A., Juan Pablo Arcon, Carlos P. Modenutti, Marcelo A. Marti, Adrián G. Turjanski, and Xavier Barril. 2018. "Solvents to Fragments to Drugs: MD Applications in Drug Design" Molecules 23, no. 12: 3269. https://doi.org/10.3390/molecules23123269
APA StyleDefelipe, L. A., Arcon, J. P., Modenutti, C. P., Marti, M. A., Turjanski, A. G., & Barril, X. (2018). Solvents to Fragments to Drugs: MD Applications in Drug Design. Molecules, 23(12), 3269. https://doi.org/10.3390/molecules23123269